基于影响系数的高速公路行车风险评估模型

邱 磊，叱干都，邓志刚，刘建蓓,马小龙

(1.中交第一公路勘察设计研究院有限公司 交通安全应急保障技术交通运输行业研发中心，陕西 西安 710075；2.广东省路桥建设发展有限公司，广东 广州 510623)

0 引言

高速公路行车风险模型化描述方法可分为两类：一类是基于高速公路已有交通事故统计资料，从事故特征和发生规律评价高速公路行车风险，包括绝对事故数法、相对事故率法、回归分析法、交通冲突法、时间序列法、灰色评价法等，如德国道路与交通研究协会的《道路安全评价建议》[1]，通过事故数据，具体分析交通事故和道路安全性的关系，英国伦敦大学Smeed R.J.通过欧洲20多个国家的事故调查数据回归分析建立的斯密德模型[2]，王洪波[3]通过事故数据对交通事故成因与交通设施安全的关系与影响进行分析，孙小端[4]等根据事故数据研究了车速离散性和事故率等关系[4]，这类方法基于事故统计资料，依据翔实可靠，但其建立需要大量的事故积累，所需收集的信息量庞大，在高速公路交通安全决策中难于应用。另一类是通过分析高速公路交通安全风险的主要影响因素，提取安全评价指标建立数学模型评价行车风险，包括层次分析法、灰色聚类模型、熵权物元模型、神经网络评价模型、主客观综合评价模型等。如美国联邦公路局的“交互式公路安全设计模型(IHSDM)”，从车辆动态、车速一致性、事故预计、道路设施、驾驶心理等人车路不同方面信息评价道路安全性[5]，交通运输部颁布的《公路项目安全性评价规范》(JTGB05—2005)(以下简称《规范》)，针对公路项目建设的不同阶段，从运行速度协调性、路线、路侧、隧道、交叉、交通工程及沿线设施等不同方面对公路的安全性进行评价，但主要以运行速度评价为核心[6]。陈杰[7]建立的兼顾主客观因素的高速公路交通安全综合评价模型，分别构建基于层次熵和基于向量相似度的综合评价模型。孟祥海对“同质性路段”分别建立了4种负二项回归模型,通过精度评价指标选择出最优的事故预测模型[8]。周宏敏等融合设计经验，对《公路项目安全性评价指南》运行速度预测与协调性评价模型进行修正[9]。杨春风等从道路线形、路面状况、安全设施和交通环境等4个方面构建了以公路安全等级评价为目标的公路安全评价二级指标体系[10]。薛墒从平面线形、纵断面线形、平纵线形组合以及视距等4个方面分析了公路几何线形与公路运行安全之间的关系[11]。这一类方法更倾向于数学模型的构建，所需收集信息较少，但这类方法在应用中面临多个评价指标聚合问题，指标聚合的过程中往往通过经验判断各指标的聚合权重，带有一定的主观任意性。为修正以往高速公路行车风险评估方法，去除评价方法的主观性，首先分析高速公路不同行驶状态下的风险，获得风险函数及风险评价指标，确定各指标代表值，给予指标代表值一定比例增量，利用风险函数计算风险增量，根据风险增量的大小确定对应指标权重，根据加法原则将不同指标进行聚合，从而建立更为客观的高速公路不同行驶状态的行车风险评估模型。

1 高速公路行车风险分析

高速公路车辆的行驶状态可划分为3种：自由行驶状态、换车道行驶状态、跟车行驶状态[12]。3种行驶状态下均需满足车辆行驶稳定条件，换车道和跟车行驶状态需满足各自状态碰撞安全限制条件。

1.1 车辆行驶稳定性分析

车辆行驶稳定性包括横向倾覆稳定性、横向滑移稳定性和纵向稳定性，其中，横向倾覆和纵向稳定性可以通过限制高速公路最大纵坡、优化车辆重心高度和提高限载规定进行改善，而对自由行驶状态车辆稳定性产生影响的主要是横向滑移稳定性。横向滑移稳定条件为：

(1)

式中，v为车速；g为重力加速度；k为道路平面曲率；ic为道路横坡度；μc为路面横向摩擦系数。

将公式(1)进行移项处理，定义风险函数为：

(2)

该函数值小于0时车辆发生失稳，而大于0时，其函数值越小，说明其发生失稳的风险越大。

1.2 换车道行驶车辆碰撞风险分析

换车道行驶需要满足3个碰撞安全限制条件[13]：

(1)驶离原车道前与原车道前车保持安全距离；

(2)进入新车道时不与新车道空隙后车发生侧碰或者追尾；

(3)进入新车道后不与新车道的前车发生追尾。

假设换车道过程中车辆在两个车道行驶时间相等，这3个条件可以用公式表达为：

(3)

(4)

(5)

式中，v1，v2，v3，v4分别为原车道前车、换车道车辆、目标车道前车、目标车道后车的车速；a为换车道车辆加速度；Δt为车辆换车道所用时间；L为车辆安全车距；ΔSi_j为车辆i和j之间的车头空距。

公式(3)～(5)中都包含车头空距、车速差与换车道时间乘积、加速度与换车道时间平方的乘积、安全车距。既然每个公式表达的都是这些变量之间的相关关系，那么这些公式中至少有1个公式对它们的关系表达得更为严格，这些公式就可以最终被这个公式所代表，即该公式的限制范围必然是这些公式的交集。

我们可以得到最终的限制条件为：

(6)

假设车辆进入目标车道所做的运动为匀减速运动，匀减速车辆的减速时间为：

那么车辆减速度为：

同时，根据交通密度的特性，车头空距ΔS与交通密度K之间有着如下的关系：

ΔS=1 000/K。

而交通密度又与交通量和车速之间有着这样的关系：

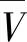
另外，对于车速差Δv，一般用85%位车速与15%位车速之差来反映[14]，我们引入车速波幅Av，并定义：

Av=v85-v15，

则换车道行驶状态下的碰撞风险函数可定义为：

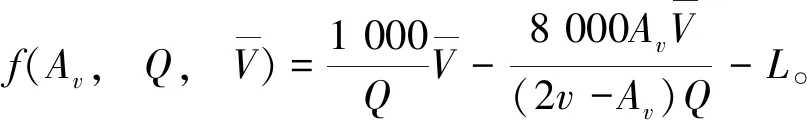
(7)

1.3 跟车行驶车辆碰撞风险分析

跟车行驶状态车辆的碰撞风险限制条件为[15]:

(8)

根据交通流特性对公式(8)进行变形后，跟车行驶状态下的碰撞风险函数可定义为：

f(il,v,Av,Q,μl)=

(9)

式中，v为车速；Δv为前后车速度差；il为道路纵坡度；μl为路面纵向摩擦系数；τ为反应时间。其余参数意义同公式(7)。

经过这一节的分析，对高速公路行车风险产生影响的主要因素包括3类：第1类为道路设计指标，包括道路平面曲率、路面横坡、路面纵坡；第2类为车流运行指标，包括运行车速、车速波幅、交通量；第3类为路面性能指标，包括路面摩擦系数。将这7个因素作为高速公路行车风险评估指标。

2 模型评估指标

2.1 指标标准化处理

采用无量纲化处理评价指标[16]，常用的无量纲化方法中，效用系数法在处理中满足了无量纲化处理的单调性、差异不变性、可平移性等基本属性，同时还修正了极差变换法所得结果受个别极值影响较大的特性，保证了评价方法结构的稳定性[17]，因此选择效用系数法对指标进行标准化处理。

效用系数法的基本表达式为：

(10)

式中，xi为标准化处理之前的值；αi为标准化处理后的值；a，b为常数；xm，xn为可以容许的最大值和最小值。

2.2 道路平面曲率

道路平面曲率主要对行驶车辆的横向滑移稳定性产生影响。对于平面曲率的允许值，不同的高速公路在不同的地形条件下的取值范围较广，小半径曲线在整条高速公路中所占的比例不尽相同，而正是这一点会对模型结果的稳定性产生影响，我们选取85%位曲率作为平面曲率的最大允许值，以保证模型的稳定性。

在统计学中，工程中的许多事物在实际情况中符合铃型曲线，在距离平均值小于一个标准差内的数据占全部数据的68.3%，而小于平均值加一个标准差的数据占全部数据的84.2%，因此提出85%位曲率的概念。

定义85%位曲率为：对于横轴(X轴)为桩号(取整个评价路段)，纵轴(Y轴)为平面曲率的平面曲率图，如一条平行于X轴的直线与平面曲率曲线及X轴三者所围成的面积正好等于平面曲率曲线与X轴所围成面积的85%，那么这条直线在Y轴上的截距即为85%位曲率(k85)。

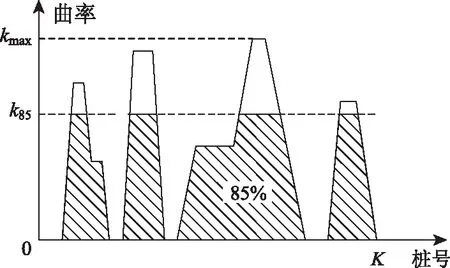
图1 85%位曲率示意图Fig.1 Schematic diagram of 85% bitwise curvature

2.3 路面横坡

路面横坡主要对行驶车辆的横向滑移稳定性产生影响，同道路平面曲率，选取85%位路面横坡作为路面横坡的最大容许值，最小容许值为0。

2.4 路面纵坡

路面纵坡会影响到驾驶员对于车辆速度的控制，从而影响车辆跟车距离，影响跟车行驶车辆的安全性。同道路平面曲率，选取85%位路面纵坡作为路面纵坡的最大容许值，最小容许值为0。

2.5 运行车速

车速是反映车辆稳定性和车辆事故严重程度的重要指标，采用交通工程中的85%位车速和15%位车速作为容许值范围。

2.6 车速波幅

车速波幅是反映车辆运行稳定性和事故严重程度的重要指标，根据已有成果，其容许值为0～30 km/h；

2.7 交通量

交通量是影响跟车行驶和换车道行驶安全性的重要指标，仅限定其最大容许值，根据交通工程中的规定，以服务保证率高达99.7%的设计小时交通量Q30作为其最大容许值。

2.8 路面摩擦系数

路面摩擦系数是反映车辆的稳定性和跟车行驶安全性的重要指标，对于路面摩擦系数，通过《公路沥青路面养护技术规范》(JTJ073.2—2001)[18]和实测统计获得容许值。

7个评估指标的容许值如表1所示。

表1 评估指标容许值Tab.1 Permissible value of assessment indicators

3 指标权重

设道路平面曲率、路面横坡、路面纵坡、运行车速、车速波幅、交通量和路面摩擦系数的权重系数分别为β1，β2，β3，β4，β5，β6，β7。分别计算不同车辆行驶状态下的风险指标聚合权重。

3.1 自由行驶状态

引入影响系数的概念确定每个指标对于风险的影响程度，以公式(2)为例，保持公式中的其它因素不变，给某个指标代表值10%的增量，通过各指标的代表值，获得风险函数的增量Δf，通过Δf的大小确定该指标的权重，因为此方法是基于“影响程度”确定聚合权重，因此称这种方法为影响系数法。

针对不同指标的风险增量计算公式如下：

(11)

Δf2=Δic，

(12)

(13)

Δf6=Δμc。

(14)

总的风险增加值计算公式为：

(15)

各指标对风险函数值影响程度即权重，计算公式为：

(16)

3.2 换车道行驶状态

仿照自由行驶状态下的计算方法，换车道行驶状态下，针对不同指标的风险增量计算公式如下：

(17)

(18)

(19)

总风险增加值及权重计算式为式(15)和(16)。

3.3 跟车行驶状态

跟车行驶状态下，针对不同指标的风险增量计算公式如下：

(20)

(21)

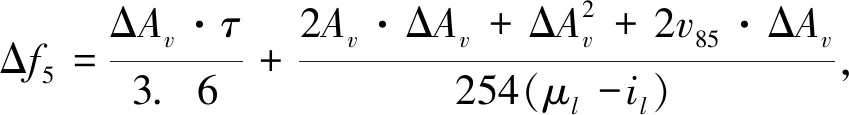
(22)

(23)

(24)

最后，将不同车辆行驶状态下的指标权重计算公式汇总如表2所示。

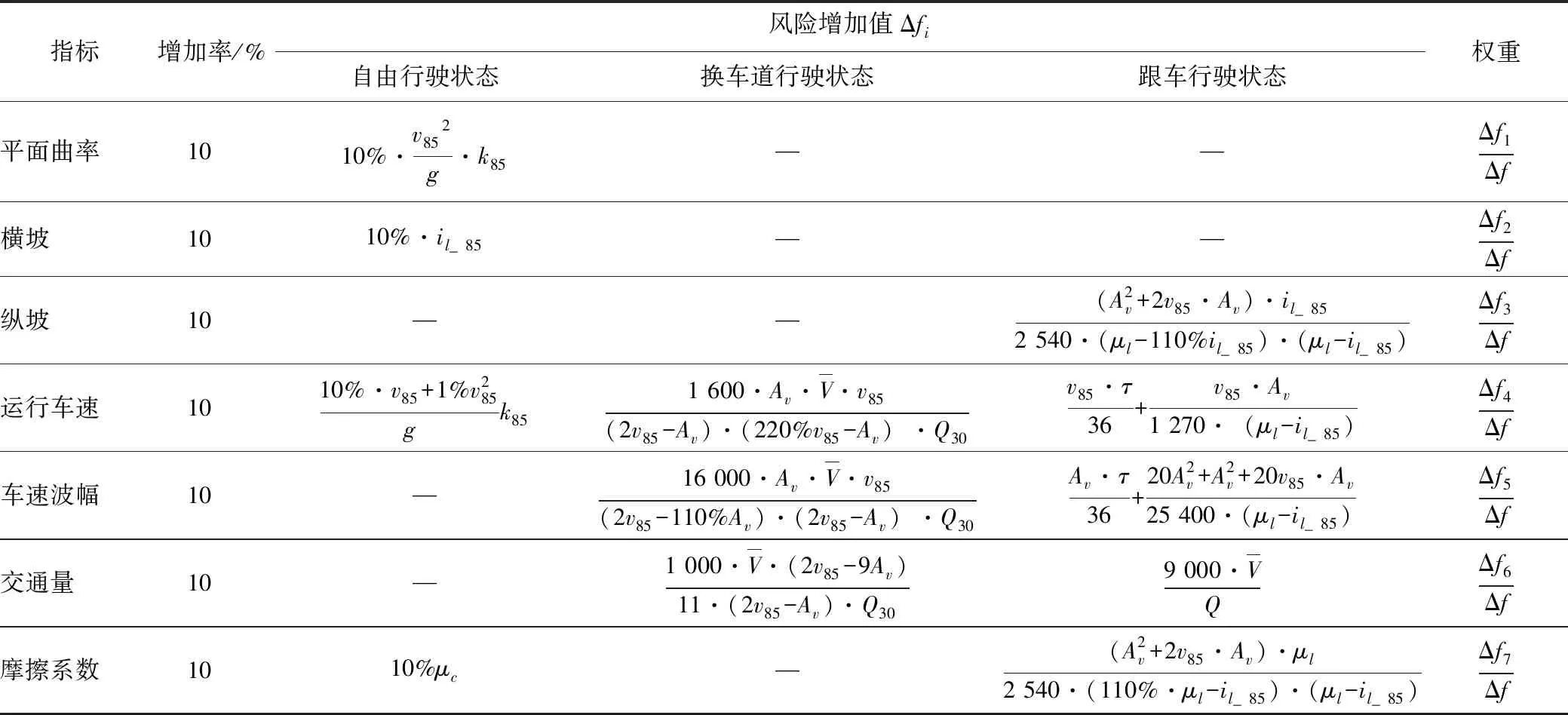
表2 不同行驶状态下指标权重计算汇总Tab.2 Summary of calculating indicator weights in different driving states

4 模型建立

经过上一节中各指标权重的确定，可以获得不同行驶状态的风险值模型的数学表达式为：

(25)

式中，f1为车辆自由行驶状态的行车风险；f2换车道行驶状态的行车风险；f3为跟车行驶状态的行车风险。通过对不同的指标进行分级后，计算了19 200种不同的指标组合情况，根据风险值的分布情况，给出了高速公路行车风险等级划分标准。

表3 风险等级划分标准Tab.3 Risk level classification criterion

5 模型验证

为了验证模型的准确性，以陕西省定汉线宝鸡至坪坎高速公路(YK135+682.129～YK191+074.366)基本数据为基础，运用模型进行风险评价，图2中绘出了路段的曲率半径和纵坡随桩号的变化曲线，经过计算该路段的85%位曲率半径为394.49 m，85%位纵坡值为0.078 9，在图2中用虚线表示。路段的运行车速和车速差如图3所示。路段限速值为80 km/h，路段运行速度为100.04 km/h。新建高速公路横向力系数按照《公路沥青路面养护技术规范》中的规定应不小于40，因此统一按照0.4取值。

图2 陕西定汉线宝鸡至坪坎公路曲线半径及纵坡度Fig.2 Curve radius and longitudinal gradient of Baoji-Pingkan highway on Dingbian-Hanzhong line in Shaanxi Province

经计算，该路段车辆在自由行驶、换车道行驶、跟车行驶不同状态下的风险如图4所示，从中可以筛选出不同状态下的高风险路段，换车道行驶的较高风险路段K174+874-K176+621与《规范》给出的应禁止变换车道路段吻合，跟车行驶的较高风险路段K174+874-K178+426和K177+562-K179+023与《规范》给出的设置车速确认标志的路段相吻合，路段基本信息和风险较高路段筛选结果见表4。

图3 陕西定汉线宝鸡至坪坎公路运行车速及速度波幅Fig.3 Vehicle speed and velocity wave amplitude of Baoji-Pingkan highway on Dingbian-Hanzhong line in Shaanxi Province

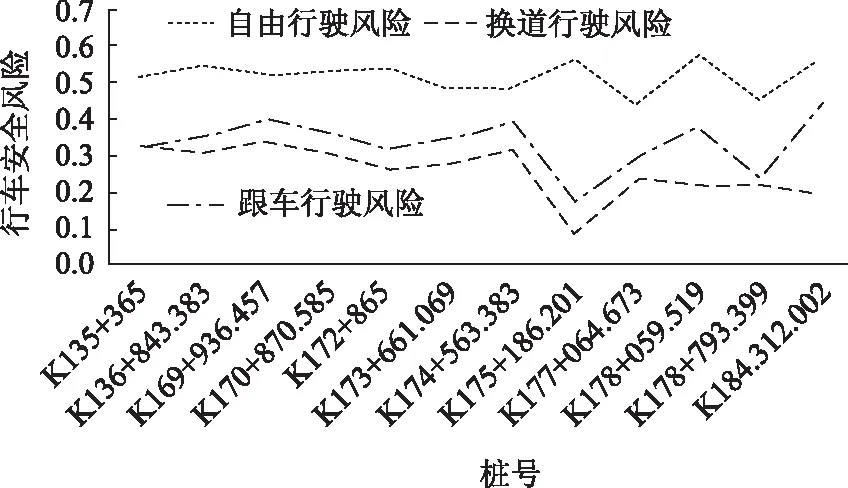
图4 陕西定汉线宝鸡至坪坎公路分状态行车安全风险图Fig.4 Curves of traffic safety risks by state of Baoji-Pingkan Highway on Dinghan Line in Shaanxi Province

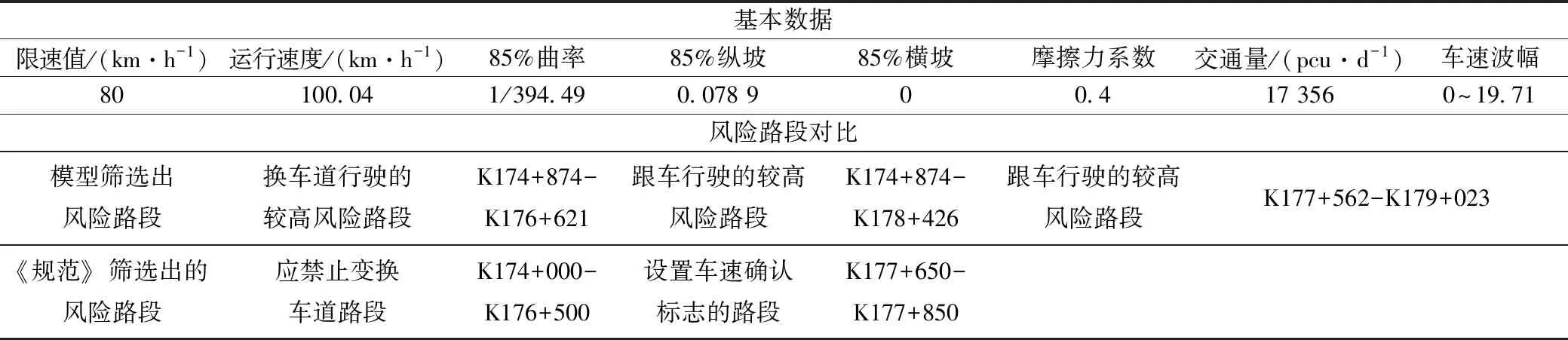
表4 实例验证Tab.4 Example verification

在模型验证中，自由行驶风险受平面曲率影响较大，因为在自由行驶过程中，车辆的主要受道路线形限制，而平面曲线是影响自由行驶的主要因素。换车道行驶受车速波幅和交通量的影响较大，因为换车道行驶过程中交通量是影响车辆侧向安全的主要因素，而车速差是导致车辆间碰撞的主要原因。跟车行驶受车速波幅的影响较大，因为跟车行驶中车速差距是导致车辆碰撞事故的主要原因。模型体现出的主要影响因素与实际情况相符。

6 结论

(1)用影响系数法确定了高速公路行车风险评估指标聚合权重计算方法，解决了权重确定的主观任意性，评估模型筛选出的危险路段准确性较高。

(2)通过实例验证，模型与《规范》筛选出的风险路段一致，模型对于风险的辨识度较好，同时对《规范》中的评价方法从车辆、道路、环境等方面进行了更为全面的优化和完善。

(3)模型的一致性较好，但单一因素对总风险值的影响较大，其稳定性尚需进一步的调整和修正。