随机事件概率的解题思路与方法

钟生秀

(福建省三明市第二中学 365000)

一、概率与代数融合

概率问题经常会与函数、方程等结合出现，即将统计概率的某些知识和数或代数相结合，或者是基于函数的图象性质来考察目标点落在函数图象上的概率.

例1如图1所示，桌面上摆放有三张不透明的相同卡片，三张卡片正面分别写着-1、-2、3，将三张卡片洗匀后扣在桌面上，分两次从上述三张卡片中随机抽取一张，第一次抽取卡片得到的数字记作函数y=kx+b中k的取值，第二次余下的两张卡片中抽取一张记作函数y=kx+b中b的取值.

(1)求函数y=kx+b中k的取值为负的概率；

(2)求函数y=kx+b图象经过第二、三、四象限的概率(用图表或列表法求解).

图1

分析从题目可知，抽中三个卡片为随机事件，且抽中-1、-2、3的可能均等，共三种结果，k为负值的可能性为两种.因此，可直接求得函数y=kx+b中k的取值为负的概率为2/3.当函数y=kx+b经过第二、三、四象限时则表明函数中k<0,b<0，而根据题目可知共有六个函数情况.而可求出函数y=kx+b中k<0,b<0的情况如表1所示.

第一次抽取第二次抽取-1-23-1(-1,-2)(-1,3)-2(-2,-1)(-2,3)3(3,-1)(3,-2)

解答(1)P(函数y=kx+b中k的取值为负)=2/3.(2)P(函数y=kx+b图象经过第二、三、四象限)=2/6=1/3.

总结：本题较为简单，考查学生对随机事件可能性的分析，可直接利用概率公式对题目进行解答，同时，题目还结合函数基本知识，对学生掌握基本知识的情况进行考查.

二、概率与图形面积

概率与图形知识的结合，往往用一个点落在某一几何图形内的可能性来表示，而几何面积的变化影响了点落在目标几何图形内的概率，这种类型的题目往往是空间与图形的契合，是数形结合的表现.

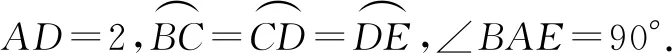
分析求点P落在四边形ABCD区域内的概率，则首先需要求出四边形ABCD的面积，而(1)中求解的为△CAD的面积，故只需计算出△ABC的面积即可.

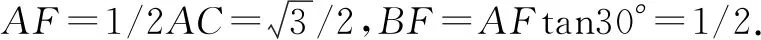
三、概率定义解题

例3桌面上摆放有7张大小相同的卡片，卡片分别标有2、3、4、5、6、7、8数字，随机从上述7张卡片中抽出两张，并组成一个分数，求组成分数为最简分数的概率____.

总结：题目中所包含的结果共有21种，在对本题进行求解时无需将全部结果一一列出，可利用互斥事件的概率和为1进行求解，对求解过程进行简化.

四、使用概率模型

在对随机事件概率进行求解的过程中，可以利用古典概型以及几何概型进行归纳，之后借助概型计算方法

进行求解.

例4假设一不透明口袋内装有7个苹果与3个梨子，这些苹果、梨子的大小一致，如果从口袋内随机拿出两个水果，问取出的两个水果一个为苹果，另一个为梨子的概率是多少.

在使用古典概率模型进行求解前，首先需要查看实验是否满足古典概率模型基本条件，若满足古典概率模型使用条件则可直接利用排列组合知识进行求解.