基于粒子群优化的深度随机神经网络

凌青华,宋余庆,韩 飞

(1.江苏大学 计算机科学与通信工程学院, 镇江 212013) (2.江苏科技大学 计算机学院, 镇江 212003)

超限学习机(extreme learning machine,ELM)[1]为单隐层前馈随机神经网络的一类有效学习算法．该算法随机选择输入层权值和隐单元阈值,并通过摩尔-彭若斯广义逆解析，确定网络输出层权值．相对于传统的神经网络梯度学习算法,超限学习机能够以极快的速度获得更优的泛化性能;同时,超限学习机中隐单元激活函数不需要一定可微,在学习过程中不用考虑停止规则、学习率和迭代次数等问题．相对于支持向量机，超限学习机仅需确定隐层节点数,不需要进行复杂的参数选择,在多类别分类问题和回归问题上均能获得良好性能．因此,近十年来,ELM在生物医学数据分析,农业病虫害预测、卫星遥感图像处理等领域得到了广泛应用[2]．

深度学习是包含多个隐层的深度网络结构下的机器学习算法,其动机在于建立模拟人脑分析学习的神经网络.它模仿人脑机制来解释数据，实现对信息进行分级处理,由低级特征组合形成高级特征,特征表达逐渐抽象化．深度模型通过堆叠网络的层数来逐层表达输入数据的不同级别特征,网络结构内部每层的输出都作为其下一层的输入,从而更好地学习原始数据的内在联系．深度自动编码器是深度学习的一种常用模型,是一种尽可能复现输入数据特征的学习过程[3],但其训练过程太长,时间开销过大．为了克服传统深度自动编码器时间开销过大的缺陷,文献[4]中提出了基于随机自动编码器的深度随机神经网络模型——多层超限学习机(multi layer-ELM,ML-ELM)，实现逐层学习,实现了较优的泛化性能,且时间开销远低于传统深度结构网络．

多层超限学习机中初始权值随机确定,而随机确定的权值最终决定着各层的连接权值．因此,初始随机权值影响着多层超限学习机的性能,会导致多层超限学习机的性能不稳定．为了降低初始权值设置的盲目性,文中一方面将利用粒子群优化算法(particle swam optimization,PSO)，结合网络的输入输出灵敏度信息对各随机自动编码器初始权值进行优选,尽可能选出最优的各层随机自动编码器的初始权值,从而提高多层随机网络的稳定性;另一方面,对整个多层网络所获取的各层权值利用PSO作进一步全局优化,以建立最优的全局网络结构．实验表明,相对于传统的深度神经网络,文中提出的方法能够大大降低特征降维的时间开销;而相对于传统的随机深度神经网络,虽然在时间开销上略有增加,但能获取更关键、有效的特征,从而有利于获得更优的分类预测性能．

1 深度随机神经网络

1.1 随机自动编码器

随机神经网络可以看成是将数据的输入特征表示成不同的形式,分为特征压缩、特征稀疏表示和等维变换等．单隐层前馈随机神经网络中连接输入节点和隐节点的权值随机产生,从而将输入数据映射到另一随机特征空间．在随机神经网络自动编码器中,网络的输出等同于网络的输入．

不妨假设单隐层前馈神经网络中隐层节点数为L,则随机网络的输出:

(1)

式中：β为输出层权值矩阵；h(X)=[g1(X),g2(X),…,gL(X)]为输入向量X的隐层输出,即随机隐层特征．由于在自动编码器中输出向量就是输入向量,从而有:

Hβ=X

(2)

随机神经网络输出层权值 通过最小二范数均方差计算，其中H+为隐层输出矩阵摩尔·彭若斯(moore-penrose,MP)广义逆:

β=H+X

(3)

为了改进网络的泛化性能,在式(3)中增加正则项来提高解的鲁棒性．

(4)

以上网络训练与超限学习机一致,故称之为超限学习机自动编码器(ELM-auto encoder,ELM-AE)．相对于传统的神经网络自动编码器,ELM-AE能够极快地训练出泛化性能良好的网络．

奇异值分解(singular value decomposition,SVD)是一类常见的特征表达方法．文献[4]中ELM-AE采用类似于奇异值分解的方法进行特征表达．式(4)的奇异值分解为:

(5)

式中：ui为HHT的特征向量；di为H的特征值，N为样本数.

1.2 粒子群优化算法

文献[5]对Hepper的模拟鸟群(鱼群)模型进行修正，提出粒子群优化算法．PSO是一类基于群体搜索的随机优化方法,其中每个个体称为粒子,群体由所有个体组成,称为种群．每个粒子代表优化问题的一个可能解．

在PSO优化过程中,每个粒子在多维搜索空间飞行,根据自己的个体经验和近邻粒子的群体经验调整自己在搜索空间的位置．因此,每个粒子利用自身飞过的最佳位置,即个体历史最优Pbest和其邻居粒子中最优粒子,即全局最优粒子Gbest的信息来调整自己的飞行方向．

每个粒子的优劣,即其离真正全局最优解的距离，由一个预先定义的适应度函数来评价,该适应度函数与具体要解决的问题相关．

不妨假设第i个粒子在第t个时间步长的位置为xi(t),粒子的位置更新通过在原有位置向量上增加速度向量来改变,如式(6、7)[6]．

Xi(t+1)=Xi(t)+Vi(t+1)

(6)

Vij(t+1)=wVij(t)+c1r1j(t)(Pbj(t)-Xij(t))+

c2r2j(t)(Pgj(t)-Xij(t))

(7)

式中：w为惯性权重,对算法的收敛起到了重要的作用,并能有效平衡种群的探测与开发能力;Pbj(t)为第i个粒子的个体最优位置对应的分量;Pgj(t)为种群全局最优粒子对应的分量．

1.3 随机前馈网络的输入输出灵敏度

神经网络的输入输出灵敏度反应网络的输出对输入变化的敏感程度．较低的网络输入输出灵敏度使得网络具有较好的鲁棒性,从而提高网络的泛化性能[7]．

考虑一个含有L-1个隐层的前馈神经网络,yi对应于xk的输入输出灵敏度为:

(8)

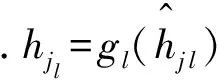
在超限学习机中,网络为单隐层前馈神经网络,输出层为线性单元,yi对应于xk在第l个样本上的输入输出灵敏度为:

(9)

因此,在所有样本上的输入输出灵敏度可以用下式计算:

(10)

式中：n,m和N分别为输入单元数目、输出单元数目和训练样本数目．为了更准确地获取网络的灵敏度值,在实际实验中根据式(10)重复计算多次取均值．

2 基于粒子群优化的多层随机前馈神经网络(PSO-ML-ELM)

相对于传统的深度学习网络,多层随机前馈神经网络ML-ELM[4]前向快速训练网络各层的权值,且不反向微调,从而大大减少多层网络的训练时间;同时由于ELM采用最小范数最小均方差方法获取网络的各层权值,ML-ELM泛化性能优于传统深度学习网络．ML-ELM结构如图1.

然而,ML-ELM在依次训练各隐层时,隐层权值为对应的随机网络自动编码器输出层权值．当随机网络自动编码器的输入层权值确定后,就可以通过MP广义逆唯一确定．因此,ML-ELM各隐层的网络权值由相应的随机网络自动编码器的输入层权值决定．而在ML-ELM中,所有随机网络自动编码器的输入层权值均为随机设置,不合适的随机输入层权值会导致较差的输出层权值,且较大可能使得自动编码器条件性能降低,使得ML-ELM中隐层结构不合理,最终影响ML-ELM的性能．

传统的多层随机神经网络ML-ELM虽然能大大提高训练速度、大幅度减少时间,但由于随机设置随机神经网络自动编码器输入层权值,导致ML-ELM性能不够稳定,且有一定的改进空间．文中将采用PSO对各ELM-AE中输入层权值进行优选以期得到最优的各隐层权值,从而提高多层随机神经网络的泛化性能．该算法将PSO用于优化ML-ELM,故称为PSO-ML-ELM,其算法流程图如图2．

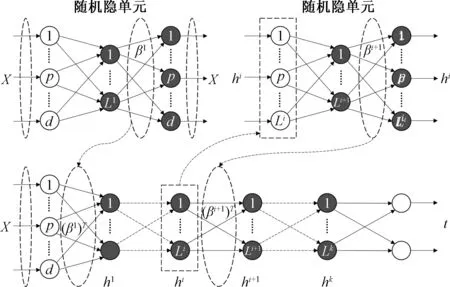
图1 多层随机神经网络(ML-ELM)结构Fig.1 Frame of multi layer random neural network

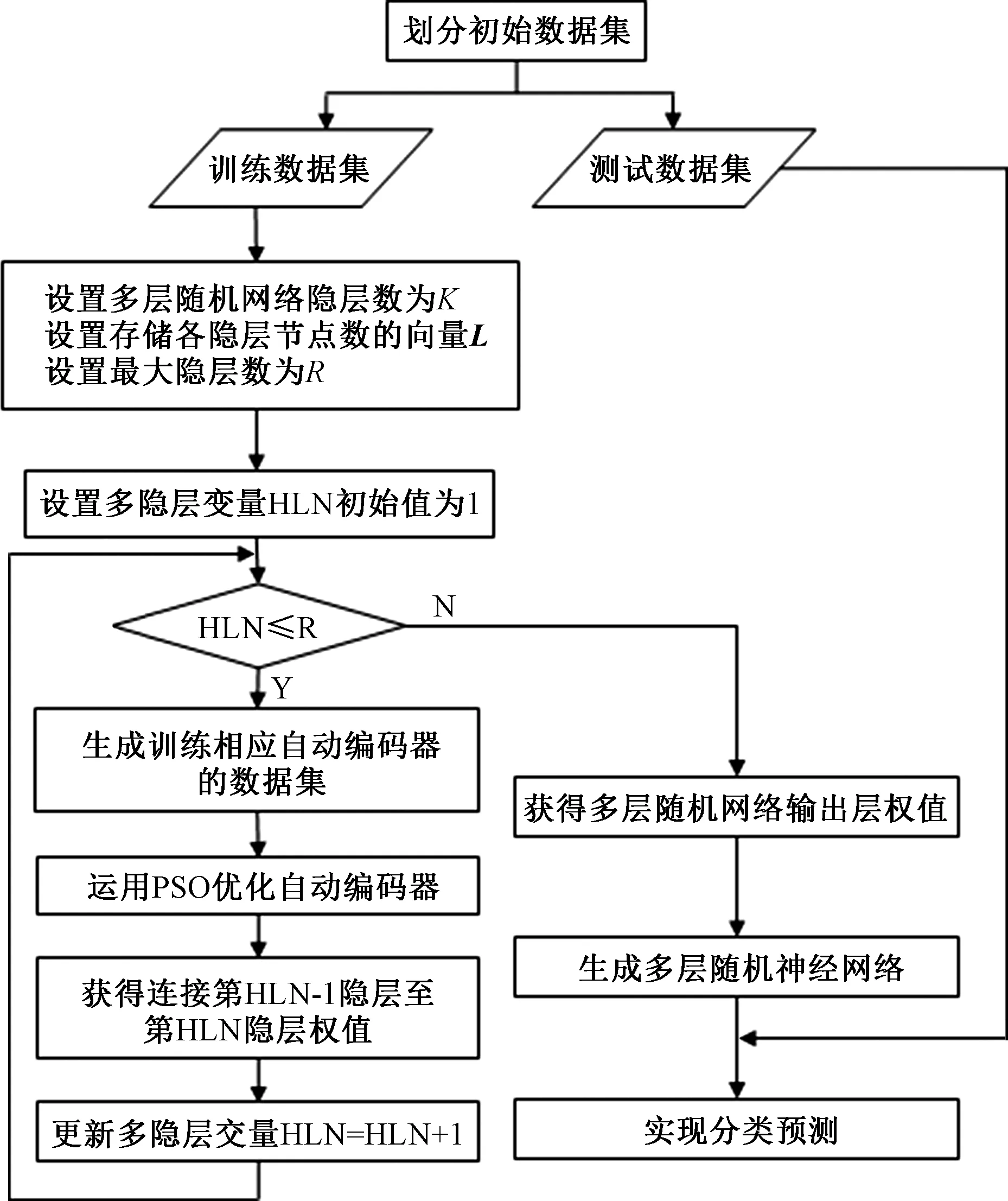
图2 基于PSO的多层随机神经网络框图Fig.2 Frame of multi layer random neural network based on particle swarm optimization

PSO-ML-ELM算法步骤如下:

步骤1:确定多层网络结构．设置多层随机神经网络各层隐单元节点数Li(i=1,2,…,k)．划分原始数据集为训练集和测试集．

步骤2:计算多层随机网络第i隐层在原始训练数据集上的输出，生成新的输入数据集DTR{i}．利用PSO构建第i+1隐层,即获得连接第i层和第i+1层的连接权值．初始输入层视为第0层．具体包括以下步骤:

步骤2.1:初始化粒子群．每个粒子的维数为(Li+1)×Li+1,其中Li×Li+1个分量表示自动编码器中输入层连接权,L(i+1)个分量表示自动编码器中各隐单元的阈值,粒子各分量在[-1, 1]之间随机取值;设置每个粒子的初始飞行速度、粒子的最大飞行速度和种群最大迭代次数;每个粒子的个体最优历史位置为粒子当前位置;随机选取一粒子位置为当前种群全局最优;设置优化目标．

步骤2.2:计算各粒子适应度值,更新各粒子的个体历史最优和种群的全局最优粒子．为了避免过学习,粒子的适应度函数为相应的自动编码器利用超限学习机算法在训练集上的五折交叉验证准确率．为了使自动编码器具有良好的泛化性能,在考虑自动编码器分类性能的同时适当降低网络的输入输出灵敏度,文献[8]中采用式(11、12)更新粒子的个体最优和种群的全局最优粒子．

(11)

(12)

式中：f(Pi),f(Pib) 和f(Pg)分别为第i个粒子、第i个粒子个体最优粒子以及种群全局最优粒子的适应度函数值；senpi,senpib和senpg分别为第i个粒子、第i个粒子个体最优粒子所代表的单隐层前馈网络的输入输出灵敏度值．λ>0为容忍系数．

步骤2.3:根据基本PSO粒子速度位置更新公式更新粒子．

步骤2.4:对步骤2.2到步骤2.3反复迭代,直到达到预定的优化目标或达到最大的迭代次数．以种群全局最优粒子对应的自动编码器的输出层权值作为链接多层随机网络第i隐层和第i+1隐层的连接权,而自动编码器输出层权值 可根据SVD方法由式(13)来计算:

(13)

式中：Hi为多层随机网络第i隐层的输出；H为自动编码器隐层输出．而多层随机网络第i隐层和第i+1隐层的连接权为(βi+1)T．

步骤3:重复步骤2直至构造出第k隐层．

步骤4:在第k隐层上增加输出层,连接第k隐层和输出层的权值βk+1直接通过式(14)来计算:

(14)

式中：Hk为多层随机网络第k隐层的输出；t为期望输出．最终生成多层随机神经网络．

步骤5:利用带惯性权重的PSO对上述多层随机神经网络的各层权值作简单优化,即通过较少的迭代次数对各层权值作微调,生成最终的多层随机神经网络．

不妨假设PSO的最大迭代次数为ITmax,种群大小为Npso,则算法PSO-ML-ELM的时间复杂度为O(K×ITmax×Npso),而隐层数目K通常为一常数,故算法PSO-ML-ELM的时间复杂度为O(ITmax×Npso)．

相对于传统的ML-ELM,PSO-ML-ELM在逐层获取各隐层权值时利用PSO对相应的ELM-AE中输入层权值进行优化,这在一定程度上增加了建立多层随机网络的时间开销,但提高了多层网络的分类性能．相对于传统的深度神经网络,PSO-ML-ELM不需要反向微调网络各层权值,这在一定程度上又降低了时间开销．

3 实验结果与分析

为了验证算法PSO-ML-ELM的有效性,对算法PSO-ML-ELM、深度ELM以及其他流行的深度学习算法进行比较．实验运行的软硬件环境为:Intel-i7处理器,32GB DDR3内存,Windows 10操作系统,Matlab 2013b．

3.1 与ML-ELM的比较

文中在Diabetes、Wine、Satellite image和Image Segmentation 4个相对较小的基准数据集上,验证文中提出算法的有效性．实验中,深度随机网络中隐层数为3,具体各隐层神经元数目设置如表1．在PSO-ML-ELM中,PSO的参数设置为:c1=c2=1.49,种群最大迭代次数为10,种群大小为20．表中，N1、N2和N3分别表示深度随机神经网络第1隐层、第2隐层和第3隐层中隐单元个数．其设置与文献[9]中一致,表1中ML-ELM在4个数据集上的测试精度来源于文献[9]．

算法ML-ELM和PSO-ML-ELM在4个基准数据集均获得优于单隐层随机神经网络的分类精度,这说明深度随机神经网络更能提取有效的数据特征．相对于传统的深度随机神经网络,PSO-ML-ELM在4个数据集上均能获得更优的预测准确率;但训练网络的时间大大提高,这是由于PSO对各个自动编码器优化所导致．

表1 基准数据集上PSO-ML-ELM与ML-ELM算法的性能比较

对PSO-ML-ELM在以上4个基准数据集上各隐层单元数目进行讨论,为了便于可视化,假定第1隐层和第2隐层单元数目相同．从图3中可以看出,PSO-ML-ELM在按表1中所定的隐单元数目设置深度随机网络的结构时均获得较好的预测精度．

3.2 与其他深度学习算法的比较

在MINST数据集上对PSO-ML-ELM与其他流行的深度学习算法进行比较,包括SAE、SDE、DBN、DBM、MLP-BP和ML-ELM．PSO-ML-ELM中PSO参数的设置与3.1节中一致．ML-ELM和PSO-ML-ELM中第1隐层、第2隐层和第3隐层神经元的个数分别为700、700和15 000;输入层到第1隐层、第1隐层到第2隐层、第2隐层到第3隐层、第3隐层到输出层的脊参数C分别设为1e-1、1e-10、1e4、1e7．DBN的网络结构为784-500-500-2000-10,DBM的网络结构为784-500-1000-10．为了便于比较,以上参数的设置与文献[4]中一致．

图4给出了ML-ELM和PSO-ML-ELM第1隐层输出权值的可视化结果,图中描述的是网络第1隐层的输出,每个输出由一个子图代表,共有700个子图．此图表明这两种方法能提取图像的有效特征．

表2给出了不同算法在MNIST数据集上的性能表现,其中DBN和DBM实验结果来源于文献[4],该实验结果是在Intel-i7 2.7GHz处理器,32GB DDR3内存,Matlab 2013a环境下获取的,实验环境基本一致,因此具有可比性．从表2可以看出,基于PSO优化的深度随机神经网络在MINST数据集上的收敛精度优于SAE、SDE和ML-ELM,但略低于DBN和DBM．从时间开销来说,PSO-ML-ELM要远低于DBN和DBM;但相对于ML-ELM、SAE和SDE有较大幅度增加,这是因为引入PSO进行优化增加了时间开销．

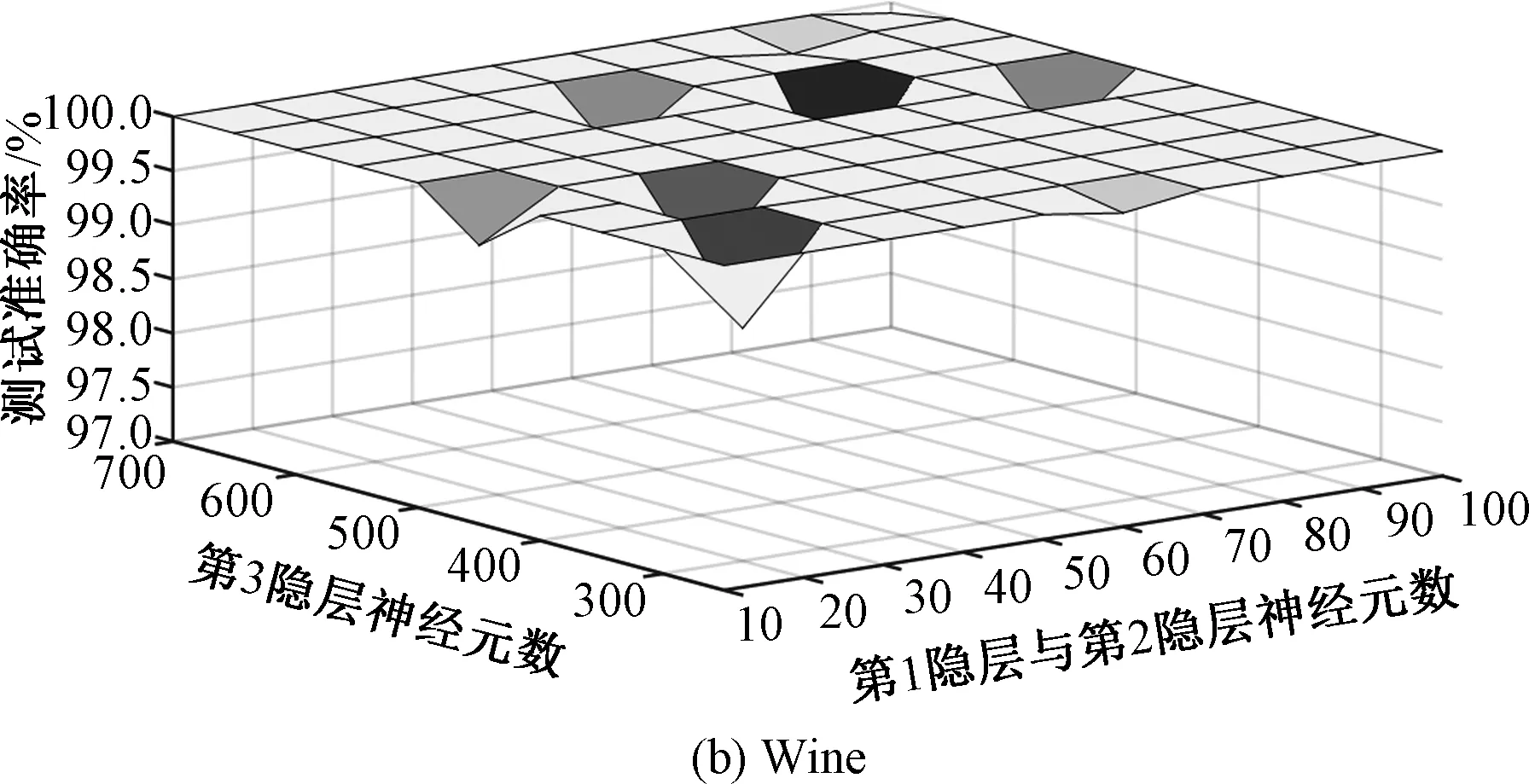
图3 基准数据集上PSO-ML-ELM中各层隐单元数目与测试精度的关系曲线Fig.3 Relationship curve between the hidden neuron number in different layers in PSO-ML-ELM and test accuracy on benchmark data

图4 两种深度随机神经网络第一隐层输出权值可视化Fig.4 Visualization of the first hidden layer output weights on two deep random neural networks

表2 不同算法在MNIST数据集上的性能表现

相对于传统的多层ELM,文中提出的算法提高了预测准确性;相对于DBN与DBM它又提高了训练速度．因此,与其他流行深度学习方案相比,PSO-ML-ELM是一有效的深度学习框架．

4 结论

(1) 文中利用粒子群优化算法结合网络输入输出灵敏度对自动编码器的输入层权值进行优化,从而改善自动编码器的性能以改善多层随机神经网络的性能．最后利用PSO对整个网络的权值作适当优化,进一步提高深度随机神经网络的性能．在不同数据集上的实验结果验证了文中提出方法的有效性．

(2) 尽管文中提出的方法在分类性能上有一定的改善,但也增加了时间开销,下一步工作将考虑如何降低优化代价．另外，文中算法运用标准的PSO进行优化,下一步工作将考虑如何针对深层随机神经网络具体的优化目标设计PSO算法,以更大限度地提高深度随机神经网络的性能．