钢骨超高强混凝土框架结构恢复力模型研究
张建成,曹茂森,贾金青,徐 浩
(1.江苏科技大学 船舶与建筑工程学院, 江苏 张家港 215600;2.河海大学 力学与材料学院, 江苏 南京 211100;3.大连理工大学 海岸与近海工程国家重点实验室, 辽宁 大连 116024)
超高强混凝土随着众多的高层、超高层建筑的兴建,愈发得到深入研究[1-3]。钢骨超高强混凝土结构不仅耐火性好、自重较轻,而且承载力高、变形能力强,其在高层、超高层建筑中越发广泛应用[4]。研究表明,SRUHSC组合框架结构具有优越的抗震性能[5-6],但由于SRUHSC结构内部构造较为复杂,国内外学者对其抗震性能研究仍未成熟[7-12],造成SRUHSC结构的理论研究远滞后于工程实际所需,因此,建立合适的恢复力模型,对深入研究SRUHSC结构的受力机理具有重要的理论意义和应用价值。
本文基于SRUHSC组合框架结构低周反复加载试验的研究成果[4],通过引入循环退化指数,建立能反映循环退化效应的SRUHSC框架结构的恢复力模型,以期为SRUHSC结构的抗震性能研究提供理论参考。
1 荷载-位移骨架曲线模型
文献[4]中SRUHSC框架顶点侧向位移Δ及各层间侧向位移Δi(i=1,2,3)分别与水平荷载P的骨架曲线,如图1所示。据此宜采用三折线简化模型(假设正、反向骨架曲线对称),如图2所示。
(1)
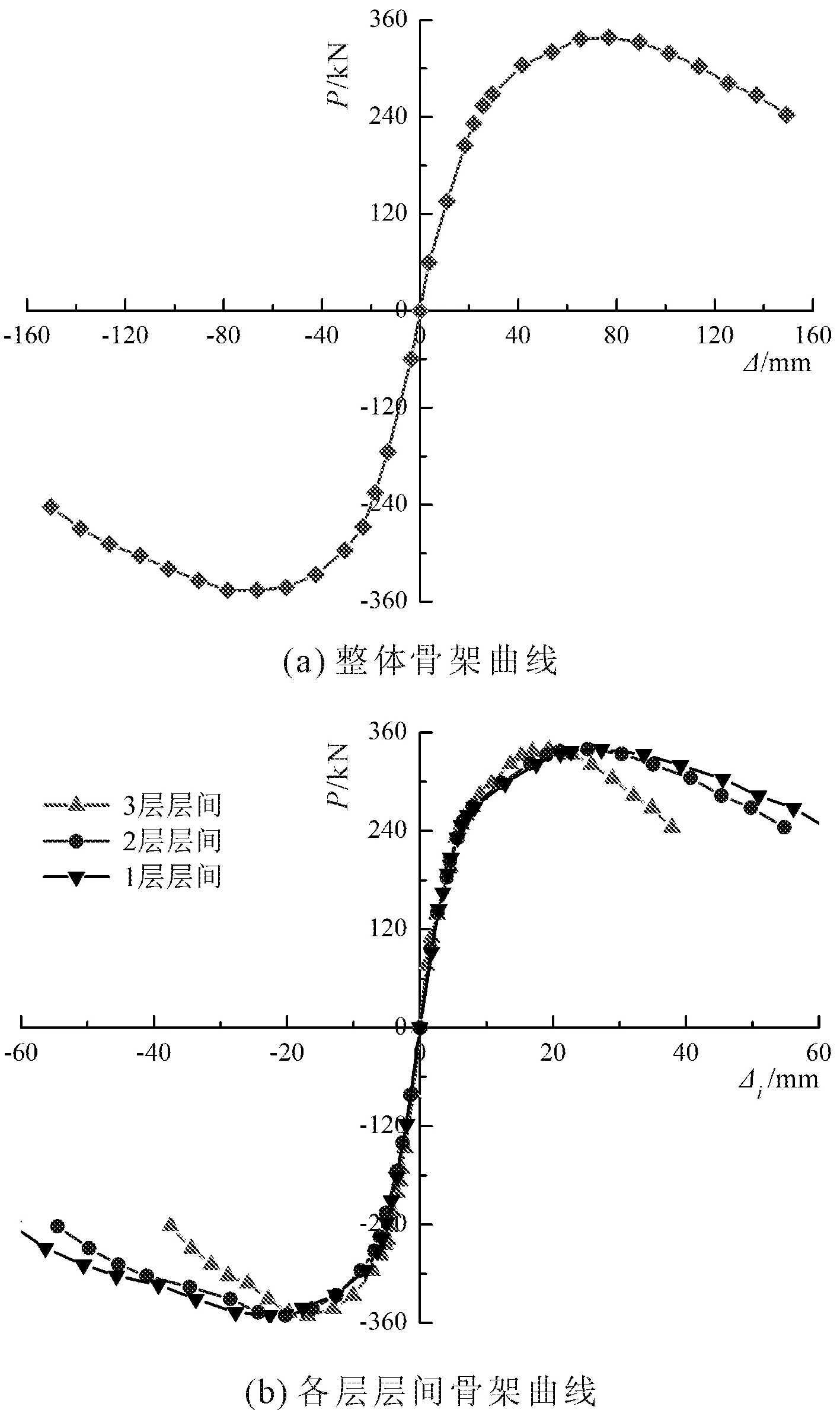
图1 SRUHSC框架骨架曲线
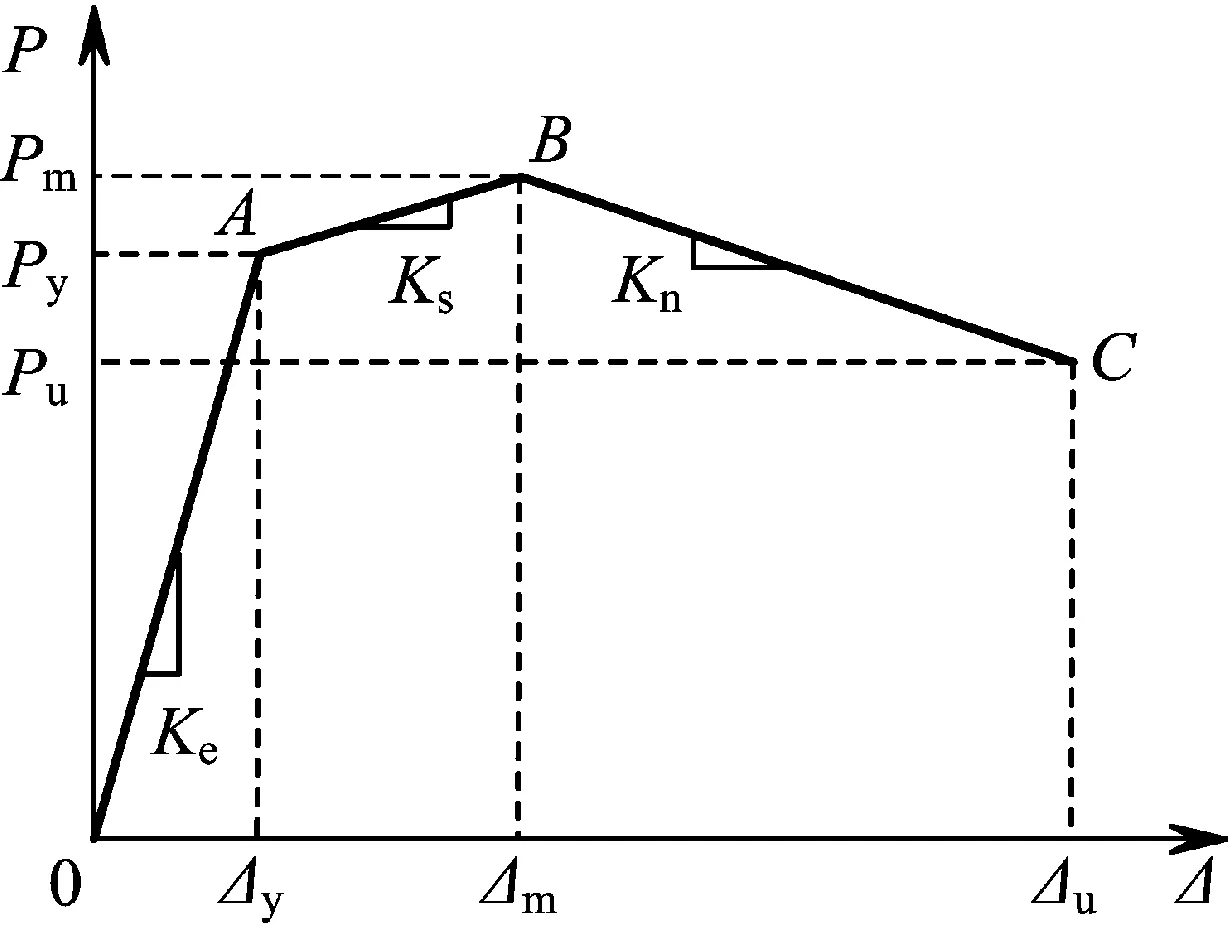
图2 骨架曲线及其特征点
该模型主要分为弹性、强化及下降段。其中,A点为弹性极限;B点为水平荷载峰值。用方程可表示为:
(1) 弹性刚度Ke为骨架曲线中坐标原点(0,0)与屈服点(ΔA,PA)的斜率。
(2) 强化刚度Ks为骨架曲线中屈服点A(ΔA,PB)与峰值点(ΔB,PB)的斜率,表示结构屈服后的刚度效应,Ks与Ke关系为:
Ks=αsKs
(2)
式中:αs由试验测得,表示Ks与Ke的比例系数。研究表明,钢筋混凝土结构、钢结构的强化刚度比例系数αs分别为0.03和0.1[13-14],基于文献[4]的试验结果,本文对SRUHSC框架结构的αs取0.176。
(3) 软化刚度Kn为骨架曲线刚度下降段,通常表示结构水平承载力达到峰值后的衰减梯度。软化刚度Kn与弹性刚度Ke关系为:
Kn=αnKe
(3)
式中:αn为Kn与Ke的比例系数。研究表明,αs对于一般的钢筋混凝土结构、钢结构分别取-0.24、-0.03[13-14]。基于文献[4],本文对SRUHSC框架结构αn取-0.107,该值明显高于钢筋混凝土结构,低于钢结构,表明:进入负刚度段,SRUHSC框架结构的承载力显著优于钢筋混凝土结构,衰减较慢。
2 恢复力模型与滞回规则
2.1 结构恢复力模型
如前所述,对于SRUHSC结构的骨架曲线本文采用三折线恢复力模型,为更好地表征此结构在各加载段抗震能力的退化特性,本文引入循环退化系数βi[15]:
(4)
(5)
(6)
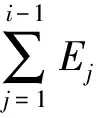
2.2 滞回规则
基于文献[4]的研究,SRUHSC框架结构刚度退化的滞回规则可归纳为以下四步:
(1)强化段规则。硬化段退化规则分为:屈服荷载Py退化和强化刚度Ks的退化。引入βi,结构屈服荷载Py的退化可表示为:
(7)
(8)

结构强化段刚度退化示意,如图3所示,其表达式为:
(9)
(10)
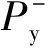

图3 结构强化段退化规则
(2)软化段规则。类似于规则(1),结构软化段退化规则也分为:峰值荷载Pm的退化和软化刚度Kn的退化。同样引入βi,结构屈服荷载Pm的退化规律可表示为:
(11)
(12)

结构软化段刚度退化示意,如图4所示,其表达式为:
(13)
(14)


图4 结构软化段退化规则
(3)卸载刚度退化规则。结构水平承载力未达峰值前,卸载刚度Ku与初始刚度Ke相同,待进入负刚度后,其Ku开始退化。结构卸载刚度退化示意,如图5所示。该退化规则表达式为:
Kui=(1-2βi)Ku(i-1)
(15)
式中:Ku(i-1)与Kui分别为结构第(i-1)、i次加载的卸载刚度。注意式(15)中未标正负号,表明结构在弹塑性阶段,往复加载过程中,具有相同的卸载刚度。
图5中,结构在推向加载完成后达到点3,此时结构处于弹性阶段,其卸载刚度为弹性刚度Ke;反向加载至点6卸载,结构进入弹塑性阶段,计算βi,根据式(15),结构卸载刚度由Ke降至Ku1。

图5 结构卸载刚度退化规则
(4)再加载刚度退化规则。异于以往恢复力模型,本文结构再加载刚度退化规则示意,如图6所示。为更准确地描述再加载时结构刚度的进一步退化,本文运用循环退化系数βi,假定一个目标位移参数,使结构再加载时滞回规则指向该目标参数,其数学表达式为:
(16)
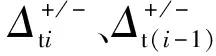
图6中,结构在推向加载完成后达到点3,计算βi,再据式(16),结构反向时,指向目标位移参数点5,正向再加载时,则指向目标位移参数点7。本次加载循环中结构再加载刚度退化的幅度由点6—点2的斜率降至点6—点7。
3 恢复力模型的验证
利用MATLAB编写恢复力模型的程序,将模拟的滞回环与文献[4]的试验结果进行对比,如图7所示。结果表明:两者吻合程度较好,验证了该模型对SRUHSC框架结构的正确性。同时,衡量恢复力模型的优劣还可通过其计算的结构耗能参数是否与试验值吻合,目前常用抗震耗能参数有heq、ζ、Iw。图8给出SRUHSC框架结构各抗震耗能参数试验值与模拟值的对比。结果表明,各参数两者比值均接近于1,吻合度较好,最大偏差是功比指数Iw在破坏荷载点时产生,仅为9.20%,这也进一步验证该模型对SRUHSC框架结构抗震弹塑性分析的有效性。

图6 结构再加载刚度退化规则
4 结 论
(1)本文建立考虑加载循环退化效应的恢复力模型,通过对比P-Δ滞回环以及heq、Iw、ζ三个抗震耗能指标参数的模拟值和试验值,验证了该恢复力模型的正确性和有效性,可为SRUHSC框架结构弹塑性分析提供一定的理论依据。
(2)本文建议的模型,能较好地反映SRUHSC框架结构在低周反复荷载作用下的主要受力过程及其受力特征,可较为准确地描述SRUHSC框架结构强化、软化、卸载及再加载各阶段刚度的退化,以及该框架结构屈服荷载、峰值荷载的退化,可为SRUHSC框架结构抗震性能的研究提供一定的理论参考。

图7 滞回曲线计算值与试验值的对比

图8 SRUHSC框架各耗能参数试验值与计算值对比

