PCA与ELM模型相结合的矿井突水水源快速识别方法研究

孙文洁，杨 恒，李 祥，王子超，杨 蕾

(1．中国矿业大学(北京) 地球科学与测绘工程学院，北京 100083；2.核资源与环境国家重点实验室(东华理工大学)，江西 南昌 330013；3.中国环境科学研究院 环境基准与风险评估国家重点实验室，北京 100012)

矿井突水事故频发一直威胁着人类的生命财产安全。目前，众多学者已研究出多种突水水源识别方法，如主成分分析与贝叶斯判别法相结合突水水源判别模型[1]；基于主成分分析和Fisher判别分析理论的突水水源识别方法[2]；模糊综合评价[3]等。这些方法已广泛应用于矿井水害的防治，但矿区水文地质条件复杂，这些方法也均有各自的适用性。如Fisher适用于对样本总体不做出要求的矿区；模糊综合评价适合做多因素的样本分析；贝叶斯判别法适用于样本主成分明显的情况。

BP神经网络利用误差反向传播的方法确定权值，可以模拟人脑信息处理的方法，从大量庞杂的数据中找出规律，适用于处理非线性问题[4-6]，在突水水源识别中已大量运用[7-10]。但由于算法的收敛速度慢，且初始权值和阈值的设置对结果影响较大等问题，使其容易降低结果精确度甚至误判。极限学习机(Extreme Learning Machine，ELM)是一种简单高效的单隐层前馈神经网络学习算法[11]。ELM在训练过程随机选取一次网络初始连接权值和阈值，通过模型迭代获得唯一输出权值。ELM算法学习速度快，有效的克服了传统BP算法的不足，已在多个领域广泛应用[12-14]。

主成分分析(PCA)利用降维的思想，从多个指标中提取主要特征指标，消除水样中各水化学指标间复杂信息的影响，从而以少量综合指标反映了大量原始变量信息。本文利用PCA对赵各庄矿水样中各水化学指标数据进行降维处理，找出各水源水样的主控因子，以便更准确的确定赵各庄矿不同含水层的水样特征。在此基础上，利用ELM对水样中的主控因子进行仿真模拟，以期增加ELM算法的训练速度及精度，为赵各庄矿及开滦矿区相似矿井提供技术支撑。

1 研究方法

由于矿区水样成分复杂，通过主成分分析可在保留原始主要信息的基础上找出水样中的主要影响因子，减少水样中多余指标的影响，再通过极限学习机对水样进行分类，识别方法快速，且增加了识别的精确度。

1.1 主成分分析法

设原始数据矩阵X的p个向量X1、X2、…、Xp的线性组合为Y=AX，即：

其中，ai1+ai2+ai3+…+aip=1；Yi与Yj(i≠j；i、j=1，2，…，p)之间不相关；Yi是(Y1、Y2、…、Yp)的一切线性组合方差最大，Y2是与Y1不相关的X1、X2、…、Xp的一切线性组合中方差最大的组合；Y1、Y2、…、Yp的方差之和等于X1、X2、…、Xp的方差之和。

1)首先将原有变量数据标准化，然后计算各变量之间的协方差矩阵∑。

2)计算好的协方差矩阵特征向量为λ1≥λ2≥，…，≥λp，相应的单位特征向量为T1、T2、…、Tp。转换矩阵为A=T′，j即A的第i行就是∑的第i大特征根对应的单位特征向量Ti。且第i个主成分Yi的方差就等于∑的第i大特征根λi。

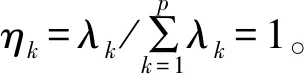
4)在选取主成分个数时，一般取决于累积方差贡献率。通常取主成分使得方差的累积贡献率达到80%以上[15]。

1.2 极限学习机

ELM是一种新型的快速学习算法，学习过程中只需随机选取一次输入权值和隐含层神经元偏值，确定隐层神经元的个数，即可计算求出最优输出权值，进而得到最优学习输出值[16]。其基本原理及算法学习步骤如下[17]：

设有n个任意的训练样本(xi，ti)，其中i=1，2，…，n；xi=[xi1+xi2+xi3+…+xin]T∈Rn为输入向量；ti=[ti1+ti2+ti3+…+tim]T∈Rm为期望输出向量；隐含层神经元个数为L；隐含层神经元输入权重为Wi；隐含层神经元的阈值bi。

则隐含层输出矩阵为：

式中，g(x)为激活函数；Wi·xj表示Wi和xj的内积。

在ELM算法中，一旦输入权重Wi和隐含层的偏置bi被随机确定，隐层的输出矩阵H就被唯一确定。训练单隐层神经网络可以转化为求解一个线性系统Hβ=Z。并且输出权重β可以被确定：

式中，H+为矩阵H的Moore-Penrose广义逆；Z为期望输出。

2 数据选取

赵各庄矿作为开滦矿区地质条件最复杂的矿区，矿井涌水问题一直为其开采工程中最大的影响因素之一，特别是矿区内即将开采的14水平底板距离奥灰顶板太近，因此开采过程中发生突水概率大大增加。基于以上问题，选取赵各庄矿作为示范区，对本文所述识别方法展开研究。

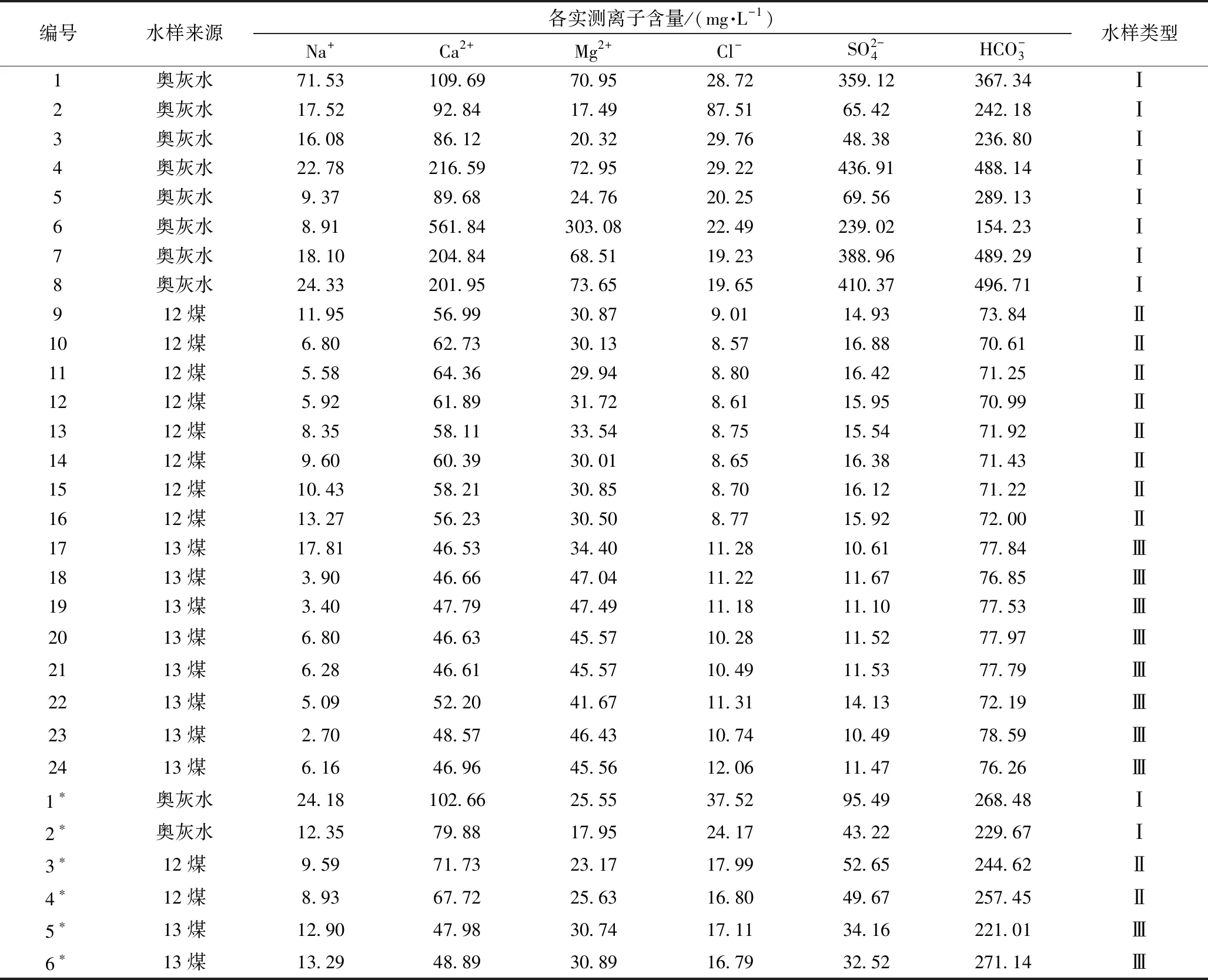
表1 赵各庄矿水样实测数据表

3 结果分析

为排除水样中冗杂信息及水样影响度较小指标的影响，对表1训练样本数据进行了主成分分析，得出其相关系数矩阵见表2，各个成分解释方差率见表3。由表3可知，前三个成分的方差贡献率较大，且累积方差贡献率达91.868%，故认为在赵各庄矿的各离子中，前三种阳离子对水样的影响较大，因此在后续的研究中只考虑了阳离子的影响，即选取前三种阳离子作为水样的主成分来对样本进行仿真训练。

表2 各水化学指标的相关系数矩阵

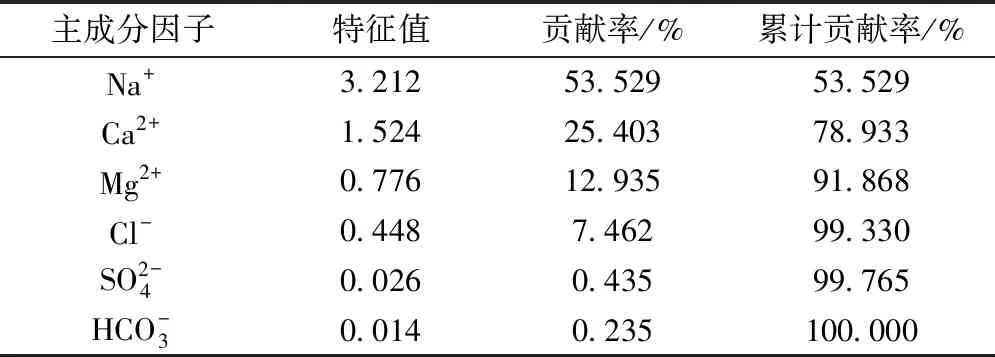
表3 各成分解释方差率

3.1 MATLAB仿真训练

输入为三种主成分离子的含量值，即设置网络的输入层节点数为3；输出为3种水样类型，即设置网络的输出层节点数为3；为使ELM训练结果以最小的误差逼近所有训练样本，故设置隐含层神经元个数等于训练样本个数即为24；网络的输出状态为3，对应三个待识别的层位。

本文ELM模型中S型函数(Sigmoid)为隐含层神经元的传递函数，均方误差(mse)为性能函数，利用ELM算法对样本进行训练，设置ELM的应用类型为1，即分类识别。将主成分分析所得的水样三种主成分数据导入ELM模型中，使用MATLAB软件对测试样本进行仿真训练，模型在10s内即得出水样分类结果，最终水样识别结果见表4。

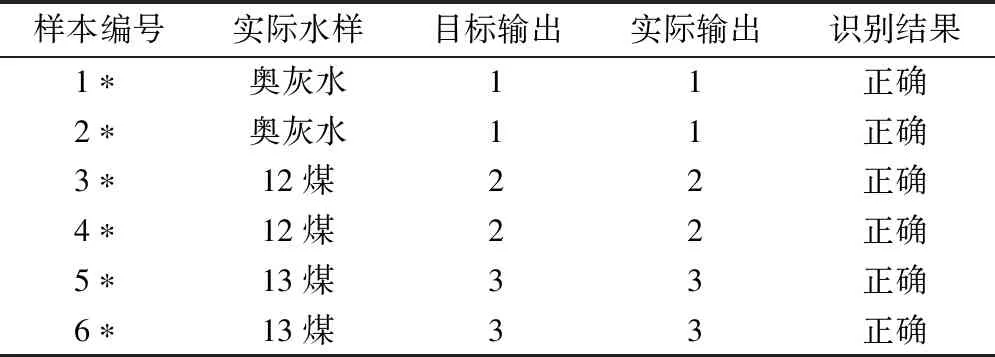
表4 ELM识别结果

水样分类结果表明，测试样本的识别正确率高达100%，说明PCA-ELM相结合的矿井突水水源方法分类识别性能好，在赵各庄矿具有一定的应用价值。

3.2 结果对比

为了对比算法的优劣，同时对表1的样本数据使用了BP神经网络进行仿真训练，设置输入层神经元个数为3，对应Na+、Ca2+、Mg2+三种主成分，根据Kolmogorov定理[18]可确定隐含层神经元个数为7，将网络的两种输出状态编码为：奥灰水(1 0 0)、12煤(0 1 0)、13煤(0 0 1)，所以设置输出层神经元个数为3，因而BP网络的结构即为“3-7-3”型，采用tansig作为隐含层传递函数，采用logsig作为输出层传递函数，采用trainlm作为训练算法，采用均方误差(mse)作为性能函数，训练目标取0.01。

由于无法准确获取BP网络中的初始连接权值和阈值，故初始权值和阈值为随机选取，通过MATLAB软件对测试水样进行仿真测试，得到测试样本的识别结果见表5。对比表4、表5可知ELM网络的训练结果准确率高，即表明ELM的识别精度比BP网络有所提高。

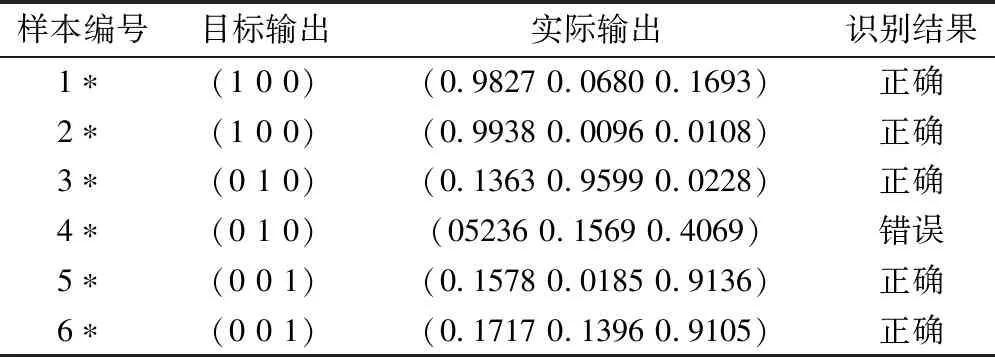
表5 BP网络识别结果

由于极限学习机在训练过程为随机选取网络初始连接权值和阈值，产生的参数可能会对输出的权值造成误差或者造成模型网络不稳定，从而降低结果精确度，因此，在后续研究中还需对此进行改进，以期克服该问题。

4 结 论

1)通过对赵各庄矿水样进行主成分分析，选取了Na+、Ca2+、Mg2+作为具有代表性的水样主成分数据，排除了原始水样数据大量冗余信息的影响。

2)采用主成分分析确定的赵各庄矿水样3种离子的数据进行ELM模型仿真训练。ELM模型可在10s内得出仿真训练结果，且结果准确率高达100%，说明该方法可行性高，可用于矿井突水水源识别。

3)将PCA-ELM模型与传统BP神经网络进行对比，传统BP神经网络仿真训练结果准确率为83.33%，远低于PCA-ELM模型仿真训练准确率。因此，本文提出的PCA-ELM相结合的矿井突水水源识别方法不仅学习速度快且训练结果准确率高，为矿井突水水源识别提供了新的方法与思路。

4)本文所述方法不仅克服了制约传统BP网络学习过程中受初始权值和阈值影响的问题，而且对极限学习机进行优化，排除了水样各种冗余信息对模型精度的影响。通过对示范区进行仿真训练，结果准确度高达100%，为开滦矿区相似矿井的水害防治工作提供了技术支撑。但由于ELM算法随机给出初始参数的问题，在以后的使用中可能会出现模型网络不稳定的情况，故需继续改进，以期克服此方面的不足。