地震波传播特性研究综述
1 引言
近年来,中国地震自然灾害频繁发生,其中以西部地区的地震活动最为强烈,频度最高,造成大量的人员伤亡和经济损失。关于地震波传播的研究是地震工程领域的热点问题。地震波传播理论强调的是波的传播与媒介之间的关系,经过国内外众多学者对该领域的长期研究,地震波传播理论和研究技术得到了长足发展,也取得了很多有价值的研究成果,并在地震领域得到了广泛的应用,但仍有很多理论体系不够完善,结论不够成熟,需要进一步研究。
2 地震波传播理论
地震波理论是各地震学科的基础和重要内容,它强调波的传播与媒介之间的关系,涵盖了人工地震探测与信息技术等众多领域。起初关于地震波传播理论的研究,是建立在地球是一个均匀且各向同性的完全弹性体的条件假设基础上进行的,这势必会导致最终的理论成果的特殊性。由于实际的地球地层介质是由复杂介质组成的非完全弹性体,不能将其简单地归结为各向同性的均匀完全弹性体,这也导致了地震波传播特性研究的复杂性。基于这一点,人们在完全弹性介质中地震波传播理论的基础上,考虑到地层介质的复杂性,推导出了地震波在复杂地层中传播的数学理论模型,并结合数值分析方法,对地震波传播进行研究,实现对地震波传播理论和研究方法的拓展与创新。目前,地震波传播理论被广泛应用于震源参数测定、地震近场问题、地球内部构造研究等方面。
2.1 弹性介质中地震波传播
弹性介质是最基本也是最经典的一种介质模型,目前地震学或弹性波众多应用领域均是以这种模型为基础。陈运泰[1]将Haskell 展开式与Hansen 矩阵法结合起来,得出多层均匀介质各向同性完全弹性半空间中一般类型的震源引起的位移场的形式解。丛相文[2]等应用Fourier 变换法研究了非均匀弹性介质波动方程正演的解,并模拟地震波的传播。方刚、张斌[3]从弹性体的Navier 方程出发,推导出弹性介质的Lagrange 方程,并对该方程进一步推导得到地震波在均匀和非均匀介质中传播的波动方程,该方程常用作地震波传播规律研究和解决相关地震勘探问题的基础。2017 年,方刚[4]等在Hamilton 理论基础上建立了Hamilton 正则方程和地震波动方程,被作为基础理论应用于地震领域的相关学术研究。
2.2 黏弹性介质地震波传播
地震波在黏弹性介质中传播特性与实际地层中传播特性很相似。由于实际地层介质的黏弹性质,使得地震波在传播过程中,随着时间和传播距离的增加出现衰减现象。
1845 年,Stokes 首先建立了黏弹性波动方程,后来发展形成了Maxwell 黏弹性模型和Kelvin 黏弹性模型。但这2 个模型都存在缺点,Maxwell 模型更接近于黏性流体介质,Kelvin模型接近于弹性固体介质,这2 种模型的本构关系都不能完全符合实际底层的情况。因此,国内外的研究人员对该理论模型进行不断的改进,并提出更加近似于实际地层情况的介质模型。蔡袁强[5]、徐献芝[6]、严红勇[7]、贾立坤[8]等充分考虑了包括地下水、孔隙比等因素的影响,在模型本构方程中加入介质的黏滞因素,推导出符合实际的Kelvin-Voigt 黏弹性体模型对应的波动方程,并结合数值模拟方法进行求解,研究地震波在地层中的传播特性。邓巧琳[9]基于Kelvin 黏弹性介质模型(见图1),推导出介质的反、透射系数和能量滞留比公式,研究地震波能量衰减具有一定的参考价值。
P 波入射能量滞留比:

SV 波入射能量滞留比:

SH 波入射能量滞留比:

式中,s 为能量衰减比;R 为发射系数;T 为透射系数;α 为介质波阻抗比。
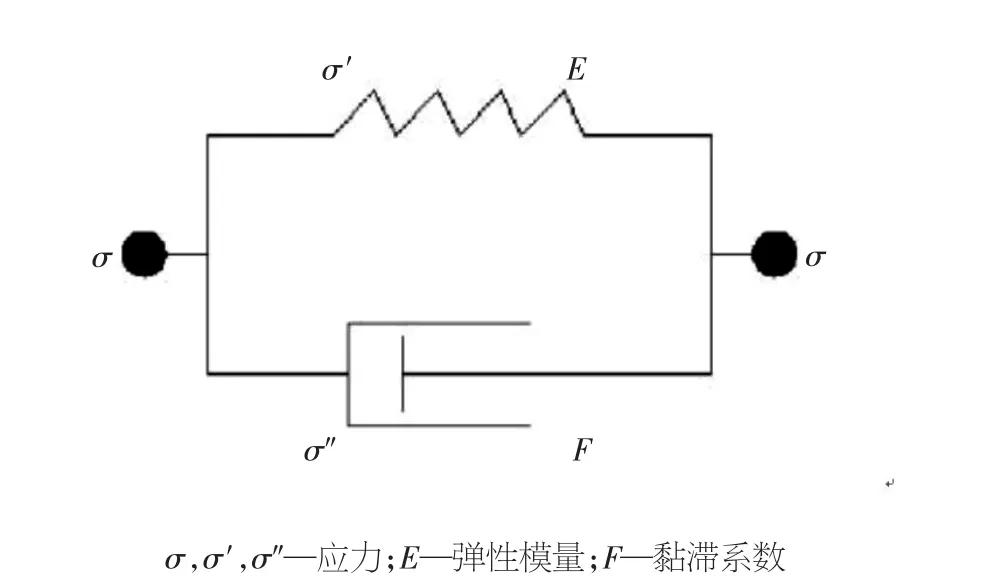
图1 Kel vi n 黏弹性介质模型
虽然对Kelvin 介质模型在不断的改进,但还是与实际的地层情况存在着一定差别,使得研究人员重新构建新的介质模型。Aki 和Richards[10]提出的标准线性黏弹性固体模型(见图2),综合了Maxwell 黏弹性模型和Kelvin-Voigt 黏弹性模型两者的特点,将原有模型的缺陷加以改善,使新的黏弹性模型能更符合实际情况。

图2 标准线性黏弹性介质模型
标准线性黏弹性模型本构方程与初始条件:

式中,τs为应力松弛时间;τσ为应变蠕变时间;u(t)为应变;ER为弹性松弛系数。
范家参[11]对标准线弹性固体模型介质中地震波动方程求出了解析解。刘铁林[12]提出该介质模型波动方程的数值模拟显式算法,该算法具有计算快,精度高等特点。高强[13]将精细积分法和虚拟激励法相结合,形成新的数值计算方法,用于求解三维各向同性黏弹性介质中传播问题。
除此之外,郭智奇[14]等建立了以Boltzmann 叠加原理为基础的积分型本构方程及波动方程,并求出二维黏弹性平面波解。通过该模型求解可以得到反射和透射系数,研究介质分界面的反、透射问题。邵志刚[15]等以三元黏弹性介质模型(又称Poyting-Thomson 模型)理论和本构方程为研究基础,对地震波传播进行理论分析,并采用叫错网个有限差分法进行数值模拟。结果表明,地震波在黏弹性介质中传播,纵波的衰减速度大于横波。学者高宇航通过引入记忆变量的方式推导出弹性VTI 介质和黏弹性VTI 介质的波动方程;以交错网格有限差分的数值模拟方法,确定差分稳定性条件。该方法计算量小,所需内存少。
2.3 弹塑性介质地震波传播
由于地震动荷载作用,部分地层介质进入弹塑性阶段,对于这部分地层中地震波问题研究,主要是对弹塑性动力反应问题进行求解。
1952 年,Wood 以弹塑性杆件中一维应力纵波理论为基础,进行推广,得到一维应变弹塑性波的波动方程。学者王礼立弹塑性波动问题提出了逐步近似求解方法,该方法具有计算步骤简单,而且不受波速影响的特点。学者孟昭波在弹塑性理论公式的基础上,进行改进,推导出地震波在弹塑性介质中传播新的数学模型和相关求解方法,再通过模型正演的方式研究弹塑性介质中的地震波波场。学者李建功等通过有限元分析软件ANSYS/LS DYNA 模拟了地震波在具有初始应力情况下的弹塑性岩石介质中的传播过程,并分析了该条件下的地震波传播衰减规律。学者李亮等根据在循环荷载下的动力响应特征,对弹塑性本构模型进行了改进,以适应地层介质的实际变化情况。然后通过有限元分析软件ANSYS/LS DYNA 对地震波传播过程进行模拟,并分析了该条件下的地震波传播衰减规律。研究结果表明,地震波的衰减与传播距离呈负指数变化,并指出波形的几何扩散和塑性变形是造成地震波衰减的主要原因。学者李亮等推导了基于SMP 破坏准则对弹塑性=动力本构模型进行改进,并提出了求解弹塑性波动问题的时域显式有限元方法。
3 结语
地震波传播理论经过国内外研究人员的不断研究与创新,其理论体系逐渐完善,理论成果也更加成熟。弹性波动理论多被用作复杂地层中地震波传播的基础,黏弹性和弹塑性介质地震波的传播更能体现实际地层中地震波的传播特性。复杂介质中地震波传播过程十分复杂,常常采用解析解和数值解相结合的方式进行研究。但研究过程中,研究人员在数学理论模型的建立和求解时,往往进行了不同程度的简化,造成了理论和实际之间存在着一定的差异。所以对于地震波传播特性的进一步研究需要考虑更多因素的影响。

