基于GBDT和新型P-GBDT算法的催化裂化装置汽油收率寻优模型的构建与应用

王 伟， 汪 坤， 杨 帆， 戴超男， 金继民， 金宝宝

(1.中国石化武汉分公司，湖北 武汉 430082；2.联想大数据智能应用实验室，四川 成都 610041)

催化裂化(FCC)是炼油厂重质油轻质化的主要工艺之一，该工艺在高温和催化剂的作用下将蜡油和重油转化成液化气、汽油、柴油等轻质油品，在炼油工业生产中占有重要的地位[1-5]。由于催化裂化系统装置工艺复杂，连续程度高，反应机理复杂，其反应过程和产物收率受原料油性质、反应再生催化剂性质以及操作条件相互影响，是一个高度非线性和相互强关联的系统，难以全面地用传统的数学模型来描述[6-8]。近年来，使用基于数据挖掘技术的分析方法成为解决该类问题的新方向[9-14]。

目前，数据挖掘技术被应用于各种行业，包括国内外金融业[15]、互联网[16]、通信[17]、电子商务[18]等，并呈现快速发展的趋势。得益于日益完善的采集装置及数据存储设备，可以采集到各种原料、催化剂、操作条件等实时数据。这些数据可以有效反映催化裂化的反应过程。因此，相比传统的机理分析方法，可以基于数据分析寻找新的优化方式。通过已有数据建立合理的统计学分析模型，对重要指标以及反应过程进行分析，进一步提高原料利用率与对应产品的收率。

近年来，数据挖掘已逐步被用于催化裂化等工艺的优化。李鹏等[19]使用非线性主成分分析法确定了结焦关键性参数，并结合神经网络等预测方法针对结焦趋势构建了结焦诊断模型。Zahedi等[20]基于误差反向传播神经网络和径向基神经网络建立了催化重整的预测模型，并使用单变量优化方法对温度和压力等工艺参数进行优化。Hao等[21]通过多种软测量建模方法分别对相关指标与产品收率进行分析，并使用最小二乘支持向量机(LSSVM)算法建立催化裂化产品收率的预测模型。目前，现有的优化预测模型多由神经网络、支持向量机(SVM)、决策树等算法构建，且用于模型建立的参数多为基于反应原理与生产经验筛选出的经验影响参数。通过对现有方法的研究和改进方法的尝试，发现在模型中仅使用工业经验已知的关键影响参数进行拟合，得到的拟合结果有一定欠缺。其中可直接调控的参数权重较小，不利于模型的改进和实际生产中的寻优。如果在此基础上加入不可控的参数进行训练，则会出现一定的过拟合现象，结论在测试数据以及实际生产中的表现都有所下降。为了改进方法的不足，增大模型中经验可控参数的权重，使模型的拟合泛化能力增强，需要选择建立其他的模型，对催化裂化装置的产品产率进行拟合。

笔者根据某炼油化工公司催化裂化装置提供的实时过程数据，使用GBDT算法建立了基于经验可控指标与重要相关参数的汽油收率预测模型。在该算法的基础上，引入特征权重和采样比率，通过人工调整不同特征在模型中的权重大小以及模型每次迭代时所采用的特征数量，从而调整经验可控指标以及其他指标对模型的影响，优化模型，提高模型的拟合能力和泛化能力。

1 数据预处理

1.1 数据整理格式

笔者以从某石油化工企业的集散控制系统(Distributed control system, DCS)及实验室信息管理系统(Laboratory information management system, LIMS)采集到的数据作为研究对象，进行整理后得到初始数据库。通过LIMS系统采集到从2016年8月4日至2018年3月20日的数据样本，分析频次为每周1次。LIMS数据包括原料油和再生催化剂的性质相关数据。DCS系统装置的采集时间段为2017年10月21日至2018年4月25日共6个月，记录频次约为每15 s 1次，该装置主要采集操作变量和系统物料平衡数据。将采集到的数据按照键值对的格式整理，每条数据由时间戳和指标值2个字段构成，分别保存为键和值，并将所有数据按时间戳进行升序排序，方便进一步清洗及计算。

1.2 数据清洗与插值

采集到的数据需要通过数据清洗来保证训练数据的正确性和有效性，以提高模型运算的效率。由于一些客观原因，如装置测量波动、数据采集系统偶发问题或者人为因素等，原始数据可能存在异常情况，如部分数据存在异常值、缺失、重复、不完整、噪音等，此外，还可能存在部分冗余数据。对于这些异常数据，需要根据经验与对催化裂化工艺参数的理解进行清洗。数据清洗的原则遵循以下几点：

(1)剔除数据格式错误的数据。

(2)利用莱特准则判定异常数据，并使用时间临近数据的加权平均值替代异常值；对于缺省值，也看作异常值进行处理。

(3)统一相同时间戳的记录，选择其中合法的数值并取均值。

通过分析清洗后数据的特点，发现2个采集系统的数据采集频率差异较大，需要对分析指标的监控采集频率进行统一处理。笔者以60 min作为统一间隔，将采集间隔小于60 min的数据进行平均处理，在时间间隔内采样并取该间隔内的均值；将采集间隔大于60 min的指标进行插值处理，合理扩充已有的参数。根据原始数据的特点，一般由DCS装置采集的数据需要进行采样处理，而由LIMS装置采集到数据需要进行插值处理。

为了使插值得到的数据曲线更平滑，笔者采用3种插值方法结合进行插值：(1)直接使用前一次的测量值插值；(2)线性插值；(3)二阶B样条插值。

将采用3种插值方法分别插值后的均值作为最终插值的结果。对于测量值前后差异较大的数据而言，3种插值方法都能有效弥补采样时间段内的缺省值，且处理得到结果值差异不大。将它们的均值作为插值结果，得到的数据稳定性更高，更可能反映出未测量到的趋势。

1.3 特征筛选

经过数据清洗与插值的LIMS和DCS数据包含近2000个分析特征指标，其中包括可控指标和监控所得参数。直接将所有指标应用于产品收率预测，会增大计算的复杂度，影响模型的可解释性、容易出现过拟合，同时可能会降低重要参数的所得权重。因此，筛选收集到的数据特征指标中可能影响产品收率的关键特征指标是一个优化模型特征的过程。此外，进行特征筛选可以有效消除冗余特征，降低训练数据的维度和计算的复杂度，同时提高模型的泛化能力。

筛选模型特征一般从系统工艺流程、催化裂化反应过程以及采集数据自身特点等方面来考虑。笔者将采集数据按照60 min的粒度进行时间对齐，并构建相应的特征筛选算法如下所示。

算法：特征筛选算法。

输入：来自LIMS和DCS的全部分析指标构成的特征总集合A。

输出：筛选后的有效特征集F。

(1)从特征总集合A中删除部分意义重复或无效的特征。

(2)根据行业经验：分析系统工艺流程、催化裂化反应过程筛选特征，选择经过机理验证的对催化裂化过程有重要影响的因素作为特征指标，称为经验可控指标并构成对应集合S1。

(3)依据采集指标与收率的相关性构建filter进行过滤：计算各指标与收率的Pearson相关系数或传递熵，并以此筛选得到部分模型特征。笔者使用Pearson相关性系数计算指标与汽油收率的相关性，选择相关性最高的M个指标，作为特征集合S2。

(4)合并S1与S2所得模型特征，进行特征处理并作为候选特征集F。

(5)选择可对输入特征进行权重打分的机器学习模型构建wrapper用于筛选特征：

选择随机森林算法构建预测模型，使用已有特征集F进行训练，筛选出训练后特征权重最小的m个特征，构成待剔除特征集Q，并移除Q中的经验可控特征，使用Q′更新Q，其中Q=Q′-S1。

对于Q中的每个特征q：

①构建新的候选特征集F′=F-q，使用 K-Folder 交叉验证的方式训练随机森林模型，并与使用特征集F交叉验证得到的训练结果进行对比。

②选择训练结果更好的特征集作为新的F。

③若未遍历完Q中的全部特征，则重复①②；否则，执行(6)。

(6)最终得到的特征集合F为特征筛选结果。

使用该算法筛选特征，结合工业经验，从操作条件、原料、催化剂等方面可以筛选出对汽油收率有重要影响且直接可控的10个经验指标，其中包括原料入口温度控制、提升管出口温度、汽提蒸汽(中)流量和回炼油入提升管流量等。计算指标与汽油收率的Pearson相关性进行筛选，当所得相关系数值高，表明其一定程度上能真实反映或逼近产品收率的变化，可能是影响催化裂化系统中汽油收率的关键指标。部分经验可控指标可能与汽油收率的相关性并不显著，需要结合所得的2个特征集合共同构成候选特征集。

随机森林模型是将多棵决策树集成学习的一种算法，使用该算法构建特征选择模型稳定性较好，在训练中会对特征和样本进行有放回的随机抽样，多次抽样有利于选择到最优的特征。使用交叉验证筛选用于训练的模型特征，剔除了64个特征，其中包括粗汽油入塔-吸收解吸塔、稳定汽油入塔-吸收解吸塔和吸收解吸塔上中段回流流量控制等指标。通过构建模型wrapper对特征进行筛选，得到除经验可控指标外172个模型重要性较高的特征。

通过特征筛选，最终得到182个原始特征指标，可以被应用于特征处理与模型训练。除此之外，为了避免随机波动的影响，增加特征数据的稳定性，笔者通过处理原始特征指标，增加对应的滚动均值作为新的特征。使用简单移动平均的方式计算各特征参数每4 h的滚动均值，忽略累计量的影响，并将滚动均值作为新的特征与原有特征数据合并。得到的滚动均值曲线可以有效平滑可能的异常值以及随机突变，同时反映实际数据的变化趋势。通过对筛选后的数据进行特征平滑，扩增后的总特征数为364，包括原有特征指标与对应的滚动特征均值。

2 现有模型的评估

为评估现有模型，笔者首先采用均值预测，即采用训练集中所有汽油收率的均值作为未来汽油收率的预测值，并以该模型的预测效果作为现有模型评估的基准；其次，采用GBDT算法构建汽油收率预测模型，进行汽油收率预测。

2.1 模型评估指标与寻优方法

仅使用单一评估标准来评价汽油收率预测模型的效果会得到不完全的结论，如仅使用平均绝对误差(Mean absolute error, MAE)，可能多个模型之间的值差异不大，不能够得到明显的判别；同时，也无法反映真实收率与预测值的拟合情况。为了更好地评估回归模型的效果，笔者采用3种方式共同评价模型的准确度和拟合效果：准确率(Precision)、决定系数(R2)和均方根误差(Root mean square error, RMSE)。

(1)

准确率用来衡量预测值与实际值的整体偏差程度，一定程度上而言，准确率越高，模型的预测值与真实数据的偏差越小。

除此之外，由于真实汽油收率的分布近似正态分布，且较为集中，使用历史汽油收率的均值作为预测值的准确率也可以达到97.32%。在使用准确率作为评价标准的基础上，还需要去掉收率的均值来评价收率的变化程度，同时评估模型对汽油收率的预测效果。针对真实汽油收率的整体特点，使用决定系数R2作为评估标准，可以很好地反映预测模型的拟合效果。R2的表达公式如式(2)所示。

(2)

相比R2和准确率，均方根误差表示预测值与实际值误差的平方和与预测次数N比值的平方根，能更好地用来衡量预测值与实际值之间的偏差。均方根误差的值由式(3)计算。

(3)

均方根误差和准确率主要反映预测值与实际值之间的偏离程度;而R2更倾向反映预测值与实际值之间的线性相关性和拟合程度，并与直接使用均值进行预测的效果进行对比。同时使用上述3个评估标准作为指标，可以全面地反映原有模型的预测效果以及寻优模型的改进效果。

2.2 GBDT模型构建

通过Boosting方式集成的梯度提升决策树(Gradient boosting decision tree，GBDT) 算法是一种迭代的决策树算法。其采用加法模型(即基函数的线性组合)，以及不断减小训练过程产生的残差来完成数据分类或者回归。在GBDT算法的基础上，可以对模型进行改进：参考随机森林的思想，对训练特征进行有放回采样，赋予不同的采样权重以保证经验可调的特征对应采样概率更高。为了对比改进方法的模型效果，使用GBDT算法构建模型并训练，将基础模型调优得到的结果作为寻优与改进的基础标准。

笔者采用GBDT算法的开源系统实现lightGBM回归模型，以预测汽油收率为目标建立回归树模型，并将预测结果作为基准值与优化后的模型预测效果进行对比。为了保证筛选出的所有特征指标都有合理的数据，截取2017年11月4日至2018年3月19日期间的数据作为整体数据集；选择2017年11月4日至2018年3月12日期间的特征数据和汽油收率实际值作为训练集，共3096条数据；将其余2018年3月13日到2018年3月19日期间的数据共168条作为测试集，用来验证模型的预测效果和拟合程度。

GBDT算法可以由式(4)来表示。

(4)

其中，T(x，θm)为拟合残差得到的决策树；θm为树的参数；M为迭代次数。对于GBDT算法而言，每一次都在之前建立决策树损失函数的梯度下降方向上建立新的树。即每轮迭代开始时，计算当前损失函数的负梯度的值，并将其作为残差的估计去拟合一个新的回归树。将每轮迭代训练得到的树加权求和，可以得到最终的模型输出。

2.3 GBDT模型效果与分析

通过经验设置与局部网格搜索的方法调整GBDT回归模型的超参数，并对比其交叉验证的结果，根据2.1节中的3个评估标准，可以得到使用该算法进行学习的相对较好的预测模型。真实测量的汽油收率可能出现过大或过小的异常值，采用莱特准则处理异常值之后，绘制实际收率数据的曲线，并对比GBDT模型对催化裂化汽油收率的预测结果，得到工业实际值与预测值的对比曲线如图1所示。由图1可知：模型的预测值总体趋势与工业实际值吻合较好；当实际的汽油收率短时间内波动较大时，模型的预测值与汽油收率实际值之间的偏差较大。

图1 汽油收率预测值与实际值的对比Fig.1 Gasoline yield prediction comparison with actual yield

对于已得到的较优的模型，其评估结果如表1所示。可以看出：GBDT预测模型的准确率达到98.65%，明显高于直接使用均值预测的准确率，验证了该预测模型的可行性和有效性；R2为0.67，表明GBDT模型特征可以有效解释汽油收率的部分变化趋势，且明显优于直接使用均值进行收率预测的效果；汽油收率预测值与实际值的均方根误差为0.80%，相对于均值预测，误差明显降低。计算R2时使用训练集的均值作为数据整体均值，更能反映模型对未来数据的预测能力，同时与直接使用均值预测汽油收率的效果进行对比。由准确率和均方根误差可知，基于GBDT构建的收率预测模型对汽油收率能够起到较为良好的预测效果，得到的预测值与实际值的整体误差较小，但预测所得的R2较小，且无法准确拟合汽油收率中部分变化较大的波动，说明其拟合效果有待提升。

表1 GBDT和均值预测结果Table 1 Results of GBDT model and mean value model

同时，基于GBDT的模型经验可控参数特征的权重较小，部分权重较大的特征为依赖监控的其他特征参数，不利于工业控制中的参数寻优。因此，需要尝试新的寻优方法，对汽油收率预测模型进行改进或优化，尝试使经验可控参数的权重更大，同时提升模型的预测效果和泛化能力。

在实际的工业生产过程中，不同的装置对催化裂化装置产品收率的影响程度不同，整个生产系统对不同装置的偏好也有所不同。因此，在构建算法模型时，模型也应该具备对不同的特征指标具有不同偏好的特性。针对真实数据的状态，笔者提出了基于GBDT的改进算法P-GBDT模型。

3 基于P-GBDT的汽油收率预测

3.1 P-GBDT模型构建

基于GBDT集成学习框架构建P-GBDT算法模型，依据部分特征在实际工艺中的重要性引入特征扰动和特征权重，即采样比率P和特征权重W。引入特征扰动以及依赖权重设置的特征偏向，可保证该类指标在预测模型中的特征重要性更高，并显著增大经验可控指标在模型中训练所得的参数权重。

P-GBDT的基学习器采用与GBDT算法相同的CART分类回归树，将训练中损失函数的负梯度作为树的学习目标。该模型的重要超参数包括模型最大迭代次数、采样比率P和特征权重W，需要在训练前进行人为设定。其中，权重W为由二维数组构成的矩阵，矩阵最大行数表示模型迭代的最大次数，对应列数表示输入数据的特征个数。权重矩阵W的一行表示一次迭代中训练数据的特征权重分布，使不同的特征在迭代采样中根据特征重要性产生对应的采样偏好，同时为模型引入特征扰动。

采样比率P表示对特征进行采样的比例。用一维数组构建模型中每次迭代的样本采样比率。该数组的长度表示模型迭代的次数，其中各数值表示该层模型选取的特征数量占全部特征数的比例。每次迭代开始时，同时依据特征的权重大小和采样比率对特征进行采样。

用T表示训练数据集及模型的输入，其中T={(x1,y1),(x2,y2),……,(xN,yN)},xi∈Rn,yi∈R；模型迭代最大次数M，损失函数为L(y,f(x))，P-GBDT模型的构建过程如3.3节中所示。

3.2 特征分组及权重设置

通过分析操作装置、反应过程以及真实采集数据，结合业务经验和训练特征的实际物理意义，笔者将筛选出的训练特征初步划分为经验可控特征和普通特征两组特征分组。经验可控特征由经业务经验分析或验证的对产品收率有重要影响的特征组成。当该部分特征指标的参数值发生变化时，仅对产品收率值产生影响，不对其他参与训练的特征指标值或整个生产系统产生显著影响。普通特征由其他经Pearson相关性分析和模型筛选得到的特征指标构成，与产品收率存在一定的线性或非线性关系。

依据特征分组对特征权重进行设置，在训练中分别为经验可控特征和普通特征设置一个固定的权重值，且经验特征的权重值大于普通特征的权重值。为经验可控的特征赋予更高的权重，即该组特征在模型的构建过程中重要性更高，可以使其被采样的概率更高，加速模型的收敛；增大经验可控参数的权重，也缓解了GBDT模型对训练特征缺乏偏好的问题。

3.3 实验结果与分析

本次实验所使用的数据集与GBDT模型相同。其中，2017年11月04日至2018年03月12日期间的数据作为训练集；2018年03月13日至2018年03月19日期间的数据作为验证集。构建P-GBDT模型的部分重要训练参数设置如表2所示，并使用以下算法步骤构建P-GBDT模型：

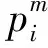
(5)

其中，K为特征总数。

(2)模型初始化：给定训练数据，由此训练出第0颗树，其表达式如式(6)所示。

(6)

其中，f0(x)表示第0棵数；L(·)为损失函数；N为样本个数；yi为第i个样本的汽油收率；c为决策树参数，c0为c的最优值。

(3)对于当前模型迭代次数m，m为1、2、…、M，每次迭代的步骤如下：

(a)对于训练样本i为1、2、…、N，计算损失函数在当前模型的负梯度值rmi：

(7)

(b)根据已知的特征权重和特征采样比率，按照式(5)中的概率对特征进行采样，并作为第m次迭代的训练特征。

(c)对rm拟合一个回归树，训练得到第m棵树。如果该树有J个叶子节点，则第j个叶节点表示为Rmj,j为1、2、…、J。

(d)对j为1、2、…、J，计算线性搜索的最优步长cmj，即参数c的最优值：

(8)

(4)在M次迭代后，得到P-GBDT模型：

(9)

表2中的重要参数主要包括P-GBDT模型特征和样本采样所需参数。将每次迭代的样本采样比例统一设置为0.92，分别设置经验可控特征与其他普通特征的权重均设置为2.0和1.0，通过设置不同的权重从而控制采样概率的差异。使用网格寻优搜索得到其他训练参数的最优取值。对比经过参数调优的P-GBDT模型与基础模型的拟合效果，分别绘制测试集的预测结果如图2所示。

表2 重要训练参数及权重设置Table 2 Typical hyperparameters and weights

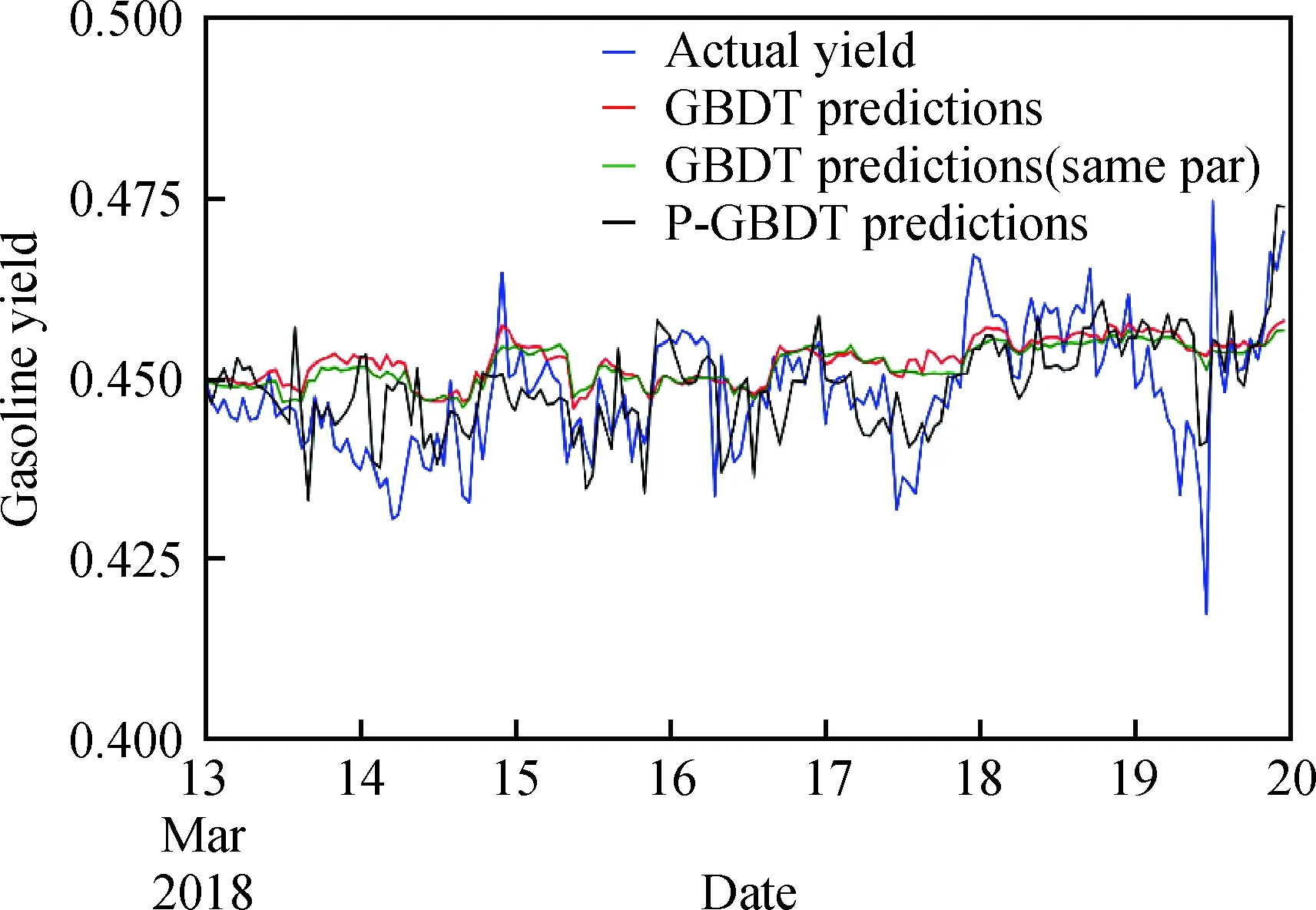
图2 GBDT和P-GBDT模型汽油收率预测对比Fig.2 Gasoline yield prediction of GBDT and P-GBDT models

在相同时间段的测试集上，分别使用P-GBDT模型和GBDT模型对汽油收率进行预测。测试集验证时间较短，汽油收率实际值随着时间的变化相对验证集数据更不稳定，在3月17日至19日之间有明显波折。P-GBDT模型对汽油收率的预测结果在前期有较小偏离，对14日之后的曲线趋势拟合较好，可以真实预测出汽油收率曲线的突变。使用GBDT模型的预测结果相对更为平稳，可以拟合出部分变化趋势较小的汽油收率曲线，但无法对汽油收率的突然变化进行预测。对比2种模型对汽油收率趋势的拟合，基于P-GBDT模型的预测效果显然更优。该模型与其他基础模型在训练集和测试集上的评估标准值如表3所示。

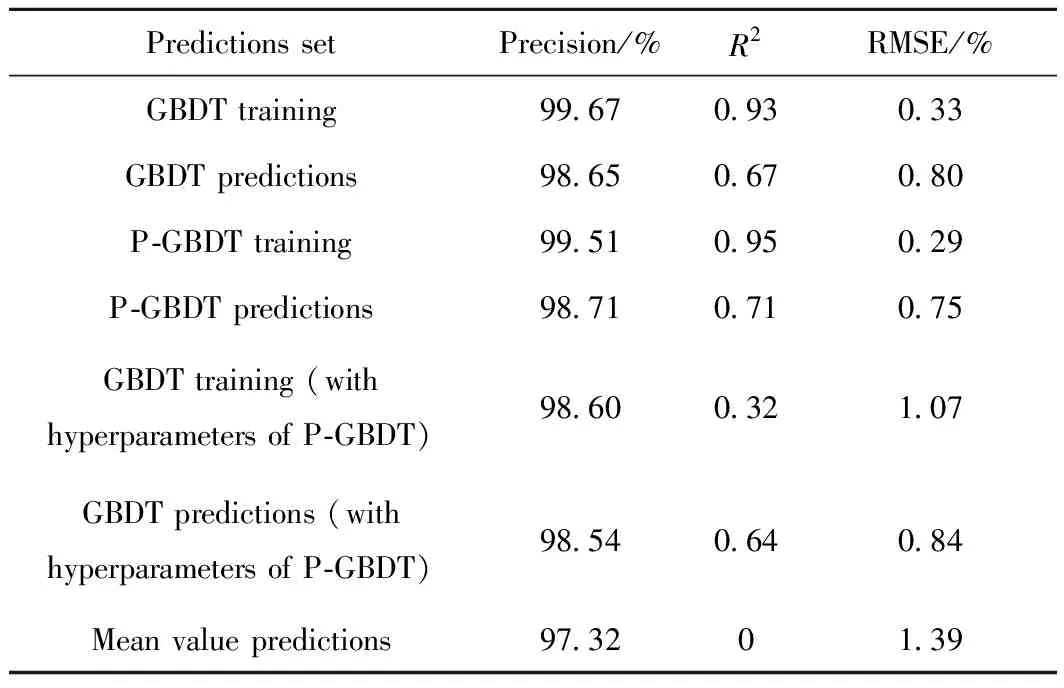
表3 GBDT和P-GBDT回归模型对比结果Table 3 Results of GBDT and P-GBDT regression models

由表3可知，在测试集上P-GBDT的模型准确率相比GBDT提高了0.06百分点，可知P-GBDT在预测准确性上优于GBDT。对于R2而言，P-GBDT 模型测试集的R2值在GBDT模型的基础上提高了0.04，其对汽油收率变化趋势的拟合效果明显优于GBDT模型。此外，GBDT和P-GBDT在测试集上的均方根误差值分别为0.80%和0.75%，误差降低了0.05百分点，表明P-GBDT模型预测的汽油收率与实际值的偏差更小。结合2个模型在测试集上对模型准确率、R2和均方根误差的对比结果可知，P-GBDT模型对汽油收率预测的拟合效果明显优于采用GBDT构建的预测模型。

分别对比2个模型在训练集上和测试集上的表现，P-GBDT和GBDT模型都存在一定程度上的过拟合。但是P-GBDT的过拟合现象明显比GBDT更弱，其训练集上的准确率小于GBDT在训练集上的准确率，R2之间的差值更小。说明P-GBDT改进算法不仅可以提升模型预测的性能，对模型过拟合现象也有一定的缓解。

为了对比相同条件下GBDT与P-GBDT模型的预测效果，利用P-GBDT的决策树深度和最大迭代次数训练对应lightGBM模型，该模型并非使用网格搜索得到的最优模型，因此，其训练效果比原有GBDT参考模型效果更差。使用相同超参数训练GBDT及P-GBDT回归模型的对比评估标准值如表3 所示。

从同参数GBDT模型的训练集表现可以看出，未使用最佳参数时，GBDT模型的表现依然优于直接使用平均值对汽油收率的预测。该模型在训练集上的表现很差，在预测集上反而较好，但预测曲线较为平缓，仅能拟合真实汽油收率的部分波动趋势，依然存在较大的误差。训练集与预测集的差异表明，使用与P-GBDT相同的超参数训练GBDT模型，会出现欠拟合。该模型的表现和P-GBDT模型预测结果的对比如图2所示。

通过分析并对比P-GBDT模型与GBDT参考模型的效果，P-GBDT的各项评估表现明显优于GBDT，且能较好地拟合真实汽油收率的波动趋势，缓解了模型构建中的过拟合。这证明该P-GBDT改进模型是合理可行的，可以提升催化裂化反应中汽油收率的预测性能，并提升经验可控指标在模型中的权重。

4 结 论

基于LIMS及DCS系统中的工业生产数据，通过分析指标与真实汽油收率的相关性，结合工业经验可控参数以及模型重要性筛选、关联指标的剔除，选择了182个潜在影响催化裂化汽油收率的关键参数作为模型的输入特征，并进行进一步的特征处理。利用GBDT算法构建催化裂化汽油收率的预测模型，并将模型对汽油收率的预测效果作为基准值，可以得到以下结论：

(1)基于GBDT集成学习框架构建P-GBDT模型，加入特征扰动和特征权重，并增大经验可控参数的权重。结果发现，由P-GBDT算法构建的汽油收率预测模型预测结果的准确率为98.71%，R2为0.71，均方根误差为0.75%，相比由GBDT算法构建的基准模型的预测结果明显更好，对真实汽油收率的拟合效果更为接近。

(2)通过对比原GBDT模型的预测效果，笔者构建的P-GBDT模型能更为精确地预测催化裂化装置中汽油收率，相比于基础模型的拟合效果更优，针对经验可控的重要指标增大其参数权重，解决了GBDT模型对特征缺乏偏好，经验可控参数特征的权重较小的问题。增大模型中经验可控特征指标的权重，对优化改进实际可控装置操作条件具有良好的指导意义。