振动冲击下PDC切削齿在层理岩层的破岩仿真分析

陈子贺，张玉广，于 涛，李 玮，秦国伟，王旭东

(1. 东北石油大学 石油工程学院，黑龙江 大庆 163318； 2. 大庆油田有限责任公司 采油工程研究院，黑龙江 大庆 163453；3. 大庆钻探工程公司 钻井生产技术服务一公司，黑龙江 大庆 163358； 4. 西安石油大学，陕西 西安 710065；5. 中海油研究总院有限责任公司，北京 100027)

0 前 言

钻井工程中经常钻遇地层倾角大、非均质性强、地层软硬交错富含层理的情况，如北部湾盆地、松辽盆地、川西地区、淮南地区等区域[1-5]，这严重影响了PDC钻头的钻井速度。针对层理岩层发展了不同区域的个性化钻头的设计，但都存在拓展限制大，适应性不高的问题，因此有必要研究PDC钻头在振动冲击作用下的破岩特点。为了提高层理岩层的破岩效率，对于PDC切削齿的破岩机理的研究不容忽视。

国内外学者对于PDC切削齿的破岩机理进行了大量的研究。祝效华[6]基于有限元方法分析了单齿旋冲作用下岩石的裂纹扩展、岩屑形成以及破岩比功等问题。王家骏[7]等使用可以加载钻压的试验设备，在不同钻压、切削面积、切削速度和切削齿后倾角条件下对不同性质的岩石进行钻进试验，建立新的PDC切削齿与岩石相互作用模型。马清明[8]等研究了PDC切削齿的负前角、切削深度等对PDC切削齿和岩石受力的影响作用规律。伍开松[9]等为了观察椭圆形PDC齿的切削效果，用ABAQUS软件模拟椭圆形PDC齿切削岩石的瞬时切削过程，分析椭圆形齿在切削岩石过程中的优势以及破岩效果。Heydarshahy[10]等用有限元法分析了不同PDC切削齿基底与金刚石部分结合界面几何形状对剪切载荷下应力应变分布的影响。Rostamsowlat Ⅰ[11]等通过室内试验研究了后倾角对于破岩效率的影响，研究表明后倾角在5(°)～20(°)之间时有利于破岩，且后倾角超过75(°)后破岩比功急剧增加。

针对目前对于层理岩层研究较少且PDC钻头在该类岩层破岩效率低的问题，本文通过有限元软件建立了PDC切削齿切削层理岩层的数值模拟仿真模型，对比分析了有无振动冲击载荷下的破岩特性以及不同振动频率和冲击幅度对层理岩层破岩效率的影响。研究结果可以对提高钻井工程中遇到的层里岩层破岩效率提供理论指导，最终达到降低钻井成本的目的。

1 模型的建立

1.1 岩石本构模型

Drucker-Prager模型是岩石力学领域常用的岩石本构模型。Drucker-Prager模型不仅能反映中间主应力的影响，也考虑了静水压力对屈服与强度的影响，还可以反映岩石在切削过程中表现出来的失效破坏与流动过程，以及岩石材料的剪胀性影响。因此本文选择该模型用于模拟PDC切削齿的破岩过程。

线性Drucker-Prager模型[12]的屈服面在子午面和π平面的形状如图1所示，屈服函数为：

F=t-ptanβ-d=0

(1)

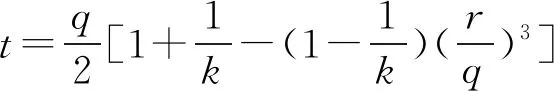
式(1)中：t是另一种形式的偏应力，Mpa；p为等效压应力，MPa；β是屈服面在p～t应力空间上的倾角，与摩擦角φ有关，(°)；d是屈服面在p～t应力空间t轴上的截距，是另一种形式的粘聚力，MPa；k为在三轴试验中，拉伸试验屈服应力与压缩试验屈服应力的比率，如图1所示。曲线a表示k=0.8。

图1 线性Drucker-Prager模型的屈服面

图2 岩石应力与应变关系

1.2 破岩比功模型

为探究PDC切削齿切削层理岩层的破岩特性，本文引入破岩比功的概念。在岩石破碎学中，破岩比功是指破碎单位体积岩石所耗费的能量，破岩比功越低，破岩效率越高。破岩比功为钻齿所做总功与岩石破碎体积的比值，是评价破岩效率的重要指标之一，最早由Teale[13]于1965年提出，即:

(3)

式(3)中：P为破岩比功，mJ/mm3；W为钻齿所做的总功，mJ；V为岩石破碎体积，mm3；FC为钻齿在切向方向受力，N；L为切削行程，mm；S为钻齿与岩石接触面积，mm2。

2 PDC切削齿切削层理岩层仿真模型

大多数的岩石破碎机理研究都定义岩石是各向同性的均质材料，对于层理岩层这种具有强烈各向异性特征的岩石的研究还很少。本文利用有限元仿真软件建立了软硬层理岩层岩石模型。图3为PDC切削齿与层理岩层相互作用模型，岩石的几何模型为长80 mm，宽40 mm，定义该层理岩层岩石模型层理倾角为45(°)，且均匀分布，图中黑色区域为软岩，灰色区域为硬岩，岩石的主要材料参数如表1所示。PDC切削齿齿径为13.5 mm，在其上设置参考点来规定其运动。定义切削齿以1 m/s的速度沿水平方向切削岩石，切削深度为1 mm。本文的切削模型在振动冲击载荷的作用下会给切削齿产生周期性的速度脉冲，定义速度脉冲为1 ms。

图3 PDC切削齿与层理岩层相互作用模型

表1 岩石的材料参数

为验证仿真模型的准确性，进行了相关的常规切削实验。实验设备是动静载荷机械破岩分析系统，如图4所示。通过控制载物台的轴向移动，实现切削实验。图5为实验所使用的层理岩样。将数值模拟仿真得出的PDC切削齿所受切削力与室内试验所得的切削力进行对比。数值模拟仿真得出PDC切削齿上的平均切削力为552 N，室内试验得出PDC切削齿上的平均切削力为532 N，仿真结果误差为3.6%，进而说明了仿真模型的可靠性。

图4 实验装置

3 仿真结果分析

图6给出了无冲击载荷作用时PDC切削齿切削层理岩样与均质岩样切削力的随时间的变化规律。切削层理岩样时平均切削力为518 N，切削硬岩时为534 N，切削软岩岩样时为388 N，切削层理岩层和切削硬岩时的切屑力均值仅相差3.1%，这说明软硬交互界面的存在加大了切削难度。由图6可知：对比PDC切削齿切削均质岩样的切屑力波动曲线，切削均质岩样的切屑力波动较缓，切削层理岩样时切屑力波动较大。下面进行层理岩样在振动冲击作用下的数值模拟仿真分析。

图5 层理岩样

图6 PDC切削齿切削层理岩样与均质岩样的切削力

分析图7所示PDC切削齿切削层理岩层的等效压应力云图，云图中正值表示拉应力，负值表示压应力，从图7中可以看出在切削过程中硬岩比软岩受到更大的压应力，拉应力集中在PDC切削齿与岩石接触的尖端部位，即PDC切削齿挤压岩石的过程中首先在尖端部位形成塑性区和高应力区，之后岩石在达到破坏极限后产生裂纹，裂纹向着切削齿前进方向扩展直至从岩体脱落形成岩屑。

图8所示为有无振动冲击下岩石DUCTCRT(塑性损伤准则)云图，该图展示了不同切削作用下的层理岩层的损伤情况，在图中所圈的部分为PDC切削齿在切削作用下在岩体留下的微裂纹，对比圈1、2与圈1’、2’可以看出，PDC切削齿在振动冲击作用下切削比无振动冲击产生更大的塑性损伤，对于PDC钻头的切削过程，接下来的二次切削更容易产生岩屑，破坏岩体。从从图中箭头所指部分可以看出，同一时刻在无振动冲击时，PDC切削齿下方岩屑堆积较多，不利于破岩，而在振动冲击下岩屑堆积较少，有利于提高破岩效率。

图7 等效压应力云图

图8 有无振动冲击下岩石DUCTCRT(塑性损伤准则)云图

图9为固定冲击幅值0.1时(幅值0.1表示增加原冲击幅度的10%)，改变振动频率所得的平均切削力和破岩比功与无振动冲击载荷的所得的平均切削力和破岩比功的对比示意图，无振动冲击载荷即常规切削时的破岩比功为363.53 N/mm2，不同振动频率下的破岩比功依次为341.91，334.36，329.57，324.12 N/mm2，频率越高，破岩比功越低。图10为固定振动频率为1次，改变冲击幅值所得的切削力和破岩比功与无振动冲击载荷的所得的切削力和破岩比功的对比示意图，不同冲击幅度下的破岩比功依次为341.91，335.69，338.61，336.41 N/mm2，破岩比功与冲击幅值无明显相关性，幅值0.2时破岩比功最低。综上数据可以看出：在层理岩层，PDC切削齿在振动冲击载荷作用下的破岩比功均低于无振动冲击载荷的破岩比功。从图9、10可以看出破岩比功与切削力呈正相关。

图9 不同振动频率下的切削力与破岩比功

图10 不同冲击幅度下的切削力与破岩比功

4 结 论

用有限元软件建立PDC切削齿在振动冲击下破碎层理岩层的仿真模型，研究了层理岩层在PDC切削齿切削过程中的破碎情况，以及不同振动频率和冲击幅度对层理岩层破岩效率的影响。

1)在切削过程中硬岩比软岩受到更大的压应力，拉应力集中在PDC切削齿与岩石接触的尖端部位，即PDC切削齿挤压岩石的过程中首先在尖端部位形成塑性区和高应力区，之后岩石在达到破坏极限后产生裂纹，裂纹向着切削齿前进方向扩展直至从岩体脱落形成岩屑。

2)PDC切削齿在振动冲击作用下切削比无振动冲击产生更大的塑性所伤，同一时刻在无振动冲击时，PDC切削齿下方岩屑堆积较多，不利于破岩，而在振动冲击下岩屑堆积较少。

3)对于PDC切削齿切削层理岩层，振动频率越高，破岩比功越小，冲击幅值大小与破岩比功无明显相关性，破岩比功均小于无振动冲击载荷时的破岩比功。振动冲击载荷有利于提高层理岩层的破岩效率。