铝合金材料激光冲击喷丸力学响应有限元建模*

舒波超，李卫东，黄 遐，车志刚

（1.北京航空航天大学机械工程及自动化工程学院,北京 100191；2.中国航空制造技术研究院,北京 100024）

激光冲击喷丸利用高能脉冲束产生的冲击力在材料表层引入局部塑性应变，诱导产生有益的残余压应力场，在飞机和发动机关键部位疲劳增寿等领域具有广阔的应用前景。激光冲击喷丸时，激光透过约束层辐照材料表面的吸收层，吸收层迅速气化形成等离子体，等离子体气团在约束层限制下产生局部爆炸，形成爆炸冲击波。当冲击波压力大于材料的雨贡纽（Hugoniot）极限时，材料发生屈服从而产生塑性变形，并产生残余压应力。研究表明，与无约束层相比作用时间延长2～3 倍，冲击波压力提高7 倍左右[1]。

激光冲击喷丸受到了国内外学者的广泛关注。早在1961年，国外科学家就已发现激光诱导等离子体冲击波的现象。Dawson 在1964年提出激光诱导产生的等离子是材料蒸汽的电离结果[2]。在20 世纪70年代，Fairand 等[3]利用高功率激光辐照7075 铝合金改善了其机械性能，微观组织得到细化。在20 世纪90年代，美国激光冲击技术公司（LSPT）利用激光冲击喷丸强化技术为GE 制造了应用于罗克韦尔B–1 Lancer 轰炸机装配的F101 发动机风扇叶片生产线[4]，开始从实验室迈进工业化应用。在国内，Cui 等[5]研究了激光冲击波驱动纳米粒子注入（LSWNI）作为塑性变形中新的表面强化技术，研究发现材料的力学特性、微观结构等得到大幅改善。空军工程大学与多方合作，组建了国内第一条激光冲击喷丸强化生产线，紧跟美国成为全球第二个利用该技术实现工业生产的国家。

在数值模拟研究方面，Zabeen等[6]通过有限元仿真比较不同屈服强度下的残余应力分布，分析认为材料高屈服强度导致塑性变形的抵抗增强，因此残余应力在低屈服应力下深度较大。Ocaña 等[7–8]利用自主开发的计算模型分析了激光冲击波产生和传播问题。Brockman 等[9]着重研究了激光冲击区域内应力的时间变化，表明板材背面的反射波阻止了深度方向的塑性流动。张兴权等[10]建立了激光诱导残余应力模型，并提出激光功率密度对残余应力的影响规律。

在现有研究中，冲击力的加载主要是利用Fabbro 理论模型，或者根据试验测量的应力应变反向求解激光冲击力，模拟精度不高，操作灵活性较差，且无法准确获取冲击力随时空分布的特性曲线。激光冲击喷丸的应变率在105～106s–1之间，Johnson–Cook 本构模型是否适用于该超高应变率的一维应变状态还有待验证。而冲击力学加载与材料本构模型是有限元建模的关键步骤，对最终计算结果的精度有较大影响。

因此，本文针对航空铝合金材料2024–T351，结合理论推导、试验测试与有限元分析，采用PVDF 压电传感器测量并构建了激光冲击力加载模型，利用轻气炮试验验证了Johnson–Cook 本构模型及参数，在此基础上建立了激光冲击喷丸有限元模型，并利用数值模拟及二次开发实现了数据快速分析及试验验证，研究了激光冲击喷丸中材料动态力学特性及残余应力分布规律。

激光喷丸冲击力测量与模型构建

利用PVDF 压电传感器测量强激光诱导冲击波压力，并由Tektronix DPO4104 高精密数字示波器采集电压信号，通过数据处理得出冲击载荷随时空分布的波形曲线，试验装置如图1 所示。

当高能脉冲束冲击金属板材时，根据PVDF 传感器的压电效应可知，表面压力大于背面时释放正电压，相反产生负电压。对电压波形进行积分，可由式（1）求得传感器产生的电荷—时间关系曲线[11]：

式中，Q为传感器产生的电荷，R为回路积分电阻，U（t）为t时刻所测电压信号，I（t）为t时刻回路电流。

激光诱导冲击波压力与压电传感器产生电荷量Q之间的关系可由式（2）计算求得，根据公式可以得出冲击力随时间的动态加载特性曲线。

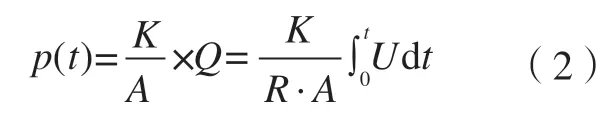
式中，p（t）为t时刻激光冲击波压力，K表示PVDF 压电薄膜的动态灵敏系数，A表示压电薄膜的有效工作面积。

激光冲击波在空间的分布特性已有广泛而深入的研究，普遍认为激光强度在空间上符合非均匀准高斯分布，在距中心 2R时强度减小至I0/e2，其分布函数可由式（3）计算求得。

式中，e为激光强度，x、y为冲击区域内某点的坐标值，R为光斑半径。

激光发射源采用Nd：YAG 脉冲激光器，激光光斑为4mm×4mm 的方形光斑，波长为1064nm，频率为1Hz，脉宽为15ns。试验激光能量分别为20J、25J 和30J，利用示波器测量不同能量下的激光冲击力。选取重复率较高的试验数据作为最终测量结果，图2 所示为数据处理之后的压力波形曲线，其中激光冲击波峰值压力分别为2.74GPa、3.17GPa 和3.88GPa，峰值压力随激光能量的增大而增大。

将试验结果与Fabbro 等[12]的理论推导作对比，其理论估算的简化形式为：

式中，Pmax为冲击波峰值压力；α为内能转化系数，常取0.2；Z为约束层与靶材的声阻抗；I0为激光功率密度。本试验采用水膜作为约束层，可得激光诱导冲击波峰值压力的试验测量值与理论模型数值对比如表1所示。

图1 激光冲击力测量装置图Fig.1 Laser impact force measuring device

图2 激光冲击力数据处理Fig.2 Date processing of laser impact force

大量试验结果表明，该理论计算模型误差较大，在数值上比实测值高出很多，分析原因为：（1）该模型忽略了等离子体在靶材、能量吸收层与约束层之间的相互作用；（2）忽略了冲击波压力在靶材中的衰减效应；（3）激光诱导冲击波的传播方向并不局限在一维径向传播；（4）靶材和约束层的声阻抗在高温下不是常数。因此，可以认为试验测量结果较为准确。

以E=30J 为例分析试验结果，选取拟合精度较高的Fourier 函数将压力波形曲线进行数值拟合，级数设置为3，可以得出冲击力随时间分布的加载模型，其拟合公式为：

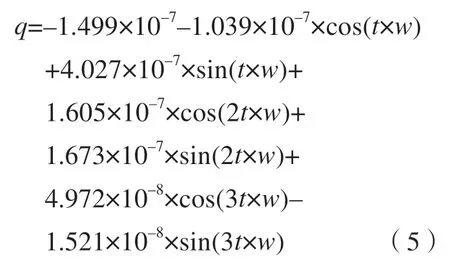
式中，w=0.01572，t∈[0，150]ns。

超高应变速率本构模型构建

激光冲击喷丸的应变率在105～106s–1之间，Johnson–Cook（J–C）本构模型在工程应用及模拟仿真中应用最为广泛，其应力–应变关系由式（6）求得，材料参数见表2[13]，假设材料为各向同性。

式中，σ表示材料的流动应力，ε表示等效塑性应变，ε˙0 代表参考应变率，A、B、n、C、m为材料参数，Tr代表参考温度，取值为293K，Tm代表材料熔点。因激光冲击喷丸忽略温度影响，可将模型最后一项省略。

表1 激光冲击力试验测量值与理论模型数值对比Table 1 Comparison of experimental measurements with theoretical models

表2 铝合金2024–T351的Johnson-Cook模型常数Table 2 Material parameters of aluminum alloy 2024-T351 in Johnson-Cook model

然而J–C模型由一维应力试验Hoplinson 拉伸标定，应变率在1×104s–1以下，其是否适用于更高应变率下的一维应变状态鲜有报道[14]。因此本文利用轻气炮试验，对AA2024–T351开展平板撞击试验，以构建更高应变速率下的本构模型或验证J–C 模型的准确性，试验装置如图3 所示。

利用有限元软件ABAQUS 和J–C 本构模型及其常数，对上述的轻气炮撞击试验进行数值模拟，仿真中不考虑层裂破坏效应。图4 所示为3 组试验中自由面介质粒子速度仿真与试验对比，冲击力为方波加载。对比结果表明，仿真能较好地预测试验现象，表明J–C 本构模型及其常数适用于应变率在105～106s–1之间的一维应变状态，而激光冲击喷丸属于只受轴向应变的一维应变状态，且应变速率与该平板撞击试验非常接近，可知激光冲击喷丸与轻气炮的应力应变关系较为一致，因此J–C 本构模型可以应用到激光冲击喷丸中。因此，下文将利用该模型开展激光冲击喷丸数值模拟研究。

激光冲击喷丸有限元建模

图3 轻气炮试验装置示意图Fig.3 Light gas gun experimental device schematic

激光诱导等离子冲击波作用到板材表面后，表层质点由外向内相继发生位移，从而产生应力波。在板材内部，由于强冲击波、稀疏波及界面反射后的拉伸波等关系错综复杂，考虑将激光冲击波等效为压力载荷作用到板材表面上，利用ABAQUS 软件中VDLOAD 子程序接口，将冲击力模型参数化，通过编程改变激光冲击喷丸工艺路径，实现单点、多点及不同覆盖率的精确冲击并节省计算时间。

在进行激光冲击喷丸数值模拟时，一般认为模型尺寸需要扩展至光斑半径的1.25 倍以上。在激光方形光斑4mm×4mm 条件下，建模所用尺寸为10mm×10mm×10mm。为保证材料塑性变形、残余应力等力学响应稳定，经过研究表明，动态求解时间ABAQUS/Explicit 至少是冲击波脉宽的两个数量级[15]，因此动态求解时间最终确定为2×105s。

网格密度与模型计算结果的准确性密切相关，选择合适的网格尺寸能有效提高计算效率，并保证合理的计算精度。以时间为2×105s 时冲击表面中心的Mises 应力作为判断指标，在各向同性材料假设下，x、y方向的网格尺寸保持一致。从图5 中可以看出，Mises 应力逐渐收敛为固定值，因此选取图5（a）中z方向网格尺寸为H=0.05mm，选取图5（b）中x、y方向的网格尺寸为Lx=Ly=0.1mm，其中N代表网格总数。

图4 不同应变率下介质粒子速度仿真与试验对比Fig.4 Simulation and experimental comparison of medium particle velocity at different strain rates

激光冲击喷丸模拟与验证

激光冲击波加载到板材表面后，会在板材表层与深度方向产生不同的力学响应。在冲击平面内将形成一定深度的凹坑，冲击波到达凹坑边缘后发生发射，并在冲击区域中心汇聚产生拉伸稀疏波，抵消部分压应力或直接在表面产生残余拉应力，大量研究发现板材表层的残余压应力并非最大值，该结论充分验证了这一假设。冲击表面处的应力较复杂，其Von Mises 力学响应随时间的变化如图6 所示。

在深度方向上，应力波以指数衰减规律传播，且压应力波和拉应力波分别向底部运动，拉应力波包括冲击平面内的稀疏波、板材后表面的反射波等。图7 所示为400ns 时的应力传播示意图，应力波在其内部相互作用，在整体上形成较为复杂的应力状态。这些现象在试验中无法观察，需要借助有限元模拟软件ABAQUS 加以分析，它在研究高速率动态爆炸冲击方面发挥了关键作用，并且可以重复观察高成本的试验现象。

在冲击区域中心单元的不同深度上，激光冲击波压力随传播距离而衰减，其衰减示意图如图8 所示。可知，冲击区域表面的力学响应等同于试验所测冲击力。距冲击表面越远，峰值压力越小，且峰值到达时间延迟。由于材料固有黏性、熵增等引起的能量损耗，冲击波与材料不断发生交互作用，研究表明其衰减规律呈指数形式减小[16–17]。

图9 所示为激光冲击喷丸结构件的等效塑性变形示意图。可知，塑性应变基本位于方形光斑范围内，在空间上符合高斯分布，在冲击区域中心达到最大值。在冲击波压力加载结束即150ns 之后，冲击表面不再发生塑性应变，只在深度方向上随冲击波的传播相继发生变形，但由于应力波的衰减塑性应变的幅值减小。当应力衰减到小于雨贡纽（Hugoniot）极限时，塑性应变的深度达到最大值。

为验证有限元模型对材料动态力学特性预测的准确度，进行了残余应力测试，检测系统如图10 所示，该装置是由StressTech 公司设计的PRISM 残余应力检测系统。该系统配合增量钻孔法和电子散斑干涉（Electronic Speckle Pattern Interferometry）技术，钻孔深度分别为0.02mm、0.05mm、0.1mm、0.2mm、0.25mm、0.3mm、0.4mm 和0.5mm，在近表面处残余应力梯度较大，因此需要较小的进给深度以获得准确的测量结果。

利用ABAQUS 软件的Python二次开发接口，编写程序提取不同深度和径向方向的残余应力分布，提取范围在径向上等同于钻头直径，在深度上随钻孔深度的改变而变化，通过一定区域的平均值减小了单元或节点数值带来的误差。

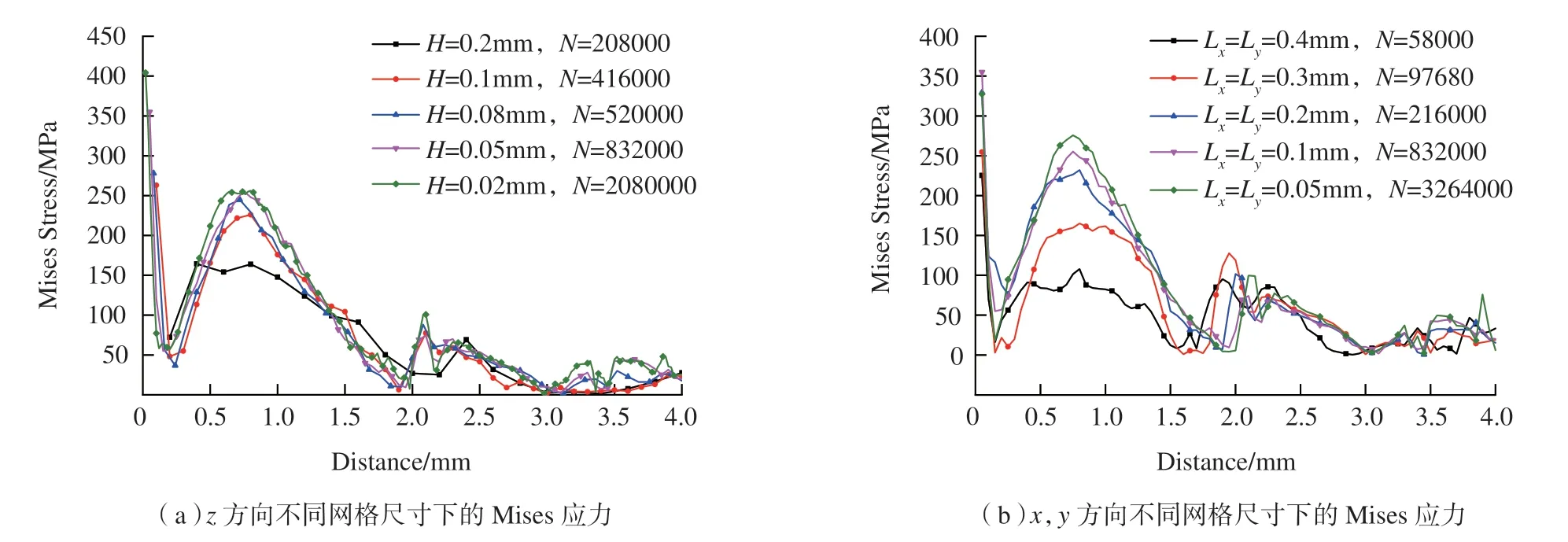
图5 网格灵敏度分析Fig.5 Grid sensitivity analysis

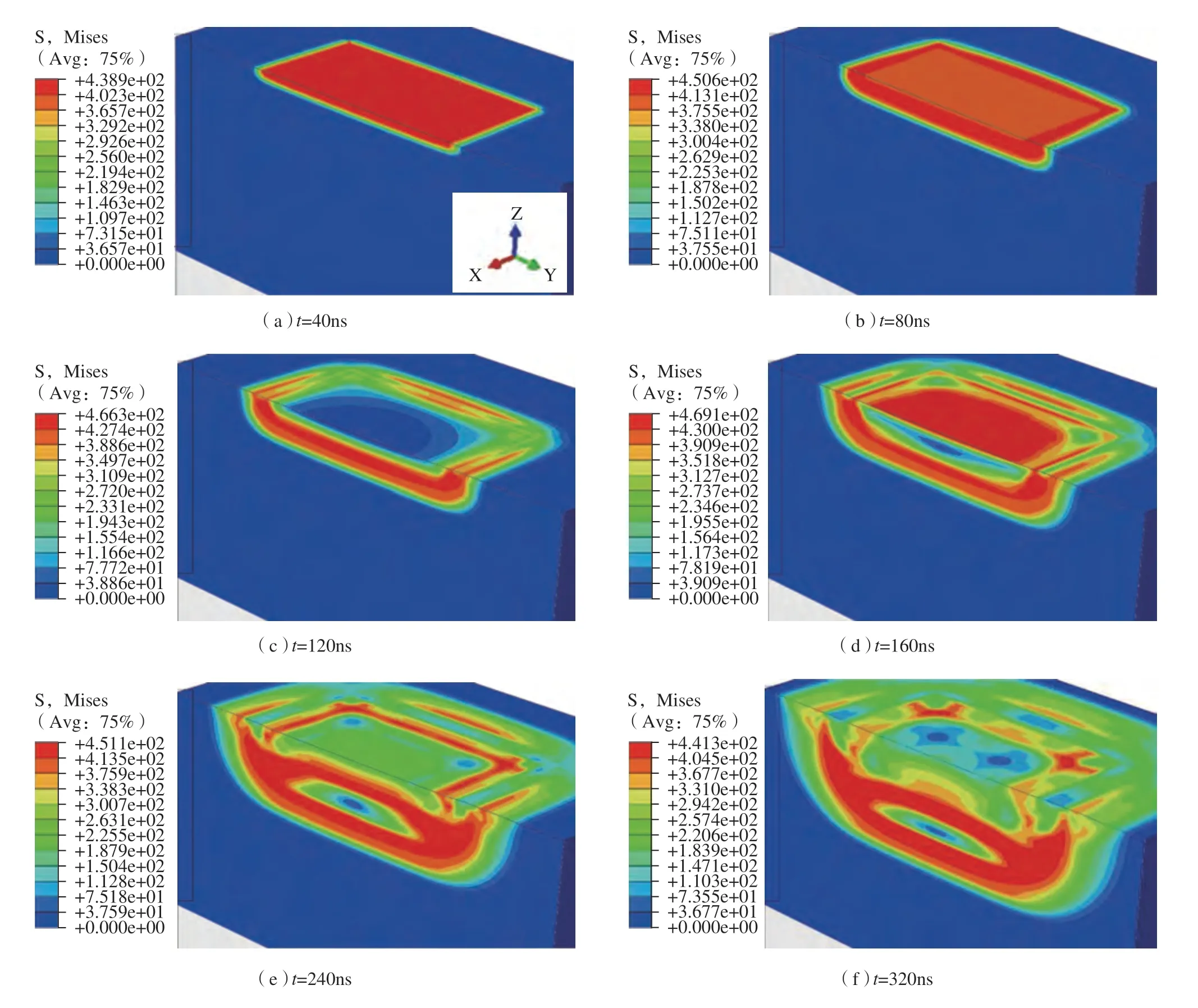
图6 Von Mises应力响应示意图Fig.6 Schematic diagram of Von Mises stress response

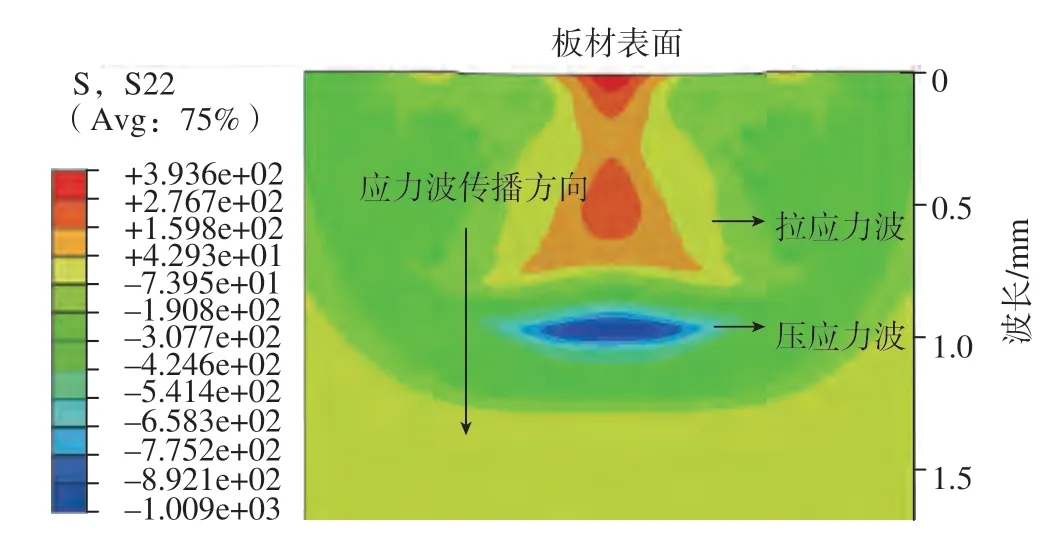
图7 400ns时应力波传播示意图Fig.7 Schematic diagram of stress wave propagation at 400ns

图8 不同深度的激光冲击波压力Fig.8 Laser shock wave pressure at different depths

图9 不同时间段的等效塑性应变Fig.9 Equivalent plastic strain at different time periods

图11对比了t=10mm、E=30J时0.2mm 深度以内单点1 次到3 次冲击的残余应力仿真与试验检测结果。永久塑性应变将导致板材内部产生残余压应力，单点重复冲击会使塑性应变进一步增大，残余压应力的幅值与深度随之增加。在激光冲击3 次、深度0.2mm 时存在最大误差102MPa，此处钻孔深度较大，应力释放较显著，其余状态下误差较小，且残余应力场的分布都符合相同趋势，残余应力有限元模拟结果与测量结果吻合较好，因此有限元仿真能够较好地预测残余应力场的分布规律。

图10 基于钻孔法的PRISM残余应力测试系统Fig.10 PRISM residual stress testing system based on drilling method

图11 0.2mm以内单点多次冲击仿真与试验测量对比Fig.11 Comparison of single point multiple impact simulation and test measurement within 0.2mm

结论

本文通过理论分析与试验，针对铝合金2024–T351 材料，建立了激光冲击喷丸有限元模型，并进行了残余应力测试验证，得到的结论如下：

（1）利用PVDF 压电传感器和高精密数字示波器测量了激光冲击力数据，建立冲击力时空分布的动态压力模型，并在ABAQUS 软件中使用VDLOAD 子程序实现了动态力学加载。与传统的R.Fabbro 理论力加载模型对比，试验测量获得激光冲击喷丸力加载模型更为准确。

（2）利用轻气炮加载技术开展了一维平板撞击试验和有限元仿真。有限元仿真与试验对比表明自由面介质粒子速度一致性较好，验证了Johnson–Cook 本构模型及其常数可以应用到超高应变率下的激光冲击喷丸有限元仿真。

（3）进行了一定工艺参数下激光冲击喷丸有限元模拟，利用Python二次开发，提取冲击区域内的残余应力分布，并与表面残余应力试验测量结果进行对比。残余应力有限元模拟结果与测量结果吻合较好，从而验证了建立的激光冲击喷丸有限元模型的准确性。