考虑供热系统热储能特性的电-热综合系统随机优化调度模型研究

周 丹，孙 可，郑朝明，陈锡祥，郑伟民

（1.浙江工业大学 信息工程学院，浙江 杭州 310023；2.国网浙江省电力有限公司，浙江 杭州 310007）

0 引言

能源是人类生存和发展的基础。随着人类社会的不断发展，能源危机日益凸显，危及人类社会的持续发展[1]。以能源互联网为核心的第三次工业革命正在不断兴起，为多种能源间的协调互补和梯级利用提供可能性[2]，[3]。综合能源系统（Integrated Energy System，IES）作为能源互联网的一种重要形式，具有重要的研究意义[4]。此外，可再生能源渗透率的不断增加及其出力的随机性，给综合能源系统的运行带来了极大的挑战[5]。考虑风电出力随机性的综合能源系统协同运行已成为该领域的研究热点。

热能具有传输损耗大、可有效存储的特性，与电能形成天然互补，因此，电-热综合能源系统已经成为研究热点[6]～[9]。文献[6]采用自适应实值编码遗传算法对含热电联产机组的电-热综合能源系统进行调度分析。文献[7]采用蜂群优化算法，以电-热综合能源系统总运行成本最低为目标，寻找热电联产机组最优运行点。文献[8]和文献[9]分别通过配置储热装置和电锅炉装置来提升热电联产机组的调节能力。以上文献均以电力系统为主体，仅考虑分析了电、热系统间的相互影响制约关系，对热力系统只考虑了热力平衡这一约束条件，并未在模型中考虑热力网络约束条件的影响。

热力系统通常可分为一次管网和二次管网，中间以换热站作为连接，热力系统网络通常可被看作为一个流体网络，即把供热管道看作支路，把热源、热交换站和热负荷看作节点，从而构成有向拓扑结构图[10]，[11]。此外，文献[12]从能量流出发，分析了热力系统中基本元件的热量传递过程，提出了一种电-热综合能源系统的优化模型。文献[13]从稳态角度推导了热力系统中能量的传递方程式和网络方程。但是，上述文献只描述了电-热综合系统间的静态转换关系，忽略了热力系统中存在的热惯性动态特性。

文献[14]通过实验，证明了供热系统中的热源供热量在十几到几十分钟的时间尺度内波动，不会对用热负荷造成可察觉的影响。文献[15]在模型中考虑了集中供热系统的蓄热特性，建立了热电联产机组的多时间尺度调度模型。文献[16]分析了供热系统的输送容量、输送延时、输送损耗等条件对电-热能源集成系统运行结果的影响，同时分析了不同运行方式对风电消纳的影响。文献[17]针对供热系统中的响应特性，提出了多时间尺度下的协调模型。以上文献均考虑了热力系统的动态特性及其在电-热系统优化调度中所起到的作用。然而，风电等可再生能源具有随机性和出力不确定性，对电-热综合能源系统运行产生的影响是不可忽略的。

针对上述研究存在的问题，本文采用随机优化方法对电-热综合能源系统所包含的风电随机性进行描述，采用基于多场景的方法模拟风电不确定性，构建了优化调度模型。首先，对供热系统的热源、热交换站节点和一次管网进行了数学建模，分析了供热系统的热传输延时和热损耗等动态特性；其次，给出了电-热综合能源系统的基本结构图，搭建了包含风电不确定性的电-热综合能源系统优化调度模型，模型以综合能源系统总购能成本最低为目标函数，以电力系统网络约束、热力系统网络约束和耦合装置运行约束为约束条件；最后，在IEEE33节点和6节点热力系统上进行了算例分析，在分时电价环境下，分析了供热系统热储能特性，并验证了模型的有效性。

1 供热系统建模

供热系统一般由供热源、热能传输管道、热交换站和热负荷组成。供热系统又可以分为一次管网和二次管网（图1）。热交换站在一次管网中相当于负荷，在二次管网中相当于热源，一次管网和二次管网通过热交换站实现热量交换。

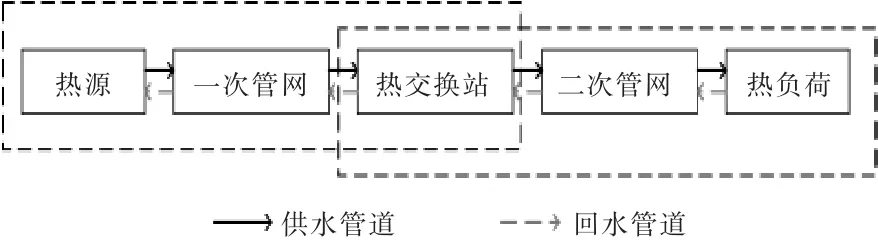
图1 供热系统基本结构图Fig.1 Basic structure of the thermal system

由于供热网的热延时性主要体现在一次管网中，故在本文的电-热综合能源系统中，主要考虑一次管网，即考虑将热交换站作为负荷分析。热能传输管道通常包含供水管网管道和回水管网管道，传热介质通过供热管网将热量传输给热负荷，然后通过回水管道回到热源处，重新获得热量，从而形成循环。

1.1 热源与热交换站节点模型

在供热系统中，在t时刻热源节点i供应热量为QiRY（t），将回水管道中流回质量流量为qiRY（t）的介质从回水温度 Tiret（t）提升至供水温度然后通过供水管道流出，供应下一阶段的热量需求：

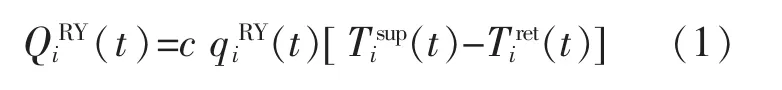
式中：c为水的比热容，c=4.2 kJ/（kg·℃）。

在一次管网中，热交换站相当于热负荷，在t时刻节点i消耗从供水管道流出的热量使质量流量为的传热介质温度从供水温度降低为回水温度：

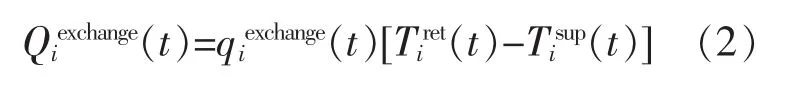
在二次管网中，热交换站与用户热负荷间须满足能量守恒：

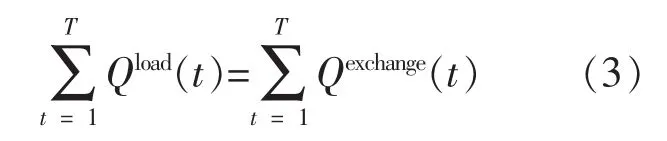
式中：Qload（t）为 t时段的计算热负荷，kW；T为调度时间。

1.2 一次热网模型

供热系统一次网络中通常可以用节点质量守恒方程、节点温度混合方程、供热管道运输准动态方程和供水、回水温度约束条件进行描述。

（1）节点质量守恒方程

在一次热网中的每个节点的流入、流出质量须保持不变：

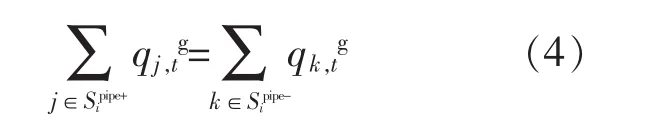
（2）节点温度混合方程

实际上每根供热管道中的热水温度都不相同，不同温度的热水汇入到一个节点，混合后的节点温度为

式中：Tj，tOUT为第t时段管道j出口的混合热水温度；Tk，tIN为第t时段汇入管道k中的热水温度。

（3）供热管道运输准动态方程

在供热管道中，由于热水水温变化缓慢，从入口处流入热水的温度变化将会缓慢地拓展到出口处，具有一定的传输时延。同时，由于供热管道与周围环境温度存在差异，热水会在流动过程中产生热量损失。因此，本文借鉴文献[18]的供热延时处理方法，通过传输时延τ和管道入口处水温历史数据的时间序列，结合传输过程中产生的热量损失，计算管道出口处的水温。该计算程序是先在不考虑热量损耗的情况下，计算管道出口温度；再在考虑管道热量损失下，计算管道出口温度。

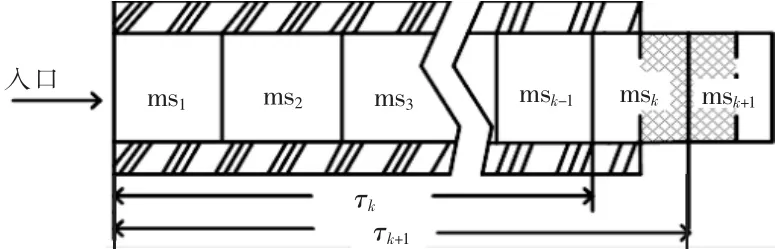
图2 供热管道截面图Fig.2 Vertical section of the thermal pipeline

如图2所示，在一根长为lj的供热管道j中，假定将调度周期T平均划分为N个Δt部分，每个部分的质量流量为ms。在阴影部分，其传输延时介于τk和τk+1之间，其质量流量由msk和msk+1中各取一部分组成，因此管道出口处水温可由阴影部分的Δms1和Δms2的加权平均值表示：

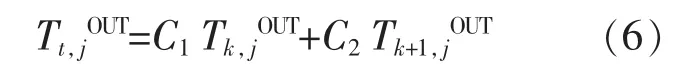
式中：C1，C2为权重系数，本文 C1，C2均选取值为0.5。

由于具有时延效应，msk处流入管道的水温应该是在t-τk时刻管道入口处的水温；msk+1处流入管道的温度应该是在t-τk+1时刻管道入口处的水温。

由于管道与周围环境温差而产生的管道传输热量损失：

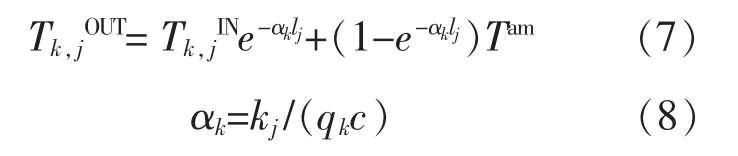
式中：kj为管道漏热损失系数，W/（m·℃）；Tam为管道周围环境温度，℃。

考虑时延效应，可将式（7）修改为

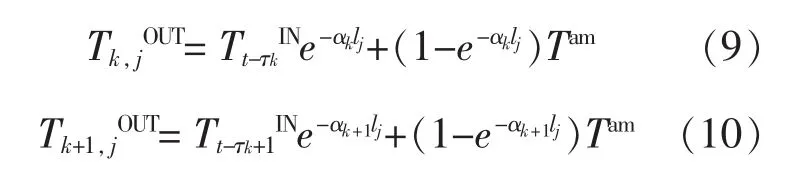
将上述两式带入式（6），可得考虑热损失和传输时延下的管道出口处温度方程式。

从供热管道运输准动态方程式的分析可以看出，由于考虑了传输时延，管道入口处和出口处的介质热量在同一时刻并不相等，这种特性与储能元件相似，故相关研究将此种特性称之为虚拟热储能动态特性。

（4）供、回水温度约束

为了使供热网络能够保持一定供热效果，管道的供水温度和回水温度都须保持在一定限制内，即：

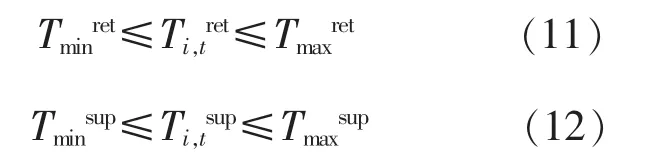
2 考虑热储能下的电-热综合系统调度模型

2.1 电-热综合系统基本结构

电力系统传输快、不易存储，热力系统传输消耗大、可有效存储，这两种能源可有效互补。图3为电-热综合能源系统的基本结构图。电-热综合能源系统主要包括配电网、风电机组、热电联产机组、热泵等单元，各单元通过热电联产机组和热泵设备耦合。

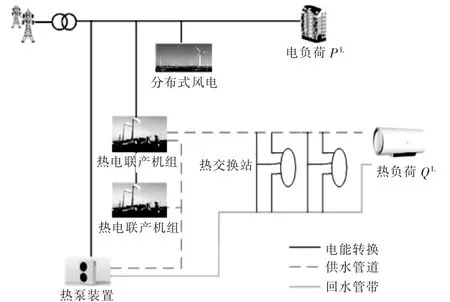
图3 电-热综合能源系统基本结构图Fig.3 Structure of integrated electricity-heat system

2.2 多场景法

风电具有出力不确定性，对电-热综合能源系统的调度将产生影响。本文采用多场景法处理风电不确定性，通过可能出现的风电出力场景进行模拟，将不确定性因素转化为多个确定性场景问题。

本文假定风电出力波动满足正态分布，采用蒙特卡洛法生产大量样本场景，模拟风电出力的可能状态。采用K-means聚类算法将产生的大量风电出力样本场景削减成S个，以降低计算量，削减后获得每个典型场景的概率分布为{ps}[19]。

2.3 目标函数

考虑热储能特性的电-热综合系统优化调度的运行成本包括从上游电网购电费用、天然气购买费用和弃风成本：

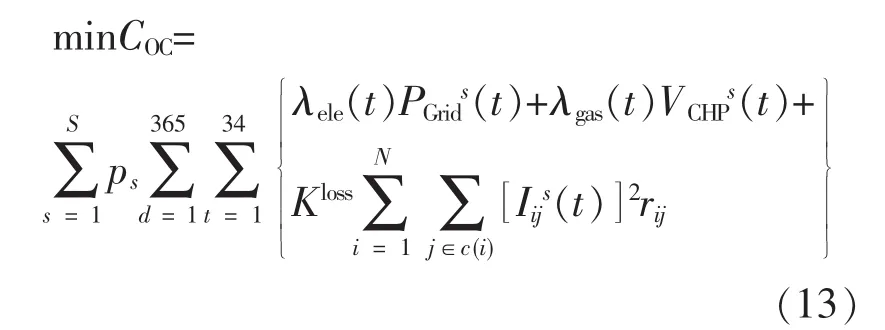
式中：λele（t）为 t时刻主网的分时电价，元/（kW·h）；λgas（t）为 t时刻购买天然气的价格，元/m3； PGrids（t）为t时刻在s场景下区域综合能源系统向主网购买的电量，kW，PGrids（t）为正时表示向主网购买电量，PGrids（t）为负时表示向主网销售电量；VCHPs（t）为t时刻在s场景下热电联产机组的天然气消耗量，m3；N为总节点数；Kloss为网损电价；c（i）为所有以i为首端节点的末端节点集合；Iijs（t）为支路ij在 t时刻s场景下流过的电流；rij为支路ij的电阻。

2.4 约束条件

考虑热储能特性的电-热综合系统优化调度模型约束条件包括电功率平衡约束、电网潮流约束、热功率平衡约束、热电联产机组约束和热泵装置约束。

（1）电功率平衡约束

电力系统侧的有功输出和有功需求须满足供需平衡，即：

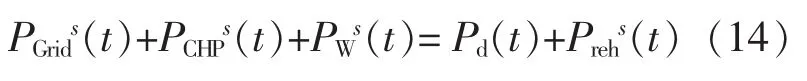
式中：PCHPs（t）为t时刻在s场景下热电联产机组发出的有功功率；Pd（t）为 t时刻有功负荷；Prehs（t）为t时刻s场景下热泵装置的电功率。

（2）电网潮流约束

δ（j）是以j为首端节点的支路末端节点集合，π（j）是以j为末端节点的支路首端节点集合：

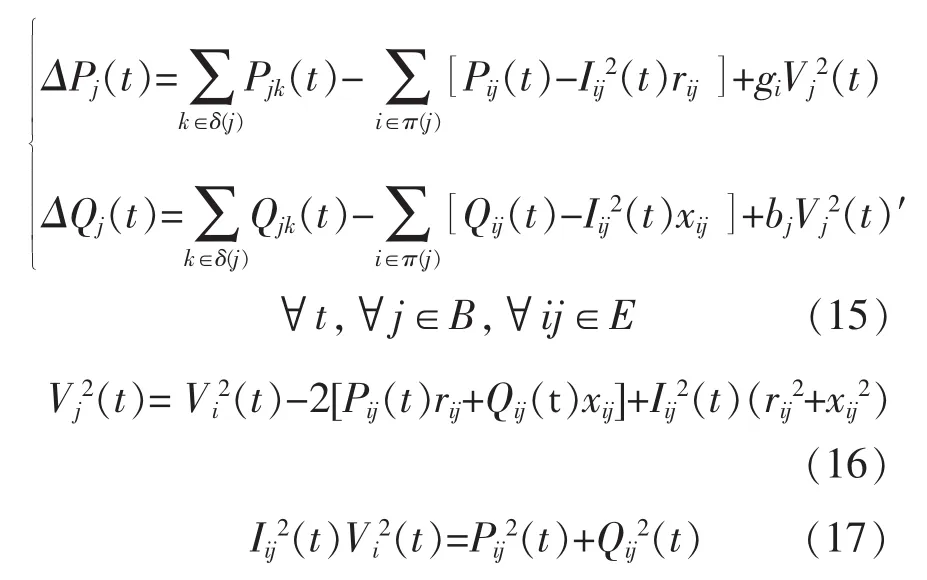
式中：rij，xij为节点阻抗矩阵；Pjk，t，Qjk，t为 t时刻节点 j的流出功率；Pij，t，Qij，t为 t时刻节点 j的流入功率；B为网络中所有节点集合；E为网络中所有支路集合；ΔPj，t，ΔQj，t为 t时刻节点 j的净注入功率。

（3）热功率平衡约束

热力系统侧的热出力和热负荷须满足能量守恒，即：

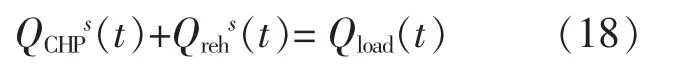
式中：QCHPs（t），Qrehs（t）分别为 t时刻 s 场景下热电联产机组和热泵装置的热出力，kW。

（4）热电联产机组约束

热电联产机组是消耗天然气同时产生电、热的设备，是电力系统和热力系统间的耦合装置。假设本文热电联产机组为背压式，其热、电出力满足一定的正比例变化，如式（19），（20）所示。式（21）表示热电联产机组的出力约束；式（22）表示机组的爬坡约束。

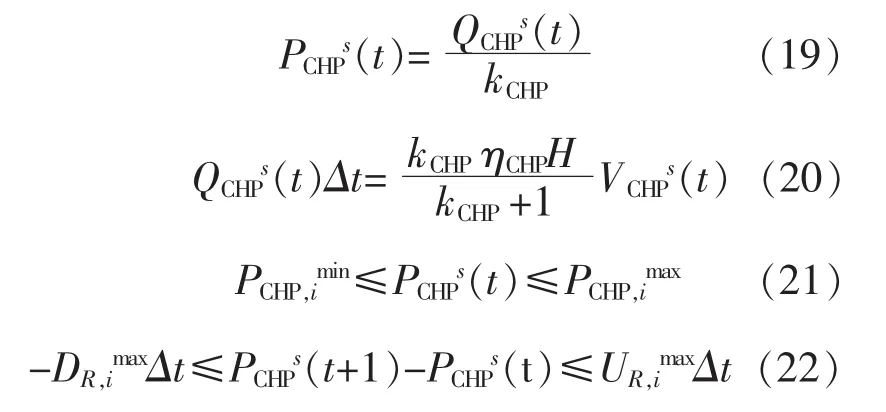
式中：kCHP为热电联产机组的热电比，取1.11；ηCHP为热电联产机组的效率，取0.69；H为天然气的高热值，取 9.88 kW·h/m3；PCHP，imax，PCHP，imin分别为热电联产机组出力约束的上、下限；UR，imax，DR，imax分别为最大上调、下调功率。

（5）热泵装置约束

热泵装置是消耗电能产生热能的装备，其消耗电功率和热出力须满足式（23），（24）：

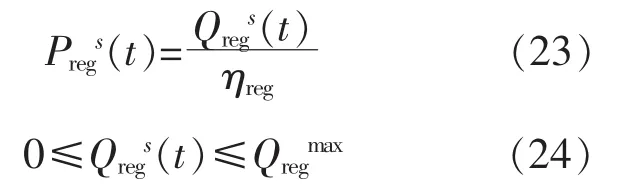
式中：ηreg为热泵电热转换系数，取2.5；Qregmax为热泵的热出力上限。

其他关于热网的约束条件如式 （1）～（12）所示。

3 算例分析

3.1 算例系统

本文算例由IEEE33节点电力系统和6节点热力系统构成，其结构如图4所示。在热力系统侧包括Nd1处的热交换首站，Nd4，Nd5和Nd6处的换热站。热负荷分别设在Nd4，Nd5和Nd6处。6节点热力系统的其他参数见表1。

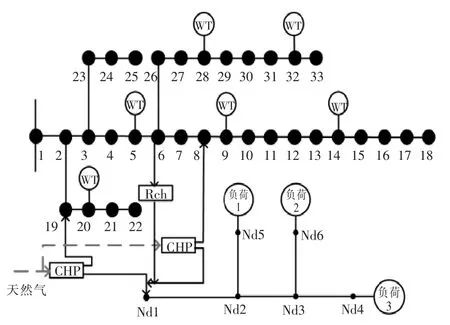
图4 IEEE33节点综合能源系统结构图Fig.4 Structure diagram of integrated system

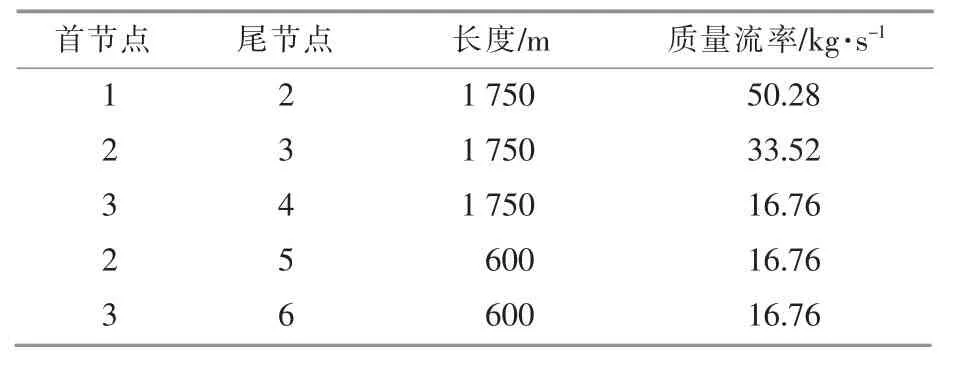
表1 6节点热力系统参数Table 1 Parameters of six-node heating system

管道损失系数设为2 W/（m·℃）。电、热负荷及室外温度曲线如图5所示。此外，天然气价格设为3.45元/m3；设τ=3。回水温度的上、下限分别设定为40℃和70℃，供水温度上、下限分别设定为55℃和100℃。

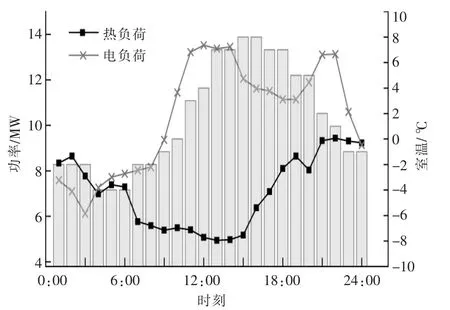
图5 电、热负荷及室温曲线图Fig.5 The curves of electricity，heating loads and outside temperature

电力系统的分时电价如图6所示。

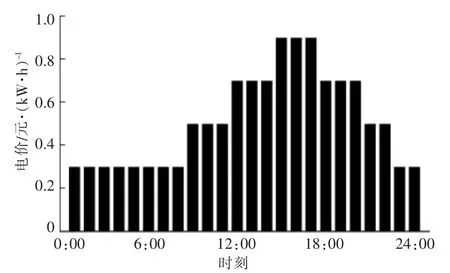
图6 分时电价Fig.6 Time-of-use electricity price

3.2 风电随机场景生成结果

在图 4 所示的配电网上，6 个节点（5，9，14，20，28和32节点）均接入了分布式风电机组。为简化分析，假定6个配电网节点所接入的风电机组的预测出力值相同。设定风电随机出力满足正态分布，以风电预测值为均值，以0.25倍均值为方差产生100 000个风电出力场景，然后采用Kmeans聚类算法将其削减为6个典型场景，由此获得每个典型场景的概率分布{ps}。以配电网节点5上的风电机组为例进行聚类分析，获得了6个典型场景出力曲线，给出了6类典型风电场景的出力值及各场景下的最大、最小边界值（图7）。

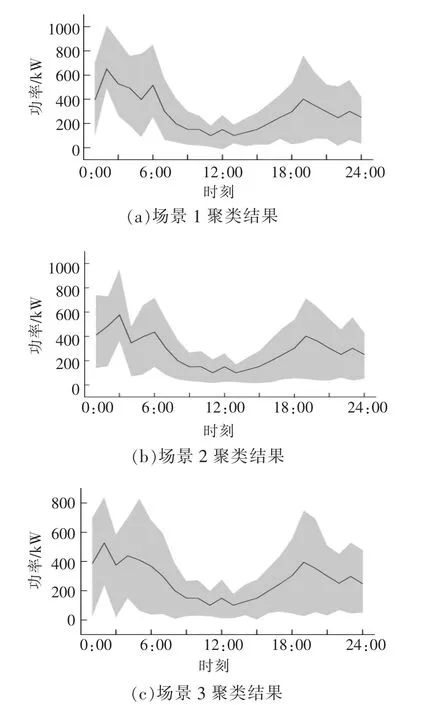
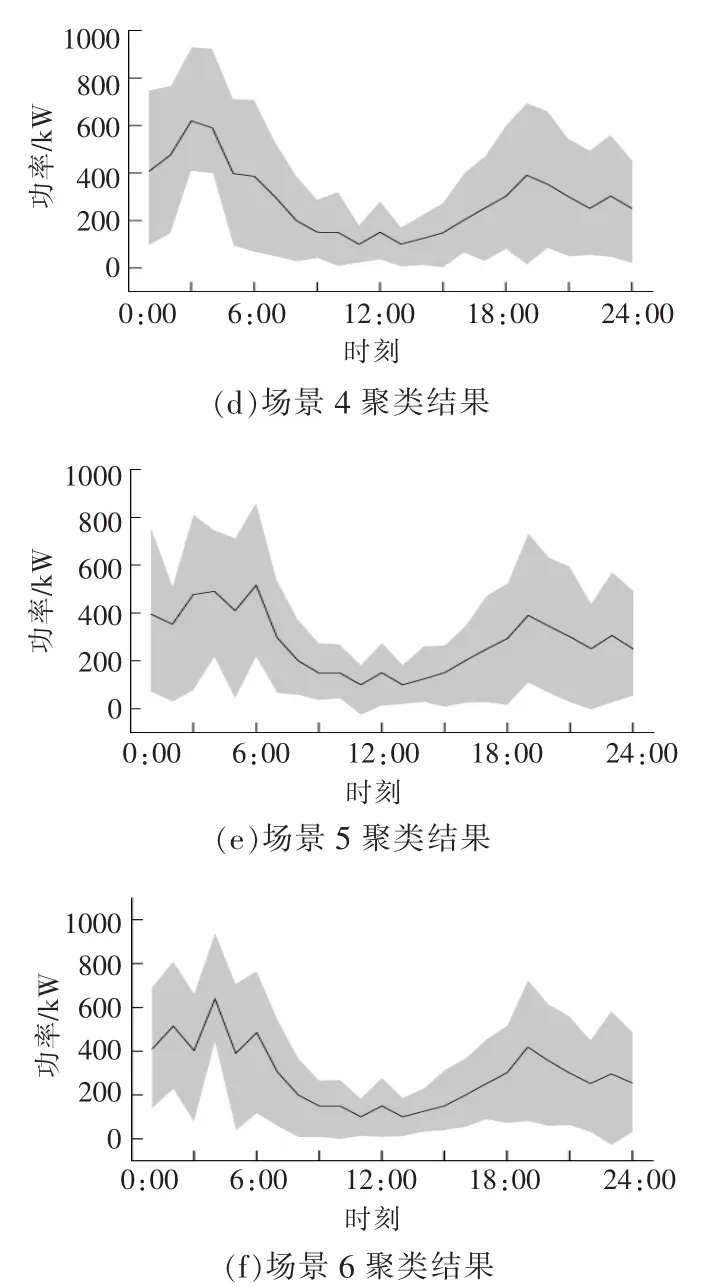
图7 6类典型场景下聚类结果Fig.7 The clustering results of six typical wind scenarios

由图7可以看出，风电典型场景主要在1：00-7：00 和 18：00-20：00 的出力值有明显差异，其余时刻的风电出力情况基本相似。

由聚类方法获得6个典型场景的概率分布{ps}列于表 2。

表2 6类典型场景的概率值Tab.2 The probability results of the six typical scenarios

3.3 随机优化调度结果

为分析考虑供热系统热储能特性对电-热综合能源系统调度结果的影响，设置了以下两种场景进行分析。场景1：不考虑热储能特性下的电-热综合能源系统随机优化调度；场景2：考虑供热系统热储能特性下的电-热综合能源系统随机优化调度。

上述两种场景均在6类典型风电场景下，按照表2中的概率分布值，以式（13）为目标函数进行优化计算。

表3给出了两种场景下的天然气购买成本和主网购电成本的计算结果。考虑了供热系统热储能特性下的综合能源系统的总运行成本更低，减少了4.86%。场景2中向主网的购电成本为23 628元，与场景1相比减少费用22.04%。场景2中的热泵装置购电成本与场景1相比有所上升。

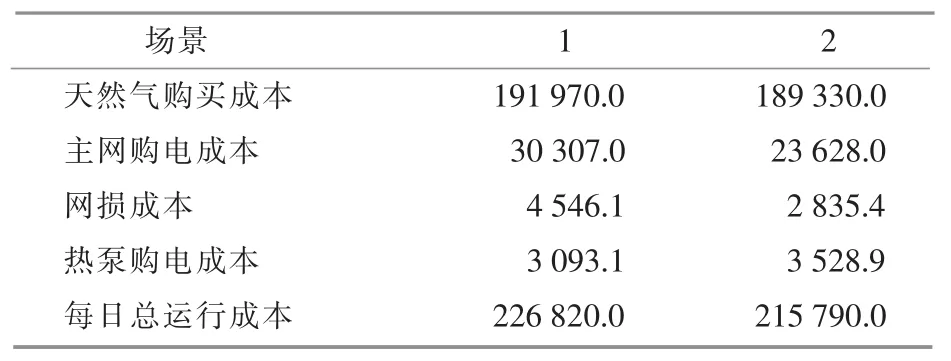
表3 两种场景下的购能成本Table 3 Costs under two scenarios 元

图8所示为两种算例场景下的系统热出力计算结果。场景1的系统热出力主要表现为跟随热负荷需求，可调性很差，出力波动十分局限；场景2的系统热出力和热需求明显不同步，主要在 1：00-8：00 和 11：00 以后。

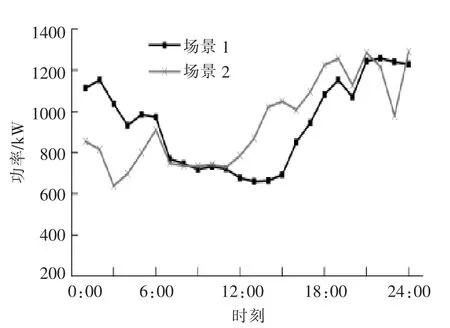
图8 两种算例场景下系统热出力结果Fig.8 The results of heat output under two scenarios

为分析内部各装置的作用，图9和图10给出了两个算例场景下的热出力。

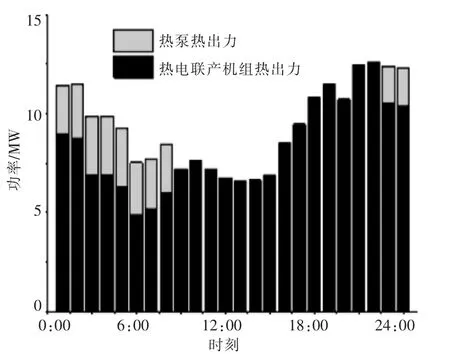
图9 场景1下各装置热出力柱状图Fig.9 The heat output under scenario 1

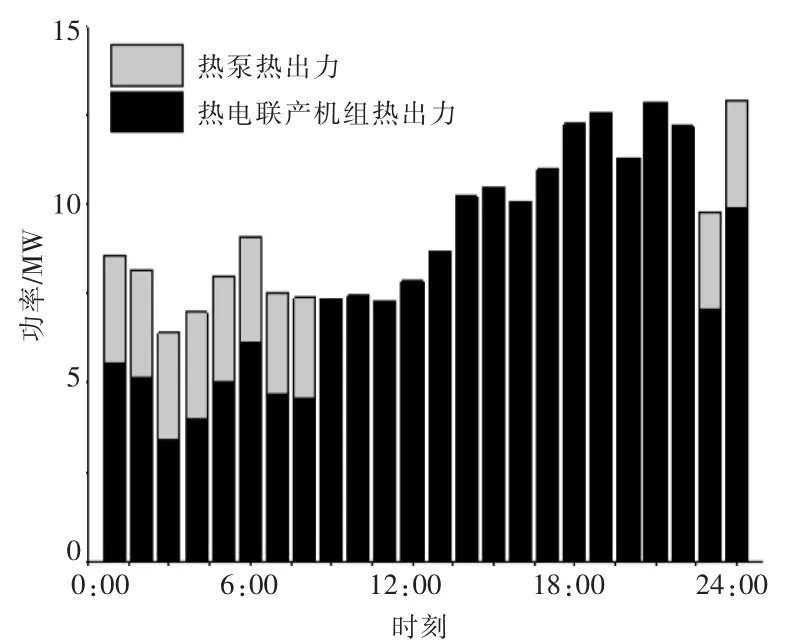
图10 场景2下各装置热出力柱状图Fig.10 The heat output under scenario 2

由图9，10可知，热泵装置在两个算例场景 下的热出力都主要在 1：00-8：00和 23：00-24：00。这是因为该时段的实时电价低于天然气价格，在满足电网潮流约束条件的前提下，通过热泵装置供热的经济性更好；在实时电价高于天然气价格时，通过热电联产机组供热的成本更低。

另外，在场景 2 的 1：00-8：00，综合系统中热泵装置和热电联产机组的热出力之和低于热负荷需求，此时供热网络发挥了“热储能”的作用，将管道中因为热延时存储的热量释放，热电联产机组也因此时段天然气价格较高而降低出力。在11：00-21：00，综合能源系统的热出力大于热需求，说明除了供应热需求之外，还有大量的热出力被存储在了供热管道中，相当于“热储能”的充能过程。由于该时段天然气价格低于实时电价，因此热电联产机组被充分利用于发电和供热。因此，供热系统热储能特性主要利用热网的延时性，通过对系统内能源设备的调度，将一部分热出力从电价较低的时段平移到电价较高的时段，从而打破实时供需平衡，提高综合能源系统的运行经济性。

图11显示了当回水温度下限固定为40℃，改变回水温度的上限时，综合能源系统的总运行成本。由图11可知，随着回水温度上限的逐渐提高，综合能源系统的总运行成本逐渐降低。这是因为供热系统的热存储能力逐渐增大，而成本降低的效果逐渐缓慢。回水温度的提升将对应着供水温度的提升，过高的供水温度将不利于供热系统的安全运行。

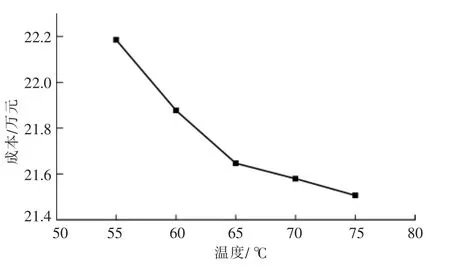
图11 不同回水温度下总成本值Fig.11 Cost under different return temperature

4 结论

本文以热电联产机组和热泵装置为耦合元件，充分考虑分布式风电出力不确定性问题，提出了考虑供热系统热储能特性下的电-热综合能源系统优化调度模型。通过算例分析得出如下结论。

①供热系统的供水管道具有热储能特性，在进行电-热综合能源系统的协同调度分析时，不可忽略其对调度过程产生的影响。

②热网管道具有一定的热延时性，即具有储能元件的特性。在实时电价环境中，通过对电价的响应机制以及综合系统内部各装置间的出力协调，可起到一定的削峰填谷作用，从而降低综合能源系统总运行成本。

③供热系统的储热能力与供、回水管道温度限制相关，即温差越大，储热能力越大。但出于对供热系统安全性考虑，供水温度不宜选择过高。