抗撞结构桩基关系研究的不足与措施
雷正保,刘 博
(长沙理工大学 汽车与机械工程学院,湖南 长沙 410114)
0 引言
随着交通基础设施建设的发展与完善,各种安装方便、设计美观且性能良好的公路防护安全设施(以下简称“抗撞结构”)被广泛应用于各国不同等级的公路。有限元仿真是抗撞结构设计、使用和安装的主要研究方法[1-3]。然而,许多抗撞结构尽管在仿真设计和实车碰撞试验中安全性能表现良好,却在实际应用过程中出现了结构失稳现象[2-4]。车辆冲破路侧护栏,驶出公路的交通事故时有报道[2],如图1所示。显然,抗撞结构未能对失控车辆进行有效防护,主要是因为其桩基关系未能满足预期的设计效果[8-9]。
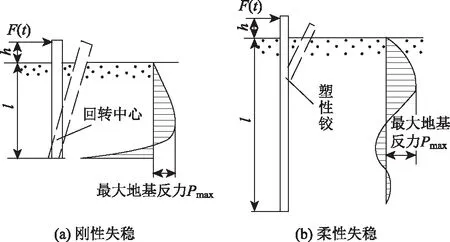
图2 桩基体系的破坏形态
对抗撞结构失稳现象进行分析,发现其桩基关系有两种类型:当土体强度较弱时,失控车辆冲击作用抗撞结构的瞬间,立柱不发生弯折,此时主要依靠土体变形吸收能量(图2 (a));当土体强度足够大时,失控车辆与抗撞结构瞬间的冲击载荷会引起系统结构及立柱发生弯折变形,并以此吸收车辆的动能(图2 (b))。不合理的桩基关系,将导致失控车辆突破抗撞结构的防护,驶入对向车道或路侧,引发二次事故[3]。但无论哪种桩基关系,抗撞结构系统的容许载荷都与土体性能参数有关。
因此,研究道路抗撞结构桩基关系中土材料模型,测量土的动力学参数,并根据公路交通安全法规要求,准确地设计桩基关系,是保证抗撞结构在交通事故中发挥作用的关键。该项研究对公路本质安全的提升,具有极大的工程意义。
1 研究现状
1.1 桩基关系试验研究
目前,桩基关系试验的研究主要集中在桩身结构对抗撞结构性能的影响,比如桩的材料、参数、埋深等。此外,还有水平静载条件下的桩基约束条件检测。而动态冲击条件下,桩基关系中的土结构参数(比如压实度、含水量等)对抗撞结构稳定性,容许载荷等动态力学特性的研究较少。
为全面了解桩基关系对抗撞结构性能的影响,学者基于全尺寸法和子结构法实施了大量的实车碰撞试验[4-5]。研究成果主要可归为3大类:(1)基于导波技术和弹性波法对立柱埋深检测的研究[6-7]。(2) 基于水平静载或准静载试验方法对桩基承载力的研究。与此同时,以有限元方法模拟静力加载试验,对桩基承载力及变形情况进行分析[7-8]。(3)基于摆锤试验和台车试验等动态冲击试验方法对桩基承载力的碰撞试验分析[8-9]。3类研究均集中于不同的立柱材料、立柱型号与埋深的桩基力学特性结果比较,很少有试验专门研究土体材料、类型、压实度以及含水量对桩基关系的影响。通过准静态和动态荷载的桩基关系试验和计算机模拟研究表明,汽车-抗撞结构碰撞的能量耗散和失控车辆重新定向能力均受制于土结构参数[10-12],而冲击载荷大小对土材料的力学特性参数的影响更为显著。

图3 抗撞结构桩基关系试验
1.2 土材料模型研究
研究人员以不同的弹性和塑性理论模型假设,开发了适用不同领域的土材料模型(以LS-DYNA为例)见表1。公路抗撞结构桩基材料模型的研究主要侧重于材料模型的遴选与定性验证,模型的参数来源于土工试验得到的参数。主要以两类试验为基础:(1)水平静载或准静载试验,见图3(b);(2)水平动载试验,见图3(c)。

表1 LS-DYNA土材料模型
基于静载或准静载试验的研究中,学者先以桩基静力学试验结果的先验知识为基础,分析比较多种材料模型的优劣,进而选出合适的材料模型。然后对比试验与仿真的桩基承载能力时间历史曲线结果,从定性角度验证所选土材料模型的准确性,如MAT005[11],MAT024[12],MAT173[21]和MAT193[13]等。美国陆军工兵队工程手册给出了不同类型土壤的杨氏模量、弹性剪切模量和泊松比的平均值,作为仿真模型的输入参数[14],见表2。

表2 土材料模型参数
基于动态冲击试验的研究中,学者利用摆锤试验法和台车试验法分别对桩基关系进行了实车碰撞试验,并利用有限元法对基于不同土材料模型(见表1)的桩基承载能力进行了定性验证分析, 模型参数来源于土工试验参数[15-17]。这类研究先基于实车碰撞试验,以桩基的动力学特性为基础,综合考虑模型的本构关系、土体损伤演化、数值稳定性、剪胀性和屈服强度特性等因素,进而挑选出合适的材料模型进行试验验证分析。验证过程主要也是定性对比试验与仿真的时间历史曲线响应,然后结合桩基形变产生的位移等指标定量评价材料模型的可靠性。
1.3 土材料模型参数研究
土材料模型参数的研究主要以土工试验(室内试验和原位试验)为基础,并结合有限元仿真对模型参数进行反演校准。根据目标函数的不同,主要有两类反演识别方法:(1)基于时间历史数据曲线的模型参数反演方法,如图4(a)所示;(2)基于本构关系曲线的土体参数反演方法,例如应力-应变曲线等,如图4(b)所示。
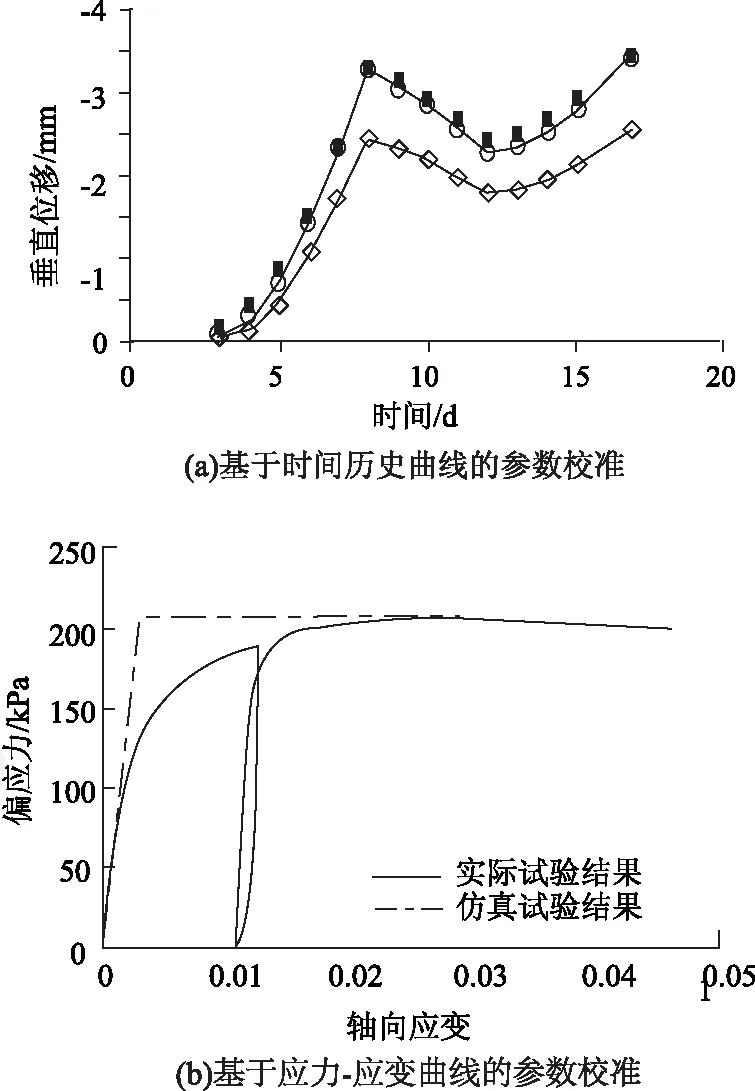
图4 基于土工试验的材料模型参数校准
在第1类反演识别方法研究中,学者主要通过应力-应变曲线等先验知识选定土材料模型,然后采用有限元法对室内试验或原位试验测试(如单轴拉伸、单轴压缩等)进行仿真模拟,再以两条时间历史曲线之间的距离或面积作为目标函数,结合一元响应或多元响应等逆向校准方法反演出样本土(或局部土样)的材料参数[16]。常用的时序曲线有材料应力、应变时序曲线,局部或峰值时间段内材料节点的位移时序曲线等。为保证模型的准确性,许多不同的模型参数校准方法被提出,如拟牛顿法[17]、人工神经网络方法等[18]。
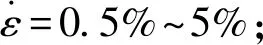
2 研究不足
2.1 桩基试验研究不足
抗撞结构设计及实车碰撞试验均在较理想桩基关系下进行[3-6]。两者都无法体现和立柱安装现场一致的桩基关系,使得抗撞结构在不同实地安装后,出现因桩基关系不达标而导致安全性能不确定的难题,甚至更糟的情况[3-7]。如图1所示:抗撞结构的失稳主要是由实际安装场地桩基关系较弱导致。此外,桩基关系与土体材料参数和冲击载荷强弱等因素显著相关。车辆撞击护栏立柱的过程是一个瞬时动态过程,在静态和动态载荷的作用下,护栏立柱与桩基土之间的力学特性是不一样的,现有的水平静载试验方法不能用于检测立柱的桩基约束条件。因此,在公路抗撞结构推广使用前对立柱桩基约束条件进行现场检测或者室内模拟是尤为必要的。
2.2 材料模型研究不足
基于公式(1)开发的土材料模型,模型的应变增量dεij为弹性应变增量与塑性应变增量之和,但很少考虑动态载荷下,土的应变率影响。此外,材料模型的定性验证结果也不可靠。
(1)
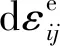
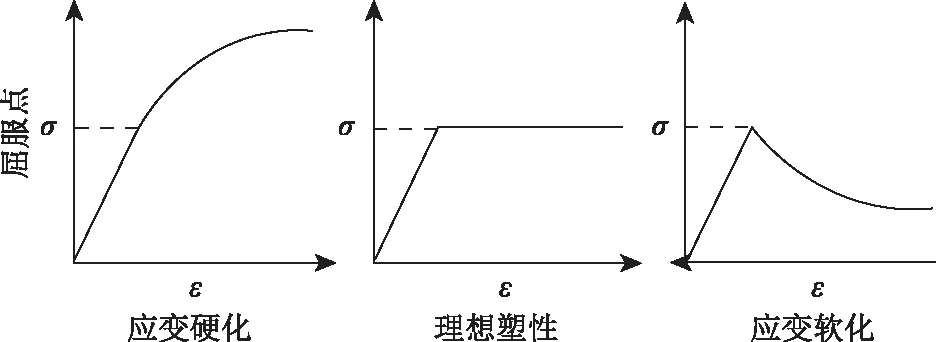
图5 弹塑性行为
如表1所示,FHWA土模型是研究道路安全抗撞结构相互作用而开发的专用模型,也是当前最复杂的土本构模型。该模型考虑了土体损伤演化、应变软化、孔隙水压力效应、应变速率效应和含水量效应等土体特性,但在开发应用时忽略了应变率的影响,而且待测参数过多,开发时只使用一个试验进行定性比较,试验结果不具有代表性,在很多研究中也均未被准确验证。此外其他大部分土材料模型适用于单桩或群桩的水平周期振动荷载,与冲击荷载有关的抗撞结构桩基研究较少,冲击荷载作用下横向抗力的组成分析也很少。随着现有研究的深入,无论是公路车辆碰撞还是水中的船桥碰撞,对结构的极端冲击载荷都在逐步增加,土体模型的研究迫切需要根据工程实际,分析冲击载荷下,土体的动力学行为特性。此外,有几个材料模型考虑了土体的时变性质、应变率效应[24],但由于求计算时间长,效率较低,也没有用于路基安全研究的应用实例。
2.3 反演识别方法研究不足
基于土工试验的反演研究主要侧重模型参数的校准。主要有如下局限性:
土工试验只能得到局部或采样土的土体参数,忽略了抗撞结构桩基的三维压力作用,得到的参数并不适用于大规模实车碰撞试验有限元模拟研究。基于土体应力-应变等本构关系曲线的模型参数反演识别方法,忽略了土体动力学特性的时间效应、即应变率效应,反演得到的参数可能高于或低于实际的土体参数。基于时间历史曲线的参数反演测试方法,以两条曲线之间的距离值作为目标函数的反演方法,缺点在于忽略了动态系统响应数据的时变性和动态相关性,没有综合考虑两条曲线的幅度、相位、形状误差,无法对计算结果的合理性进行解释,其反演结果不一定准确。当两条曲线长度不一致时,也无法对模型结果进行评价,具有局限性。
公路抗撞结构桩基材料模型参数的研究,往往先基于局部土样(或样本土)土工试验的材料参数反演识别方法得到土体测试参数,进而结合大规模实车碰撞试验对桩基材料模型进行定性的验证研究。不同于土工试验的单一载荷,碰撞试验冲击载荷影响面广,土体需考虑挤压、剪切、膨胀和软化等三维压力作用,还要考虑桩基周围全局土的大变形、大应变、大转动。因此,目前抗撞结构桩基关系材料模型及参数反演研究需要考虑抗撞结构的实际物理试验与有限元仿真之间时间数据曲线的动态特性定量量化方法,同时还考虑材料模型和模型参数的耦合性,对两者进行综合反演分析,以便得到最合适的材料模型及参数。
3 研究措施
得益于LS-DYNA等计算机软件的开发应用,桩基关系问题得到有效研究和分析。但桩基关系中土材料模型的试验、选择与模型校准仍然是桩基关系设计及使用的难点。有必要从以下几个方面进行改进。
3.1 桩基约束条件试验系统研究
大力开展抗撞结构桩基约束条件检测的研究,并立足于我国公路安全设施设计法规,完善桩基系统的实车碰撞试验及有限元建模,设计合理地桩基关系。
在抗撞结构等防护安全设施安装使用前,需要对桩基约束条件进行现场检测。但由于在静态和动态载荷的作用下,桩基土的动力学性能与参数不一致,因此水平静载试验方法并不能应用于立柱桩基约束条件的检测。另一方面,可利用相关硬件设备:包括私人定制台车、加速度计、压力带状开关、高速和标准数字摄像机以及静态摄像机,对不同道路安装环境(中央分隔带和路侧)和碰撞条件下的桩基关系组织室内台车碰撞试验,如图6所示。
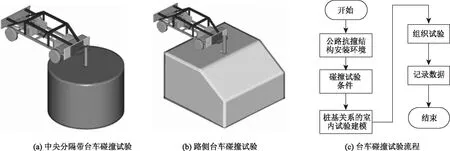
图6 桩基约束条件试验系统
首先,基于《公路交通安全设施设计细则》和《公路护栏安全性能评价标准》等法规,对公路护栏等防撞设施安装环境和设置要求进行分析。然后总结不同防撞等级的护栏碰撞试验规定,开展实际交通车辆与中央分隔带(图6(a))和路侧(图6 (b))等抗撞结构桩基关系的试验。再调整试验台车的质量、速度、冲击高度,以公式(2)[25]对台车试验和实际交通车辆试验中的桩基关系进行匹配,完成室内模拟试验规划。
(2)
式中,FC为实际车辆平均碰撞力;Ft为台车平均碰撞力;MA为桩基试验中立柱力矩臂;Emb为桩基试验中立柱埋深。
通过试验得到的桩基承载能力的时间历史曲线,以定量对比结果作为评价指标,进而利用子结构法建立室内试验模型,最后组织碰撞试验以获取不同冲击载荷条件下,土体损伤演化过程中的动力学数据。与碰撞试验数据相结合的反演识别法将基于实际试验,对土材料模型参数进行反演识别,从而对桩基约束条件进行检测。
3.2 土材料模型研究
土作为公路的重要载体,其动力学特性十分复杂。不同载荷下的同一种土体,也会表现出不同的应力路径依赖性,即应变率效应。故应从实车碰撞试验出发,结合文献研究和理论分析,开发或选择合理的土材料模型来模拟桩基关系。
根据试验报告总结,土体动力学特性不仅随含水量、压实度和粒径的变化而变化,也与立柱受冲击的车辆载荷有关[26-27]。冲击载荷越大,桩基作用反力的初始峰值力,以及初始峰值力之后的作用反力均呈现增大的趋势,而在同一载荷的持续剪切作用下,作用反力会逐渐减小,如图7所示。土体含水量和黏性也会增大其应变率效应,含水量越多或者黏性越大,应变率效应越明显。目前的土材料模型均基于弹性理论和塑性分析假设,假定应力-应变路径与应变率无关,或者影响很小可以忽略不计,在剪切失效后期也很少考虑模型的剪切应力软化,这与实际道路土材料力学特性研究情况不完全相符。从工程实际出发,抗撞结构桩基材料模型必须考虑土的应变率效应和连续剪切产生的应变软化效应。
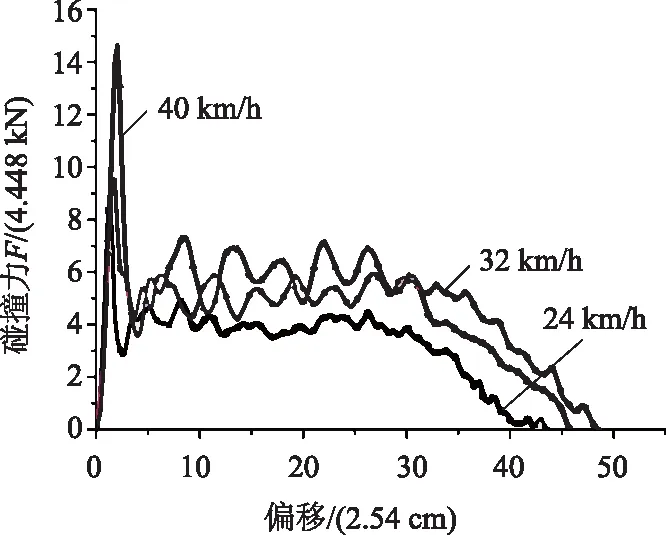
图7 台车碰撞力与位移曲线
结合实车碰撞试验和土材料模型理论分析研究,立柱受动力载荷时,土体的动极限抗力总是大于其静极限抗力,载荷越大,抗力变化越明显。因此,理想地基材料模型的应力-应变曲线应大致符合图8所示趋势。其他条件不变,峰值剪切应力和残余剪切应力均随台车冲击速度的增大而增加。同一冲击速度的台车-桩基碰撞试验,残余剪切应力随位移或剪切应变的增加先到达峰值剪切应力,然后保持一段时间不变,后期则随之减小。
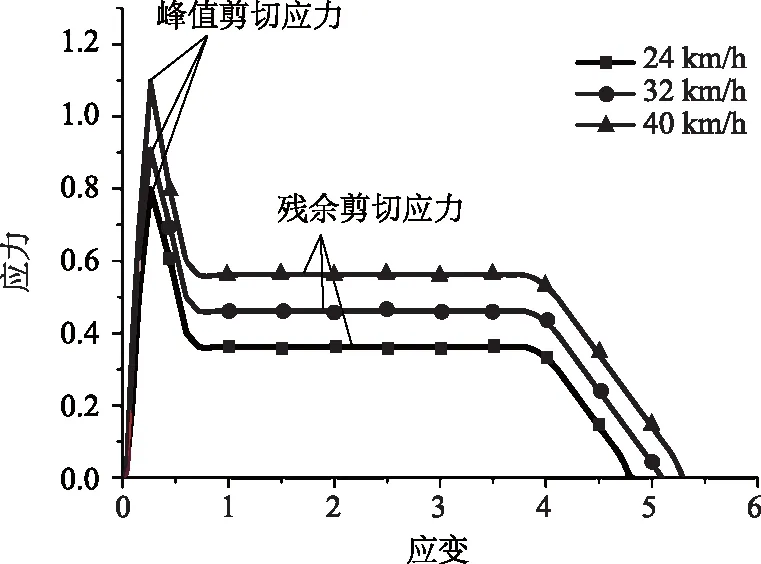
图8 理想的地基应力应变曲线
基于混凝土加载试验的有限元验证分析,有几种材料模型充分考虑了材料的应变率效应、侧限(或围压)效应和剪切软化特性[28-29],如MAT016,MAT072R3,MAT084,MAT159,MAT272,初步符合道路桩基关系研究的需要。所有模型均采用三不变量的各向同性非线性弹塑性假设,屈服(破坏)函数的一般形式为:
Y(I1,J2,J3)=0,
(3)
式中,I1是应力张量的第一不变量,描述了体积响应关系;J2、J3是剪应力张量的第二和第三不变量,描述了剪切响应关系。
3.3 土材料模型参数反演识别方法研究
亟需一种基于桩基实际碰撞试验的材料模型参数反演识别方法,对材料模型及参数同时进行反演识别,以便充分考虑各部分变量的耦合影响。
针对抗撞结构桩基材料模型及参数的反演研究方法的不足,存在两点需要改进:(1)材料模型与模型参数相互耦合,且对试验结果均有极大的影响。基于局部土样(或样本土)得到的测试参数无法直接用于碰撞试验,桩基大变形时的材料模型参数输入。(2)作为评价指标的目标响应为时间历史数据,具有极强的时间相关性和时变性。简单计算两条曲线距离的评价方法不具有说服力,曲线的幅度、相位和形状等特征均应该纳入评价指标。
以动态时间弯曲距离等能度量不等长时序曲线综合误差的算法作为目标函数、结合智能优化算法和双层优化思路的反演识别方法,将从定量的角度优选出最合适模型及其参数,如图9所示。
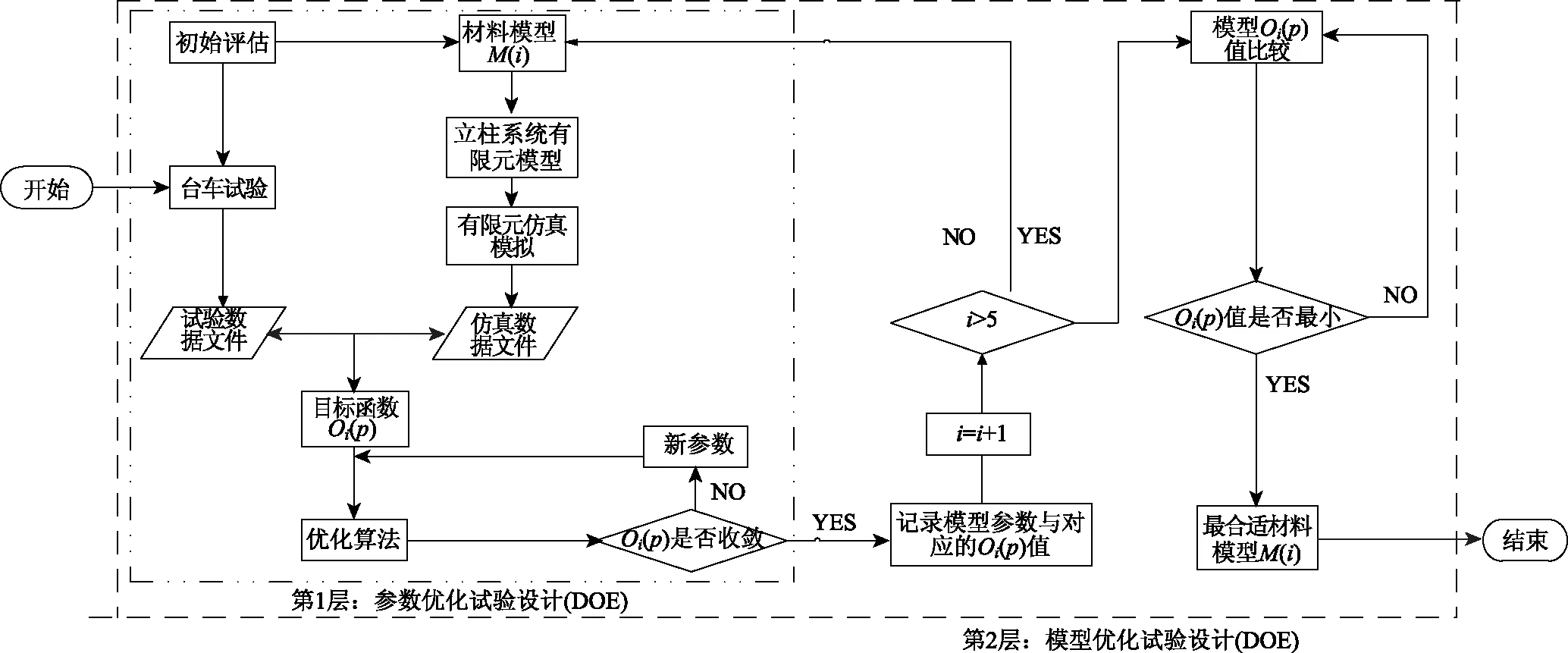
图9 反演识别法流程图
如图9所示:第1层参数优化试验设计(DOE)以碰撞试验为基础,结合仿真分析搜寻不同材料模型的最合适参数。首先,以子结构法建立台车-桩基碰撞试验模型并进行试验测试。其次以台车碰撞试验数据为基础,利用动态时间弯曲距离算法构建目标函数Oi(p)。然后结合优化算法对试验进行最优化求解,当目标函数Oi(p)值收敛时,即得到了该模型的最合适参数,并记录当前模型M(i)的材料参数。第2层优化嵌套第1层参数优化设计,目标是优选出最合适的材料模型。首先通过第1部分的参数优化设计,得到各材料模型最合适的模型参数和目标函数值Oi(p)。然后对5个目标函数值Oi(p)进行分析比较,优选出其中的最小值,此时该值对应的材料模型及参数即为最合适的材料模型参数。
4 结论
有限元法能有效分析桩基相互作用的三维问题,为研究者提供全面的应力-应变行为、能量变化、实际的破坏情况和复杂的物理响应等详细的试验过程信息,有助于抗撞结构桩基关系研究的参数化分析。随着计算机技术的不断革新,其计算效率不断提高,研究者们致力于利用有限元法对抗撞结构桩基相互作用进行建模分析与研究。研究道路抗撞结构桩基关系中土体的材料模型,测量土材料模型的动力学参数,成为抗撞结构桩基关系设计研究亟待解决的问题,并对道路本质安全性建设具有重要指导意义。
——结构相互作用的影响分析

