知识与数据驱动机器学习模型的参数可辨识性理论分析与研究

张树兴 蒋红卫

摘  要：随着现代经济水平的不断提升，现代社会逐渐成信息传播的时代，在此背景之下，基于信息数据驱动的各种机器逐渐成为数据处理的关键技术。分析知识与数据驱动机器学习模型的参数的可辨识性，对于相关研究来说具有重要的价值。基于此，文章主要对知识以及数据驱动机器学习模型的参数可辨识性的理论参数进行了分析，对其研究进行了探究分析。

关键词：知识与数据驱动机器学习模型;参数可辨识性;分析以及研究

中图分类号：TP181         文献标志码：A         文章编号：2095-2945（2020）09-0014-02

Abstract： With the continuous improvement of modern economic level， modern society has gradually become an era of information dissemination. In this context， various information data-drivenmachines have gradually become the key technology of data processing. It is of great value for related research to analyze the course identification of the parameters of knowledge and data-driven machine learning model. Based on this， the paper mainly analyzes the theoretical parameters of the identifiability of knowledge and data-driven machine learning model.

Keywords： knowledge and data-driven machine learning model; parameter identifiability; analysis and research

基于辨識研究发展角度分析，辨识是数学模型以及控制系统中的关键以及集成的内容。辨识概念研究的主题在不断的拓展。在系统辨识理论中是较为关键的内容。可辨识性是机器学习的核心内容。现阶段并没有得到深入的研究。基于知识以及数据驱动机器学习模型角度进行分析，分析参数可辨识性，对其进行分析，了解其今后的发展轨迹以及主要特征具有重要的价值意义。

1 知识与数据驱动机器学习模型的参数可辨识性理论分析

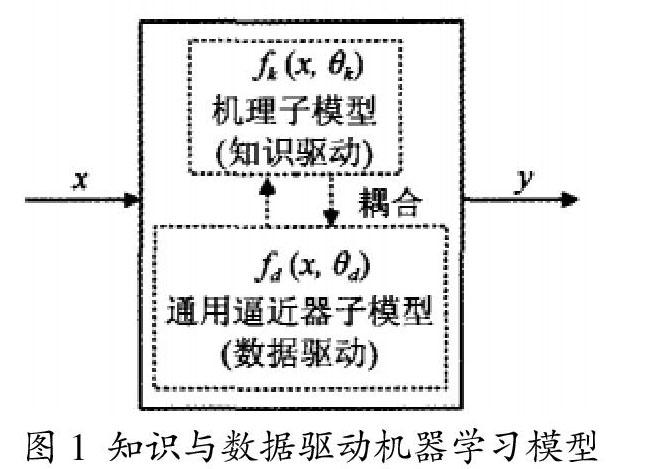
模型对象为“基于知识与数据共同驱动的模型”，此模型的结构原理如图1。

其表示的就是两个子模型之间互相作用的运算以及数据驱动的子模型，可以通过机器X射线决策树以及神经元网络、也可支持向量机。参数辨识性的分析中，知识以及数据的驱动机器学习模型有重要的价值。知识驱动子模型参数变量进行处理，这也是获得参数正确估计的关键。

为了统一模型框架，将传统知识驱动或者书籍驱动模型作为例子进行分析，模糊系统以及概率图等模型相关通过单一结构化的知识表达模型可以定义为新模型的一种，新模型利用具有非结构化的先验知识以及具有任意类型的动态模型进行处理。此模型与传统的模型具有一定差异，新模型的耦合模式以及DD子模型的特征可以为参数的可辨识性提高充分的空间。通过调整模型的方式则可以达到对模型可辨识度的实际状况的调整，其具有一定的物理意义。也为不可辨识参数的转变提供可行。

今后，机器学习的模型呈现智能化的特征。利用知识以及数据，要基于“归纳”与“演绎”进行处理，为新的模型提供参考。在大数据的支持之下会产生不断的完善。经典统计理论中，可辨识度属于基本的假设，多数的统计性质均是用过假设的方式进行研究。例如，极大似然估计以及Bayes的后验分布中的渐近正态性。

可辨识性研究以及机器学习领域具有密切的关系。其中隐因子模型、变分Bayesian矩阵分解之间有着密切的关系。在机器学习领域中学习机具有奇异性的特征，其对机器学习产生了较大的影响。在参数模型以及学习算法、学习动态、Bayes推断等领域中具有重要的影响。对此，要通过创新化的方式对奇异学习机进行统计分析。

2 知识与数据驱动机器学习模型的参数可辨识性研究

2.1 奇异统计模型参数空间的几何结构

基于Amari信息几何特征，利用模型的一阶近似，非奇异统计模型参数之间的空间局部结构要对统计流形的切空间进行表示。而高阶近似则可以基于信息集合的放射链接以及相关的e-曲线和m-曲线获得。

而在奇异模型的统计流形中，并没有在奇异点中并没有切空间。通过切锥进行分析。通过同意的方式对奇异统计的具备结构进行研究分析，可以将其观测的等价参数通锥 （Cone）的方式进行嵌入，在正则流形中进行分析。

机器学习领域中的研究较大，通过对层次神经网络进行研究，发现在模型参数中的等价类并不是呈现孤立性的集合性，而是呈现连续统的方式进行存储，充分的展示了奇异模型参数的几何结构特征。

2.2 模型选择

模型选择是机器学习的重要内容。进行模型选择中主要根据可辨识性以及灵活性、吝啬性等方面进行分析，较长应用的模型准则主要有Akaike information criterion（AIC）Bayesian information criterion（BIC），Minimum descriptionl

ength（MDL）等等。

神经网络建模处理中，应用AIC作为其标准，但是结果并不理想，而出现此种问题主要就是因为神经网络模型自身的奇异性造成的。

网络信息准则（NIC）分析了奇异性的特征，其理论以及数值的实验较为良好。而NIC的基本思想与Vapnik结构风险中的极小化归纳原则中要构建具有嵌套性的函数集合特征，但是其操作较为困难。基于其统计角度进行分析，AIC的极小化模型具有泛化误差。在奇异模型中的泛化误差中的正则模型具有复杂的性质特征。在奇异模型中其BIC缺陷、MDL缺陷类似于AIC。而Bayes模型对比分析，模型奇异性是必须要综合的因素。奇异模型中要应用标准的选择标准，这也是机器学习的重要内容。

2.3 学习算法

学习模型中的相关参数维数以及非线性的程度会呈现快速增加，在学习中会产生大量的计算资源，为了提升学习参数过程的速度，就要加强对奇异性的学习算法的研究。多层感知其网络的研究中为了加快对后向传播算法的研究提升收敛速度，学者对其进行了大量的研究，其中自适应步长动量的方法虽然有效，但是在本质上来说都是梯度下降的一阶算法，无法在根本上达到解决平台现象的目的。而牛顿法、共轭法等方法虽然分析了参数空间的曲率信息，但是其开销较大，仅仅具有收敛的特性，都属算法仅仅适合批量的方式，无法适合大规模的数据以及在线学习的要求。

在平台中出现慢流形的主要问题就是模型自身的奇异性，为了有效的克服出现的慢收敛的问题，通过自然梯度下降算法分析，可以综合算法中参数空间中的流形结构，达到提升收敛速度的目的。分析自然梯度下降算法的复杂性问题，综合统计物理机理对其进行分析。整体上来说，自然梯度下降算法中的复杂度较高，对此，在奇异模型中仍需要更高的算法。

2.4 学习过程的动态轨迹分析

在进行奇异性的研究中，学习过程中的动态轨迹的分析尤为关键。奇异模型中的参数具有不可辨识的特征，因此其相关的观测等价参数的误差函数是相同的，误差曲面中多数的地方为平坦的状态。受到其影响导致学习过程相对较为缓慢，会产生严重的后果：

学习过程缓慢，低纬流形上的学习轨迹停留时间则就会过长，随着其训练数据的随机噪声的作用才会导致其出现下降的趋势。导致其陷入到局部的极小值中。误差曲面中的参数学习轨迹岭线完全平坦。在理论的角度进行分析可以确定，在奇异模型中，Batch学习方式则就会对在训练中产生的随机噪声产生作用，平滑随机噪声;这样则就会使得学习过程出现低维流形以及局部的极小点。通过Onlie的学习方式则就会使得学习平坦区域中的动态轨迹逃离。由此可以证明，奇异模型中Online方法更为合适。在学习中为了充分的分析参数的学习轨迹，通过对多层感知网络以及高斯混合模型中的参数学习的动态轨迹进行分析，了解参数空间中的学习动态的向量场。但是进行奇异模型的学习过程的动态轨迹分析，其并没有普遍适应的结果。

2.5 泛化误差

泛化误差是基于Cram6r-Rao范例开展的。奇异统计模型的泛化误差计算则要综合模型中的特殊性质进行分析。高斯混合模型中的数似然比具有奇异性的特征。出现此种特征主要就是因为奇异统计模型中的数似然比影响。神经网络中利用简单的线性模型则可以充分的分析多层感知器模型的渐近性质以及泛化误差结果更为精准。

现阶段，学界中主要就特殊模型进行研究，要加强对奇异模型的通用结果的深入研究。

2.6 Bayes推断

通过Bayes学习方式进行处理，利用先验知识的方式，可以缓解过拟合的问题，其具有显著的泛化性特征，在奇异学习中，会遇到理论性的困难。应用先验知识“无信息先验”进行处理，则光滑先验密度奇异点构成等价类则呈现无穷大的特征，导致模型后验分布会更加偏向奇异点，但是违背了“无信息先验”的基础原则，不符合常理，同时，在奇异模型中Bayes后验分布，利用Hironaka奇异性对定理分解以及Sato公式，在奇异机器学习中代入几何以及代数分析，研究分析不同层次的奇异学习的预测分布的性能，可以获得一定结果。其理论主要几个方面，得出了一系列结果：

第一，分析数似然比函數标准型以及随机复杂度中存在的收敛性问题。在Bayes分析中，分析两个方程与训练误差、泛化误差直接的对称性关系。第二，分析奇异性的不同影响，是机器学习的基础的知识，是今后研究的重点。

3 结束语

机器学习理论为实践研究提供了全新的视角以及参考。对其相关概念以及知识要点进行分析，对于自变量的设定以及公共政策的调整等的各项提供参考，也为典型的复杂巨系统问题的演变激励研究提供了参考。知识与数据共同驱动的思维以及其参数可辨识性的研究对于深度学习以及人工智能等理论具有重要的价值。

参考文献：

[1]沈国良，钱济人.基于系统辨识的机器学习模型参数可调性研究[J].自动化应用，2019（03）：97-98.

[2]胡包钢.统计机器学习中参数可辨识性研究及其关键问题[J].自动化学报，2017（10）：3-12.

[3]冉智勇.知识与数据驱动机器学习模型的参数可辨识性理论研究[D].中国科学院大学，2014.