均质土坝三维动力响应分析饶为胜
唐艳梅

摘 要:基于有限元软件ABAQUS,运用等效线性模型子程序,对某小型均质土坝进行三维动力响应分析。计算结果表明,地震作用下坝顶、上游坝坡近坝顶等位置有可能会有坝料松动、滑落的可能,防渗墙可能发生受拉破坏;竖直向地震永久变形最大值发生在坝顶靠近库外坝坡的一侧,且随着高程的增大,地震永久变形增大。通过分析土坝地震永久变形、动位移以及防渗墙的响应,验证了这种方法对于均质土坝的适用性,相关结论可为类似工程的地震设计提供参考。
关键词:均质土坝;等效线性方法;动力响应
中图分类号:U445.55 文献标志码:A 文章编号:2095-2945(2020)09-0006-05
Abstract: Based on ABAQUS and the subroutine of equivalent linear model, the three-dimensional dynamic response of a small homogeneous earth dam is taken. The results show that under the earthquake, there may be loosening and sliding of dam materials at the top and upstream dam slopes near the top of the dam, and tension failure of the cut-off wall may occur; the maximum vertical seismic permanent deformation occurs on the side of the dam top near the dam slope outside the reservoir and the seismic permanent deformation increases with the increase of the elevation. The applicability of this method to homogeneous earth dams is verified by analyzing the earthquake permanent deformation, dynamic displacement and the response of cut-off wall of earth dams, therefore, this conclusions can provide reference for seismic design of similar projects.
Keywords: homogeneous earth dam; equivalent linear method; dynamic response
1 概述
小型水庫一般为均质土坝,对于此类工程,《水电工程水工建筑物抗震设计规范》(NB 35047-2015)规定采用拟静力法进行地震设计,但该方法缺点较多[1]。这导致使用该方法设计的均质土坝存在很大的地震安全性隐患。随着上世纪中后期有限元法和计算机的迅速发展,采用有限元法进行土坝动力响应分析成为趋势。根据采用的材料本构的不同,土坝动力响应分析主要包括两种方法,即基于黏弹性模型的等效线性分析方法和基于完全弹塑性的非线性分析方法[2-4]。
等效线性方法采用土体黏弹性模型,可以很好地模拟土体在往复荷载下的滞回性,通过迭代近似反映土体的非线性。由于每个迭代过程是线性的,这种方法计算效率高,一般能够提供较合理的结果。在每个动力计算时段后加入半经验的残余变形计算公式,计算该时步的残余变形。等效线性方法概念简单,易于有限元编程实现,在模型参数的取值以及实际工程应用上积累了丰富的经验,是目前岩土工程地震分析的主流方法。谢庆明等将沈珠江提出的残余变形计算公式与等效线性模型相结合,基于ABAQUS平台提供的UMAT子程序接口开发了等效线性模型有限元程序,对轿子山水库进行了三维地震响应分析[5]。谢红强等基于等效线性模型,采用三维非线性动力有限元方法,对位于强震区的东风水库心墙土石坝工程进行了地震响应分析[6]。以上两位学者的研究中,均采用了沈珠江提出的残余变形计算公式对坝体永久残余变形进行分析。刘汉龙、费康等也基于等效线性模型对土石坝的地震响应进行了大量研究,并提出了一系列土石坝地震永久变形的分析方法[7-9]。
本文基于等效线性分析方法,结合沈珠江残余变形计算公式对某均质土坝进行动力响应分析,相关结论可为类似水库、路堤、地基的地震设计提供参考。
2 等效线性模型
等效线性模型用粘弹性Kelvin模型来反映土体在周期荷载下的滞回性。如图1所示给出了粘弹性模型的示意图,即一个线弹性弹簧和一个阻尼器并联,其应力应变关系为:
根据坝体的静应力状态和地震过程中的动力反应,结合实验结果,可以得到坝体在地震过程中累积的残余应变势。土石料的残余应变势采用沈珠江模型:
式中:?驻?着v和?驻γ分别是动力残余体积应变增量和残余剪切应变增量;N和?驻N分别为总振动次数及其时间增量;c1、c2、c3、c4和c5为5个试验参数。
由于相邻单元的互相牵制,由此确定的残余应变势并不是各单元的实际应变。在常规的有限元计算中,为使各单元能产生与此应变势相协调的实际应变,需在网格上施加等效静节点力。在ABAQUS中,可将得到的残余应变作为初始应变,计算出初始应力,再通过地应力分析步间接得出残余变形[10]。
3 计算模型
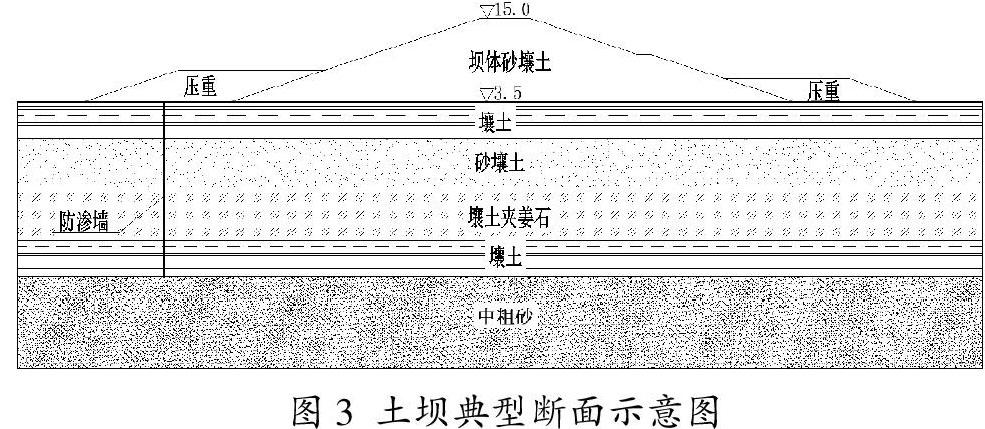
某小型水库为均质土坝,坝高11.5m,位于深厚覆盖层上,图3为该水库围坝典型断面示意图。虽然该坝体高度不大,但地基相对比较软弱,拟定模型计算范围为:(1)坝踵上游(库区内):至少大于2倍坝高,包括地基中防渗墙,各坝段均取200m,其中防渗墙中心距坝轴线37.5m。(2)坝趾下游(库区外):至少大于2倍坝高,取250m。(3)地基:大于1.5倍坝高,计算范围超过防渗墙最大深度,取50m。
3.1 三维计算网格
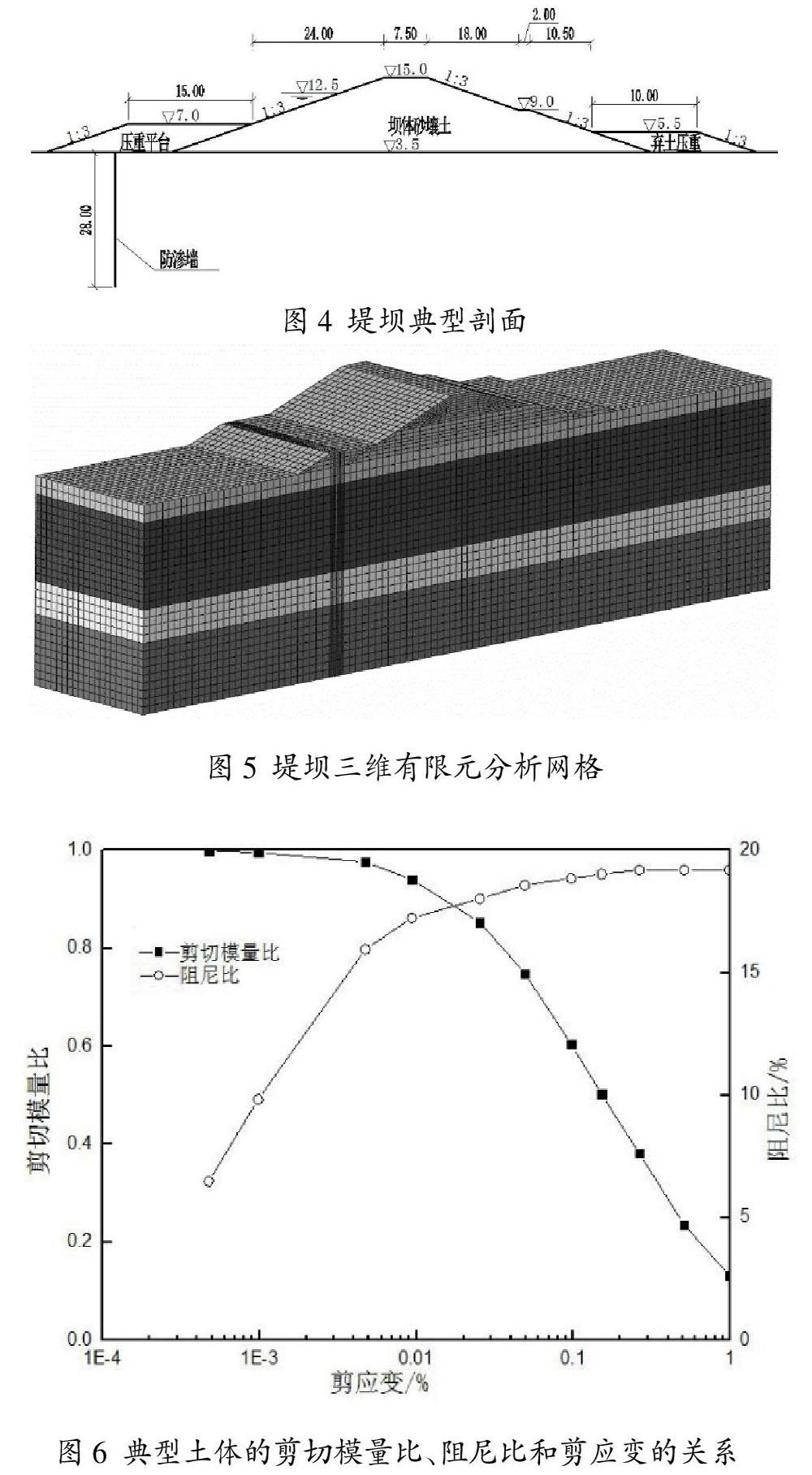
图4为双王城水库典型剖面,据此建立有限元模型,图5为三维有限元分析网格,坝体、坝基和防渗墙单元类型均为八结点实体单元,三维有限元分析模型共有71736个结点。
3.2 材料参数
防渗墙采用线弹性模型,弹性模量取10GPa;土体采用等效线性模型,材料参数取自设计报告,典型土体的剪切模量比、阻尼比和剪应变的关系如图6所示,工程动力特性参数按已有研究选取[11]。
3.3 地震动时程
动力计算采用沈珠江等效线性模型,考虑在三维场地地震下坝体的动力响应。按7度设防标准,将地震峰值加速度取为0.3g,按照规范,竖直向地震波乘以折减系数0.67,并考虑遇合系数0.5,图7为本次计算使用的地震波时程曲线。
4 计算结果分析
对于土坝的地震结构设计,主要关注坝体地震永久变形、动位移以及防渗墙动力响应。
4.1 防渗墙动力响应
图8给出了典型剖面的坝顶加速度时程曲线,图9为坝体加速度极值等值线,图10为防渗墙最大主应力时程曲线。由计算结果可看出,水平向加速度随高程增加而增大,加速度最大值发生在坝顶处。竖向加速度不仅由坝基向坝顶逐渐增加,而且在同一高程处,大体表现出了由坝内向坝坡方向逐渐增大的趋势。由于坝体形状大致对称,加速度响应也沿坝轴线大致对称分布。地震波下坝顶顺河向加速度最大放大倍数约为2.38,坝顶竖直向加速度最大放大倍数为1.4。在地震作用下,坝顶、上游坝坡近坝顶等位置有可能会有坝料松动、滑落的可能性,建议在上述区域采取适当的抗震加固措施。防渗墙的主应力变化趋势和地震加速度时程曲线较为一致,防渗墙最大主拉应力为0.59MPa,可能会受拉破坏。
4.2 动位移响应
图11给出了典型剖面坝顶水平向动位移时程曲线,图12给出了地震波下典型剖面动位移极值分布。由计算结果可看出,水平向动位移最大值发生在坝顶处,竖直向动位移最大值发生在库外坝坡靠近坝顶处。典型剖面地震波下水平向动位移最大值为2.6cm(向库外),地震波下竖直向动位移最大值为0.8cm(竖直向下)。水平向动位移的最大值明显大于竖直向动位移最大值,这与两个方向上的加速度放大系数所表现出来的差别是一致的。
4.3 地震永久变形
图13给出了地震波下典型剖面地震永久变形分布。由计算结果可以看出,地震顺河向永久变形以向库外为主,地震波下典型剖面向库外的顺河向地震永久变形最大值为:0.9cm。竖直向地震永久变形以竖直向下为主,随着高程的增大,地震永久变形增大,竖直向地震永久变形最大值发生在坝顶靠近库外坝坡的一侧,地震波下典型剖面竖直向下地震永久变形最大值为:2.4cm,占最大坝高的0.21%。可以看出,坝体在地震中的沉陷比水平位移大,体现了土石坝在固结应力和循环荷载作用下的残余体积变形特性。
5 结论
通过对某均质土坝进行三维动力响应分析,可以得出如下结论:(1)在地震作用下,坝顶、上游坝坡近坝顶等位置有可能会有坝料松动、滑落的可能性,建议在上述区域采取适当的抗震加固措施;防渗墙最大主拉应力为0.59MPa,可能会发生受拉破坏。(2)水平向动位移最大值发生在坝顶处,竖直向动位移最大值发生在库外坝坡靠近坝顶处,水平向动位移的最大值明显大于竖直向动位移最大值,这与两个方向上的加速度放大系数所表现出来的差别保持一致。(3)地震顺河向永久变形以向库外为主,竖直向地震永久变形以竖直向下为主,坝体在地震中的沉陷比水平位移大,体现了土坝在固结应力和循环荷载作用下的残余体积变形特性。
参考文献:
[1]国家能源局.水电工程水工建筑物抗震设计规范:NB35047-201
5[S].北京:2015.
[2]Liang F, Chen H, Huang M. Accuracy of three-dimensional seismic ground response analysis in time domain using nonlinear numerical simulations[J]. Earthquake Engineering and Engineering Vibration. 2017,16(3): 487-498.
[3]Elgamal A, Yang Z, Parra E. Modeling of cyclic mobility in saturated cohesionless soils[J]. International Journal Plasticity. 2003,19:883-905.
[4]Elgamal A, Yang Z, Parra E. Computational modeling of cyclic mobility and post-liquefaction site response[J]. Soil Dynamics and Earthquake Engineering. 2002,22:259-271.
[5]谢庆明,江守燕,曹庆明,等.沥青混凝土心墙风化料坝三维地震响应分析[J].三峡大学学报(自然科学版),2015,37(01):22-28.
[6]謝红强,肖明砾,何江达,等.强震区心墙土石坝地震反应三维非线性分析[J].水力发电学报,2009,28(05):108-113.
[7]刘汉龙,费康.考虑残余体应变的土石坝地震永久变形分析[J].岩土力学,2013,34(06):1687-1695.
[8]费康,朱凯,刘汉龙.深厚覆盖层上高土石坝抗震稳定性的三维分析[J].扬州大学学报(自然科学版),2008,11(01):74-78.
[9]岑威钧,顾淦臣,隋世军.深厚黄土覆盖层上土石坝地震响应特性分析[J].防灾减灾工程学报,2009,29(01):51-56.
[10]费康,刘汉龙.ABAQUS的二次开发及在土石坝静、动力分析中的应用[J].岩土力学,2010(03):881-890.
[11]饶为胜,杜成斌,孙立国,等.基于环境激励的平原水库动力特性及动弹模反演研究[J].水利水电技术,2018,49(01):96-101.

