基于“全程分析”视角的物理习题教学探讨①

(安徽省绩溪中学,安徽 宣城 245300)

1 问题的提出

多过程问题涉及的物体运动过程较为复杂,涉及多个模型在时间和空间上的有机组合,涉及具有不同运动性质的多个运动阶段。这类问题具有综合性强、涉及知识面广等特点,适用于考查学生分析问题的程序性、逻辑性和严密性,侧重于考查学生的推理能力、建模能力、分析能力和解决实际问题的能力。[1]物理多过程问题的常规分析方法是分析物体运动过程,分析物体运动的每一个主要过程和变化,寻找过程之间的联系、运用相关物理原理列方程求解,将抽象复杂的物理问题变得形象具体,多过程问题常常会用到复杂的递推公式、等差等比数列、三角函数、不等式等,如果学生对每个过程都仔细分析,虽可以训练学生的推理能力、思维能力,但这个过程耗时长,计算过程繁琐冗长,阻碍了学生思维的发散和创新意识的提升。笔者采用“全程分析”的方法，处理多过程问题,简化物理模型,以提高学生科学思维能力。

2 “全程分析”的特点

“全程分析”是通过审题，了解物体运动的全过程,画出物理情景图并建立运动模型,从全过程的视角分析引起过程变化的因素,选择合适的处理方法，从整体的角度简化运动过程,得出综合性物理结论,其目的就是省略中间繁琐的递推、累加、数列推导、物理运算等处理过程。

“全程分析”是把不同运动性质的物体或不同运动阶段视为一个有机整体,考虑其在运动全过程的特点、运动的原因或产生的结果,从整体和全程的角度，把具有相互联系、相互制约、相互影响、相互作用的多个物体、多个运动状态、多个变化过程进行组合、研究。有时会从全过程的角度分析某一个力的作用积累效果,如全过程的总冲量、全过程力所做的总功等。有时会从全过程的角度分析总能量的变化,而不是对每一个分过程都要考虑,如小球多次与地面或墙壁碰撞损失的总机械能、子弹多次穿过木板损失的总机械能等。在物理教学中要善于运用“全程分析”的方法解决问题,达到知识的融会贯通,将物理问题化繁为简、变难为易,有效提高学生分析、解决问题的能力,有利于学生科学思维水平的提升,落实核心素养的培养目标。

3 “全程分析”应用实践

3.1 全过程物理量的累积效果

例1：质量为m的物体静止在光滑水平面上,从t=0时刻开始受到水平力的作用。力的大小F与时间t的关系如图1所示,力的方向保持不变,求3t0时刻的瞬时功率以及t=0到3t0这段时间内水平力的平均功率。

图1

解析：本题考查牛顿运动定律、匀变速直线运动、功和功率等相关物理知识,要求学生具备读图、识图、处理图形信息的能力。学生很容易明确该物体的运动是由两段匀变速直线运动组成的,由图1可以计算出两段运动的加速度,运用匀变速直线运动的速度公式和位移公式,先求出2t0时刻的速度,再求出3t0时刻的瞬时速度、两段运动的位移,进而可以求解出功率。毫无疑问,这种解法较为繁琐,容易出错,特别是本题只给了两段,如果是三段、四段,甚至更多,可想而知这个计算量是非常巨大的。

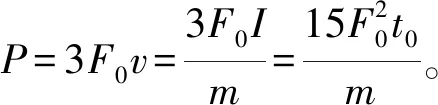
3.2 全过程整体的不变量

例2：一辆列车的总质量为M,在平直的水平轨道上以速度v匀速行驶,突然最后一节质量为m的车厢脱钩,假设列车所受的阻力与车的重量成正比,机车的牵引力不变,当脱钩的车厢刚好停止运动时,前面列车的速度为多大？

解析:本题的常规解题方法是：(1) 根据车在平直的水平轨道上匀速行驶，可求出恒定的牵引力。(2) 对脱钩车厢和剩余车厢分别做受力分析,运用牛顿第二定律求出两者的加速度。(3) 确定脱钩车厢和剩余车厢的运动性质是匀变速直线运动,分别应用匀变速直线运动的规律列方程求解,结合两个运动所用时间相等,联立以上的方程，可解出脱钩的车厢刚好停止运动时前面列车的速度值。这一方法的特点是所研究的对象多、方程多、转换多,计算过程也比较繁琐。

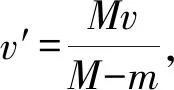
3.3 全过程运动图像的应用

例3：如图2所示,在光滑水平地面上有一质量为M的小车,其左端放有一质量为m的重物(可视为质点),m=2M,重物与小车之间的动摩擦因数为μ。开始时,小车和重物以共同速度v向右运动,一段时间后,小车与墙发生弹性碰撞,小车足够长,可保证重物和墙不相碰,当小车与墙壁第1次碰撞后,求重物相对小车能够继续运动的时间。

图2

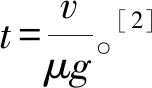
图3

4 结语

采用“全程分析”的方法，从全过程和整体的角度分析、处理多过程的物理综合性问题,避开分过程繁琐的递推、累加、数列推导等环节,引导学生从全局进行探究,培养学生的推理能力、建模能力、分析能力、发散性思维和创新能力,有效提高学生的问题解决能力，达成物理学科核心素养的培养目标。