基于Adam 优化神经网络的电梯群控算法
雷 剑
(南华大学 电气工程学院,湖南 衡阳 421000)
0 引言
电梯群控系统,通常是指在高层建筑内集中收集呼梯信号并管理调度3 台以上电梯的运行控制系统。目前电梯群控系统中,大多采用并联或者全集选的调度方法。这些方法依托于候梯时间等单目标优化方法,不能很好的同时解决候梯时间和运行效率的问题。20 世纪90 年代,基于BP 神经网络的电梯群控技术已经成熟运用到实际应用中,取得了很好的成绩[1]。但传统BP 神经网络还存在一些缺陷,如收敛速度不理想[2],难以脱离局部极值。由于BP 神经网络本身的结构和特性,网络模型效果最优的隐含层神经元个数无法确定[3],学习率以及激活函数的选择都会对神经网络的学习精度产生较大的影响。
电梯群控系统是一个存在多目的性、不确定性、非线性以及扰动性的复杂系统,同时包含着若干部电梯以及不同楼层之间的呼梯信号的庞大数据,这些都是传统电梯群控算法难以高效率、低能耗解决的问题。Adam(adaptive moment estimation,自适应矩估计)算法不仅适合解决含大规模数据和参数的优化问题,而且收敛速度更快、效果更好,能够更好的实现电梯调度分配,提高系统的整体性能。
1 电梯群控系统模型
1.1 多目标优化评价函数表达式建立
函数表达式选用了一种综合评价函数,作为某一楼层对某一台电梯呼梯的依据。通过满意度评价函数来弥补原本单目标优化电梯群控的不足。评价函数满意度的大小表示了电梯的呼梯次序。详细计算方法参看文献[4]。
公式(1)为第i部电梯与第j层呼梯信号之间的满意度评价函数[5]。
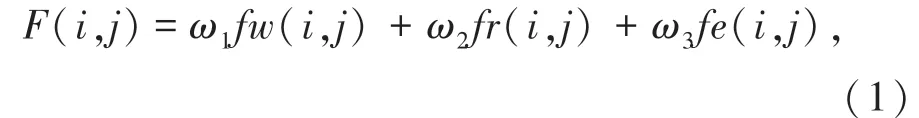
式中,ω1、ω2、ω3为评价函数中不同交通模式下的权重,权重之和为1。评价函数fw(i,j)为乘客平均候梯时间表达式;fr(i,j)为长时间候梯率表达式;fe(i,j)为能源消耗表达式。
1.2 电梯群控系统模型的搭建
1.2.1 BP 神经网络的模型搭建
模型中神经网络分为3 层结构,其中当前电梯内乘客数量、电梯到呼梯楼层的相对距离和电梯响应呼梯信号前需要停靠的楼层数,作为输入层的3个输入;隐含层是网络连接的核心,应根据具体情况建立相应模型;输出层只有一个神经元,作为某台电梯对当前呼梯信号满意度的输出。
网络训练中权值和阈值的修正过程如下:
(1)初始化网络的权值和阈值。
(2)向网络提供可学习的样本数据。

公式(2)表示,对于神经网络中第k 层的第i 个神经元的输出。S为真实数据,f(x)、g(x)分别为各个神经元以及输出层的激活函数。

(3)计算上一层神经元的输出,作为下一层的输入:(4)计算各层的学习误差,对于输出层有k=m:

得到误差后,在网络中进行反向传播。根据目标函数值的大小,以此对BP 网络进行训练。
(5)修正权值和阈值:
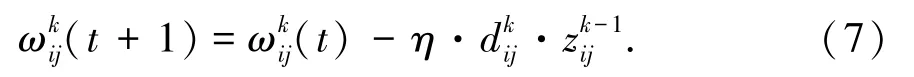
为了使模型尽可能得到好的收敛效果,在网络训练修正参数的过程中,增加学习率η,从而调节网络模型训练速率:

每组样本数据的学习得到最新修正的权系数后,判断预测值与实际值之间的相对误差是否满足预设目标。如满足则训练结束,否则返回步骤(3)。
1.2.2 Dropout
训练学习中,如果参数多,而训练样本少时,模型很容易发生过拟合的现象。Dropout[6]可有效缓解过拟合的发生,在一定程度上达到正则化的效果。
Dropout 是指在前向传播过程中,为了增强模型的泛化性,让某个神经元以特定的概率停止工作,进而缓解过拟合的发生。工作流程如图1 所示。
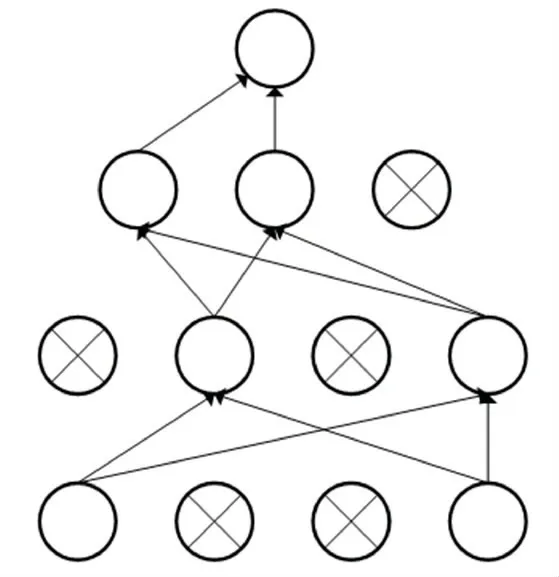
图1 引入Dropout 的神经网络模型Fig.1 Introducing the neural network model of Dropout
具体学习过程如下:
(1)训练前隐含层的所有神经元,以一定概率停止工作(暂时),不参与前向传播。输入输出神经元保持不变。
(2)样本数据在改变后的网络中前向传播,得到的误差再通过修改的网络进行反向传播。每次迭代后,在原来的神经网络上按Adam 算法更新权值和阈值。
(3)重复执行以上两个步骤,直至完成迭代训练。
Dropout 在随机选择神经元停止工作时,网络结构也会发生变化,而不同的神经网络模型也会产生不同的过拟合。其中互为“反向”拟合相互抵消,从而在整体上减少过拟合的现象,以此提升预测准确性。对三层BP 神经网络模型来说,Dropout 的超参数概率p设为0.2-0.4 比较合适,不会因此让损失函数的值过大,可有效减少测试集的误差。
1.2.3 电梯群控算法
Adam 算法是一种基于低阶自适应的随机目标函数一阶梯度优化算法[7]。由于该算法中包含了AdaGrad 算法和动量法的优点,以此训练得到模型的实际应用效果,在大多数场景下都要更优。其迭代过程如下:
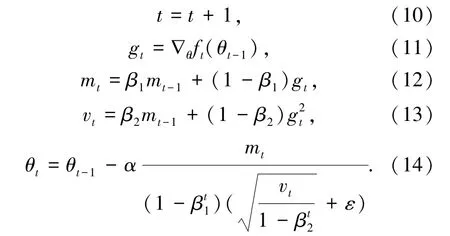
上述推导公式中,t为迭代数;α为学习率;默认设定为0.001;gt为计算梯度;公式(11)、(12)中,mt、vt分别为偏一阶矩向量和二阶矩向量。参数向量初始化:m0=0、v0=0;β1、β2分别为对应矩估计的指数衰减率,通常β1=0.9、β2=0.999;ε为一个非常小的正数,通常取ε=10-8,防止运算过程中出现分母为0 的现象。公式(14)中,θ即为待求的网络参数。
在确定了参数和目标函数之后,网络训练中循环迭代地更新各个参数,直到目标函数满足设定精度或达到预先设定次数为止。Adam 算法不仅易实现,并具有很高的计算效率,适合解决带有大规模数据和多个目标优化的问题。因此,本文选用Adam算法,作为基于神经网络的电梯群控系统的优化算法。
2 模型训练与测试
2.1 训练流程
BP 神经网络容易过早陷入局部极值且收敛速度较慢。因此本课题采用Adam 替代传统优化算法,并在网络的前向传播过程中加入Dropout,缓解过拟合的发生,有效增强了神经网络的泛化能力和收敛性。训练流程如图2 所示。流程步骤如下:
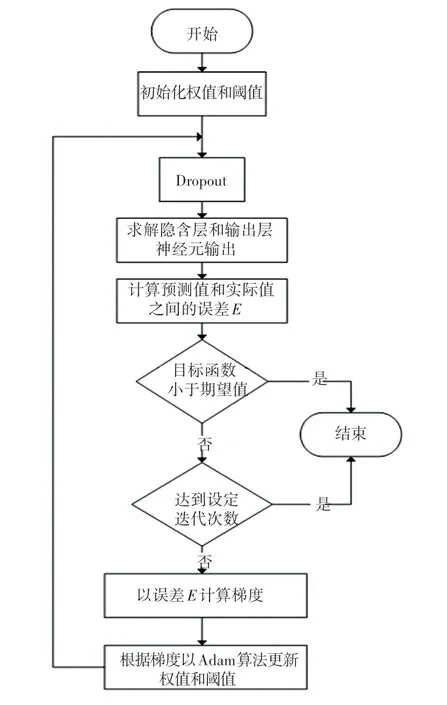
图2 基于Adam 算法优化BP 神经网络训练流程Fig.2 Optimization of BP neural network training process based on Adam algorithm
(1)根据样本数据计算多目标评价函数表达式,得到满意度函数值,再按照电梯群控系统要求建立神经网络模型。
(2)对网络的权值和阈值进行均匀分布初始化。
(3)在数据开始训练前,Dropout 以概率p随机停止网络模型中神经元的工作。
(4)以样本数据训练网络,求解网络预测值和实际值的误差E,将误差在网络中反向传播。
(5)根据误差求出目标函数的梯度,用Adam 算法修正网络的权值和阈值,直到目标函数小于期望值或者达到设定迭代次数,则退出训练;否则返回步骤(3)继续执行。
2.2 模型参数
模型中,需对以下4 个参数进行调优。其主要目的是让目标函数在满足设定精度的基础上,不断提高预测准确率。
(1)目标函数。目标函数是网络预测值与实际值的平均相对误差率,设定精度e <5%。
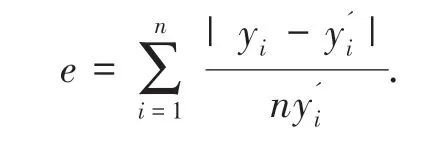
(2)学习率。网络中用SGD 以及Adam 两种算法进行比较。SGD 算法学习率设为0.01,Adam 算法学习率设为0.001。
(3)神经元个数与激活函数的选择。隐含层神经元个数一般采用实验法确定,为了神经网络能够得到最好的输入输出的映射关系,同时损失函数和输出误差满足期望要求,需要通过实验测定一个最佳的隐含层节点数。依据文献[8]的经验公式,可估算神经元个数的范围在3-12 之间。先设置数量较少的神经元个数进行训练,然后逐渐增加,使用同一样本集训练,最终选取网络误差最小时对应的隐含层节点数[9],见表1。

表1 神经元个数与激活函数的选择对误差的影响Tab.1 The Influence of the Number of Neurons and the Selection %
从表1 中可以看出,当隐含层神经元个数为8、激活函数为Sigmoid 时,平均相对误差最小。
(4)网络初始化。网络中的参数初值采用均匀分布初始化的方法。使用TensorFlow 提供的tf.random_uniform 函数,默认取值范围为[0,1],可以有效的减少梯度弥散问题,使得输入信号在网络中传递的更深。
2.3 模型的仿真与测试
在TensorFlow 框架中用Spyder 对神经网络进行搭建、训练与仿真。网络模型结构为三输入一个输出,隐含层层数为1,神经元个数为8。把经过统计的300 组电梯样本数据和对应的满意度评价值随机分成训练集和测试集并进行归一化处理,训练集包括290 组样本数据,其余10 组作为网络模型的验证的测试集。
图3 为基于BP 神经网络评价函数测试集平均相对误差结果对比。在条件相同的情况下训练1 000 次,每25 次取一次结果。结果表明,基于Adam 算法优化的网络平均相对误差e <2%,传统SGD 方法训练耗时10.716 S,而Adam 算法仅耗时8.634 S,收敛更加迅速。误差结果:随机梯度下降法平均相对误差为11.96%;Adam 算法平均相对误差为1.60%。
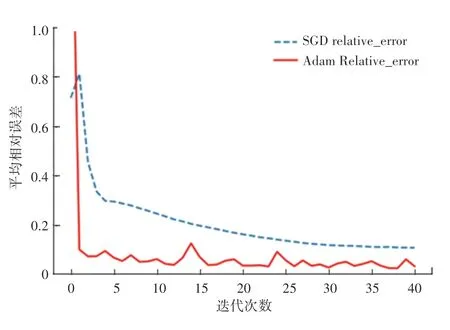
图3 神经网络拟合评价函数对比两种算法平均相对误差示意图Fig.3 Schematic diagram of comparing the average relative error of the two algorithms on the neural network fitting evaluation function
由图4、图5 可见,在测试集上预测结果表明:基于Adam 优化神经网络的算法误差更小,相比较传统 BP 传统神经网络,真实值和预测值的相对误差减小一个数量级,网络预测精度有明显的提高。
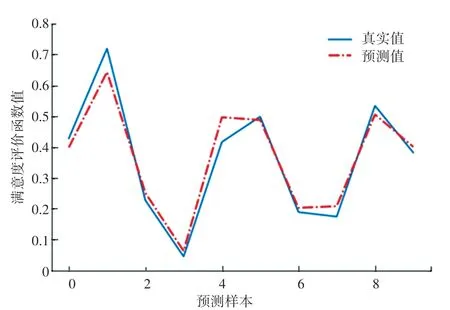
图4 基于传统BP 神经网络测试集满意度评价函数结果Fig.4 The result of satisfaction evaluation function based on traditional BP neural network test set
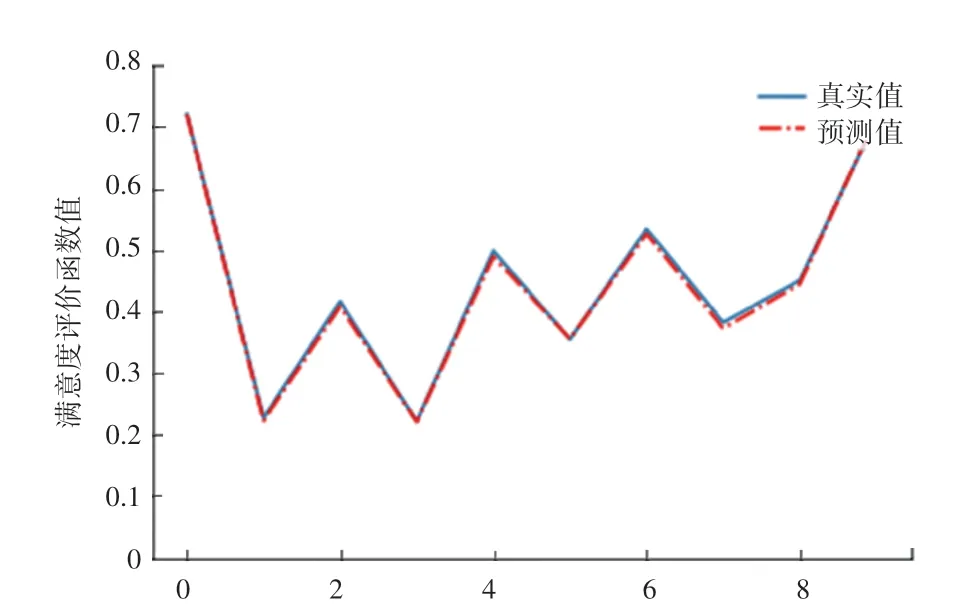
图5 基于Adam 优化神经网络测试集满意度评价函数结果Fig.5 The result of satisfaction evaluation function based on Adam optimized neural network test set
表2 中数据为基于Adam 优化神经网络测试集样本真实值和预测值的详细结果。从表中可见,最大相对误差为2.50%,最小相对误差为0.08%。整体测试集平均相对误差为1.26%,远小于传统SGD算法训练后的误差结果。

表2 测试集在Adam 优化神经网络模型的测试结果Tab.2 Test set results based on Adam optimized neural network model %
3 结束语
针对BP 神经网络的电梯群控传统算法的收敛速度慢,且易于陷入局部最小值,导致出现聚集效应、群控系统效率不高等问题的课题研究。首先在前人的基础上介绍了一种基于神经网络的多目标优化模型,在网络模型中将样本数据分别在基于传统随机梯度下降法的BP 神经网络与基于Adam 算法的BP 神经网络下各自学习,通过仿真测试验证效果。从表1 中的神经元和激活函数的组合搭配中可以看出,神经元个数和激活函数的选择会对网络的预测结果造成一定的影响,根据误差最小值选择为神经元个数为8,激活函数为Sigmoid,以此进行网络的学习训练和预测。但训练过程中出现了训练集效果很好,而测试集误差偏大的现象,因此在网络前向传播过程中加入了Dropout,一定程度上缓解了过拟合现象的发生,提高了预测的准确率。基于表2 的测试结果可以得出,Adam 算法优化后神经网络模型不仅收敛性更强,训练速度更快,同时更易于挣脱局部极值的束缚,提高了网络输出的准确率。在以多目标优化的基于神经网络的电梯群控系统的基础上改善了电梯运载效率,达到了优化目的,提升了整体电梯群控系统的性能。

