基于GWO-SVR 的冠心病住院费用预测

张 慧，贺 松，张 硕，黄 旭，席欢欢

（1 贵州大学 大数据与信息工程学院，贵阳 550025；2 贵州大学 医学院，贵阳 550025）

0 引言

随着健康中国战略的不断推进，人们更加注重医疗卫生建设，全面提高全民健康水平已成为各方关注的焦点。但就目前来看，中国医疗费用持续攀升，“看病难，看病贵”依然是医疗卫生事业改革的痛点和难点［1］。冠心病是全球死亡率最高的疾病之一，据世界卫生组织2011 年的报告指出，中国的冠心病死亡人数已列世界第二位，且发病呈年轻化趋势［2］。因此，研究冠心病住院费用的增长趋势，分析影响病人住院费用的显著影响因素，运用机器学习算法对住院费用进行精准预测，对协调提升全民健康水平和合理控制医疗费用增长具有重大意义。

支持向量机（Support Vector Machine，SV 是M）对于非线性问题具有较强的拟合能力，简单且泛化能力好，有较强的鲁棒性［3］。但通常在选取最优核函数时，存在许多随机性，经常无法达到良好的预测效果［4］。目前常用的参数优化算法主要有：差分进化算法（Genetic Algorithms，DE）［5］、粒子群优化算法（Particle Swarm Optimization，PSO）［6］和布谷鸟搜索算法（Cuckoo Search，CS）［7］等。本文采用2014年Mirjalili 等提出的灰狼算法GWO（Grey Wolf Optimizer）［8］，对SVM 回归模型进行参数优化。相较于上述几种优化算法，灰狼优化算法无论在参数寻优速度方面，还是在预测住院费用拟合效果上都具有突出表现。

1 理论方法

1.1 GWO 优化算法

1.1.1 基本原理

GWO 优化算法的本质就是模拟大自然灰狼群体中严格的等级制度和狩猎行为。通过把灰狼群体划分成α、β、δ、ω4 个等级，向猎物进行前进搜索，并依次作为最优解、次优解、次次优解和底层进行数学建模的过程。如图1 所示。

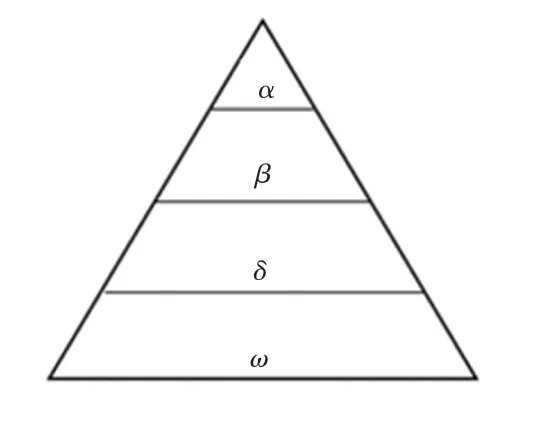
图1 GWO 灰狼群体等级分类Fig.1 GWO grey Wolf group classification

1.1.2 GWO 优化算法狩猎过程

GWO 优化算法是一种通过模仿狼群包围、追捕、攻击3 大步骤而形成狩猎行为过程。

（1）包围猎物。当灰狼一旦发现猎物，便会迅速向猎物靠近。灰狼与猎物间的距离以及灰狼位置的更新可由式（1）、式（2）得到。

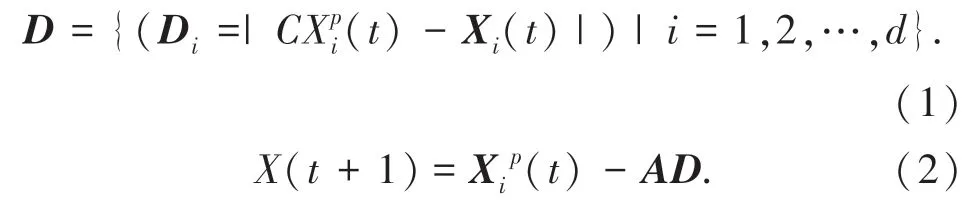
式中，d代表搜索空间维度；t代表灰狼当前的迭代次数；X（t）代表第t代灰狼位置向量；XiP（t）代表第t代猎物所在位置向量，即全局最优解向量；D代表灰狼与猎物之间的距离向量，A和C代表的是系数向量，由式（3）～式（5）得到。

式中，tmax代表最大迭代次数；a在迭代过程中线性从2 下降至0；r1与r2均为［0，1］上的随机变量。

（2）追捕猎物。狼群进行狩猎行为，通常是按照其适应度大小进行排序。可以依次获取到α 狼的位置，即最优解Xα；β 狼的位置，即次优解Xβ；δ狼的位置，即次次优解Xδ。

α、β、δ、ω 灰狼的实时位置更新公式由式（6）～式（8）得到。

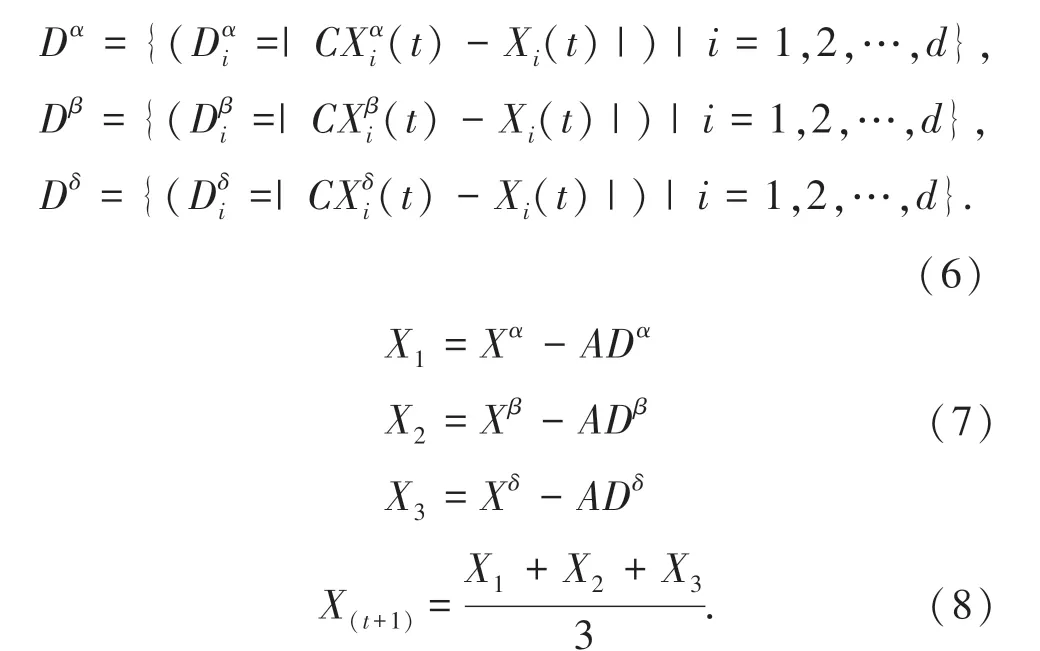
式中，X1、X2、X3依次代表灰狼α、β、δ 的实时更新位置，X（t+1）代表更新后的最优解向量。灰狼算法最优解的更新过程如图2 所示。

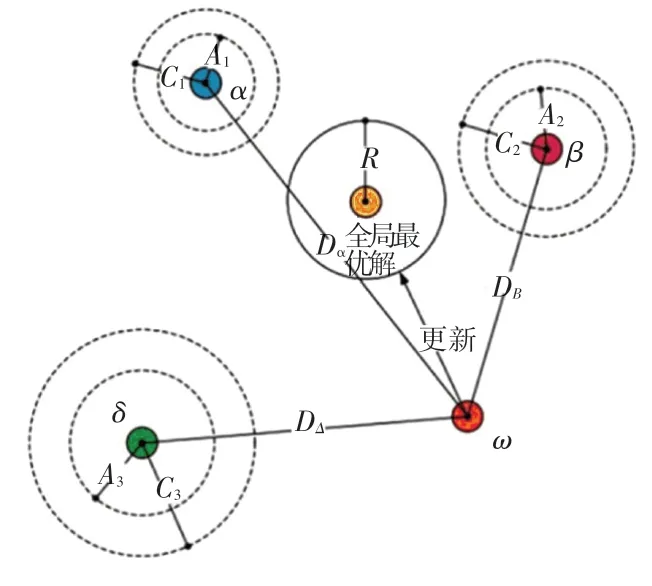
图2 GWO 算法最优解向量更新过程Fig.2 GWO algorithm optimal solution vector update process

（3）攻击猎物。当猎物停止移动时，灰狼便开始发起进攻。进攻行为的发起主要是通过式（3）中a迭代次数，从而间接控制式（4）中A的取值来完成的。当｜A ｜≤1 时，灰狼群对猎物进行攻击，对应局部搜索；当｜A ｜＞1 时，灰狼群将远离猎物散去，再次进行全局搜索。

1.2 支持向量机回归

支持向量机回归（SVR），是支持向量机（SVM）的重要应用分支之一，它是通过SVM 方法进行拟合曲线，做出相应的回归分析的模型［9］。其核心思想是寻找到一个回归平面，使得一个集合内所有的实验数据距离该平面的距离最近。

SVR 主要是通过给定不敏感损失函数ε，采用适合的核函数，进行样本训练。通过对惩罚因子c和核函数中的方差g的计算，获取到不为0 零的参数所对应的支持向量，继而通过训练样本进行建模，并利用该模型对测试样本进行预测的过程［10］。

式（9）中，ω代表权向量，b代表偏置向量。

式（10）中引入的是拉格朗日函数及松弛变量。C 代表SVR 模型的惩罚因子，用其来表达超出误差ε的惩罚程度；K（X，Y）代表SVR 模型的核函数。SVR 的回归模型由式（11）得到：

2 基于GWO-SVR 的预测模型构建

在SVR 回归预测中，惩罚因子c和核函数g的选取，将直接影响支持向量机的预测拟合效果。为进一步提高模型的准确率，需要借助灰狼优化算法，获取最优参数Bset_c 和Best_g，再进行SVR 回归预测。

GWO-SVR 预测模型的构建过程如下：

步骤1读取某二甲医院冠心病727 份病案首页数据进行预处理。按照比例随机划分数据集，最终生成650 份训练集数据和77 份测试集数据，并对所有数据进行归一化处理。

步骤2设置GWO 算法参数。种群规模设置为N，最大迭代次数设置为T；设定惩罚系数C和核函数方差g取值范围。

步骤3初始化狼群位置，即每个灰狼的个体位置均由惩罚系数c和核函数参数g的值决定。

步骤4计算每头狼相应的适应度，按照适应度函数值大小排序。

步骤5将灰狼群划分成α、β、δ、ω4 个等级。

步骤6根据公式（6）～公式（8）更新灰狼群中每个个体的位置；将灰狼新位置适应度与上一次迭代的适应度进行比较，判断是否替换适应度。

步骤7判断当前迭代次数是否为t≥T。若是，输出全局最优值Best_c 和Best_g；否则，跳转至步骤四，继续进行参数优化。

步骤8输出α灰狼位置，即得到最优的Best_c 和Best_g 参数。

步骤9通过最优的参数Best_c 和Best_g 建立SVR 回归模型，通过测试集进行预测，分析实验结果。

GWO-SVR 实现的流程图如图3 所示。

图3 灰狼算法优化SVR 参数流程图Fig.3 Gray Wolf algorithm to optimize the flow chart of SVR parameters

3 实验结果分析

3.1 数据来源

本研究选用了某二甲医院冠心病病人的病案首页数据，共计743 例。该数据能够最直观的反映冠心病病人在诊疗过程中最真实有效的费用。经过对目标样本进行数据清洗，缺失项填补、删除信息不全及不符合逻辑项共计16 例，共纳入有效项727 例，纳入率为97.84%。

3.2 住院费用影响因素分析

通过对727 份冠心病住院费的住院年份、患者年龄、入院途径、并发症合并症级别、是否手术等多个因素进行多重回归分析，结果证明：回归方程模型具有统计学意义（F＝545.336，P＝0.000），方程决定系数R2＝0.892。说明住院费用89.2%的变异可由表1 中9 个变量解释。其中对冠心病住院费用影响最大的前3 位因素分别为：是否造影检查、是否手术、特级护理时间。

3.3 数据预处理及参比模型

将727 份病案首页数据按照9 ∶1 的比例，随机划分成650 份训练集和77 份测试集数据。实验中将上述9 大显著影响住院费用的因素作为输入数据，将住院费用作为输出数据。由于医院病案数据因病人而异，变化幅度相对较大，有时具有突变性，而SVR 模型对［0，1］的数据又非常敏感，所以在建模之前，需要借助对病案数据进行归一化处理，以此来提高回归模型的效率。归一化方法如式（12）：

表1 住院影响因素的多重回归分析Tab.1 Multiple regression analysis of influencing factors of hospitalization

为了验证GWO-SVR 模型对冠心病住院费用预测的准确性和有效性，本文除了与原始SVR 模型形成对照外，还通过与差分进化算法优化的DESVR 模型、布谷鸟算法优化的CS-SVR 模型和粒子群优化算法的PSO-SVR 模型形成对照模型，进行了比较分析。

为公平起见，将SVR 参数取值范围设置为：c∈［1，100］，g∈［1，100］；所有优化算法的种群个数设为20，最大迭代次数设为20。其中，CS 的缩放因子上界为0.8，下界为0.2，交叉概率为0.2；PSO 的c1＝c2＝1.5。

3.4 实验结果分析

图4、图5 分别描述了在原始SVR 模型和GWO-SVR 模型下测试集的预测结果。

图4 SVR 模型下的预测集预测Fig.4 Prediction set prediction under the SVR model

图5 GWO-SVR 模型下的预测集预测Fig.5 Prediction set prediction under the GWO-SVR model

由图可以清晰地看到，在灰狼算法的优化下，SVR 回归模型能够更好的对预测集数据进行预测。为了验证本文所提出的GWO-SVR 模型的有效性和准确性。表2 给出了不同优化算法模型对惩罚因子Best_c 和核函数方差Best_g 的寻优结果。

通过均方误差MSE、决定系数R2、SVR参数迭代寻优时间T3 个指标，评价不同模型的回归预测性能。详尽数据见表3。

表2 不同优化算法下的Best_c 和Best_gTab.2 Best_C and Best _g under different optimization algorithms performance

表3 不同模型下的回归预测指标Tab.3 Regression prediction indexes of different models

通过表3 的结果可以发现，原始SVR 模型参数寻优速度较慢，而上述4 种优化算法均可以显著提升参数寻优速度；另外CS-SVR、PSO-SVR、GWOSVR3 种预测模型相较于原始SVR 模型，对均方误差MSE、决定系数R2都有一定的提升。而DE-SVR预测模型的均方误差和决定系数R2不降反升，有可能是参数设置原因，但参数寻优时间相较于原始SVR 模型被明显缩短。总体来说，本文所引入的的GWO-SVR 模型表现最佳，不仅使预测结果的均方误差最小，还具有较强的全局空间搜索能力，在SVR 参数寻优时仅需要1.16 s 就可以得到最理想的（c，g）解向量，决定系数R2相较于原始SVR 模型也具有最明显的提升，有效提高了冠心病住院费用的预测精度。

4 结束语

本文通过多重回归分析和归一化处理，分析出影响住院费用的显著影响因素的同时，又提高了SVR 模型对数据的敏感性，为进一步提高冠心病住院费用预测的精度。本研究引入灰狼算法，对支持向量机回归的惩罚因子C 和核函数方差g 进行进一步寻优，算法的全局搜索能力显著提升。GWO 可以迅速锁定SVR 中最优（C，g），因此在进行预测模型的搭建时，住院费用的预测结果得到了很大的提升。通过与原始SVR 模型、DE-SVR、CS-SVR、PSOSVR 的形成对照模型发现，基于灰狼算法优化的SVR 模型表现最佳，均方误差仅为0.004 0，参数寻优迭代速度最快仅需1.16 s、在决定系数R2上也由原来的0.865 2 显著提升至0.961 3。