2004-2015年新疆喀什地区百日咳的动力学建模与仿真
文静 王建鹏 王凯

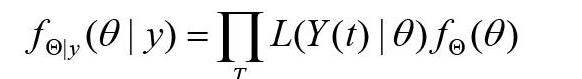
摘 要 目的:基于新疆喀什地区2004—2015年百日咳每年的新发病例数据,建立动力学模型来分析百日咳的传播规律,为喀什地区制定百日咳控制策略提供行之有效的定量参考依据。方法:根据百日咳的传播机制,使用传染病动力学建模方法构建百日咳动力学传播模型,使用马尔可夫蒙特卡罗算法(MCMC)进行模型参数估计和拉丁超立方抽样方法(LHS)进行模型参数的敏感性分析。结果:分析百日咳动力学模型,得到模型拟合结果[平均绝对百分比误差(MAPE=19.27%),均方根百分比误差(RMSPE=27.35%)]和基本再生数R0=11.5192[95%CI:11.4648-11.5727],说明新疆喀什地区百日咳已有成为地方病的趋势。通过模型参数敏感性分析看到,百日咳的传播率β、恢复率?酌和新生儿接种率p对百日咳的传播有着重要的影响。结论:新疆喀什地区百日咳新发感染數有上升趋势,有关部门应加强对高危人群的预防与检测,定期关注新疆喀什百日咳的传播与流行情况,适当扩大监测对象进而有效的预防和控制百日咳病情的进一步扩大。
关键词 动力学模型;参数估计;敏感性分析;疾病控制
中图分类号: O175;R516.6 文献标识码: A
DOI:10.19694/j.cnki.issn2095-2457.2020.02.049
0 引言
众所周知,百日咳(whooping cough或pertussis)是由一种百日咳鲍特菌(简称BP)感染所致的一种可以预防和治愈的严重急性呼吸道传染病。百日咳的传染性较强并且人群普遍易感。因此,百日咳的传播对人类的健康构成了威胁[1]。一个横断面的研究表明,现有的预防免疫控制策略对保护新生儿的作用不突出[2]。在1974年之后,全球就实施给新生婴儿接种百白破疫苗(diphtheria,tetanus and pertussis combined vaccine,DTP)的免疫计划,使得全球的百白破疫苗接种率达到了80%,致使百日咳发病率和死亡率急速下降,百日咳得到了非常有效的控制。但近些年,全球百日咳发病率又明显上升,甚至在有些疫苗接种率较高的英国、美国等国家出现了暴发或者流行的现象[3], 由此可见,百日咳是一种具有复发性的传染病。虽然百日咳可以通过接种疫苗来预防,但是接种过疫苗人群的免疫力也有一定的有效期,超过有效期的人群会回到易感的人群。
新疆地处边疆,疫苗的接种率低于全国的平均水平,这对新疆地区百日咳的患病率会有极大影响,依照疾病监测信息报告管理系统新疆百日咳2004-2012 年的疫情资料显示:百日咳发病总数为3760 例,死亡5例,年平均发病率为2.02/10万[4]。而喀什地处南疆地带,根据疾病监测信息报告管理系统新疆百日咳2004-2015年的喀什地区的数据显示:新疆喀什2004 年百日咳的发病人数为388人(发病率为11/10万人),到了2015年发病人数增加到526人(发病率为11.7/10万人),呈现了缓慢上升的趋势。因此,分析和掌握新疆喀什地区百日咳的流行趋势来预防百日咳成为地方病是非常有必要的。本文考虑百日咳在传播过程中的相关影响因素,建立了百日咳的传播动力学模型,为新疆喀什制定百日咳控制策略时提供行之有效的相关参考依据。
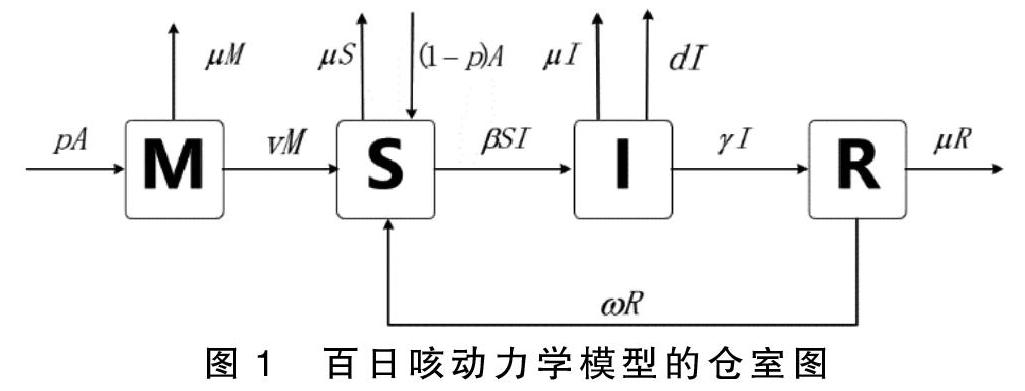
本文根据百日咳的传播规律,将人群分为注射百日咳疫苗的新生儿(M)、易感人群(S)、百日咳感染者(I)和患病后恢复者(R)4类,构建如下百日咳传播的仓室模型(如图1)。
2 模型应用
2.1 参数估计
首先,给出模型部分参数的确定值:(1)根据疾病监测信息报告管理系统2004-2012年新疆百日咳疫情资料,百日咳发病数为3760例,死亡5例[4],所以因病死亡率d取值为d=5/3760≈0.0013。(2)由文献[5]可知,新疆人口的预期寿命为71.12岁,所以自然死亡率μ=1/75≈0.0141。(3)如今,百日咳疫苗覆盖率提高到了以上[6],所以新生儿百日咳疫苗接种率。(4)根据文献[7]可知,新生儿在接种百日咳疫苗12年后,随着免疫力减弱仍有患百日咳的风险,所以取υ=1/12≈0.0833。在感染百日咳病恢复后具有的免疫力期限方面,资料中没有具体的说明,暂时估计感染百日咳病恢复后具有的免疫力期限为12年,所以恢复后免疫力减弱速速ω=1/12≈0.0833。
新疆喀什地区2004年百日咳新发病例数为388人,因此,M(t)的初始条件为M(2004)=388。假设其他初始值分别为M(0)=311679,S(0)=5000,I(0)=388,R(0)=350。
其次,根据模型(1)和马尔可夫蒙特卡罗算法(MCMC)来估计参数β和?酌。我们将累积病例建模为泊松分布的随机变量,因为泊松分布描述了在一段时间内观察到的事件的数量。我们通过采样校准模型参数的后验分布向量θ|y={β,?酌}|y,向量y源于Y(t)=βSI,Y(w)表示被报道的累积病例。我们用Metropolis-Hastings接受准则,通过马尔可夫链蒙特卡洛进行抽样。后验密度为
前密度fΘ(θ)是两个单变量的联合概率先验。我们认为β和?酌是基于U(0,1)的分布,程序可在R3.3.1版本中实现。我们从30000个迭代中采样,并将前200个样本作为一个老化周期样本去掉。在这28000个样本的基础上,计算出基本再生数R0的点估计值和的置信区间,并根据现有的参数值计算出三种分布对R0的贡献。结果如表1所示。
最后,计算出基本再生数R0=11.5192,其中R0的95%置信区间为95%CI:11.4648-11.5724,R0的取值范围具体如图2。
2.2 模型评价
用已建立的传染病动力学模型拟合新疆喀什2004-2015年百日咳的累积发病数,图3表明实际的累积发病数的点在曲线附近分布,并且置信带较窄,MAPE=19.27%,PMSPE=27.35%,MAPE与RMSPE均<50%,显示模拟结果比较合理,并且MAPE在19%-20%之间,且MAPE与RMSPE均<30%,说明建立的模型拟合效果良好。
2.3 模型参数敏感性分析与疾病控制
拉丁超立方抽样的不确定性和灵敏度分析已被广泛应用于传染病模型[9-11]。因此,为了检验模型的各个参数变化的敏感性,分析出各个因素对模型结果的影响程度,使用拉丁超立方抽样样本作为R0的样本参数[8]来计算基本再生数R0表达式中各个参数的偏秩相关系数(PRCC)值与P值。模型中各个参数的(PRCC)值对基本再生数R0的影响为:参数的PRCC值中绝对值中相较大的,对于基本再生数R0的变化影响更大。正号或负号分别表示影响是正或是负。本文选择样本大小n=1500,参数d,β,?酌,ω,μ,p和υ作为输入变量,R0作为输出变量。共计7个参数的PRCC值与P值如表2。表2 显示了因病死亡率d(PRCC=-0.8310)对R0有最大的影响,紧随其后的是净死亡μ(PRCC=-0.7845), 其次是患百日咳病率β、患百日咳病后的恢复率?酌、新生儿百日咳疫苗接种率p和接受百日咳疫苗的免疫力减弱速度υ。7个参数对R0的敏感性如图4所示。图4 显示了β和υ对R0有正面影响,而d,?酌,μ和p对R0有负面影响;同时看出,参数ω作为假设值,R0对ω不敏感(P>0.05),而其他参数均具有统计学意义。因此,从以上敏感性分析看到,从实际情况出发,控制百日咳的流行和传播最有效的方法是减少参数β的值和增加参数ω和p的值。
在上述工作的基础上进一步讨论参数β、?酌和p对R0的影响。控制其他参数不变的情况下,使用软件分别画出β与R0、?酌与R0和p与R0之间的关系变化图。
为了使R0保持在1e-06到5.42e-05之间,控制其他参数不变时,R0随着β变化的情况如图5所示。图5表明了R0随着百日咳的患病率β的增加而增加,患病率β的曲线与直线R0=1相交于点(4.7e-06,1)。则说明当百日咳的患病率β<4.7e-06的时候,可以采用控制百日咳的患病率的方法来有效控制百日咳的传播。
为了使患百日咳后恢复率?酌保持在1到20之间,控制其他参数不变时,R0随着?酌变化的情况如图6所示。图6表明了R0随着患百日咳病后恢复率?酌的增加而减少,恢复率?酌的曲线与直线R0=1相交于点(11.8,1)。则说明当患百日咳后的恢复率?酌>11.8时有R0<1, 可采用控制患百日咳病后恢复率的方法来控制百日咳的传播。
根据实际情况,新生儿的百日咳疫苗接种率p需控制在0到1之间,控制其他参数不变时,R0随着疫苗接种率p变化的情况如图7所示,图7表明了R0随着疫苗接种率p的增加而减少,从图中可看出,疫苗接种率p=1时,R0为11.34,也就是点(1,11.34),则说明即使疫苗接种率p增加到100%,R0的值也很大。从图7也可看出,疫苗接种率p对R0是有效的,但是并不是最有效的控制,这也与表2中的PRCC与p值相吻合。
综合以上考虑因素把减少百日咳的患病率、增加患百日咳病后的恢复率和增加新生儿的疫苗接种率相结合起来,就可以更加有效地控制百日咳的流行与传播。
3 讨论
百日咳对于新疆来说,在2004-2015年间每年发病率都有不同程度的上升趋势,而喀什地区是全疆地区百日咳发病情况的高发区[12],因此,喀什百日咳的流行和传播情况对全疆百日咳疫情都会有较大的影响。新疆喀什地区在2004-2015年间,百日咳每年平均发病率为4.73/10万人,这12年中2015年的发病率是最高的,高达11.7/10万人,在全疆位居前列。因此,为了研究新疆喀什百日咳的传播与流行情况,本文根据百日咳的发病机理构建传染病动力学模型,使用马尔可夫链蒙特卡罗算法(MCMC)估计模型参数β=5.42E-05和?酌=1.0116。算出了喀什地区的基本再生数R0=11.5192(95%CI:11.4648-11.5724),这表明百日咳在新疆喀什已经呈现出流行的趋势。通过模型拟合,拟合精确度指标与均,说明建立的模型拟合效果良好,具有一定的可信度。使用拉丁超立方抽样方法(LHS)进行模型参数的敏感性分析,结果表明百日咳的患病率β和患百日咳病后的恢复率?酌是影响百日咳传播与流行的主要影响因素,新生儿的百日咳疫苗接种率p是有效的控制因素但相比前两个参数不显著。
因此,本文给出如下一些控制新疆喀什地区百日咳疾病的措施:(1)降低百日咳的患病率;具体做法:新疆是温带大陆性气候,环境干燥,加之南疆的日照少,而喀什就处在南疆,那么可以通过适当的外出活动来提高免疫力。(2)提高患百日咳病后的恢复率;具体做法:提示医护人员在诊断中要提高警惕,百日咳的症状与普通感冒相似,应加强对百日咳的血清監测,及时发现和确定是否患百日咳病,以便于及时发现尽早隔离治疗,防止病情的恶化和传染给其他人。(3)增加疫苗的接种率;具体做法:百日咳是一种可以传染的疾病,但是是可以预防的,严重时还会导致死亡,新生儿可以通过接种疫苗来预防这种疾病的发生。至今为止,预防百日咳最经济有效的方法就是通过接种百日咳疫[13],所以应该提高新疆地区的百日咳疫苗接种率和全程接种率,定期进行百日咳疫苗的查漏补种工作,以此来降低百日咳的发病率。
综上所述,要完全控制或消灭百日咳的传播与流行是有一定难度的,因此,相关部门应做好预防措施,防患于未然,定期关注新疆喀什百日咳的传播与流行情况,适当扩大监测对象进而有效的预防和控制百日咳病情的进一步扩大。
参考文献
[1]张柳,赵建宏,张庶民.百日咳流行病学研究进展[J].中国疫苗和免疫,2008,14(6):559-564.
[2]徐勇胜.百日咳临床特征研究进展[J].中国实用儿科杂志,2016(9):712-715.
[3]许红梅,郑佳佳,XuHongmei,等.百日咳临床特点及流行病学研究进[J].中华实用儿科临床杂志,2014,29(22):1681-1682.
[4]陈涛,谢娜,甫尔哈提·吾守尔,等.2004-2012年新疆维吾尔自治区百日咳流行特征分析[J].疾病监测,2013,28(11):911-913.
[5]罗冬梅,吴顺华,王凯.新疆巴州地区梅毒的动力学建模与仿真[J].中华地方病学杂志,2017,36(7):542-546.
[6]Althouse B M,Scarpino S V.Asymptomatic transmission and the resurgence of Bordetella pertussis.[J].BMC Medicine,13,1(2015-06-24),2015,13(1):146.
[7]李树堂.成人也会患百日咳[J].大家健康,1996(12):16-17.
[8]Marino S,Hogue I,Ray C,Kirschner D.A methodology for performing global uncertainty and sensitivity analysis in systems biology. Journal of theoretical biology.2008;254(1):178-196.
[9]Blower S,Mclean A,Porco T,Small P,Hopewell P,Sanchez M,et al.The intrinsic transmission dynamics of tuberculosis epidemics.Nature medicine.1995;1(8):815-821.
[10]Blower S,Dowlatabadi H.Sensitivity and uncertainty analysis of complex models of disease transmission:an HIV model,as an example. International Statistical Review/Revue Internationale de Statistique.1994;229-243.
[11]Sanchez M,Blower S.Uncertainty and sensitivity analysis of the basic reproductive rate:tuberculosis as an example.American Journal of Epidemiology.1997;145(12):1127-1137.
[12]陳佳,谢娜,吴秀峰等.基于ARIMA乘积季节模型的新疆喀什百日咳流行趋势分[J].新疆医科大学学报,2017,40(3):380-384.
[13]BLACK RE,COUSENS S,JOHNSON HL,et al.Global,regional,and national causes of child mortality in 2008:a systematic analysis[J].Lancet,2010,375(9730):1969-1987.

