基于微气泡的巡飞弹翼展气动特性仿真与分析

邵伟平，孙 林，郝永平，裴乙橦，姬 曼

(沈阳理工大学 机械工程学院，沈阳 110159)

微致动器(Microactuator)是一类能够产生和执行动作的微机械元件或装置的总称，又被称为微执行机构或微驱动机构。在微机械系统的研究中，微致动器是非常重要的一部分，它的主要作用是通过一些物理原理将其他形式的能量转化为机械能，并能使整个微机械系统正常运行。目前，微致动器主要广泛应用于国防、医学、生物、航空航天等领域。

美国加州大学洛杉矶分校的研究人员率先提出微气泡致动器的想法，并将其安装在机翼表面上，并结合三角翼周围气流流动的特点，利用微气泡致动器来控制和操纵翼面上的边界层，从而能够进一步来实现对三角翼飞行器动态转矩控制，并初步取得较理想的实验结果[1]。在我国，陆鹏举教授和吕宗行教授讨论和研究了采用微模拟技术制作的微气泡致动器对弹体气动力的影响控制。微气泡致动器根据弹性体的几何形状附着在弹性体的表面上，以高压气源作为动力来源，在预定情况下为微泡充气，并做了相关实验，并得出结论：当微气泡致动器同时位于强涡流区和弱涡流区并处于工作状态时，可以在适当条件下削弱由气流引起的侧向偏移；当微气泡致动器只在强涡流区工作时，气泡鼓起会对气流边界层产生影响，并导致边界层上的分离涡提前分离；当微气泡致动器只在弱涡流区工作时，气泡鼓起会使气泡区域形成剪切层，并产生较大的剪切力，加大弱涡流区的涡流强度[2]。

本研究将气泡型微致动器安装在巡飞弹机翼上表面，当不需要微气泡工作时，气泡不鼓起且与机翼上表面平齐；当需要微气泡工作时，巡飞弹内部气缸给气泡充气，使其鼓起变形，从而达到对气流产生影响并干扰打破机翼上表面原有边界层的作用。

1 模型建立及计算网格的生成

数值模拟分析方法是一种不用具体的函数表达式而是用多个点的数值表示函数的方法，利用科学计算机来求解建立的数学模型的近似解。将数值模拟分析方法与CFD(Computational Fluid Dynamics——计算流体力学)相结合，解决各种离散化的数学模型，同时模拟分析处于复杂环境中的流体力学问题[3]。

通过对巡飞弹特性及外形的精确选择，可以对巡飞弹基本形态(状态1)进行建模，为研究气泡对巡飞弹的影响，本研究将在巡飞弹的基本形态的基础上，选取翼面上表面气泡完全鼓起为状态2；选取右侧翼面上表面气泡完全鼓起，但左侧翼面气泡未鼓起为状态3，如图1所示。

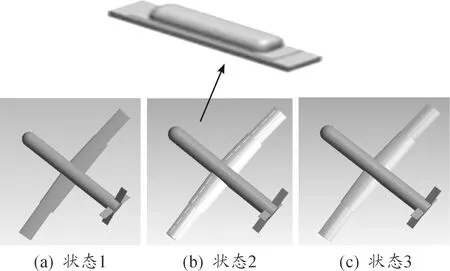
图1 翼型状态

对模型进行网格的划分是计算流体力学的第一步，网格质量通常决定了模拟的效果或收敛速度，直接涉及气动数值模拟的仿真精度。本研究网格采用非结构化网格，为尽量使仿真结果误差较小，采用的是密度较大的网格，压力进口边界与压力出口边界都是无穷远，且无滑移壁面[4]。通过使用Gambit软件，首先对巡飞弹流体域进行网格划分，然后划分整个流场的计算域，并将其划分为多个子区域，同时需要确定每个子区域的节点，这样可以将巡飞弹的计算域变为多层，使得网格的质量得到提高，如图2所示。在网格分布设置方面需要以巡飞弹为中心网格以一定的比值由密集变为稀疏，可以提高巡飞弹所受的升力、阻力以及力矩值的精度。

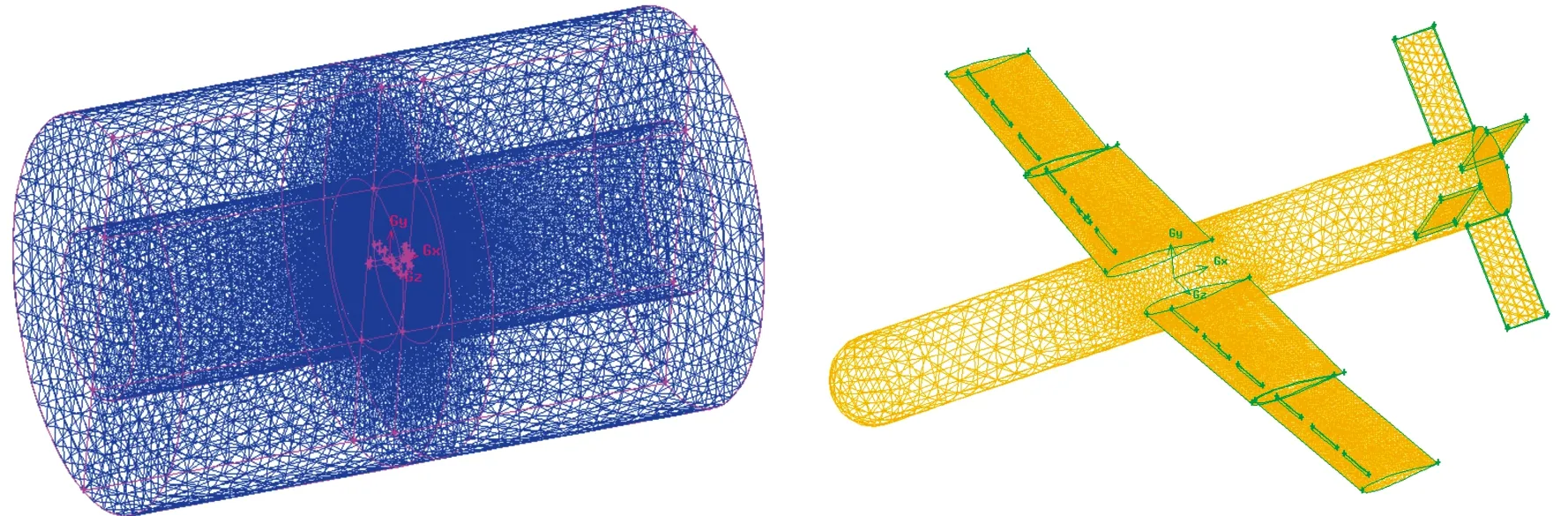
图2 流体计算域及网格生成示意图

Fluent是目前国际上比较流行的商用CFD软件包，凡是和流体热传递和化学反应等有关的工业均可使用，并广泛应用于航空航天、汽车设计、涡轮机设计等方向，所以采用Fluent进行模拟仿真，并进行相关参数设置：在设置求解器的时候选择密度基隐式计算函数方法，可以加快收敛速度，同时选取适合非结构化网格的Green-Gause Node Based计算方法[5]。并选取适用于空气动力学的湍流模型——Spalar-Allmaras模型为湍流模型。控制器的松弛系数为0.3，库朗数为2，通量方法为Roe-Fds，迎风格式为二阶迎风式。

2 气动特性结果分析

2.1 阻力系数对比分析

状态1为巡飞弹基本飞行状态；状态2为微气泡全鼓起状态；状态3是右侧微气泡全鼓起，左侧气泡未鼓起。

首先分析侧滑角为0°时不同马赫数下不同状态的阻力系数，得到阻力系数随攻角的变化曲线如图3所示[6]。在同一马赫数下，巡飞弹的阻力系数的分布图大致以0°攻角相对称。

由图3(a)可知，当Ma=0.7时，巡飞弹的阻力系数先是随攻角的增加而减小，然后随攻角的增加而增大。在攻角为-4°～12°之间时，状态1的阻力系数要比其余两种大11.7%～22.8%，且状态3的阻力系数最小；当攻角为8°和大于12°时，3种状态的阻力系数几乎持平。

由图3(b)当Ma=0.9时，在负攻角段，飞行器的阻力系数先是随攻角的增加而减小，到达正攻角阶段随攻角的增加而增大。当巡飞弹飞行攻角为负时，状态1 的阻力系数最小，而当攻角为正时，状态1的阻力系数反而比其他两种状态大，最大可比状态2高23%；状态3的阻力系数始终处于状态1和状态2之间。

由图3(c)当Ma=1.5时，在状态1、2、3情况下，飞行器的阻力系数先随攻角的增加而减少。在攻角小于4°时，状态1的阻力系数最小，能比状态3低 15%左右；当攻角大于4°时，三种状态的阻力系数几乎一致。

由图3(d)当Ma=3.0时，依旧状态1的阻力系数最小，状态2的阻力系数最大；也就是说明就阻力系数这一项来说，巡飞弹在超音速情况下飞行时，气泡不但不能减小阻力系数，反而增加12%～30%。

图3 状态1、2、3在不同马赫数下的阻力系数曲线

2.2 升力系数对比分析

侧滑角为0°时不同马赫数下不同状态的升力系数随攻角的变化曲线如图4所示。以下对不同马赫数下的升力系数变化规律逐一分析。

由图4(a)可知，当Ma=0.7时，升力系数随攻角的增加而上升。当攻角小于0°时各个状态升力系数相差不大；当攻角大于0°时，状态3的升力系数最大，而状态1的升力系数最小，当攻角为8°时，状态3所提高的升力系数最大，为27%。

由图4(b)可知，当Ma=0.9时，气泡未鼓起到自然态(状态1)时的升力系数先随攻角的增大而升高，到攻角为12°时随攻角增加而降低，则当攻角达到12°左右时，该状态达到失速，12°攻角也就被称为失速攻角；而气泡鼓起到自然态(状态2、3)时的升力系数在攻角为20°内一直是随攻角的增加而升高，且状态3的升力系数在任何状态下都比其他两种状态高[7]。

由图4(c)可知，当Ma=1.5时，气泡未鼓起到自然态(状态1)时先随攻角的增加而上升，当攻角达到12°时随攻角的增加而降低，此攻角为失速攻角。而气泡鼓起到自然态(状态2、3)时，升力系数一直是随攻角的增加而升高，在仿真攻角内，并未达到失速状态，表明气泡可以调整翼面绕流，从而提高了此飞行器的失速攻角。此外，状态2、状态3在同一攻角下的升力系数几乎相等。

由图4(d)可知，当Ma=3.0时，各个状态的升力系数随攻角的增加而上升，状态1和状态2的升力系数相差不大，状态3的升力系数在攻角大于8°时与状态1、2相差不大，但当攻角小于8°时，状态3的升力系数要比其他两种状态大。

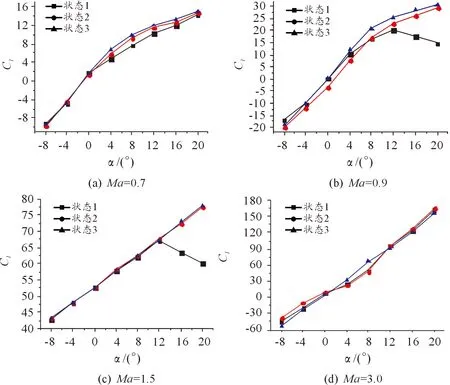
图4 不同马赫数下的升力系数曲线

2.3 升阻比对比分析

侧滑角为0°时不同马赫数下不同状态的升阻比随攻角的变化曲线如图5所示。以下对不同马赫数下的升阻比变化规律逐一分析[8]。

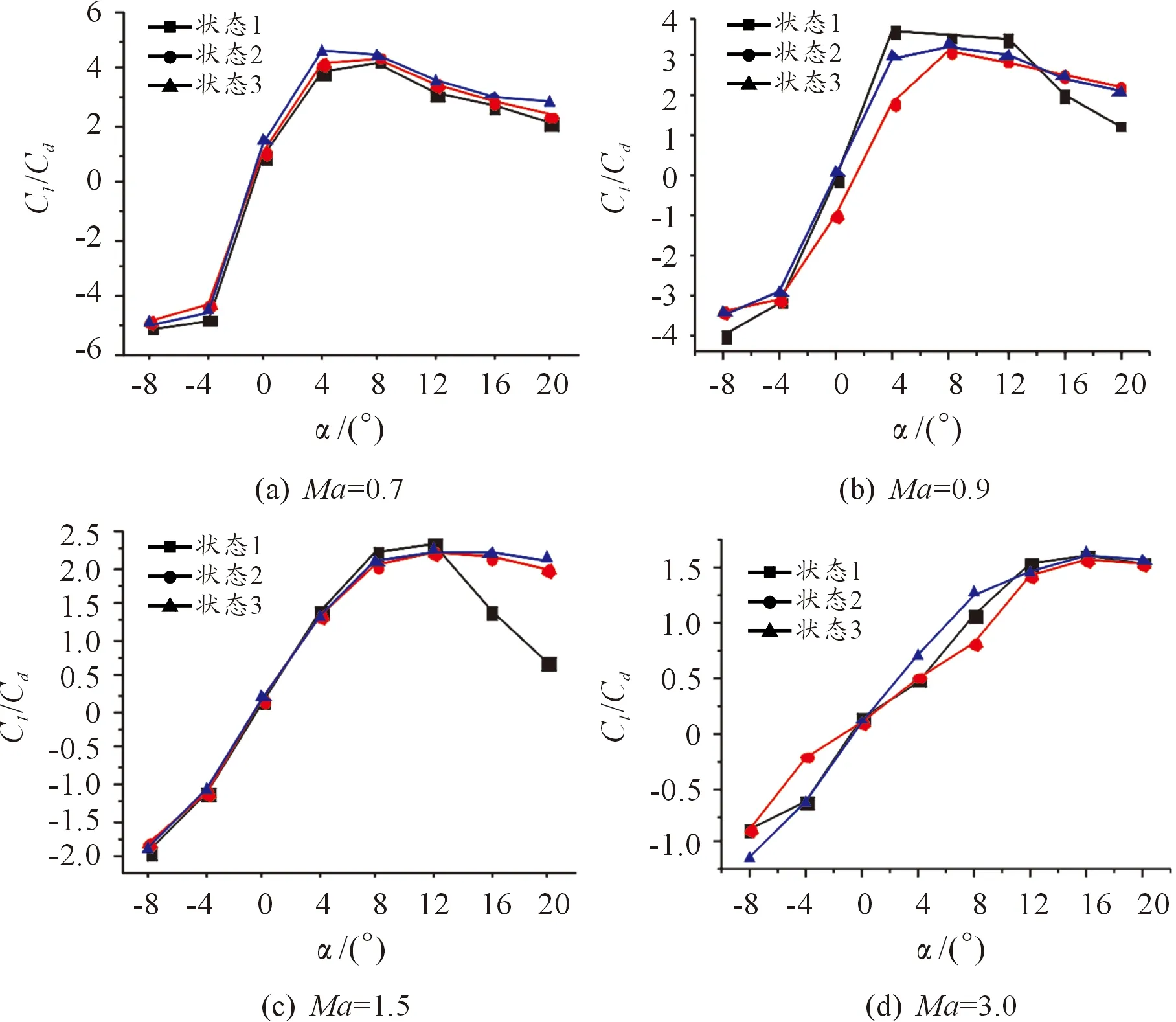
图5 不同马赫数下的升阻比曲线

当Ma=0.7和0.9时，升阻比的变化趋势大体上相似，且都是先随攻角的增加而增加，达到一定攻角后逐渐降低。当Ma=0.7时，状态1的升阻比要比其他两种状态小；当Ma=0.9时，状态1的升阻比在攻角小于12°时要比其他两种状态大，而当攻角超过12°之后，状态1的阻力系数反而要小于另外两种状态；当Ma=1.5时，状态1的升阻比先随攻角的增大而增大，但达到一定攻角时随攻角的增大而减小，而状态2、3的升阻比一直随攻角的增加而升高；当Ma=3.0时，各个状态的升阻比均随攻角的增加而升高。

3 巡飞弹翼面截面压力分布云图及分布曲线

3.1 不同状态下的飞行器翼面截面压力分布

图6为状态1、2、3在α=0°、β=0°、0.9Ma条件下的飞行器翼面截面压力分布云图及压力分布曲线。

由图6可知，在马赫数、攻角、侧滑角相同的情况下，机翼上气泡鼓起到自然态(状态2、3)时的压力差要大于气泡未鼓起到自然态(状态1)。状态1情况下，机翼上下表面压力相差不大；状态2和状态3情况下，机翼下表面的压力要远高于上表面的压力。在状态2、3的云图上可知，机翼上表面气泡后面会产生一个低压区。

3.2 不同马赫下的飞行器翼面截面压力分布

图7为状态2在α=0°、β=0°不同马赫条件下的飞行器翼面截面压力分布云图及压力分布曲线。

由图7可知，在相同状态、同一侧滑角、同一攻角的情况下，1.5马赫的压力要远大于0.9马赫下的压力，但是上下翼面的压力差相差不多，在机翼上表面气泡后面会产生一个低压区[9]。在1.5马赫下机翼前缘会产生较大压力的激波，但在0.9马赫下机翼前缘会产生很大面积的高压区。

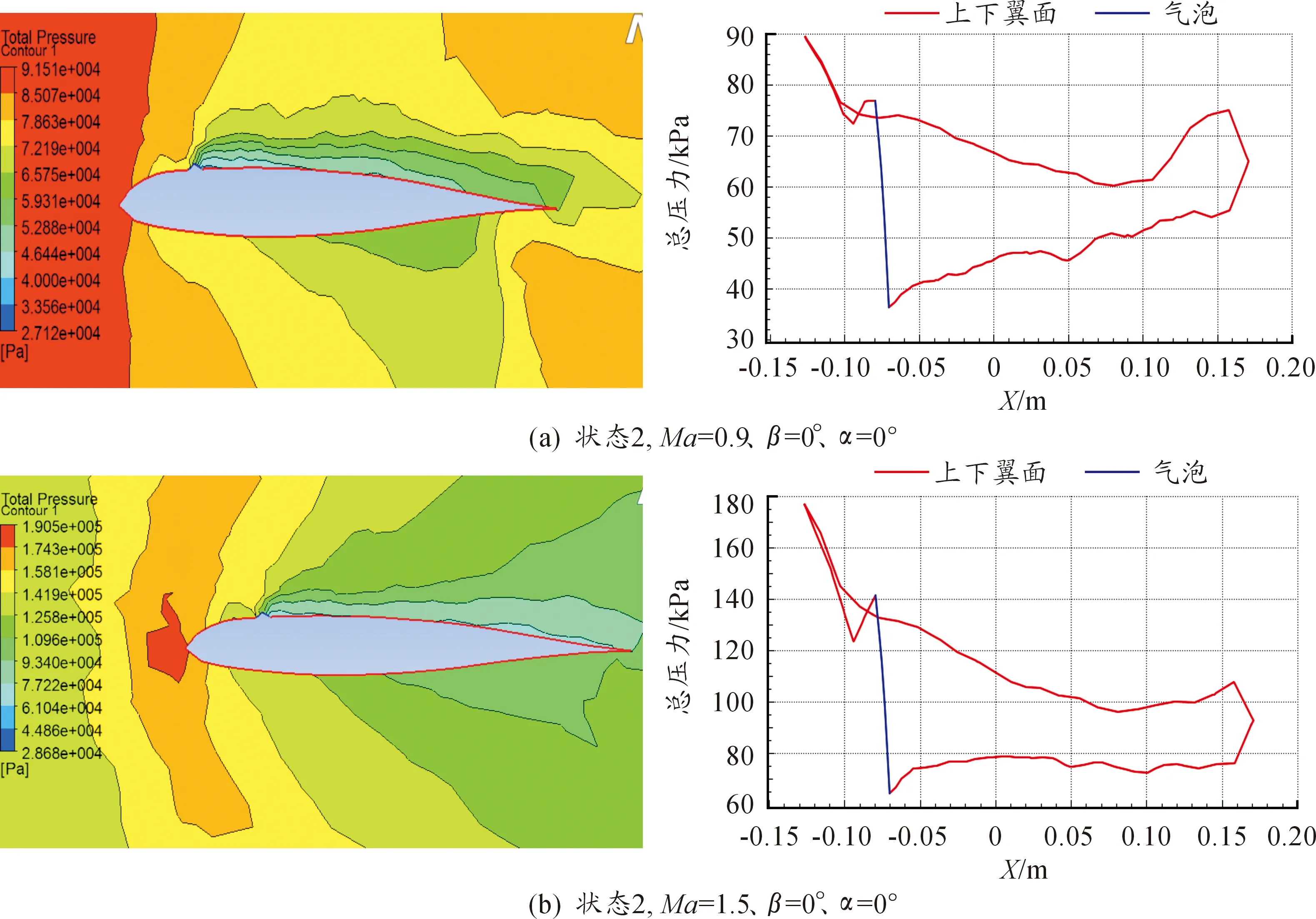
图7 不同马赫下飞行器翼面截面压力分布云图及压力分布曲线

4 结论

对3种基于气泡的巡飞弹翼展的气动特性仿真，绘制出不同状态气动特性系数的变化曲线，得知各状态的气动特性变化趋势虽大致相同，当气泡完全鼓起到自然状态时，由阻力系数变化曲线可知，当速度为0.9Ma，攻角为12°时，阻力系数可降低23%；由升力系数变化曲线可知，当攻角大于12°时，气泡型巡飞弹的升力系数比普通型巡飞弹高；由云图可知，气泡的鼓起能延缓气流分离泡的分离时间，在一定程度上提高巡飞弹的失速攻角。