商合杭高铁钢-混凝土连续结合梁设计
杨欣然, 左家强, 万明
(中国铁路设计集团有限公司,天津 300308)
1 工程概况
商合杭高铁古城特大桥主要为跨越西淝河、黑茨河、谷河、京九铁路、省道308、界阜蚌高速公路等工点而设。茨谷河是黑茨河右岸的支流河道,刘庙湾以上河段称南八丈河,刘湾庙以下河段称谷河,古城特大桥在DK145+726.00 处小角度跨越茨谷河,采用5×50 m钢-混凝土连续结合梁跨越。
钢梁与混凝土桥面板结合而成的组合钢箱梁因其抗扭能力强、整体性好及更能适应大跨与特殊要求的特点,获得了较大发展[1-4]。德国海德明登跨越维拉河谷(80+2×96+80+64) m 公路桥、(44.7+64+72.8+72.8+64+44.7)m 伍珀河谷高速公路大桥均采用组合钢箱梁[5]。组合钢箱梁国外主要应用在公路上,我国近年来在铁路上的应用取得了许多成果,2003 年建成的秦沈客专修建了14座钢-混凝土连续结合梁,2004年建成通车的津滨轻轨采用1 孔跨度50 m 简支钢-混凝土结合梁[6-7]。但应用于时速350 km 高速铁路无砟轨道,商合杭高铁跨越茨谷河5×50 m钢-混凝土连续结合梁为我国首次。
商合杭高铁5×50 m钢-混凝土连续结合梁主要技术标准如下:
(1)设计速度:350 km/h。
(2)线路情况:双线,线间距5.0 m,平面线形为直线,竖向有纵坡。
(3)轨道类型:CRTSⅢ型板式无砟轨道,轨顶至梁顶高738 mm。
(4)地震烈度:地震基本烈度Ⅶ度,动峰值加速度0.1g。
(5)气象资料:桥位处年平均气温14.8 ℃,历年极端最高气温41.4 ℃,历年极端最低气温-20.4 ℃,最冷月平均气温0.8 ℃,最热月平均气温27.8 ℃。
2 主要荷载
2.1 恒载
(1)结合梁纵向计算时钢结构截面只考虑主截面和纵向加劲肋,横隔板及竖向加劲肋以集中力的形式施加,焊缝及螺栓等的质量按照1.1 倍的增大系数考虑;混凝土桥面板按其实际质量考虑。
(2)结合梁混凝土桥面板收缩作用:桥面板预制板存梁时间要求不少于6 个月,预制段按降温-10 ℃、现浇段按降温-15 ℃考虑。
(3)结合梁混凝土桥面板徐变作用:结合梁设计采用换算截面法,根据钢和混凝土弹性模量比(简称弹模比)将2种材料换算成钢进行计算,由于混凝土的徐变效应,需再根据荷载效应的不同对弹模比进行折减[8-9]。经过初步设计阶段按各结合梁规范计算结果的对比分析,施工图设计采用Q/CR 9300—2018《铁路桥涵设计规范(极限状态法)》规定,恒载(永久作用)作用下弹模比取18.0,活载作用下弹模比取12.2,温差作用下弹模比取14.0。
2.2 活载
(1)结构纵向计算采用ZK 标准荷载,横向计算及局部构件检算采用ZK特种荷载。
(2)活载动力系数取值研究。
古城特大桥为高速铁路钢-混凝土连续结合梁桥,TB 10002—2017《铁路桥涵设计规范》未根据高速铁路桥梁类型进行区分,关于高速铁路钢-混凝土结合梁动力性能试验研究的相关文献较少。按照TB 10002—2017《铁路桥涵设计规范》中冲击系数的计算公式(古城特大桥L=50 m,Lφ=75 m),计算结果差异明显。
普速铁路简支或连续钢梁:
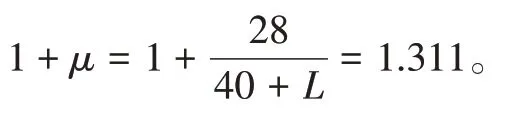
普速铁路钢-钢筋混凝土板结合梁:
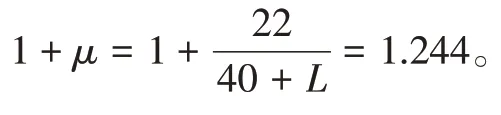
高速铁路:
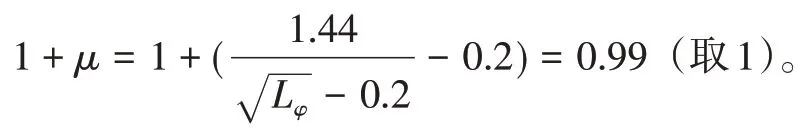
刘鹏辉等[10]对 1 联 (40+56+40) m 钢-混凝土连续结合梁进行动力试验,试验列车为:CRH2 动车组(250 km/h)、内燃机车+弓网检测车+轨道检查车+隔离客车组成(160 km/h)、货运列车(120 km/h)共3 类。试验结果表明,3类试验列车作用下的动力系数均小于设计动力系数1.275(按TB 10002—2017《铁路桥涵设计规范》普速铁路钢-钢筋混凝土结合梁公式计算)。李运生等[11]研究得出行车速度越大,钢-混凝土结合梁动力响应越明显的结论。
日本《铁道构造物等设计标准及解说钢桥、结合梁桥》规定的动力系数计算公式为:

针对古城特大桥,Ka取1(参考新干线取值),v取350 km/h,L取50 m,经计算μ=0.407。对于双线桥梁应乘以α,因此本桥动力系数为1+μ=1.305。
古城特大桥设计速度350 km/h,综合以上分析,动力系数按TB 10002—2017《铁路桥涵设计规范》中普速铁路简支或连续钢梁的计算公式计算。
2.3 温度作用
(1)整体升降温:合龙温度按(15±5)℃设计,结合梁整体升降温按±25 ℃考虑,钢梁与混凝土板间的材料温差采用±15 ℃,整体升降温和材料正负温差组合叠加采用。
(2)日照温差:参照TB 10092—2017《铁路桥涵混凝土结构设计规范》附录B执行。
(3)箱梁横向计算的温度荷载分日照和寒潮2 类,温度荷载图式见图1。
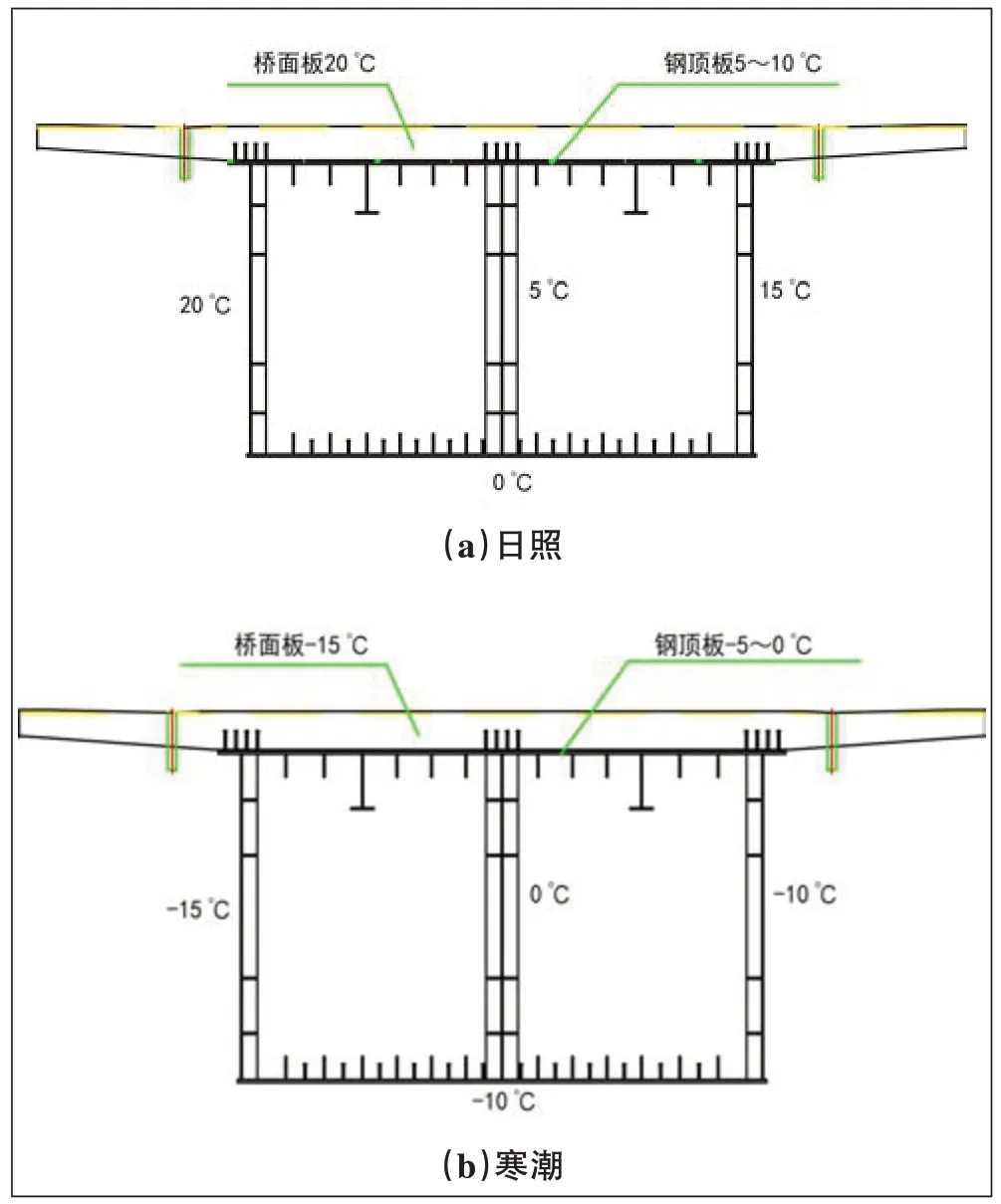
图1 温度荷载图式
3 结构构造
3.1 主要材料
(1)钢梁材质采用Q370qE,钢材技术条件应满足GB/T 714—2008《桥梁用结构钢》要求。
(2)预制桥面板采用C55混凝土,桥面板湿接缝及剪力钉槽采用C55 补偿收缩混凝土,底板及隔墙采用C30混凝土。
(3)钢梁与混凝土桥面板用柔性剪力钉连接,钢梁顶板布置了φ22×220 mm 剪力钉,底板布置了φ22×170 mm剪力钉。
3.2 截面形式
5×50 m 上承式连续结合梁钢梁截面为单箱双室闭口钢箱梁,梁高3.585 m,底宽6.8 m。钢箱梁顶、底板厚20~32 mm,腹板厚16~20 mm,顶板沿纵向设连续U形肋,底板沿纵向设连续板肋,腹板设T形竖向加劲肋和连续水平加劲肋,竖向加劲肋间距为1 m;钢箱内沿纵向每隔4 m 设1 道横隔板,2 片横隔板之间设置一道底板T形横肋,与腹板的T形竖肋连接成为U形横肋。
钢箱梁顶通过剪力钉与混凝土桥面板连接为整体,混凝土桥面板中间厚度43.0 cm (预制桥面板为41.5 cm+1.5 cm 环氧树脂砂浆层),悬臂端部厚度25.0 cm,混凝土桥面板全宽12.6 m。
钢-混凝土结合梁截面中心处全高4.015 m,为了降低截面重心、增强梁体稳定性、提高行车安全性,钢箱梁箱底铺设30 cm厚混凝土,通过剪力钉与钢底板连接。经计算,设置箱底混凝土后,结合梁截面重心由距梁底3.44 m降低到2.70 m。根据车桥耦合动力仿真分析,铺设底板混凝土后桥梁位移响应相差不大,桥梁加速度响应略有减小。桥梁各跨竖向和横向振动位移较小,竖向和横向振动加速度均小于规范规定限值,说明古城特大桥振动性能良好,行车舒适性达到优良水平。结合梁横断面见图2。
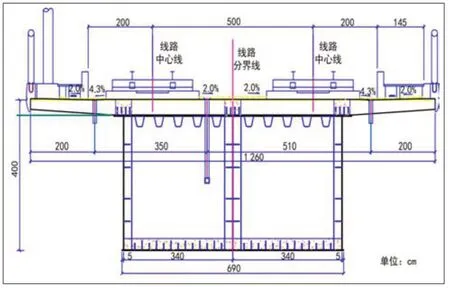
图2 结合梁横断面
4 结构设计
4.1 纵向计算模拟
刚度分配法如下[5]:

式中:Is为钢梁对自身截面形心的惯性矩;Io为换算截面惯性矩;Ao为换算截面面积;Ms为钢梁承担的弯矩;Mc为混凝土板承担的弯矩;M为梁的总弯矩。
为验证有限元模型中结合梁的内力、应力与公式计算的结果是否一致,分别建立双单元模型和联合截面模型,按照作用均布荷载进行对比。结果显示:采用双单元模型建立的结合梁模型,提取钢梁弯矩Ms和钢梁轴力Ns,按照式(2)计算得出的总弯矩M与联合截面模型结果误差最大在10%以内,截面最不利位置处的弯矩误差在5%以内。可见,采用双单元模型模拟结合梁,结合梁内力分配给钢梁和混凝土与式(2)计算存在很小误差,故采用双单元模型模拟结合梁能够满足要求。
4.2 纵向内力放大系数
连续结合梁钢箱内布置了箱底混凝土,除降低结合梁重心外,也会参与受力,为了避免遗漏可能发生的不利影响,计算时考虑以发生最大内力来假定截面刚度。具体做法如下:
假定1:求解正弯矩区截面最大内力时,不考虑负弯矩区的混凝土桥面板刚度,考虑正弯矩区底板混凝土刚度,将负弯矩区刚度设定为“钢梁+钢筋+底板混凝土”刚度,正弯矩区刚度设定为“钢梁+桥面板+底板混凝土”刚度。
假定2:求解负弯矩区截面最大内力,全区间(包括负弯矩区)计入桥面板截面刚度,同时不考虑正弯矩区底板混凝土刚度,将负弯矩区刚度设定为“钢梁+桥面板+底板混凝土”刚度,正弯矩区刚度设定为“钢梁+桥面板”刚度。
假定3:结合梁结合后采用的截面刚度,不考虑正弯矩区底板混凝土刚度和负弯矩区桥面板刚度,故负弯矩区刚度设定为“钢梁+钢筋+底板混凝土”刚度,正弯矩区刚度设定为“钢梁+桥面板”刚度。
结合梁计算采用假定2进行建模,通过表格进行负弯矩区刚度处理(负弯矩区刚度换算成“钢梁+钢筋+底板混凝土”刚度)、内力处理(内力根据刚度进行分配)。
根据假定1、假定2 刚度组合建立MIDAS 模型,计算出正弯矩区内力放大系数,结合梁模型中将恒载乘以最大放大系数进行设计。
4.3 混凝土桥面板及钢箱梁翼缘有效宽度
Q/CR 9300—2018《铁路桥涵设计规范(极限状态法)》钢-混凝土组合结构部分、《铁路钢-混凝土结合梁设计规范》报批稿、TB 10621—2014《高速铁路设计规范》附录C 均有箱梁有效宽度的折减系数计算方法;日本铁路规范仅规定了作为组合截面的受压翼缘板的有效宽度,没有规定连续梁支点上方混凝土板的有效宽度计算方法。通过计算比较,采用TB 10621—2014《高速铁路设计规范》附录C计算有效宽度对结构受力更为不利。
4.4 负弯矩区处理
与简支结合梁不同,连续结合梁负弯矩区混凝土桥面板将承受拉力,对于负弯矩区混凝土桥面板受拉的处理是设计难点,一般有桥面板施加预应力、采用高配筋方案控制裂缝宽度、负弯矩区钢与混凝土采用抗拔不抗剪连接等几种处理措施。
(1)古城特大桥设计过程中对桥面板施加预应力的方式进行了分析,采用先安装跨中范围混凝土桥面板后安装支点处的施工顺序,以减小跨中桥面板自质量对支点负弯矩的影响。不同混凝土板浇筑顺序组合结构内力见表1。可见,钢梁正负弯矩区弯矩均增大,混凝土负弯矩区拉应力可由2.75 MPa降低为1.05 MPa。

表1 不同混凝土板浇筑顺序组合结构内力
(2)经过不同顶升顺序、不同顶升高度并结合桥面板浇筑顺序进行计算比选,古城特大桥采用2个中墩顶升0.60 m 和2 个次中墩顶升0.20 m。中墩采用较大顶升量是为保证中墩支点桥面板施加足够大的压应力,次中墩顶升量较小是根据成桥后4个桥墩支点桥面板压应力相当确定。钢梁及混凝土板应力情况见表2,支点顶升及混凝土桥面板安装顺序示意见图3。

表2 钢梁及混凝土板应力情况 MPa
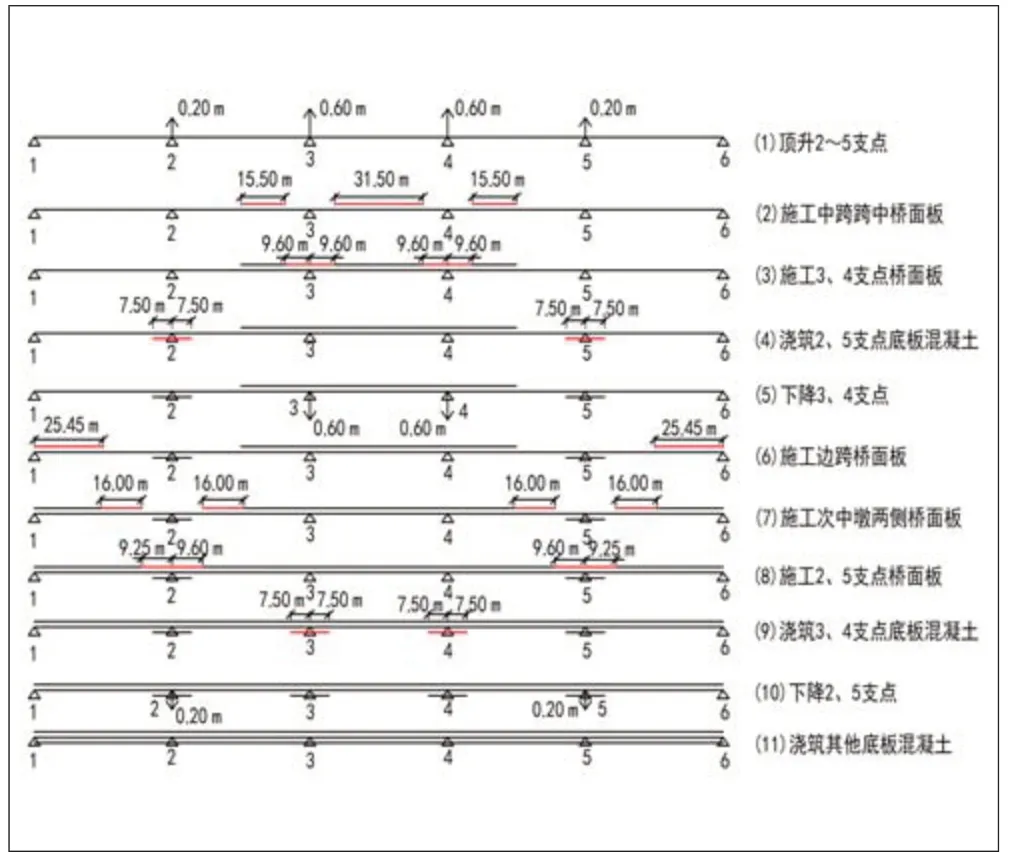
图3 支点顶升及混凝土桥面板安装顺序示意图
高配筋方案施工简单,受力明确,通过配置一定比例钢筋能有效限制裂缝宽度,在极限状态下能有效抵抗外荷载,且在国内外已成功应用。因此古城特大桥不设置预应力束,采用高配筋方案,桥面板范围内配置3 排HPB400 钢筋,直径25 mm,横截面方向间距100 mm,截面配筋率为3.65%,钢筋拉应力为87.68 MPa,裂缝宽度为0.14 mm,能够满足规范要求。
在采用以上技术措施后,负弯矩区混凝土桥面板裂缝满足规范要求,因此古城特大桥不采用抗拔不抗剪剪力连接件,进一步提高了结构耐久性。
4.5 结构动力性能
随着列车运行速度的不断提高,对桥上线路的平顺性也提出了更高要求。钢-混凝土连续结合梁在温度荷载作用下,桥面必然会发生变形,进而影响线路平顺性,会对高速列车运行的安全性、舒适性造成不利影响。因此进行车桥耦合动力仿真分析时,将全桥温度变形曲线叠加到轨道高低不平顺中,考虑温度对桥上线路不平顺性的影响。全桥温度变形曲线见图4,轨道不平顺曲线(叠加全桥温度变形曲线)见图5。
通过对古城特大桥在CRH2、CRH3 型动车组作用下的车桥空间耦合振动进行分析,列车以设计速度运行时,行车安全性和乘坐舒适性达到“优”或“良”的水平,说明古城特大桥动力性能良好。

图4 5×50 m钢-混凝土连续结合梁温度变形曲线

图5 轨道不平顺曲线(叠加全桥温度变形曲线)
5 结束语
依托商合杭高铁古城特大桥5×50 m钢-混凝土连续结合梁,对结构的静动力性能进行了分析,确定了适用于结构特性的计算模型、活载动力系数、钢梁和混凝土板的有效宽度,通过调整施工顺序和支点顶落梁等措施对负弯矩区混凝土板施加预压力,有效控制了负弯矩区混凝土裂缝宽度。随着商合杭高铁全线通车,5×50 m钢-混凝土连续结合梁运营状况良好,可对我国结合梁的发展起到推动作用。

