三种求根方法的比较

温智琦

摘要：实践中，求解方程得出的近似解必须有着必要的精度，也就是说求解方法必须使得近似解可以精确到小数点后任意位。求解方程近似解时，运用二分法、牛顿迭代法和不动点法，实际上是使用了算法的思想，可以解决一些一元多次方程和无理数方程、超越方程等问题。

关键词：二分法   牛顿法   不动点法   迅速求根   收敛

函数是因变量关于自变量的对应关系，方程是函数的基础上，求解特定自变量的等式。

对于一些简单的方程，我们可以用公式法求得精确解[1]。但对于高次方程、超越不等式、隐函数方程等很难在理论上求出精确的解。在实践中的目的是寻求方程的近似解。那么，求解方程近似解的方法便成为了必须要解决的问题。而且，求解得出的近似解必须有着必要的精度，也就是说求解方法必须使得近似解可以精确到小数点后任意位。

求解方程近似解时，运用二分法、牛顿迭代法和不动点法，实际上是使用了算法的思想，可以解决一些一元多次方程和无理数方程、超越方程等问题。

一、二分法

（一）二分法的概念

首先，引入零点存在定理：在区间上连续并且端点值异号的函数在这个区间上一定存在零点[2]。

根据零点存在定理可以得出求解方程近似解的二分法——即一分为二的方法。

若函数y=f（x）在区间[α，b]上连续，并且f（α）*f（b）<0，可以通过把函数f（x）的零点所在的较小的区间分成两部分，然后选择根所在的那个区间，继续二分该区间，逐步迭代，使区间越来越小。当区间的两个端点的精确度足够时，任一端点均可作为近似解。这就是二分法的精髓。

（二）二分法举例

以方程 x4+x3+2x2-3=0为例。

（1）尝试选取x1=1，x2=-1。将x1=1 与x2=-1代入函数f（x）=x4+x3+2x2-3，即可得f（1）=1，f（-1）=-1;

（2）f（x1）与f（x2）异号，所以直接进入下一步。否则重复第一步，直到找出f（x1）与f（x2）异号的结果;

（3）将x1与x2两者的平均数x3代入函数f（x），也就是将x3=0可得f（x3）=-3<0;

（4）f（x3）=-3<0，令x1=x1，x2=x3;否则令x1=x3，x2=x2，然后回到步骤（1），循环这个步骤[3]。

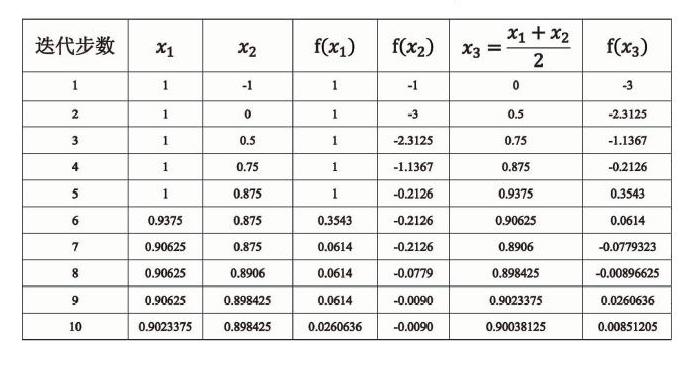
我们将迭代使用的近似根列在下表中：

这样，十步迭代之后，我们可以得出该方程的一个近似根在（0.898425，0.90028125）之间。

二、牛顿法

（一）牛顿法概念

牛顿法又称为牛顿迭代法、牛顿-拉弗森方法[4]。牛顿法是把非线性方程在局部小区间线性化的近似方法。把f（x）在点x0的某邻域内展开：

取其线性部分（即泰勒展开的前两项），并令其等于0，即

，以此作为非线性方程f（x）=0的近似方程，若               ，则其解为                        ，同理可得：

（二）牛顿法举例

仍以方程x4+x3+2x2-3=0为例。

（1）尝试选取x1=1。将x1=1代入函数f（x）=x4+x3+2x2-3 ，即可得f（1）=1;

（2）求     ;

（3）即    ;

（4）令x1=x2，回到步骤（1），循环这个步骤。

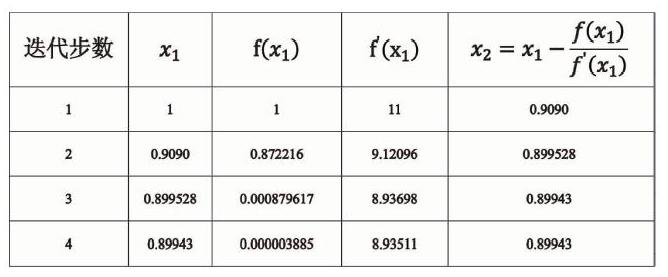
我们将迭代使用的近似根列在下表中：

这样，经过三步迭代之后，我们已经得到该方程的一个近似根在0.89943附近。

（三）牛顿法局限性

举一个例子：            。

首先，嘗试选取x1=1;则                                             。则x2

。然后，继续令x1=-2;则

我们发现，首先选取的根为1，第二步迭代后为-2，但是第三步迭代后的根为4.0028，这在（-2，1）的范围外。显然可知，

的根为，在（-2，1）的区间之内。所以，牛顿法具有局限性，对于某些方程，可能无法快速算出有效的结果。

三、不动点法

（一）不动点法概念

不动点原理是泛函分析中最重要的一个原理之一，它依据于著名的巴拿赫压缩映射[5]。

由方程f（x）=0构造方程g（x）=x。其中g（x）是连续函数。若x=x*是方程f（x）=0的根，则其肯定也满足g（x*）=x*，x*是函数g（x）的不动点（之一）。

构造迭代公式

这就是不动点迭代法，若该式满足                     ，则x*是函数g（x）的一个不动点，即方程f（x）=0的一个根。

（二）不动点法举例

仍以方程 x4+x3+2x2-3=0为例。构造函数                  。然后，

（1）尝试选取x1=1，则                                    ;

（2）令x1=x2，回到步骤（1），循环这个步骤。

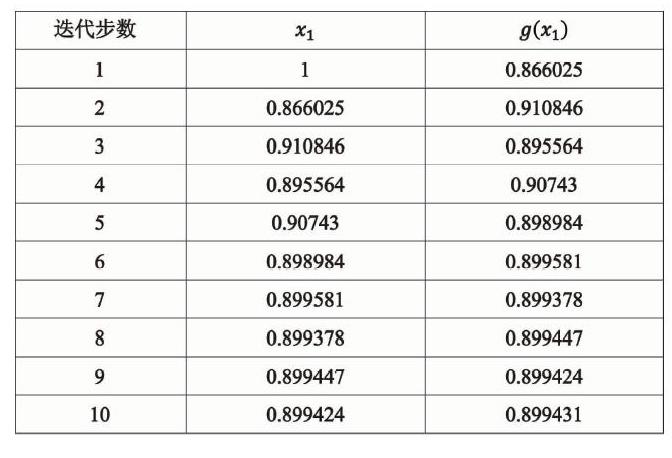
我们将迭代使用的近似根列在下表中：

这样，经过三步迭代之后，我们得到该方程的一个近似根在0.89附近。并且10次之迭代后，我们可以确定该方程的一个根的前四位有效数字为0.8994。

（三）不动点法局限性

仍以方程x4+x3+2x2-3=0为例。若构造函数                      。

然后以同样的思路，我们发现经过几次迭代后并不收敛。所以不动点法求根，具有一定的局限性。

四、结语

三种方法都是求解近似根的方法。首先都需要确定一个初始迭代值，然后逐步迭代，逼近方程的理论上的实数根。并且都只是求解出一个或者几个近似根，并不能在理论上保证求出所有的根。

二分法易于理解，并且使用范围广。只要在连续函数区间[a，b]上由                    ，就能夠通过二分法求得该方程的一个解。但是，其收敛很慢，需要迭代步数多。最终确定的是根的所在小区间，而且无法判断所求根更靠近区间的哪一端。

牛顿法也易于理解。相较于二分法，它的收敛很快，但是适用范围小，对有的方程迭代后并不收敛，需要重新选取初始迭代值，或者选用别的方法。所以牛顿法具有一定的局限性。

不动点法原理不是很易于理解。相较于二分法，它可以较快地收敛。相较于牛顿法，它的步骤简单。但是，不动点法使用范围小，对于一些方程迭代后并不收敛。所以不动点法也有一定的局限性。

所以，在求解实际问题中，选取何种方法，要由方程本身的性质决定，也要考虑收敛速度的因素。尽量选取既适用，又可以迅速得出近似根的方法。

参考文献：

[1]陆桂菊.求方程的近似解与近年高考题[J].数学通报，2013，（02）：47-50+53.

[2]王涵，匡佳佳，许国会.“用二分法求方程的近似解”一课教学设计[J].高中数学教与学，2018，（10）：16-18.

[3]卢钦和.方程近似解、二分法及其它（续）[J].中学数学月刊，2005，（10）：1-3.

[4]张晓勇，王仲君.二分法和牛顿迭代法求解非线性方程的比较及应用[J].教育教学论坛，2013，（25）：139.

[5]张丽娅.不动点原理在分析中的应用[J].甘肃联合大学学报（自然科学版），2007，（04）：25-26+35.

（作者单位：河北石家庄精英中学）