一种基于拉-剪破坏的边坡动力稳定性分析方法
彭雪峰,朱亚林,2,马 驰,檀 昆
(1.合肥工业大学 土木与水利工程学院,合肥 230009; 2.土木工程结构与材料安徽省重点实验室,合肥 230009)
在工程中,边坡稳定性分析是伴随着土压力和地基承载力理论一起发展起来的[1-4].库伦和朗肯建立了一系列关于土压力的计算方法,学者们将其运用在边坡稳定分析方面并形成了体系,即极限平衡法[5].极限平衡法的基本特性是:在摩尔-库伦破坏准则基础上建立静力平衡条件,针对土体破坏时力的平衡状态来求问题的解[6].然而,在实际中,很多情况是静不定状态.为了使原本静不定问题变成一个静力问题,极限平衡法会引入一些简化:设定滑裂面形状为折线、圆弧、对数螺旋线等;放松静力平衡要求,求解过程中仅满足部分力和力矩的平衡要求;对多余未知数的数值或分布形状作假定[7-8].但由于该方法没有考虑到土体的本构性质,不能求出失稳时土体各处应力和应变,无法反映土坡的破坏机理.所以,采用这种方法求出的仅仅是一种综合性近似解答.
从进入20世纪70年代之后,随着有限元理论方法的完善和计算机水平的提高,使用严格的应力应变分析结构成为可能[9].一般来说,数值分析都是和强度折减法一起使用.强度折减法对边坡上的强度指标(摩擦系数φ和黏聚力c)进行折减,并且通过以力和位移作为收敛标准得到一个新的强度指标,再与原先的强度指标做比值即为安全系数[10].从强度折减法的基本概念出发,对于同一个边坡,理论上只有一个折减后的强度指标.于是,当进行动力分析时,会导致无法直接通过折减强度得到不同时间步上的安全系数.
为了能够了解边坡在地震中抵抗滑动破环的能力.文献[11]利用矢量和法计算得到边坡安全系数时程图.矢量和法是基于边坡真实应力状态,将已知滑动面上的滑动矢量和抗滑矢量在相同下滑方向作投影并求和,两者的比值为安全系数[12].以往学者在利用矢量和法进行边坡稳定性分析时,往往只是将边坡滑动面处理成剪切破坏.但是,由文献[13]论述:在地震作用过程中,边坡主要破坏形式是由坡顶向下一定深度内的拉破坏和坡脚向上延展的剪切破坏共同组成贯通破裂面.为了更加符合在地震作用下边坡的破坏模式,本文结合拉-剪破坏强度准则对矢量和法进行优化,使得到的安全系数时程图更能反映边坡真实抗震性能.
1 基于拉-剪破坏的矢量和方法
1.1 考虑抗拉强度矢量和方法安全系数公式推导
1.1.1 矢量和法的讨论
矢量和法的优势是基于边坡真实应力状态,而与之相对应的安全系数称为矢量和法安全系数,其具体定义:在边坡潜在滑动面上,极限抗滑力矢量在整体下滑趋势方向上投影代数和R与总下滑力矢量在相同方向上投影代数和T的比值[14].受力分析如图1所示,边坡计算区域内潜在滑动面S已知,σs、σn、στ为滑动面A点的应力矢量、法应力矢量和剪应力矢量,σ′s、σ′n、σ′τ为滑动面B点的极限抗滑应力矢量、法应力矢量和剪应力矢量,m为潜在滑动体的整体下滑趋势方向.滑动面上各点的应力矢量和极限抗滑应力矢量在m上投影求和,并做比值就得到相应的安全系数.
具体公式如下:
(1)
式中,分母是边坡真实应力矢量和在整体下滑趋势方向做投影.分子代表一个边坡在滑动面S上极限抗滑能力,如何量化边坡极限抗滑能力是讨论重点.
先对“σ′n+σ′τ”进行分析,极限抗滑能力是由极限抗滑法应力矢量σ′n和剪应力矢量σ′τ共同提供.在矢量和法中,极限法应力矢量σ′n的大小等于该点岩土法应力矢量σn,方向与之相反;而极限剪应力矢量σ′τ的大小满足Mohr-Coulomb强度准则(τ=σntanφ+c),方向为该点在滑动面上剪应力的反方向.接着,对于整体下滑趋势方向m而言,有3种计算方法:a)利用从潜在滑动面剪入点到剪出点的连线作为下滑方向;b)潜在滑动面剪应力矢量和的方向;c)潜在滑动面极限抗剪应力矢量和的反方向[15].假设:当滑动体产生实际的位移时,定义此时的滑动方向为整体下滑趋势方向m.为了满足这种情况需要将抗滑应力达到最大值(极限抗滑强度),所以,本文选择方法c).

图1 沿潜在滑动面受力分析图
从上文中可以看出,无论是对于极限抗下滑应力矢量σ′s还是整体下滑趋势方向m,对边坡潜在滑动面上的抗滑强度准则选取都有重要的作用.在静力学边坡稳定分析中,潜在滑动面主要是受剪破坏[16].但经过调查发现,边坡在地震的作用下,坡顶区域会发生拉裂破坏,有些岩石甚至被抛出[13].如果仅仅认为在滑动面上极限抗滑强度全部来源于抗剪强度,无疑会造成一定的误差.基于以上关于矢量和法的思考,下面将给出考虑抗拉强度的矢量和法的推导过程和计算方法.
1.1.2 拉-剪破坏下矢量和法安全系数
首先,利用数值分析手段得到边坡应力场和潜在滑动面,对滑动面所在单元进行应力矢量计算.任取一个单元P,由弹性力学基本公式可得
(2)
式中:σi表示潜在滑动面上一点应力张量,σm、σn、στ分别表示在该点应力矢量,法应力矢量和剪应力矢量,n表示该点平面的单位法向量.
1.1.2.1 矢量和安全系数公式推导
基于矢量和法安全系数关键是求出下滑面极限抗滑能力.动荷载作用使得边坡上部形成拉裂缝.如图2所示,设滑动面区域中包含受剪区域有pi个单元,受拉区域有pu个单元.H1到H2为受剪区,按照1.1.1节所述方法计算滑裂面极限抗滑强度,其滑裂面上的极限抗滑矢量σ′mi、法向应力矢量σ′ni、剪应力矢量σ′τi满足如下公式:
(3)
式中:φ、c分别为岩土内摩擦角和黏聚力.

图2 边坡极限抗滑能力受力示意
H2到H3为受拉区,其极限抗滑应力矢量σ′mu中的法向应力矢量σ′nu大小由岩土抗拉强度确定,极限抗剪应力矢量σ′τu大小等于该点剪应力矢量,公式如下:
(4)
式中ftu为岩土抗拉强度.
将极限抗滑应力矢量在整体下滑趋势方向反方向做投影,并求和可得
(5)
由式(3)、(4)、(5)可得
(6)
对于总下滑力,由边坡潜在滑动面上应力在整体下滑趋势方向上求解代数和可得
(7)
(8)
1.1.2.2 整体下滑趋势方向确定
为了将两个矢量和能够在相同方向进行投影并做比较,需要判断出滑动体在滑动面上可能的下滑趋势方向.为了满足“相对运动趋势与静摩擦力相反”的基本物理意义,当已知边坡坡顶处是受拉破坏,原先下滑方向公式需要做相应的调整.其中,对于受剪滑动面上,滑动体是沿着滑动平面的切线方向运动,所以,利用极限抗剪强度σ′τi作为计算整体下滑方向因子;对于受拉滑动面,由于边坡潜在滑动体是背离边坡方向运动,利用滑动面上极限受拉强度σ′nu作为计算下滑方向因子,即可以得
(9)
将式(3)、(4)代入式(9)可得
(10)
1.2 滑动面计算
一般边坡滑动失稳是沿着剪应变增量最大部位发生,所以,通过剪应变增量去确定剪切破坏面位置,再利用地震作用下所得受拉破坏区域来判断受拉滑动面高度,两者共同形成贯通复合滑动面[17].本文利用FLAC程序计算的边坡应力场,其应力信息是存储在单元格中.首先,利用剪切应变增量云图确定滑动面大致范围(见图3),自定义单位层高h,从坡脚H1进行逐层搜索直到坡顶H3并得到每层剪切应变增量最大值点;接着,根据单元应力状态找出受拉屈服单元,将这些单元所在区域最大竖直高度作为拉裂缝深度H2;最后,从H1到H3将所有最大值点通过n阶多项式(如式(11))进行拟合可以得到剪切破坏模式下的滑动面曲线l1,若利用H1到H2高度范围内最大值点进行拟合并结合受拉裂缝竖直线段(H2~H3)便可得到拉-剪破坏模式下的滑动面曲线l2.这里有两点需要说明:1)剪切应变增量最大值的坐标是所在单元中心坐标,可能会出现拟合之后曲线所对应坐标偏移离开原先的单元中心坐标,这时需要进行调整;2)由于FLAC软件中应力状态都储存在单元中,受拉裂缝深度的精度取决于网格划分的尺寸,单元划分越小精度越高.在实际中,岩土颗粒小于网格尺寸,所以,本文采用方法得到的受拉裂缝深度会稍大于实际的拉裂缝深度,提供一定冗余度.
拟合多项式表达式:
(11)
式中ai为待求系数.
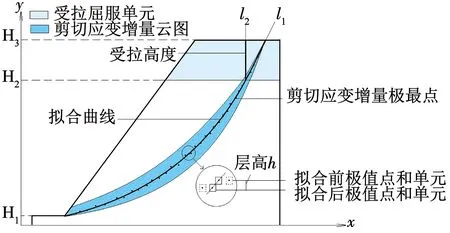
图3 滑动面搜索方法示意
1.3 地震作用下边坡稳定性分析过程
采用数值分析程序FLAC可以精准模拟地震波在土体中传播并且得到各个单元应力.首先,根据边坡物理、几何参数建立相应模型,在输入地震荷载之后进行动力求解.然后,提取每个时刻各个单元上应力大小、方向、剪切应变增量以及单元状态.再使用MATLAB自编程序得到滑动面单元上应力信息,最后,利用1.1中优化后的矢量和方法求解得到每个时刻的安全系数并对边坡的稳定性进行评价分析,具体流程见图4.
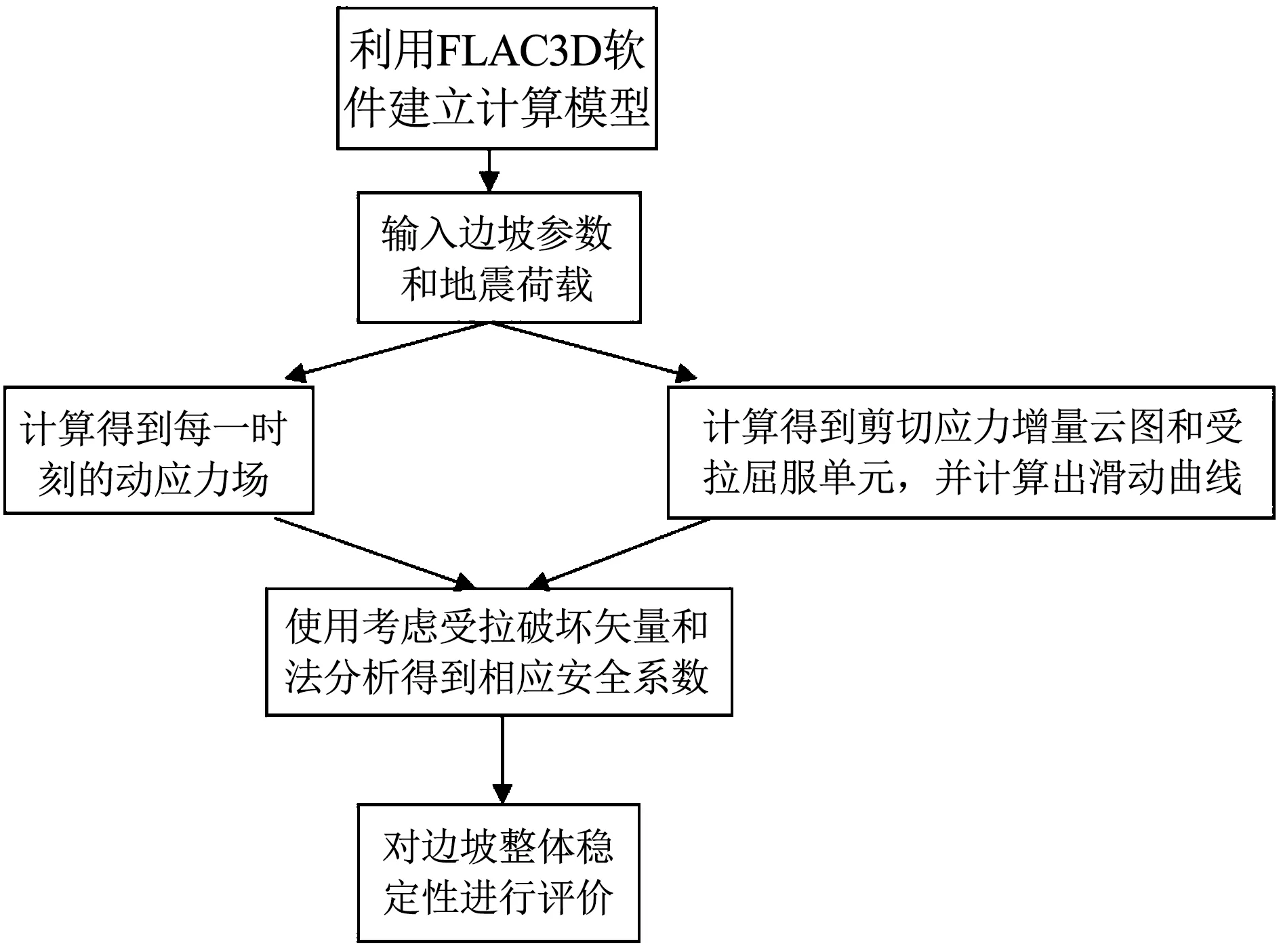
图4 边坡稳定性分析流程
1.4 算法验证
为了验证本文得到的边坡安全系数算法合理性,利用强度折减法与本文新方法进行对比分析边坡动稳定性.由于强度折减法局限性,采用拟静力法计算地震作用效应,水平地震惯性力代表值按照相应规范标准公式,设计烈度为7度,水平向设计地震加速度代表值为0.98[18].边坡岩土采用Mohr-Coulomb准则,详细参数:坡高H=5 m,坡比i为1∶1.50,黏聚力c=50 kPa,内摩擦角φ=30°,剪切模量G=10 GPa,体积模量K=30 GPa,抗拉强度T=5 kPa.
图5为模型单元状态分布图.可以看出,边坡腹部单元主要受到剪切破坏,坡顶出现了受拉破坏单元,这与文献[13]分析的结果相吻合,表明在动荷载中坡顶破坏形式主要是由拉裂缝组成.

图5 边坡单元状态图
将边坡单元剪切应变增量数值提取出来,以自定义层高为基本单位进行逐层搜索,将搜索得到最大值点利用式(11)拟合成多项式函数,为了防止曲线的上凸,选用多项式的最高次数n为3,具体系数见表1.

表1 多项式系数
图6为两种不同破坏模式下拟合曲线.其中,剪切破坏模式下的滑裂面曲线拟合高度范围为从坡脚一直到坡顶,即竖向范围:h1=0.2 m~h3=5 m;对于拉-剪破坏模式下的滑裂面曲线拟合从坡脚到受拉裂缝深度处,即竖向范围为h1=0.2 m~h2=4.3 m,剩余部分按照受拉竖直裂缝处理,即范围为h2=4.3 m~h3=5 m.
由拟合曲线逐层提取相应单元应力场,并带入公式可以得到下滑趋势角度和矢量和法安全系数,再利用FLAC自带的强度折减法计算安全系数作为参考对比,具体数据见表2.可以看出,本文改进后拉-剪破坏矢量和法的安全系数和强度折减法只差了0.01,表明了本文方法的正确性,而剪切破坏的安全系数相对来说,比另外两种方法数值偏大.

图6 拟合曲线示意
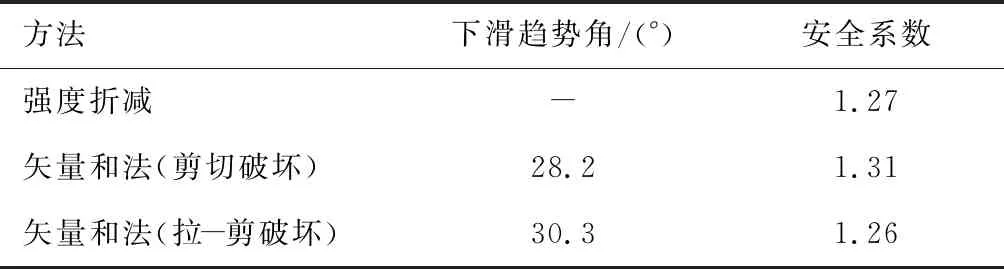
表2 边坡安全系数与下滑趋势角
2 算例分析
2.1 边坡模型概况
边坡模型为某一岩质边坡,边坡高度为41 m,边坡按照1∶1.00放坡,详见图7.为了满足精度要求,模型左边界离坡脚距离20 m,坡顶到右边界距离为35 m,下边界到坡脚的距离为20 m.

图7 边坡二维计算模型
岩土材料采用Mohr-Coulomb强度准则,第1岩土层(1#)为全风化花岗片麻岩,第2岩土层(2#)为强风化花岗片麻岩,具体材料参数如表3所示.其中模型四周设有自由边界场,阻尼采用瑞利阻尼,其中通过计算得到阻尼比为0.05,最小中心频率为4.065 Hz,计算过程参见文献[19-20].

表3 土体力学参数
通过对某地区100年超越频率为2%的基岩期望反应谱曲线进行拟合而得到人工波(如图8),其加速度峰值为0.28g.在计算过程中,在模型底部以水平方向输入加速度峰值为0.28g,竖直方向输入加速度峰值为水平方向的2/3,地震总共历时20 s.

图8 输入地震时程曲线
2.2 边坡滑动界面分析
图9为边坡在不同地震时刻单元状态图.可以看出,当t=1 s时,单元状态主要是在坡脚处出现剪切破坏单元并且向坡内方向延伸,只有在坡顶处出现个别的拉破坏单元.当t=2.2 s时,地震波震荡明显加剧,坡顶拉破坏单元不断扩大并且与剪切破坏单元连同形成贯通界面.在图9(c)中,t=6 s时地震波达到峰值,边坡的腹部大部分已经发生了剪切破坏,并且坡顶的拉破坏区域明显增加.图9(d)为地震t=12 s时刻的单元状态图,整个边坡大部分单元都发生过了剪切破坏,坡顶区域也从地震最开始的2.2 s出现的个别拉破坏单元一直到地震持续时间末端被拉破坏单元的完全覆盖.
通过前文对边坡单元状态的分析,可以根据拉破坏单元得到受拉裂缝深度.利用受拉裂缝深度选取受拉区域高度,结合相应的单元剪切应变增量最大值点可以分别拟合出两种破坏模式下的潜在滑动面曲线,拟合多项式最高次数为3次.由于篇幅问题,仅仅展示了1,5,10,15,20 s的拟合曲线系数,见表4,5.

表4 拟合曲线系数(剪切破坏)

表5 拟合曲线系数(拉-剪破坏)

图9 边坡单元状态动态图
图10,11为5个时间节点两种破坏模式下的边坡滑动面拟合曲线.通过对小部分曲线群放大可以看出,随着时间的推移,地震滑弧有一定的变化.这是由于地震持续过程中,滑动体的位移是一个逐渐增大的过程,使得剪切应力增量整体向坡内平移,进而求得的拟合曲线也有向坡内走移的趋势.

图10 剪切破环拟合曲线示意

图11 拉-剪破坏拟合曲线示意
根据不同的拟合曲线,分别提取相应单元并求出边坡下滑趋势角度(如图12).可以很容易看出,整体上根据拉-剪滑裂面求出的下滑矢量角要大于剪切滑裂面的下滑矢量角;在地震过程中,最大差值达4.5°,出现在19.7 s时刻;最小差值为0.13°.这是由于坡顶拉裂缝的出现改变了原先滑动面的轨迹使得下滑角度增大,不利于边坡稳定性.

图12 边坡整体下滑趋势角度时程
2.3 边坡稳定安全系数时程分析
图13,14分别为剪切破坏和拉-剪破坏的滑动合力和抗滑合力.从整体趋势看,两种不同方法的合力变化趋势和地震波波动趋势一致,在4~6 s、和8~10 s波动最大;在数值上,拉-剪破坏下滑动合力和抗滑合力相较剪切破坏都要偏小.一方面是由于投影矢量角度变大,另一方面是由于在拉裂破坏面引入了抗拉强度条件.

图13 边坡的动态响应规律(剪切破坏)
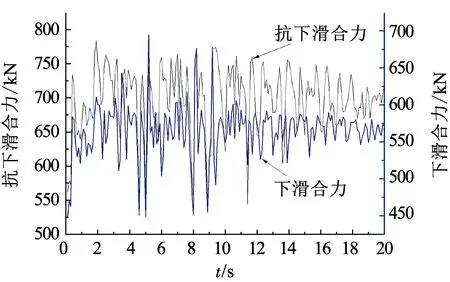
图14 边坡的动态响应规律(拉-剪破坏)
利用两种不同的方法分别对边坡的安全系数进行计算,图15为两种方法的安全系数时程图.整体上看出,两种方法所得到安全系数趋势一致,表明新方法在时程分析上的可靠性;其中拉-剪破坏的安全系数大小波动范围为1.047~1.574,剪切破坏的安全系数大小波动范围为1.077~1.622,前者比后者小了2.8%~3%.比较两者大小可以得到,增加了拉裂面的安全系数比原先方法得到安全系数要小,表明以往用矢量和方法进行边坡动稳定性分析时,会高估边坡的抗震性能,不利于边坡的抗震设计.

图15 边坡安全系数时程图
当地震时间为11.4 s时,两种方法所得安全系数为最小值,拉-剪破坏的安全系数为1.05,剪切破坏的安全系数为1.07;当地震时间为9.4 s时,所得安全系数为最大值,其中前者为1.57,后者为1.62.图16为t=11.4和9.4 s时刻边坡的加速度矢量图.在地震时间为11.4 s时刻,边坡的加速度矢量均朝向边坡外侧,这是对边坡动稳定性最不利的状态,观察地震波加速方向,在下一秒加速度方向出现了明显的改变,安全系数得到一定的增加,所以,此时计算得到的安全系数最小,是边坡最不利的状态.同样,当t=9.4 s时,加速度矢量的方向大致是朝向边坡内部,这种状态有利于边坡的稳定性,并且在下一秒地震波的加速度发生了改变,安全系数又得以恢复,所以,t=9.4 s时计算的安全系数达到最大值.
2.4 边坡动力稳定性综合评价
一般来说,边坡动力稳定性评价的具体指标在国内外还没有形成统一的标准,其中比较主流两种指标为永久位移和安全系数.当前,基于安全系数时程图进行边坡稳定性评价方法大体分为平均安全系数[21]、最小动安全系数[22]和基于可靠度理论的动力安全系数[21].平均安全系数是指利用安全系数时程图各个点的平均安全系数作为评价的指标;最小动安全系数就是以安全系数时程图中的最小安全系数作为评价的指标;而基于可靠度理论的动力安全系数Kf的表达式如下:
(12)
式中:N为安全系数时程的时间点总数,K(ti)为ti时间点上对应的安全系数,β为边坡失效概率的可靠度指标.
本文将失效概率设置为1%,在其失效概率情况下对应的可靠性指数为β=2.33,再结合各个时间节点的安全系数带入式(12)后得到相应的边坡动力安全系数,并将得到结果编制成表6.可以清晰看出,3种对边坡动力稳定性评价指标均大于1,说明在当前地震荷载情况下,边坡处于安全范围内不会发生失稳破坏;对比拉-剪破坏的安全系数和剪切破坏的安全系数,所有指标均是前者较小,其中动力安全系数前者为1.07,后者为1.11,两者相差3%.

表6 边坡整体动安全系数计算结果
3 结 论
1)通过算例将强度折减法、剪切破坏矢量和法和拉-剪破坏矢量和法3种方法对比分析,结果表明,在动荷载情况下拉-剪破坏矢量和法得到安全系数更加精确.
2)在地震作用下,边坡潜在滑动面会发生变化,并且随着地震持续时间增加,滑动面向着边坡内侧走移.
3)拉-剪破坏模式下边坡整体下滑趋势角度相对剪切破坏的矢量角度有所增大,表明坡顶的拉裂缝改变了原先的下滑趋势角度.
4)拉-剪破坏的安全系数要低于剪切破坏的安全系数,说明原先的矢量和方法高估在动荷载作用下边坡的抗震性能,这会不利于边坡的抗震设计.

