基于离心机法获取定体积质量下的土壤水分特征曲线

任健，张吴平，王国芳，黄明镜，乔磊

基于离心机法获取定体积质量下的土壤水分特征曲线

任健1，张吴平2*，王国芳1，黄明镜3，乔磊1

（1.山西农业大学 资源环境学院，山西 太谷 030800；2.山西农业大学 软件学院，山西 太谷 030800；3.山西省农业科学研究院 旱地农业研究中心，太原 030000）

【】克服离心机法测定土壤水分特征曲线时“变体积”的缺陷，实现用离心机法获取扰动土壤准确的土壤水分特征曲线。选取了山西省16种粒径组成、有机质量差别显著的扰动土壤作为研究对象，采用离心机法测定了初始体积相同的各土壤样品在不同转速下的土壤体积含水率、动态变化的土壤体积；采用多元非线性回归模型，描述了以土壤体积含水率、粒径组成、体积质量和有机质质量分数作为自变量描述土壤水吸力的函数关系，并对模型进行了验证与评价。土壤水吸力的自然对数函数可以表示为土壤砂粒质量分数、黏粒质量分数、土壤体积质量和含水率乘积以及有机质质量分数等土壤属性的线性函数，模型的决定系数达到0.740；模型建模样本平均相对误差为14.460%，验证样本平均相对误差为13.237%，模型预测精度较高；同时发现土壤属性对于曲线的形状与走势的影响不能忽视，其中砂粒质量分数、土壤体积质量和含水率乘积与土壤水吸力负相关，黏粒质量分数、有机质质量分数与土壤水吸力正相关。因此，本方法构建的模型更符合实际情况，能够提高土壤水力学参数的精度，同时可以克服离心机测量土壤水分特征曲线体积变化的缺点，得到更合理的土壤水吸力和土壤含水率的关系。

土壤水分特征曲线；多元非线性预测模型；离心机法；仿真数值模拟

0 引 言

土壤水分特征曲线是土壤含水率与土壤水吸力的函数，反映了土壤数量与能量之间的关系，是获取土壤非饱和导水率、定量模拟土壤水分溶质运移及科学灌溉的重要参数，在科学研究和生产实践中有重要意义[1-5]。

目前对于土壤水分特征曲线的测定包括间接推求法和直接测定法，一些研究通过土壤颗粒分布曲线、土壤体积质量、质地、田间持水率和萎蔫含水率等土壤属性来间接地推求土壤水分特征曲线[6-9]。虽然间接推求法成本较低，但是其精度不高，在生产实践当中难以推广[10]。

当前对于农田尺度的研究更多的是采用直接测定法，常用的方法有张力计法、离心机法、压力膜仪法等。其中，离心机法操作较简便，测得的吸力范围较广，省时省力，土壤中的水分更易排出[11]。但是土样在离心的过程中，体积会越来越小，因此采用该方法获取的土壤水分特征曲线是在“变体积”情况下测得的。吕殿青等[12]发现武功粉砂质黏土在用离心机测定土壤水分特征曲线时，体积质量在1.02～100.2 m水柱范围内从1.398 g/cm3增加到了1.858 g/cm3，变幅达到了0.565 g/cm3；聂坤堃等[11]发现用离心机法获取土壤收缩特性时，扰动土样初始设计体积质量分别为1.30、1.35、1.40 g/cm3的情况下，体积质量变幅分别达到了37.69%、33.33%、28.57%。邵明安[13]认为土壤持水性质不是一条单一的曲线，而是由土壤含水率、体积质量、吸力共同组成的一个空间曲面，可见体积质量对于土壤水分特征曲线的影响不能够被忽视。

为了克服离心机“变体积”的缺陷，吕殿青[14]采用了“石蜡法”获取了定体积质量下的土壤水分特征曲线，通过设定不同离心机转速使土样达到不同转速下的平衡状态，并在平衡状态的土样中注入了熔化的石蜡，待石蜡冷凝后会使土壤体积固定，从而得到定体积质量下的土壤水分特征曲线，但此方法只能测定土样平衡状态下该体积质量下的定体积质量曲线，如果要测定不同体积质量梯度下的曲线还需多次设定离心机转速来获得不同平衡状态、不同初始体积质量的土样，并且体积质量不易控制，因此“石蜡法”有自身的局限性，操作起来较为不便。

除此之外，离心机法获取的土壤含水率范围有限。由于离心机转子的转速有限，因此不能够获取在极低含水率下的土壤水吸力值。同时，相关研究指出，土壤水分特征曲线除了受到体积质量变化的影响外，还受到土壤粒径组成、有机质质量分数的影响[15-16]。已有研究表明土壤质地、有机质质量分数对土壤水分特征曲线的影响极大，且与Van Genuchten模型当中的参数相关性极高[15,17]。

基于此，本研究拟采用离心机法直接获取不同粒径组成、有机质质量分数土壤的“变体积”下的土壤水吸力和含水率。根据实测结果，采用统计回归分析模型，构建以土壤水吸力对数为因变量，土壤体积质量、含水率、粒径组成、有机质及各因素变量的两两乘积作为自变量，建立土壤水分特征曲线多元非线性预测模型；采用仿真数值分析方法克服“石蜡法”所带来的缺陷，排除体积质量对其曲线的影响，克服离心机法的缺陷，并同时考虑粒径组成和有机质对土壤水分特征曲线的定量影响，其建模结果可以自由设定土壤体积质量的值，从而最终获取“定体积质量”下的土壤水分特征曲线，并对所建预测模型进行验证与评价分析。以作为黄土高原区开展的旱作农业中土壤水分运动的定量模拟和预测，调节土壤水分有效性及储水量，对指导旱作农业的灌溉与排水具有重要意义。

1 材料与方法

1.1 供试土壤

此次研究选择山西省16种不同质地、有机质质量分数的土样。在每个采样区选取代表性的地块将部分扰动土用塑封袋带回。将采集到的扰动土样带入室内自然风干，研磨过2 mm筛，作为此次离心机当中的供试土样，并按照初始体积质量为1.3 g/cm3均匀装入直径为5 cm、高度为3 cm的环刀中。采用烘干法测定土样残余含水率。根据残余含水率的数值可得到土样中干土的质量。将装有扰动土的环刀浸泡于蒸馏水中24 h，水面高度低于环刀高度1 mm，之后将环刀滞空放置一段时间，直到不再有重力水排出，此时认为土样达到饱和，并用高精度电子天平称质量计算获取土样饱和含水率。土壤质地的测定采用比重计法，并按照国际制土壤质地分类为分级标准。土壤有机质质量分数的测定采用浓硫酸-重铬酸钾外加热法。

对山西省土壤16种基本性质的测定，如表1所示，所选的土壤质地与有机质质量分数差异变化较大，砂粒的变化范围是5%～60%，黏粒变化范围是10%～60%，有机质质量分数变化范围是0.248%～2.475%，此变化范围可以代表山西省土壤质地、有机质质量分数的变化，从而大大减少工作量，并且仍能得到试验对象主要特征的试验结果。

1.2 土壤水分特征曲线的获取

土壤水分特征曲线的获取采用离心机法。离心机采用日立CR22N型高速恒温冷冻离心机，并附有土壤水分特征曲线定制转子、土样盒、环刀与排水装置。定制转子最高转速可达11 000 rpm，最大能够同时装填4个离心盒，并具有转头自动识别与转头自锁功能，保证在离心过程中土样盒保持相对静止。试验通过设置离心机不同的转速梯度从而计算得到不同转速下对应的土壤水吸力，为了保证试验的精度，各研究区每层土壤均设置3次重复，每次设置9个不同转速，分别为300、600、1 000、1 600、2 500、3 000、3 500、6 500、11 000 rpm，对应9个不同土壤水吸力。待每个转速下土样平衡之后，取出离心盒，静置一段时间后用高精度电子天平称量土样质量[18]，用游标卡尺测量土样高度，从而计算土样平衡时的质量与体积。根据计算出的土壤体积含水率和所对应的土壤水吸力，即可绘制出土壤水分特征曲线[19]。

1.3 土壤水吸力的计算

邢旭光等[20]在研究土壤水分特征曲线测定过程中土壤收缩特性时，土壤水吸力计算式为：

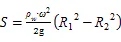
式中：为土壤水吸力（cm）；1为离心机转子轴心至土样中心之间的距离（cm）；2为离心机转子轴心至土样底部的距离（cm）；w为水的密度（g/cm3）；g为重力加速度（cm/s2）；为角速度（rad/s）。

1.4 土壤体积质量的计算

离心机中的土样达到平衡状态之后，根据游标卡尺测得的土样高度可计算体积，根据残余含水率可以计算土样的干土质量，计算式为：

=/[(r+1)π2]，（2）

式中：为土样质量（g）；为体积质量（g/cm3）；r为残余含水率（%）；为环刀内半径（cm）。

1.5 模型精度评估的统计学方法

本次研究结合16种土壤的建模样本数据与另外23组验证样本数据，验证样本数据来自山西省太谷县孟家庄村表层扰动土壤共23个不同转速下的土壤水分特征曲线数据，同建模样本数据的获取方式相同。通过比较模型预测值与实测值的相对误差值、验证样本数据的均方根误差（）、决定系数（2）、误差比的几何平均数（）来分析建模精度[21]：

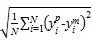
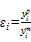
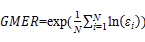
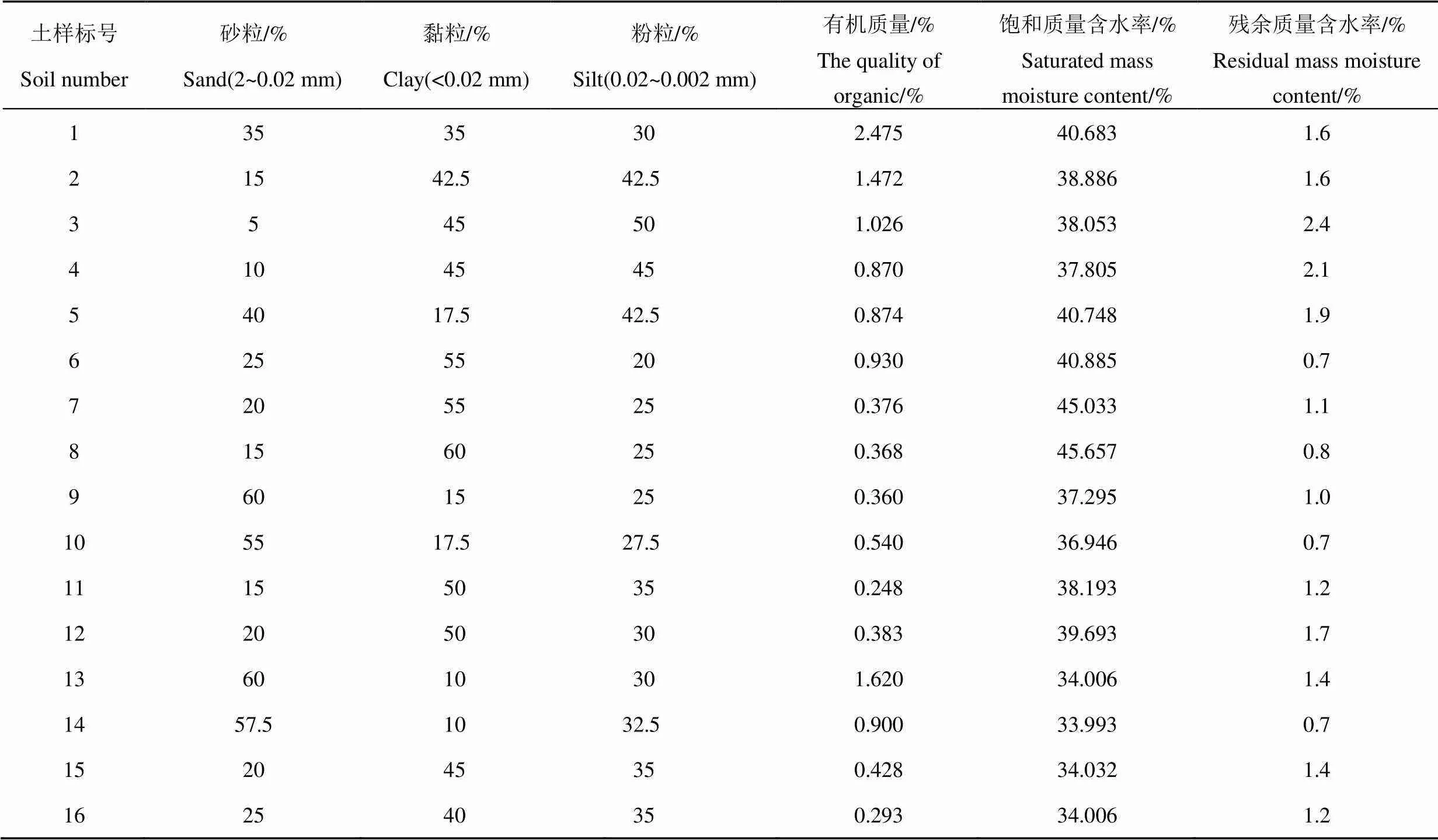
表1 供试土壤基本理化性质

2 结果与分析

2.1 多元非线性预测模型的建立与验证

2.1.1 多元非线性预测模型的建立

多元非线性模型是反映自变量与因变量之间的非线性关系的数学表达式。离心机在获取土壤水分特征曲线时体积质量和含水率在不断变化，将体积质量与含水率的乘积作为自变量，同时将16种供试土壤不同梯度的砂粒质量分数、黏粒质量分数、有机质质量分数作为自变量，通过回归分析预测土壤水吸力，建立如下非线性关系的预测模型：

ln=11.073-0.041+0.057+0.609-14.203，（7）

式中：为土壤砂粒质量分数（%）；为土壤黏粒质量分数（%）；为土壤有机质质量分数（%）；为土壤体积含水率（cm3/cm3）；其余参数同前。该模型决定系数为0.740，相关性较高。

2.1.2 多元非线性预测模型自变量的检验

对建立该预测模型的16组数据进行检验，通过SPSS回归结果进行分析，结果见表2。通过Excel软件中的tinv函数计算得到（0.05，143）的值为1.977。由表2结果得知，4项参数的统计量值的绝对值全部大于1.977，值全部小于0.05，均通过检验，说明具有统计学意义，最终可确定式（7）所建预测模型。

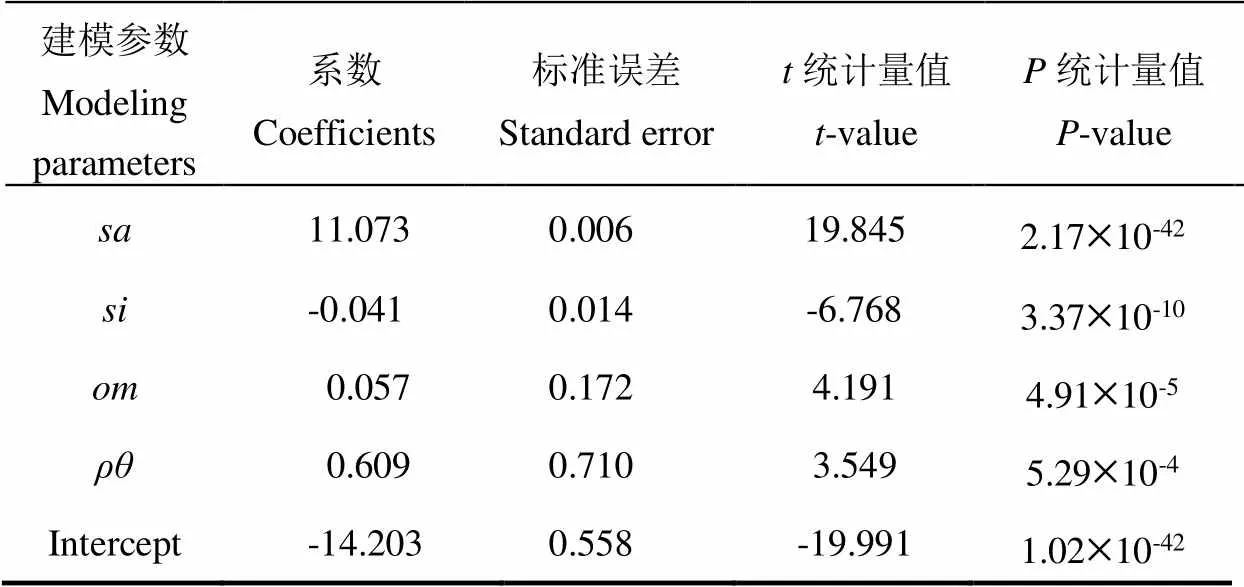
表2 非线性预测模型t值检验表

2.1.3 多元非线性预测模型检验

检验实际为对回归关系的方差分析，对建立该预测模型的16组数据进行显著性检验，通过SPSS软件中的回归统计模块求出值，并比较显著性水平为0.05下的值，结果见表3。

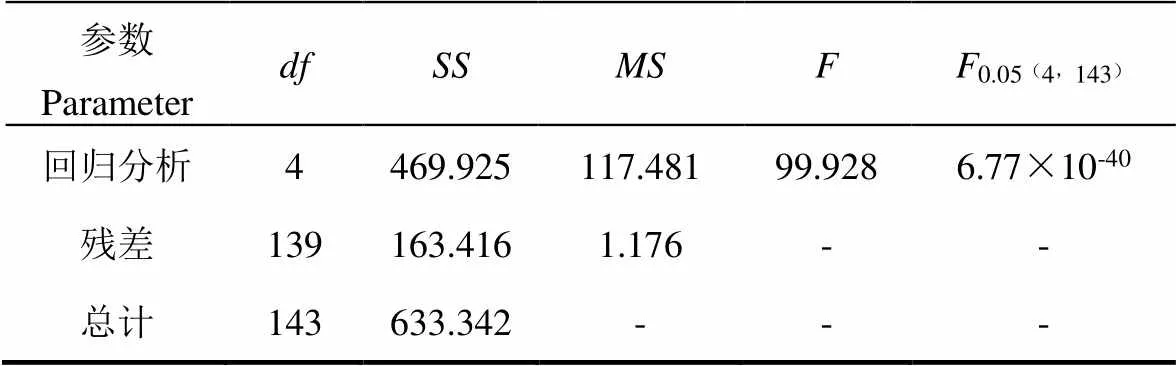
表3 非线性预测模型F值检验表

由表3可知，回归分析建立的非线性预测模型通过了检验，检验统计量值为99.928，大于显著性水平为0.05下的值，表明该模型的土壤水吸力与其余4个自变量具有统计学上极显著的意义，是有效的。

2.1.4 预测模型的验证

上述模型的建立共16条土壤水分特征曲线数据，每条曲线含有9个不同梯度的含水率—吸力数据，总共144个样本数据，做出此144个样本吸力对数的实测值、预测值、相对误差值。由图1可知，建模样本相对误差平均值为14.460%，精度较高，说明用离心机法结合土壤基本属性推求吸力预测模型是可行的。

另外做出23个验证样本吸力对数的实测值、预测值、相对误差值如图2所示。由图2可知，验证样本的平均相对误差平均值为13.237%，其精度与建模样本的精度相当。无论在模型的建立阶段和验证阶段，其相对误差平均值都较低，说明该预报模型精度较高，具有较强的适用性，可以用于土壤水分特征曲线的预测。

将23组验证数据代入预测模型中，对比分析预测吸力对数与实测吸力对数，并根据式（3）—式（6）计算各统计量，结果绘于图3中。由图3可知，预测值与实测值比较接近，基本均匀分布在对称线左右，说明模型预测精度良好；预测值与实测值的决定系数为0.958，说明预测值与实测值的变化趋势基本一致；为1.10，该值大于1，说明预测值较实测值偏大；的值越小，表明预测值与真值的偏差越小，精度更高，其值为0.67，表明预测模型的预测值与实测值吻合度较高。

2.2 根据预测模型模拟各种参数变化下的土壤水分特征曲线

2.2.1 定体积质量下的土壤水分特征曲线的模拟与分析

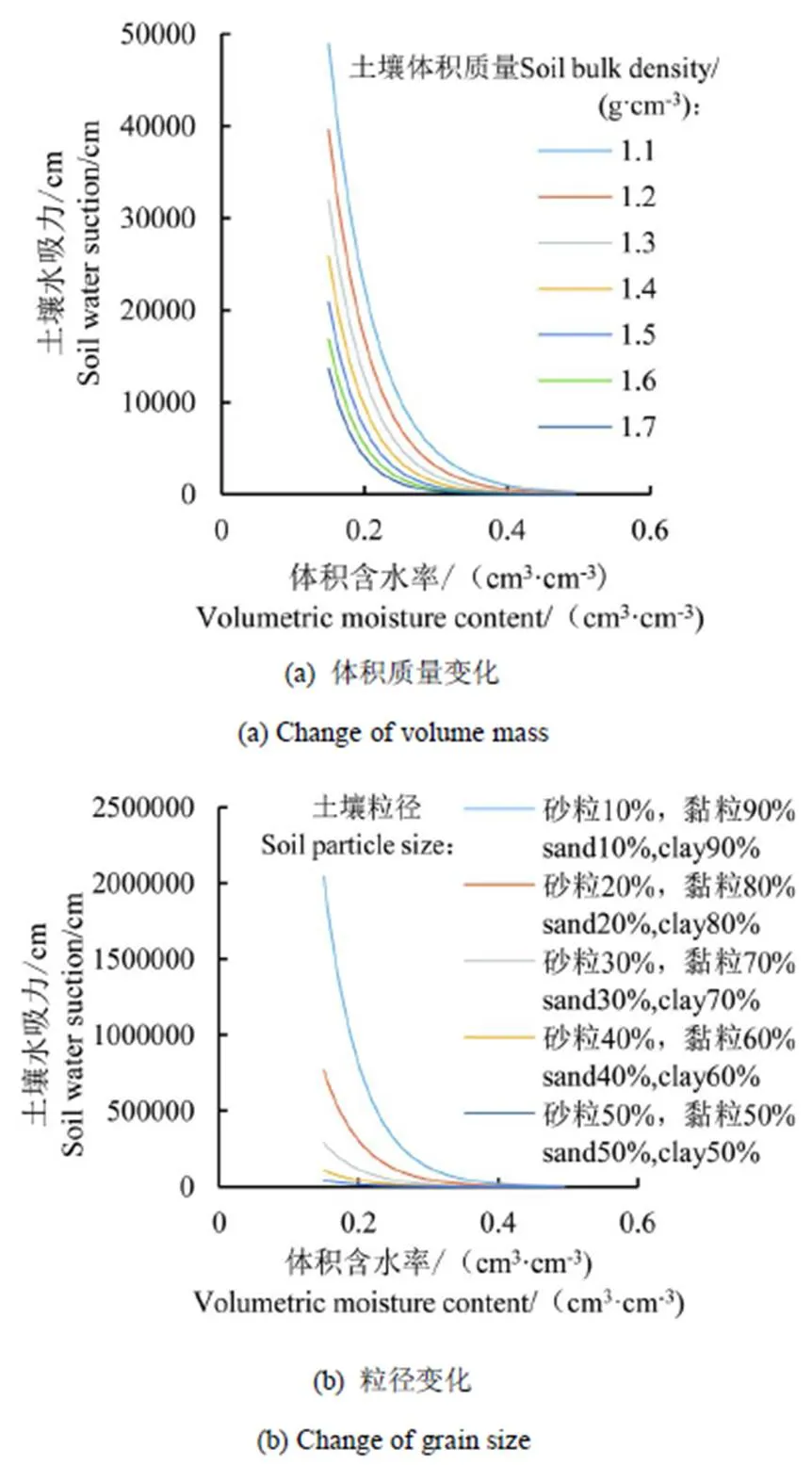
土壤体积质量的变化影响土壤孔隙度[22]，且还会影响土壤孔隙分布，从而改变了土壤的持水特性，势必会影响土壤水分特征曲线。采用仿真数值模拟的方法，将砂粒黏粒配比、有机质质量分数设定为定值，体积质量设定为1.1～1.7 g/cm3，即可获取不同体积质量下土壤水分特征曲线（图4）。由图4可知，随着土壤体积质量的增大，土壤水分特征曲线呈现出向左移动的趋势，且坡度更小；在土壤含水率相同的情况下，高体积质量的土壤表现为更低的土壤水吸力，也就意味着在离心过程中受到较小的离心力的作用即可排出土壤中残留的水分；在相同的吸力下，体积质量较大的土壤所持有的土壤含水率较低。

2.2.2 粒径变化对土壤水分特征曲线的影响分析

土壤质地的差异会改变土壤水分特征曲线的特性，砂粒质量分数高的土壤，其通透性良好，饱和导水率较高，导致土壤对水分的保蓄能力差，在相同的土壤含水率下，砂粒质量分数越高，土壤水吸力越小。在所建预测模型当中，砂粒质量分数的系数为负，即砂粒质量分数与土壤水吸力为负相关。黏粒质量分数高的土壤，土壤的通透性差，饱和导水率较低，土壤对水分的保蓄能力强。由图4可知，在相同的含水率下，土壤水分特征曲线右移，黏粒质量分数越高，土壤水吸力越大，曲线更为陡峭。这验证了预测模型黏粒质量分数与土壤水吸力的正相关关系。

2.2.3 有机质变化对土壤水分特征曲线的影响分析

土壤有机质是土壤固相部分的重要组成，疏松多孔的性质使得能够改善土壤的物理性质，促进微生物和土壤生物的活动，大大提高了土壤储水性质，从而改变土壤水分特征曲线的走势。通过此次仿真数值模拟得知，土壤有机质质量分数越高，土壤水分特征曲线的走势越陡，说明在有机质质量分数高的土壤中，土壤吸附能力更强，这与舒凯民[15]的相关研究结果是一致的。

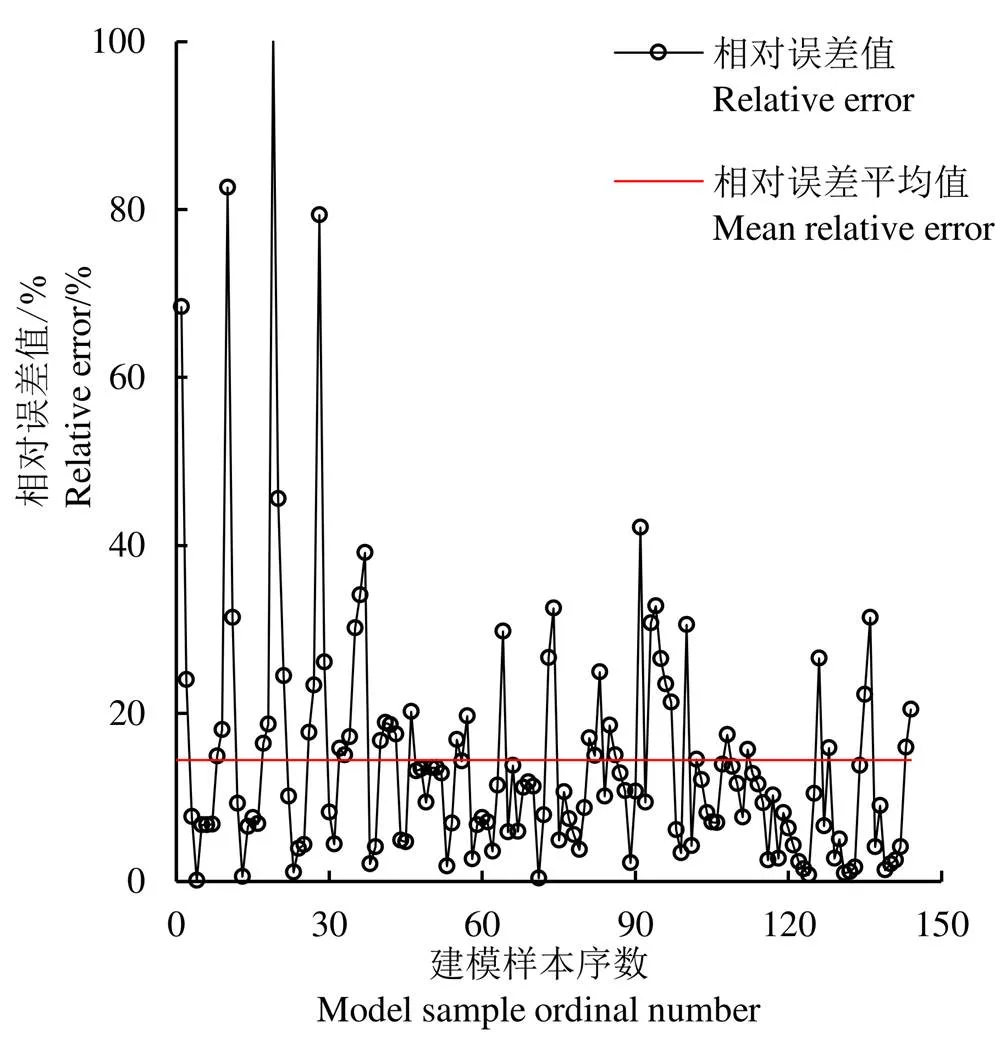
图1 建模样本相对误差图

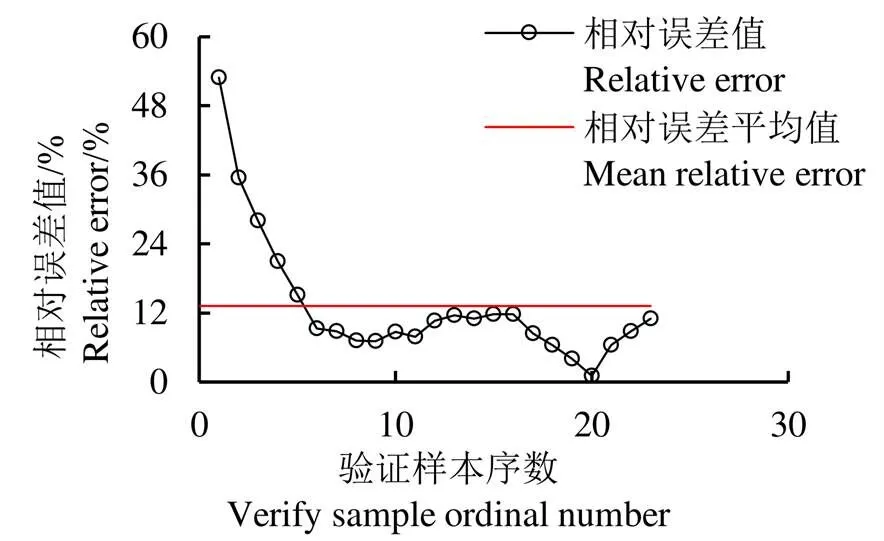
图2 验证样本相对误差图

图3 吸力对数预测值与实测值对比

3 讨 论

通过离心机法直接获取的“变体积质量”下土壤水分特征曲线实测结果，并利用回归分析方法建立其多元非线性预报模型，最后采用仿真数值模拟方法得到“定体积质量”下的土壤水分特征曲线，能够完全实现“石蜡法”的效果[14]，克服了离心过程中“变体积质量”的缺陷。土壤水分特征曲线的多元非线性预测模型相比于Van Genuchten模型而言更加直接。Van Genuchten模型需要众多系数，包括土壤形状系数及进气值系数，这些参数较难获得；而本文提出的模型只需要土壤基本的属性即可推求高精度的土壤水分特征曲线，更方便用于土壤水分运动与农田科学合理灌溉的相关研究。

然而，用离心机法获取土壤水分特征曲线时，由于转子转速有限、极低的土壤含水率对应的土壤水吸力非常大，结果导致缺失土壤含水率极低情况下对应的土壤水吸力数据。在这16种不同的实测土壤水分特征曲线当中，其最大吸力对应的体积含水率最小值为0.083 cm3/cm3，最大值为0.274 cm3/cm3，平均值为0.160 cm3/cm3。对于大田耕作土壤而言，大部分农作物适墒的土壤质量含水率范围在12%~30%之间[2]，换算为体积含水率之后其二者数值相当，可见离心机法所获取的土壤含水率范围与大田耕作土壤含水率基本吻合，缺失的那一段曲线基本可以忽略，因此用离心机法获取土壤水分特征曲线的方法是可行的。

该预报模型建立了土壤多种属性影响下的水分特征曲线，土壤体积质量、质地、有机质质量分数都会显著影响土壤水分特征曲线的形状与走势。多元非线性预报模型的建立表明了通过土壤质地、有机质质量分数、体积质量、含水率即可反映出土壤水吸力，其相关系数为0.740，说明该模型能够预测出74%的土壤水分特征曲线。相比于直接方法获取土壤水分特征曲线，该方法更为便捷。该预测模型可看作土壤水吸力受砂粒质量分数、黏粒质量分数、有机质质量分数、体积质量与含水率的乘积4个因素的决定与影响，各项因素的系数可表达出对模型结果的波动状况，其中体积质量与含水率乘积的系数明显大于其余系数，表明体积质量与含水率的乘积对土壤水吸力的波动之大，更坚定的说明了在用离心机法获取土壤水分特征曲线不能够忽视“变体积质量”对其的影响。

4 结 论

本文所建预测模型相关系数为0.740，通过了检验与检验，建模样本、验证样本的相对误差平均值分别为14.460%、13.237%，值为0.67，所建立的预测模型精度较高；通过仿真数值模拟的方法，得出基于离心机法下获取的定体积质量土壤水分特征曲线，并随着体积质量的减小，曲线有向上移动的趋势；同时也定量表示了预测模型中土壤质地、有机质质量分数变化下的土壤水分特征曲线。

[1] 邵明安, 王全九, 黄明斌. 土壤物理学[M]. 北京: 高等教育出版社, 2006: 67-69.

SHAO Mingan, WANG Quanjiu, HUANG Mingbin. Soil Physics[M]. Beijing: Higher Education Press, 2006: 67-69.

[2] 龚振平, 邵孝侯, 张富仓, 等. 土壤学与农作学[M]. 北京: 中国水利水电出版社, 2009.

GONG Zhenping, SHAO Xiaohou, ZHANG Fucang, et al. Soil science and agronomy[M]. Beijing: China Water Power Press, 2009.

[3] 车政, 王仰仁, 王永红, 等. 农田土壤水分特征曲线参数拟合及其剖面变异特性研究[J]. 灌溉排水学报, 2016, 35(7): 22-27.

CHE Zheng, WANG Yangren, WANG Yonghong, et al. Research on Parameter Fitting of Soil Water Characteristic Curve and Its Variation Property with Depth of Farmland Soil Profile[J]. Journal of Irrigation and Drainage, 2016, 35(7): 22-27.

[4] 于博, 于晓芳, 高聚林, 等. 秸秆全量深翻还田和施加生物炭对不同土壤持水性的影响[J]. 灌溉排水学报, 2018, 37(5): 25-32.

YU Bo, YU Xiaofang, GAO Julin, et al. Change in Hydraulic Properties of Soils Amended with Biochar Following Plough of Straw Stalk into Deep Soil Horizon[J]. Journal of Irrigation and Drainage, 2018, 37(5): 25-32.

[5] 陈安强, 雷宝坤, 胡万里, 等. 洱海近岸菜地包气带土壤水分特征曲线参数变化及其影响因素[J]. 灌溉排水学报, 2018, 37(10): 48-54.

CHEN Anqiang, LEI Baokun, HU Wanli, et al. Water Retention Curve of Vegetative Soils in Erhai Lake Catchment and the Factors Affecting It[J]. Journal of Irrigation and Drainage, 2018,37(10):48-54.

[6] AHUJA L R, NANEY J W, WILLIANMS R D. Estimating soil water retention form simpler properties or limited data[J]. Soil Science Socciety of America Journal, 1985, 49: 1 100-1 105.

[7] MINASNY B, MCBRATNEY A B, BRISTOW K L. Comparison of different approaches to the development of pedotransfer functions for water-retention curves[J]. Geoderma, 1999, 93(3/4): 225-253.

[8] NAVEED M, MOLDRUP P, TULLER M, et al. Prediction of the soil water characteristic from soil particle volume fractions[J]. Soil Science Society of America Journal, 2012, 76(6): 1 946-1 956.

[9] RAJKAI K, KABOS S, VAN Genuchten M T. Estimating the water retention curve from soil properties: Comparison of linear, nonlinear and concomitant variable methods[J]. Soil and Tillage Research, 2004, 79(2): 145-152.

[10] 吕殿青, 邵明安. 非饱和土壤水力参数的模型及确定方法[J]. 应用生态学报, 2004, 15(1): 163-166.

LV Dianqing, SHAO Mingan. Models and determining methods of unsaturated soil hydraulic parameters[J]. Chinese Journal of Applied Ecology, 2004, 15(1): 163-166.

[11] 聂坤堃, 聂卫波, 马孝义. 离心机法测定土壤水分特征曲线中的收缩特性[J]. 排灌机械工程学报, 2018(3): 1-2.

NIE Kunkun, NIE Weibo, MA Xiaoyi. Characteristic of soil shrinkage during soil water characteristic curve measurement by the centrifuge method[J]. Journal of Drainage and Irrigation Mechanical Engineering, 2018(3): 1-2.

[12] 吕殿青, 邵明安, 王全九. 土壤持水特征测定中的容重变化及其确定方法[J]. 水利学报, 2003(3): 110-114.

LV Dianqing, SHAO Mingan, WANG Quanjiu. Application of fuzzy clustering method in designing fuzzy neural exciting controller of generator[J]. Journal of Hydraulic Engineering, 2003(3): 110-114.

[13] 邵明安, 吕殿青, 付晓莉, 等. 土壤持水特征测定中质量含水量、吸力和容重三者间定量关系I. 填装土壤[J]. 土壤学报, 2007, 44(6): 1 003-1 009.

SHAO Mingan, LV Dianqing, FU Xiaoli, et al. Quantitative relationship between mass water content, pressure head and bulk density in determination of soil water retention characteristics i. packed soils[J]. Acta Pedologica Sinica, 2007, 44(6): 1 003-1 009.

[14] 吕殿青, 邵明安, 潘云. 容重变化与土壤水分特征的依赖关系研究[J]. 水土保持学报, 2009, 23(3): 209-212.

LV Dianqing, SHAO Mingan, PAN Yun. Dependent Relationship Between Bulk Density Changes and Soil Water Characteristics[J]. Journal of Soil and Water Conservation, 2009, 23(3): 209-212.

[15] 舒凯民. 基于土壤基本理化参数的土壤水分特征曲线Van-Genuechten模型预报研究[D]. 太原: 太原理工大学, 2017.

SHU Kaiming. Research on Prediction of Soil Water Characteristic Curve Van-Genuechten Model Based on Soil Basic Physical and Chemical Parameters[D]. Taiyuan: Taiyuan University of Technology, 2017.

[16] 杨绪, 赵廷超, 王丰, 等. 基于Gardner模型的黔西南土壤水分特征分析[J]. 灌溉排水学报, 2018, 37(7): 35-42.

YANG Xu, ZHAO Tingchao, WANG Feng, et al. Water Retention Characteristics of Typical Soils in Southwestern Guizhou Province[J]. Journal of Irrigation and Drainage, 2018, 37(7): 35-42.

[17] 舒凯民, 樊贵盛. 基于质地的土壤水分特征曲线参数非线性预测[J]. 人民黄河, 2016, 38(7): 138-141.

SHU Kaiming, FAN Guisheng. The Nonlinear Prediction of Soil Water Characteristic Curve Parameters Based on the Soil Texture[J]. Yellow River, 2016, 38(7): 138-141.

[18] 刘畅, 陈俊英, 蔡耀辉, 等. 斥水土壤水分特征曲线及拟合模型分析[J]. 中国农村水利水电, 2017(7): 45-48.

LIU Chang, CHEN Junying, CAI Yaohui, et al. Soil Water Characteristic Curves of Different Kinds of Repellency Soil and an Analyses of the Fitting Model[J]. China Rural Water and Hydropower, 2017(7): 45-48.

[19] 牛晓彤, 刘目兴, 易军, 等. 三峡山地土壤水分特征曲线及模型拟合[J]. 灌溉排水学报, 2017, 36(9): 75-80.

NIU Xiaotong, LIU Muxing, YI Jun, et al. Water Release Curves and Their Fitting for Soils in the Hills of the Three Gorges Reservoir[J]. Journal of Irrigation and Drainage, 2017, 36(9): 75-80.

[20] 邢旭光, 赵文刚, 马孝义, 等. 土壤水分特征曲线测定过程中土壤收缩特性研究[J]. 水利学报, 2015, 46(10): 1 181-1 188.

XING Xuguang, ZHAO Wengang, MA Xiaoyi, et al. Study on soil shrinkage characteristics during soil water characteristic curve measurement[J]. Journal of Hydraulic Engineering, 2015, 46(10):1 181-1 188.

[21] 姚姣转, 刘廷玺, 王天帅, 等. 科尔沁沙地土壤水分特征曲线传递函数的构建与评估[J]. 农业工程学报, 2014, 30(20): 98-108.

YAO Jiaozhuan, LIU Tingxi, WANG Tianshuai, et al. Development and evaluation of pedo-transfer functions of soil water characteristic curves in Horqin sandy land[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(20): 98-108.

[22] 洪成, 尹殿胜, 陈俊英, 等. 容重对黏壤土土壤水分特征曲线的影响[J]. 节水灌溉, 2018(10): 5-8.

HONG Cheng, YIN Diansheng, CHEN Junying, et al. Impact of Bulk Density on Soil Water Characteristic Curve of Clay Loam[J]. Water Saving Irrigation, 2018(10): 5-8.

Method to Adjust the Soil Water Retention Curve Measured Using Centrifuge Apparatus

REN Jian1, ZHANG Wuping2*, WANG Guofang1, HUANG Mingjing3, QIAO Lei1

(1.Shanxi Agricultural University, College of Resources and Environment, Taigu 030800, China;2.Shanxi Agricultural University, Software Institute, Taigu 030800, China;3. Arid Farming Research Center, Shanxi Academy of Agricultural Sciences, Taiyuan 030000, China)

【】Centrifuge is a common apparatus to measure soil water retention curve, but the resultant soil compression is an issue that might compromise its accuracy and reliability. The purpose of this paper it to present a method to correct such inferiorities.【】We measured the water retentions of 16 repacked soils with contrasting texture and organic matter (OM) taken from Shanxi province using a centrifuge apparatus. In the experiment, we measured the initial soil volume, dynamic soil volume, as well as water content under different spinning speeds. A multiple nonlinear regression model was derived to describe the dependence of the matric potential on volumetric moisture content, soil particle sizes, volumetric soil mass and OM; it was then verified against the experimental data. 【】The logarithm of the matric potential was linearly related to mass fractions of the sand, clay, OM and volume of the water. The accuracy of the model was 74%, with an average relative error of 14.460% for the modelled samples, and of 13.237% for the samples used for verification. It was also found that soil texture affected predictivity of the model. The matric potential was negatively correlated to the mass fraction of sand, volumetric soil mass and water content, but positively correlated to the mass fraction of clay and organic matter.【】The nonlinear regression model linking the matric potential to soil water content, with the change in soil volume modified, was able to improve the accuracy of the centrifuge method; it has implications in soil hydraulic parameter measurement.

soil water retention; multiple nonlinear regression model; centrifuge method; virtual numerical simulation

S152.7+1

A

10.13522/j.cnki.ggps.2019236

1672 - 3317（2020）01 - 0084 - 07

2019-09-08

山西省重点研发计划重点项目（201703D211002-2）；山西省科技攻关项目（20130311008-5）

任健（1995-），男。硕士研究生，主要从事土地信息技术研究。E-mail:549484055@qq.com

张吴平（1973-），男。教授，主要从事土地信息技术研究。E-mail:zwping@126.com

任健, 张吴平, 王国芳, 等. 基于离心机法获取定体积质量下的土壤水分特征曲线[J]. 灌溉排水学报, 2020, 39(1):84-90.

REN Jian, ZHANG Wuping, WANG Guofang, et al. Method to adjust the soil water retention curve measured using centrifuge apparatus [J]. Journal of Irrigation and Drainage, 2020, 39(1): 84-90.

责任编辑：陆红飞