基于椭圆傅里叶的产品外形意象设计

王 增，刘卫东，杨明朗，韩栋基

(1．南昌大学 机电工程学院，江西 南昌 330031；2．南昌大学 艺术与设计学院，江西 南昌 330031)

0 引言

在竞争日趋激烈的市场环境下，快速、准确地识别并满足用户情感需求是增强产品竞争力的关键，产品形态则是体现感性因素最直接的方式，产品外形意象设计已经成为企业重要的竞争力之一[1]。产品外形意象设计是以系统挖掘用户对产品的感性认知并将其转化为产品设计要素的感性工学技术(Kansei engineering)[2-3]为基础，研究将用户情感转化于产品外形上的设计模式，已经成为现代产品外形设计的研究热点。

目前关于产品外形意象设计的研究主要包括形态描述、感性意象定位、形态分析、产品感性意象和外形特征关联等环节[4]，可进一步归纳为如下两方面研究内容：①将形态描述、感性意象定位和外形优化结合的研究，如基于外形轮廓数值化描述的外形意象优化研究[5-8]；②将感性意象定位、形态分析、产品感性意象与外形要素关联相结合的研究，如基于形态分析的感性意象与外形特征参量的回归研究[9-11]。在具体研究中，产品形态描述环节常采用提取二维轮廓关键点坐标的方式进行外形的数值化描述[5-8,12]，该方法的数据获取方式简单直接，但获得的数据仅包含轮廓位置信息，存在记录和提炼形态信息能力不足，无法利用该数据概括外形重要特征的问题；感性意象定位环节多通过对样本感性意象的主观评估数据进行关键感性意象定位[13-17]，虽然评分源于受测者对外形的感觉判断，但是仅依靠主观评分而完全脱离外形实际数据的定位方式客观性不强，且在词汇合并过程中存在感性意象信息丢失，易造成关键感性意象定位不准、覆盖范围不全和重要程度不明等问题，不能有效满足产品外形设计前期需先确立若干重要程度不同的关键感性意象这一外形设计目标的实际要求；形态分析环节常将产品形态解构为项目和类目等外形特征参量来开展意象分析[11,13,16-21]，然而因为特征参量间并不完全独立，例如形态各角度等空间角度参量与高宽比、面积周长比等空间距离参量[10]都存在一定的相互关联，且形态的整体意象具有视觉优先性[17]，所以直接用局部的外形特征组合较难准确解析用户感性意象，导致在产品感性意象与外形特征关联环节所得回归模型的拟合精度不高，不利于准确评价和优化创意外形方案。

椭圆傅里叶描述子(Elliptic Fourier Descriptors，EFD)通过将形状特征空间定义为复平面来描述二维空间曲线[22-23]，已广泛应用于信号分析、生物和遥感地貌识别、服装工程等领域[24-27]。相对于点坐标数值化的常用外形描述方法，椭圆傅里叶方法调整拟合轮廓的方式更具整体性，随着每一频次谐波的叠加，带来的是拟合轮廓整体而非局部性变化，进而通过不断增加谐波频次逐渐逼近原始轮廓。鉴于椭圆傅立叶方法对自由和复杂的形态具有良好的描述和形态分析能力[4,26,28]，并可通过主成分分析(Principal Component Analysis，PCA)得到包含形态信息的主成分数据[29-30]，该数据不仅可以用于已有的形态识别与分类研究，还有望解决当前产品外形意象设计研究存在的上述问题，本文首次将椭圆傅立叶方法应用于产品外形意象设计研究领域，利用该方法在描述和提炼外形信息的优势开展产品意象设计，形成新的感性意象综合评分模型和主成分评价模型，构建一套系统的产品外形意象设计研究方法，为设计师开展产品外形意象设计提供更有效的帮助，具体研究体系如图1所示。

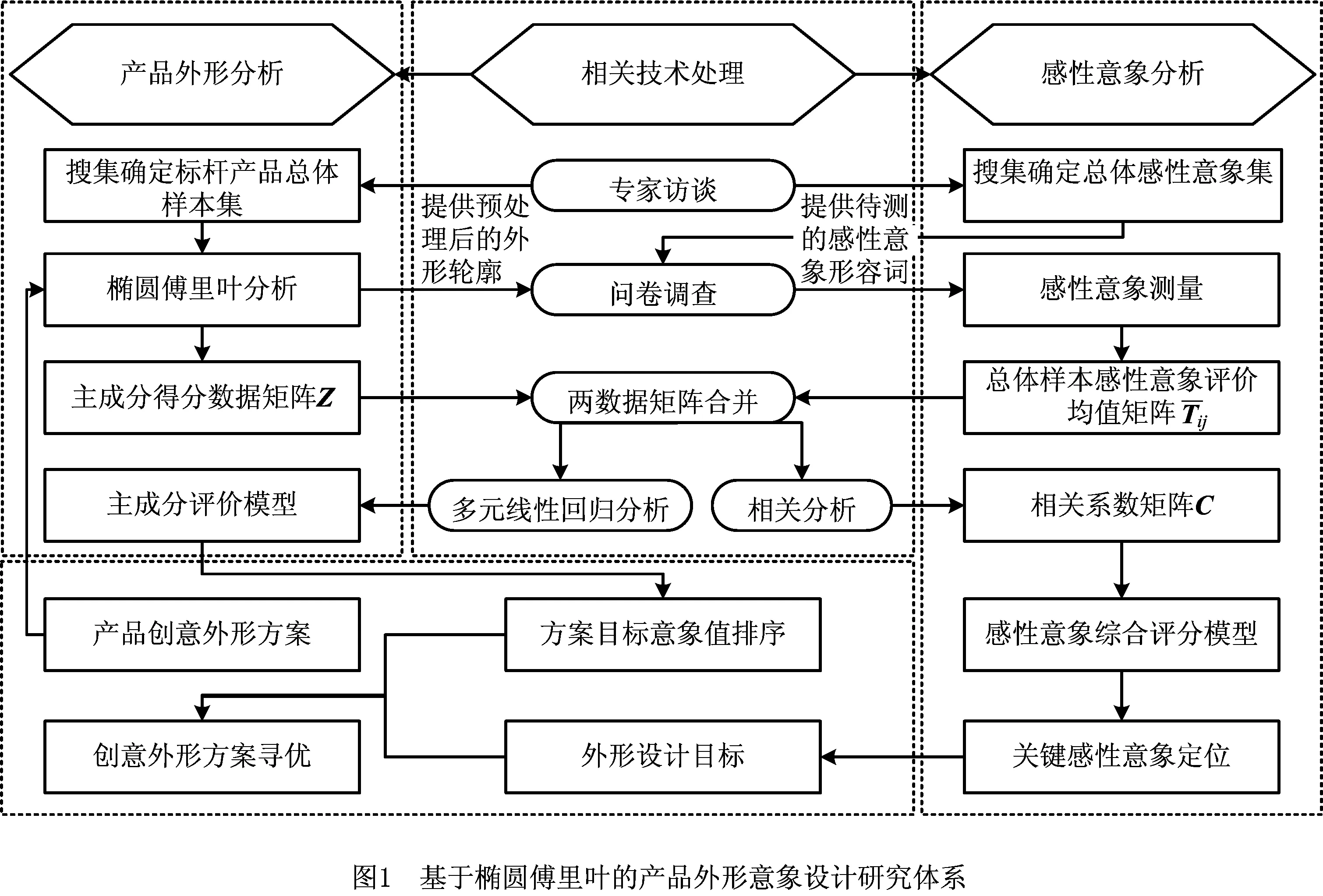
1 椭圆傅里叶分析

产品外形的椭圆傅里叶分析要先对产品外形方案图稿进行数字图像预处理，提取外形轮廓的边界坐标并将坐标转换为复坐标函数，经等距插值生成标准化的新插值点坐标序列，然后用椭圆傅里叶级数展开该序列，计算出可描述和重建外形轮廓的EFD系数矩阵，最后对该矩阵进行主成分分析，得到提炼了外形轮廓信息的主成分得分系数矩阵，具体过程如图2所示。

1.1 图像预处理与复坐标函数转换

图像预处理的具体流程为：先将产品图稿经过二值图像、平滑处理和阈值分割后，滤除图像背景的非目标信息，再提取产品的轮廓边界特征(如图3)，得到以轮廓边界某点为起始点，沿顺时针或逆时针方向绕边界一周，由a个离散采样点的x，y坐标组成的二维轮廓点坐标序列，该序列描述了样本产品外形轮廓的形状特征，表示为(x(i),y(i))，i= 0, 1,…,a-1。该轮廓的中心坐标可进一步表示为

(1)

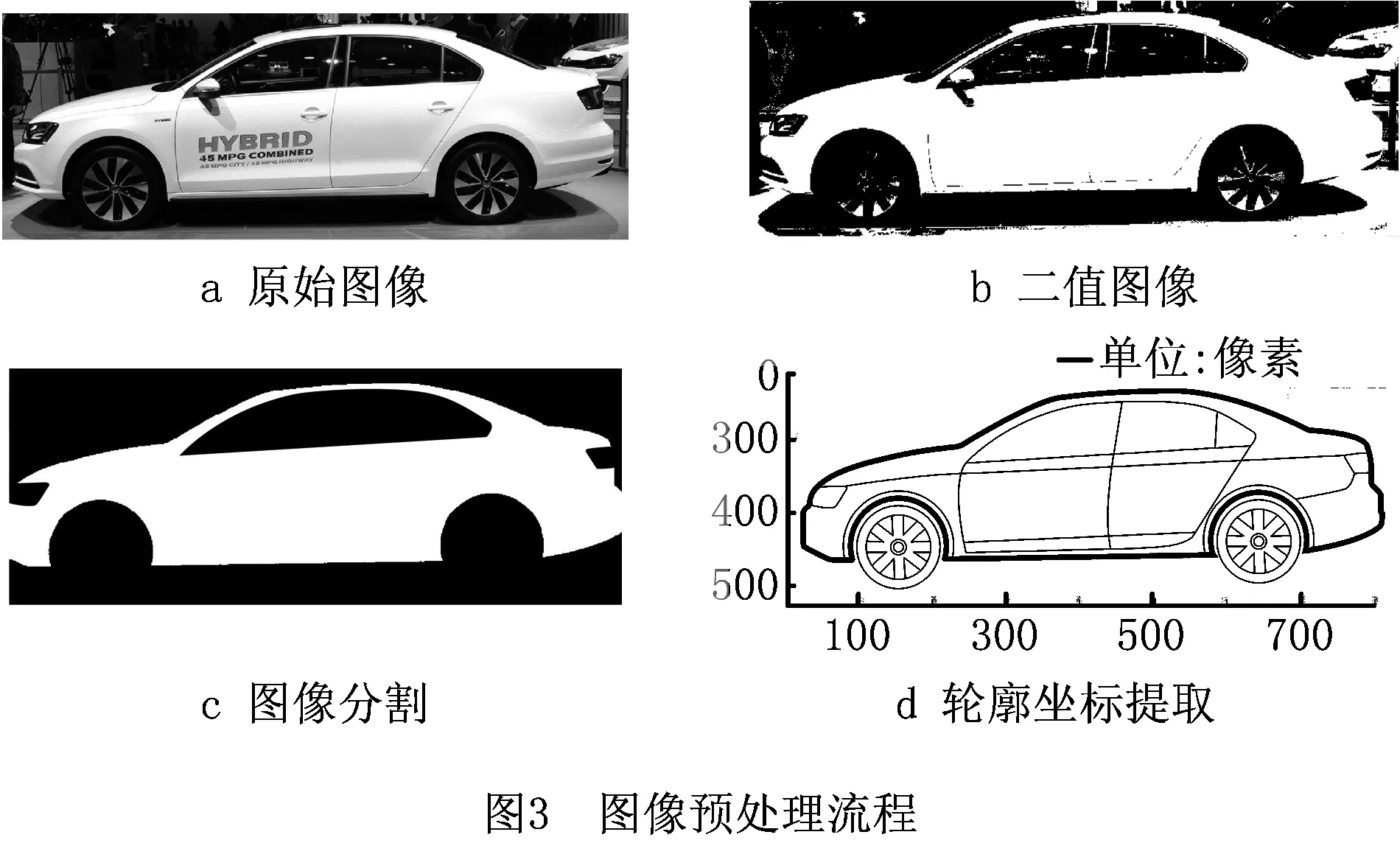
为便于后续椭圆傅里叶变换，用一个复函数关系式将二维轮廓点坐标序列表示为

z(i)=x(i)+jy(i)。

(2)

消除偏心后为

z(i)=[x(i)-xc]+j[y(i)-yc]。

(3)

1.2 标准化插值

为标准化不同样本数据点，在复坐标系下采用等距原理标准化插值。假定统一的新插值点数为A，样本形态边界轮廓的周长为

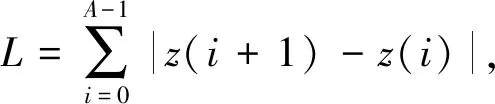
(4)

则等弧长采样间距为

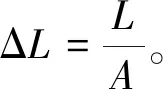
(5)

假定第s个新插值点位于原轮廓点z(m)和z(m+1)之间，原轮廓点z(m)到起始点的距离为

(6)

则第s个新插值点到起始点的距离为

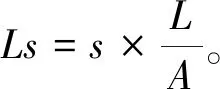
(7)

根据两点间任意一点的坐标求解公式

ω=(1-α)ω1+αω2，0≤α≤1。

(8)

式中：ω为所求点的x或y坐标，ω1和ω2为已知两点的x或y坐标，α为所求点到两点间的距离之比。则新插值点数据序列z(s)表示为

(9)

1.3 椭圆傅里叶描述子计算

z(s)表示一条周期为T的曲线，根据周期函数可用傅里叶级数展开的性质，将z(s)在复平面实轴和虚轴的投影用椭圆傅里叶级数展开为

(10)

(11)

式中A为新插值点数，4个系数与同一谐波频次n对应。这样，任意封闭的轮廓可用一组包含n个谐波频次的椭圆傅里叶系数描述为

(12)

式中F为EFD系数矩阵，它通过控制具有四维参数的椭圆谐波频次n来逼近物体的轮廓曲线。当n取不同值时，轮廓曲线的拟合效果将出现差异，具体表现为低频次谐波影响轮廓的整体特征，高频次谐波影响轮廓的局部细节。

1.4 主成分分析

PCA是将多个相关原始变量降维成少数不相关新变量的有效方法，该方法能够尽可能保留原始变量信息，简化并揭示原始变量数据间的内在联系。为此，在采用椭圆傅里叶方法对数量为Q的总体样本外形轮廓展开描述并得到矩阵F的基础上，采用PCA将矩阵F降至m维，此时各主成分累积方差贡献率达到某设定值，对应的总体样本主成分得分矩阵

(13)

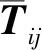
2 感性意象与外形优化

感性意象是人对物所持有的感觉，是对物的心理上的期待感受，是一种高度凝聚的深层次的人类情感活动[31]。产品外形的感性意象则是人对产品外形整体及要素的综合认知，为利用感性意象开展外形优化设计，本文从感性意象测量、总体样本的关键感性意象定位和个体方案的主成分评价模型构建与外形优化3个方面进行研究。

2.1 感性意象测量

调研搜集适合描述样本外形的感性意象形容词，经专家访谈后确定总体感性意象集，用语义差异法和7点李克特量表法量化表征各形容词，再结合各样本预处理后的外形轮廓制成感性意象调查问卷，让受测者对各样本外形轮廓的感性意象进行问卷评价。在对问卷进行测量与回收统计后，可得个体受测者的感性意象评分矩阵

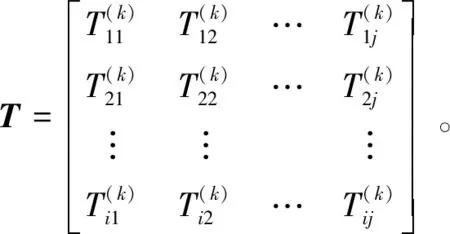
(14)

式中：i为样本编号，j为各感性意象形容词对编号，T(k)ij为第k个受测者对第i个样本的第j个感性意象形容词对的评分值。

进一步求出全体受测者的评分均值矩阵

(15)

式中K为受测者总数。

2.2 感性意象综合评分模型构建与总体样本关键感性意象定位

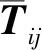
(1)删除无显著相关的感性意象形容词

相关系数矩阵C存在非常显著相关、显著相关和不相关3种显著性水平，其中P<0.05表示两者显著相关，将与所有主成分全部不相关，即显著性水平P≥0.05的感性意象形容词剔除后，余下全为关键感性意象。

(2)构建总体样本的感性意象综合评分模型

为按重要程度排序各关键感性意象，给矩阵C中各相关系数的不同显著性水平赋予乘数系数λ(λ=0，1，2)，构建感性意象综合评分模型

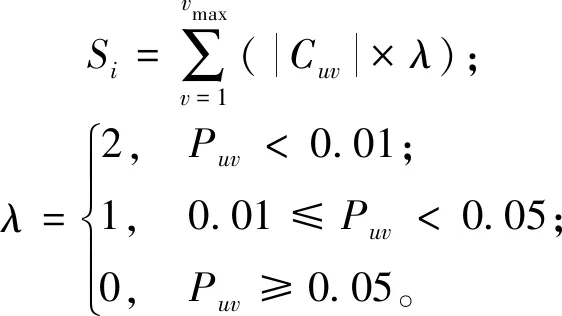
(16)

式中：u为感性意象形容词个数，v为主成分数，vmax为最大主成分数，Cuv和Puv分别为第u个意象形容词与第v个主成分的相关系数和显著性水平，Su为第u个形容词的总体样本感性意象综合评分。由于各主成分凝练了总体样本轮廓的外形信息，感性意象和主成分的相关系数客观表征了感性意象与外形的联系情况，因此Su值可保证后续总体样本关键感性意象定位的客观性和准确性。

(3)定位总体样本的关键感性意象

由式(16)计算各感性意象形容词的Si并由高到低排序，排序情况反映感性意象的重要程度。相比目前的常用定位方法，本文定位方式更为客观和准确，可定量计算所有关键感性意象的重要程度并排序，全面保留影响外形设计的关键意象信息，有助于在设计前期通过对标杆产品总体样本的关键感性意象进行定位来准确设定具有不同重要程度的多意象外形设计目标，为设计师解决外形意象设计中面临的实际问题提供参考。

2.3 个体方案主成分评价模型构建与外形优化

经过总体样本的关键感性意象定位确立外形多意象设计目标后，在实际设计中，需要对个体创意外形方案展开感性意象评价，以判断其是否达到外形设计目标。为此，需要通过主观感受和设计元素的关系、形态规则和产品语意之间的关系构建感知空间[32]，该感知空间即外形意象评价模型。本文针对个体创意外形方案的评价构建了主成分评价模型，具体步骤如下：

(1)根据总体样本关键感性意象的定位情况和设计项目实际要求选取多目标意象。

(2)根据与各目标意象的相关系数显著性水平值确定关键主成分

X′={x′/P(x′)<0.05,

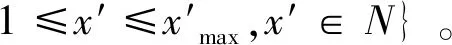
(17)

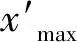
(3)以各目标意象值为因变量，与各目标意象对应的关键主成分得分为自变量，建立主成分评价模型

(18)

式中：w为各目标意象，y(1)(w)为各目标意象值，k为关键主成分的个数，r(1)(w)和α(1)wk分别为各目标意象主成分评价模型的拟合残差向量和回归系数，x(1)wk为各目标意象对应的各关键主成分得分。

(4)采用两个最常用的信息检验模型——赤池信息准则模型[33](Akaike Information Criterion，AIC)和贝叶斯信息准则模型[34](Bayesian Information Criterion，BIC)，与目前常用评价模型进行比较，证明主成分评价模型的优势。计算模型的AIC和BIC值(IAIC,IBIC)：

L=-D/2×(1+log(2×pi)+log((r′×r)/D))；

(19)

IAIC=-2×(L/D)+2×k/D；

(20)

IBIC=-2×(L/D)+k×log(D)/D。

(21)

式中：L为模型的对数似然函数值，r为拟合残差，D为样本容量。IAIC和IBIC值越小，模型越优良。

(5)将个体创意外形方案的EFD数据加入标杆产品总体样本的描述子数据矩阵并计算其主成分得分。因为加入个体方案对标杆产品总体样本主成分得分矩阵的数据扰动非常微小，可忽略不计，所以将与各目标意象对应的个体方案的关键主成分得分代入主成分评价模型，求得该方案的各目标意象值，再依次计算其余创意外形方案的各目标意象值，完成对所有创意外形方案的感性意象评价。

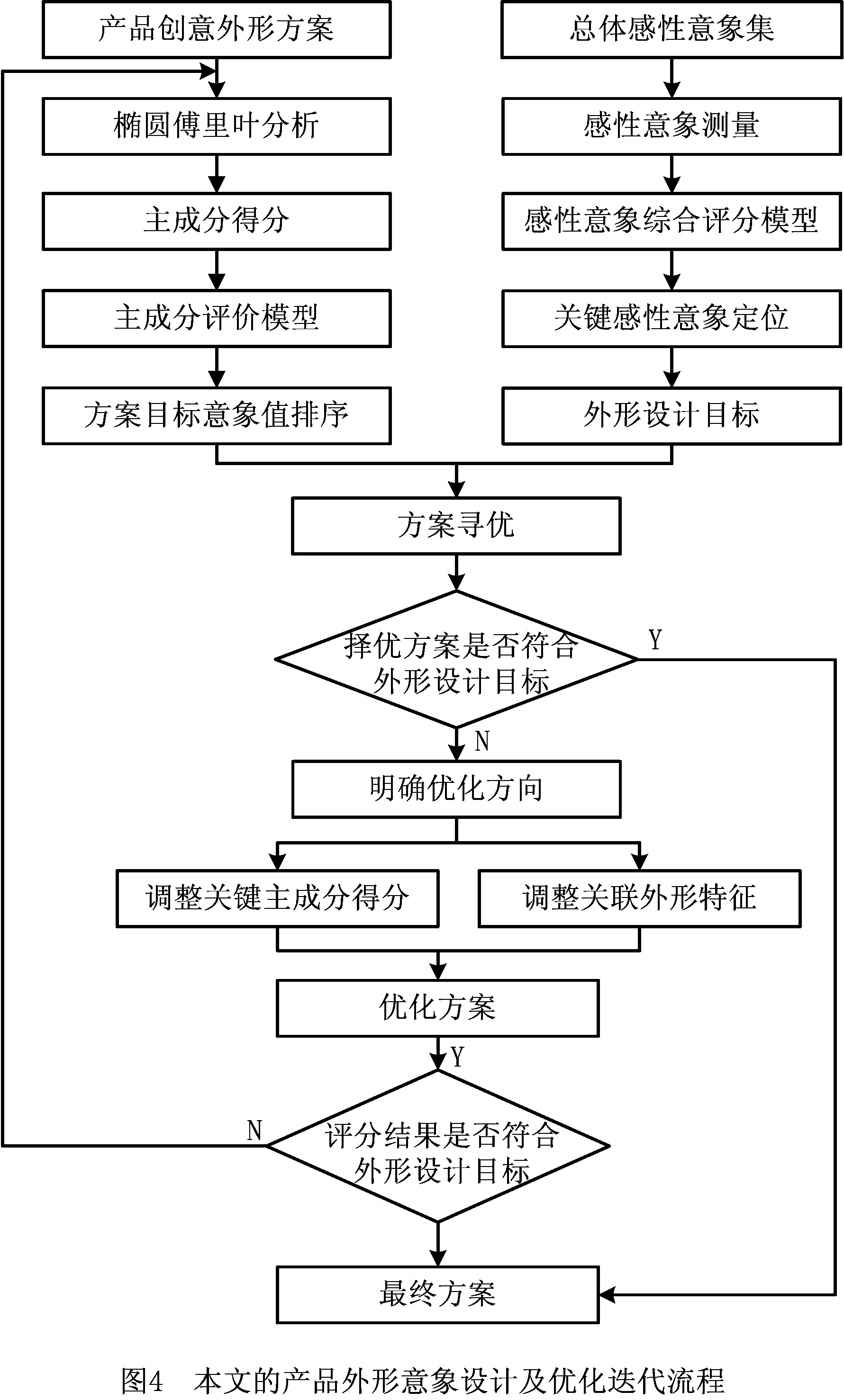
随后，参考外形设计目标开展方案寻优，确定择优方案。若择优方案仍不满足外形设计目标，则对比差异性后，改变择优方案的关键主成分得分，重新拟合生成新的外形方案，并进一步通过调整与目标意象相关的关联外形特征来优化新方案。在此过程中，先对总体样本的主成分得分进行正态性检验，由于总体样本的主成分得分满足正态或近似正态分布，根据正态分布的特点，以总体样本各主成分得分的均值及均值±3倍标准差数据分别拟合外形轮廓，该轮廓组合图能够反映样本99%的外形特征变化规律。通过该图把握各主成分的关联外形特征，再结合反映主成分与感性意象关系的相关系数矩阵C得到目标意象的关联外形特征，至此设计师最终明确与目标意象对应的关键主成分得分的调整方向和关联外形特征的优化设计方向，在此指导下完成对创意外形方案的优化。让全体受测者评估该优化方案的感性意象并观察评估结果与外形设计目标是否一致，若不一致则反复迭代该设计过程，直至生成评估结果为与外形设计目标一致的方案。具体的产品外形意象设计和优化迭代流程如图4所示。

3 应用研究

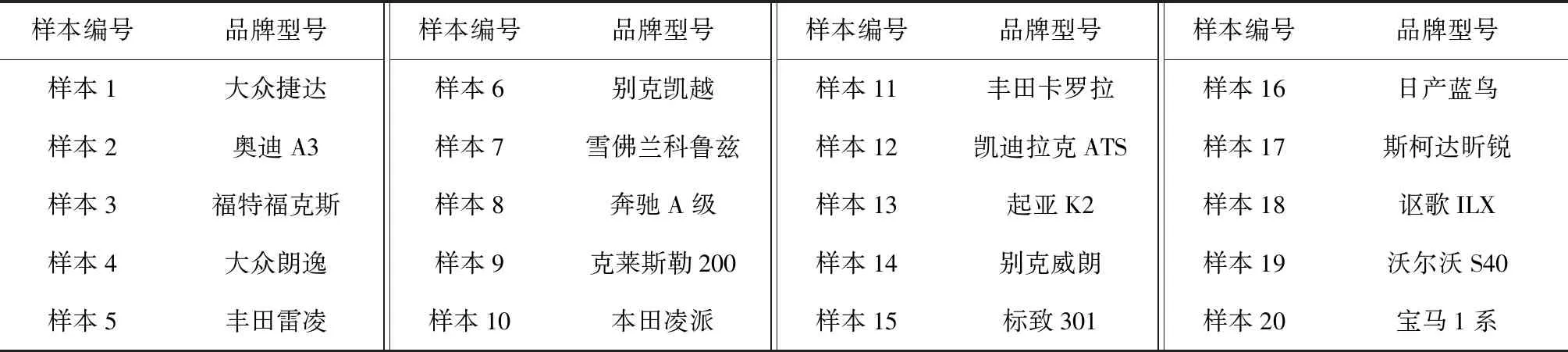
外形意象是汽车外形设计极为关键的内容，在此将上述方法应用于汽车侧面外形意象设计，以验证方法的有效性。首先，广泛搜集各类汽车正侧面视图，得到50个品牌旗下共250份汽车样本，参照德国汽车工业对本文标杆车产品，即A级三厢轿车的分级标准，根据轴距和排量等参数剔除不符合标杆车产品的图片后保留180份样本；其次，对样本编号并随机抽取其中的90份样本，统一去色后交由5位资深的工业设计教师进行完整浏览，并按外形相似度分类，在每类中选择一个最具代表性的样本；最后，在保证汽车样本外形区分度和品牌差异性的基础上，保留20份样本形成标杆车总体样本作为本文的研究对象，具体样本、品牌及型号如图5和表1所示。

3.1 椭圆傅里叶分析

汽车侧面外形轮廓线涵盖的设计要素较多，属于典型的复杂设计问题[35]，参考众多汽车外形意象设计研究中选取汽车侧面轮廓线作为研究对象[5-7,35-38]，本文的研究重点为底盘以上部分轮廓的主外形特征线[36]，即由前引擎盖顶端线、车厢顶端线和尾箱顶端线共同组成的侧面轮廓线。在提取各样本汽车侧面轮廓线的基础上，给各样本侧面轮廓线叠加同一外形且线型较细的轮毂、车灯、腰线、门框等次要设计要素线框，形成较完整的以侧面轮廓线为核心特征的汽车侧面外形意象研究对象，以使研究成果符合工程实际。轮胎位置和底盘对感性意象的影响可忽略，因此固定不动[6]。先对样本图

表1 20份研究样本的品牌型号

样本编号品牌型号样本编号品牌型号样本编号品牌型号样本编号品牌型号样本1大众捷达样本6别克凯越样本11丰田卡罗拉样本16日产蓝鸟样本2奥迪A3样本7雪佛兰科鲁兹样本12凯迪拉克ATS样本17斯柯达昕锐样本3福特福克斯样本8奔驰A级样本13起亚K2样本18讴歌ILX样本4大众朗逸样本9克莱斯勒200样本14别克威朗样本19沃尔沃S40样本5丰田雷凌样本10本田凌派样本15标致301样本20宝马1系

稿进行数字图像预处理，提取其侧面外形轮廓和坐标。因为各样本轮廓点数约为500，所以式(11)选择A= 512进行标准化插值处理。然后，根据式(1)～式(9)计算得样本轮廓的新插值点数据序列z(s)，对z(s)进行椭圆傅里叶级数展开，可得表2所示的EFD系数矩阵。

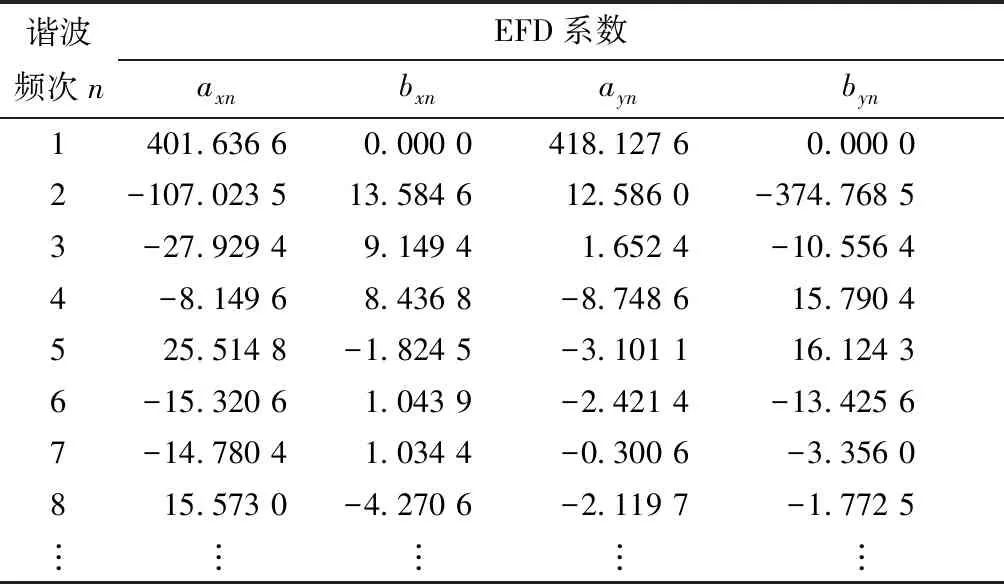
表2 某样本汽车侧面外形轮廓的EFD系数(部分)

将该矩阵通过傅里叶逆变换来拟合样本的侧面外形轮廓，观察椭圆傅里叶方法的拟合效果。以某样本汽车为例，图6所示为其在不同最大谐波频次N下的拟合情况，由于汽车轮廓曲线连续光滑，拟合曲线在较少谐波频次下就可以很好地逼近原轮廓。

为确定最大谐波频次N，计算随机抽取样本在不同谐波频次n下拟合曲线和原始轮廓上对应点间距离的平均值、最大值和标准差，即均值误差、最大误差和误差标准差，如表3所示。

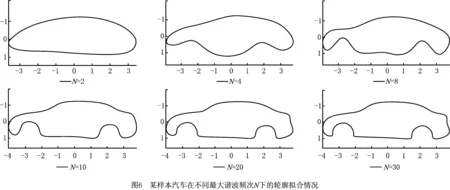
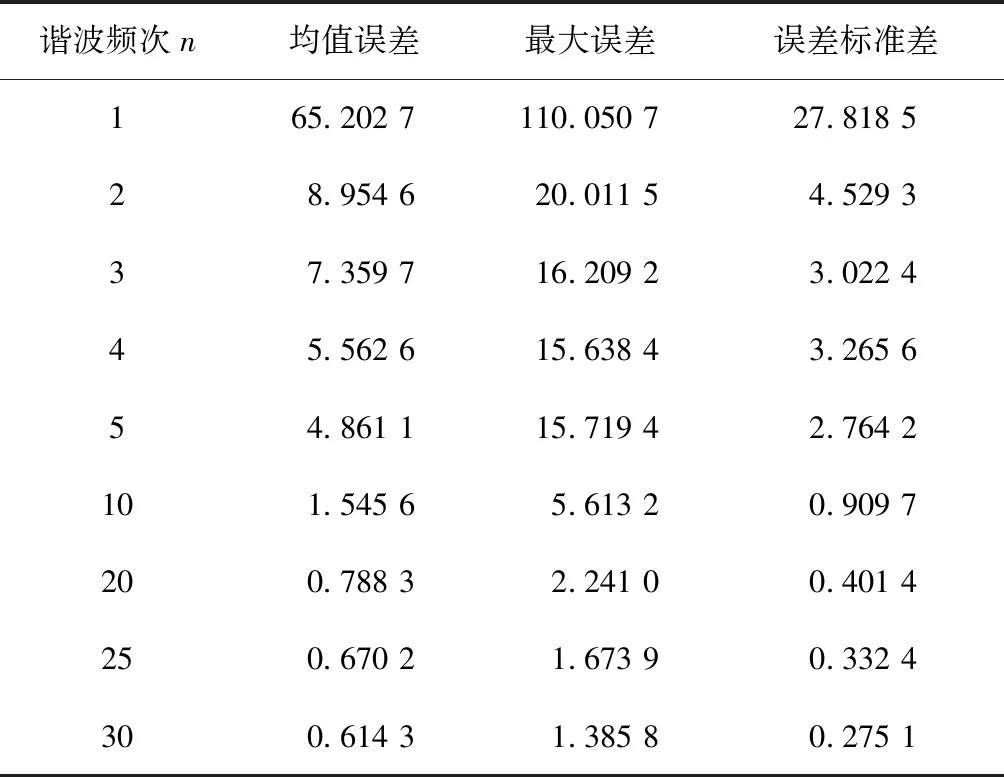
表3 某样本汽车侧面外形轮廓的椭圆傅里叶拟合误差数据(N=30)

图7所示为该样本汽车在不同最大谐波频次N下的三项拟合误差数据折线图，可以直观地反映误差的变化趋势：随着最大谐波频次的增加，椭圆傅里叶方法的三项误差均快速收敛，在最大谐波频次N=30时达到满足研究精度所需的误差最小范围，此时最大误差小于1.4 mm，均值误差小于0.7 mm，误差标准差小于0.3 mm，且误差保持相对稳定。因此，确定最大谐波频次N=30。

进一步绘制20份标杆车总体样本的均值误差折线图(如图8)，从统计学层面再次确认所选定的最大谐波频次，并证明椭圆傅里叶方法用于描述不同样本外形轮廓具有稳定性。

采用N=30获取总体样本的EFD系数矩阵，再用PCA法对矩阵降维，得到总体样本的主成分得分矩阵Z(如表4)，进一步结合不同主成分数的轮廓拟合效果和方差贡献率确定最大主成分数。

图9所示为对随机抽取样本用不同主成分数拟合侧面外形轮廓的效果。可见主成分1已经能较好地描述原样本轮廓的整体特征，仅在局部细节与原轮廓存在差异。随着主成分数的增加，拟合曲线在不同局部进一步与原轮廓接近，说明其他主成分对轮廓局部也有明显影响。结合表5所示的各主成分方差贡献率可知，当增加到9个主成分数时，累计方差贡献率达到99.99%，此时拟合轮廓与原轮廓重合，即20份总体样本的EFD系数矩阵可以降维至9个主成分的得分矩阵来表达。

表4 总体样本的主成分得分矩阵Z

表5 各主成分方差贡献率 /%

3.2 感性意象测量与总体样本关键意象定位

从当前研究汽车外形意象设计的论文、杂志、广告和咨询专业人士，搜集适合描述汽车外形的感性意象形容词共计45个，经专家访谈筛选后保留26个，结合样本预处理后的侧面外形轮廓，制成如图10所示的汽车侧面外形轮廓意象调查问卷。

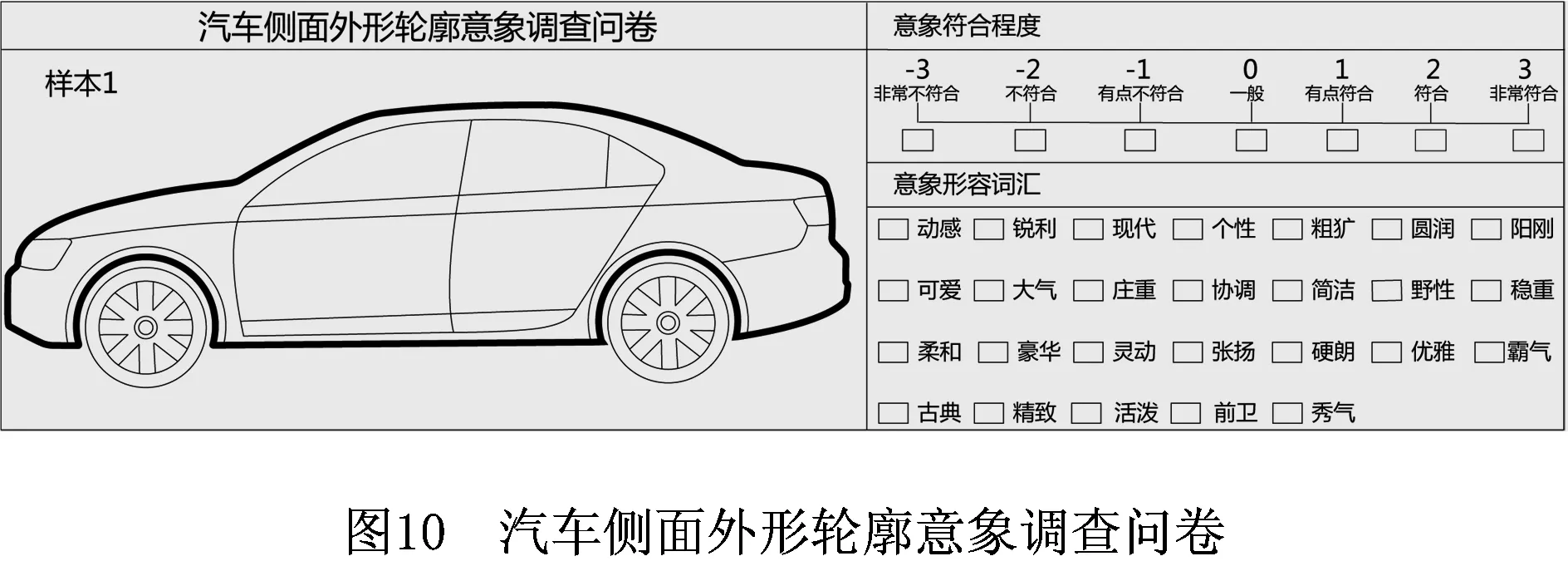
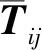
表6 总体样本感性意象评价均值矩阵

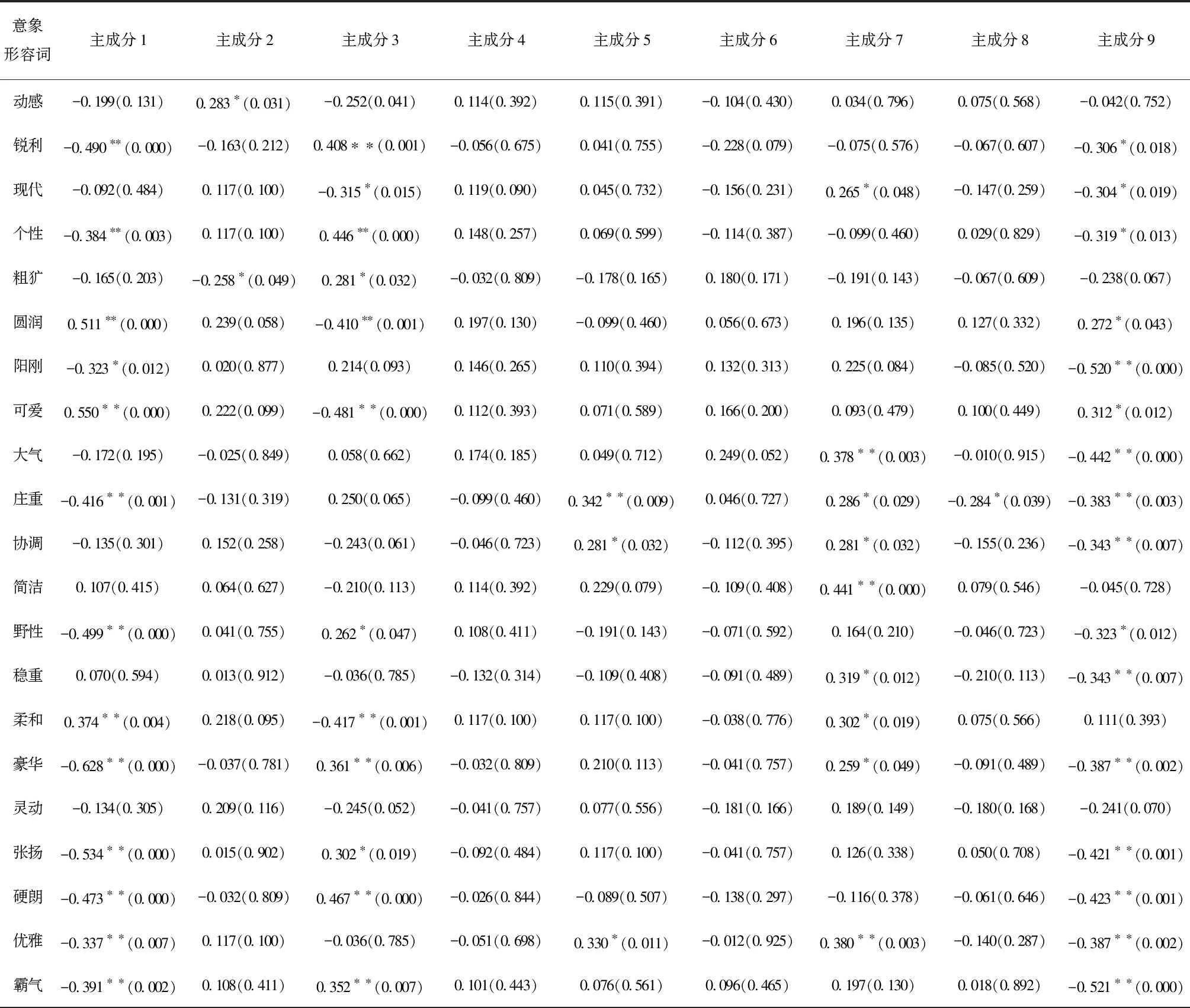
表7 各主成分与各感性意象形容词的相关系数矩阵C

续表7

注：括号内为显著性水平P值，*表示P<0.05显著性差异，**表示P<0.01非常显著性差异。

删除无显著相关的感性意象形容词“灵动”，得到关键感性意象形容词25个。根据感性意象综合评分模型计算各关键感性意象的综合评分Si并排序，结果如表8所示。

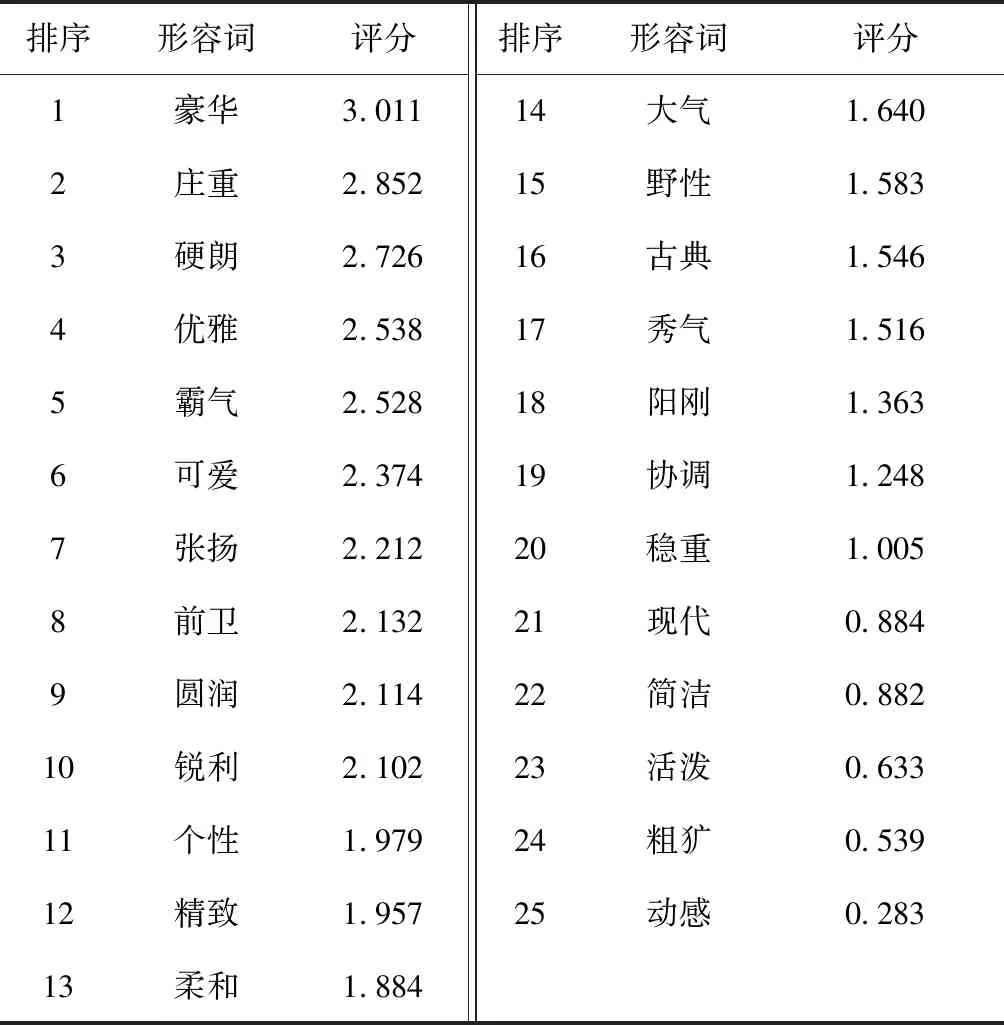
表8 总体样本关键感性意象的综合评分及排序

采用目前常用的聚类分析方法可定位得到“豪华”、“硬朗”、“前卫”、“柔和”与“简洁”5个关键感性意象。显然，该定位不能全面覆盖总体样本的关键感性意象，也无法反映各意象的重要性排序情况，不利于确立一个清晰且符合实际设计要求的外形设计目标。在此基础上，进一步取本文方法所得的前5个关键感性意象与其进行比较。因为感性意象评分值为0表示该意象形容词及其反义词均不适合表征样本，所以0分值的出现频次可反映该感性意象对于总体样本描述的符合程度，该值越高，说明该感性意象越不具有代表性。表9所示的统计结果表明，除豪华与硬朗外，目前常用方法中另外3个感性意象的0分值出现频次均高于本文方法定位的3个感性意象，证明其定位不如本文方法准确。

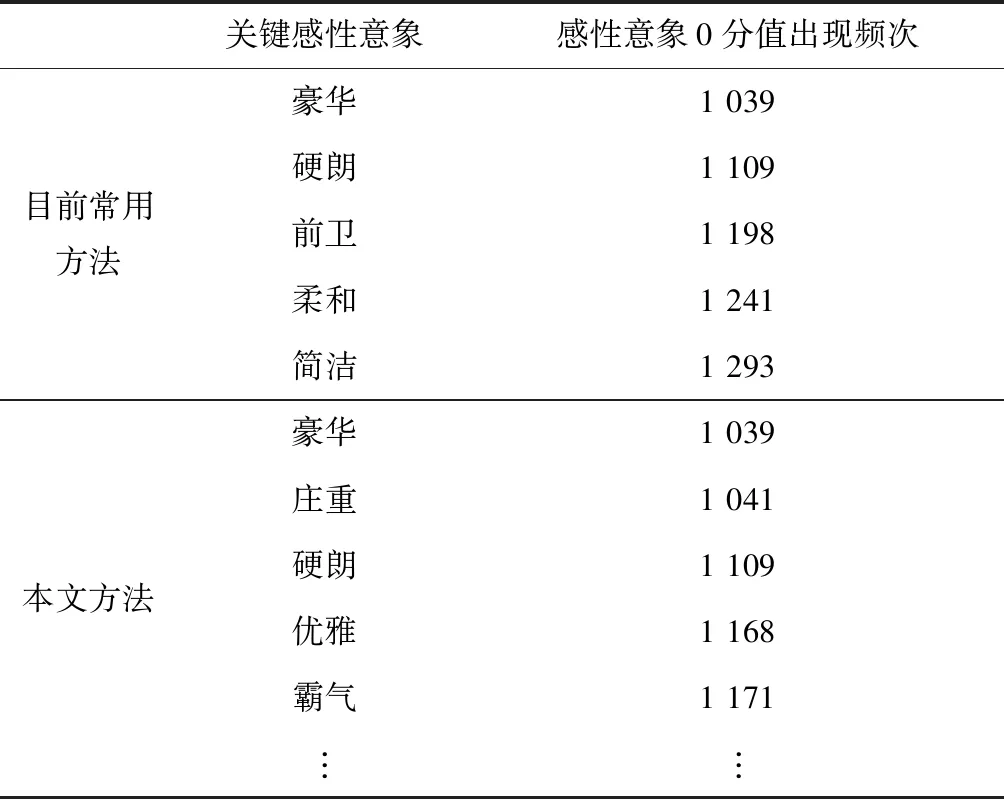
表9 意象定位结果比较

根据本文的定位结果，明确外形设计目标中的关键感性意象项目及其重要性排序为“豪华”、“庄重”和“硬朗”，以此作为汽车侧面外形设计方案的目标意象。

3.3 个体样本的主成分评价模型构建与评价

采集图11所示的样本侧面外形轮廓的高宽比和面积周长比等空间距离参量，以及前风挡夹角、前引擎面夹角、后风挡夹角和后备箱面夹角等空间角度参量。

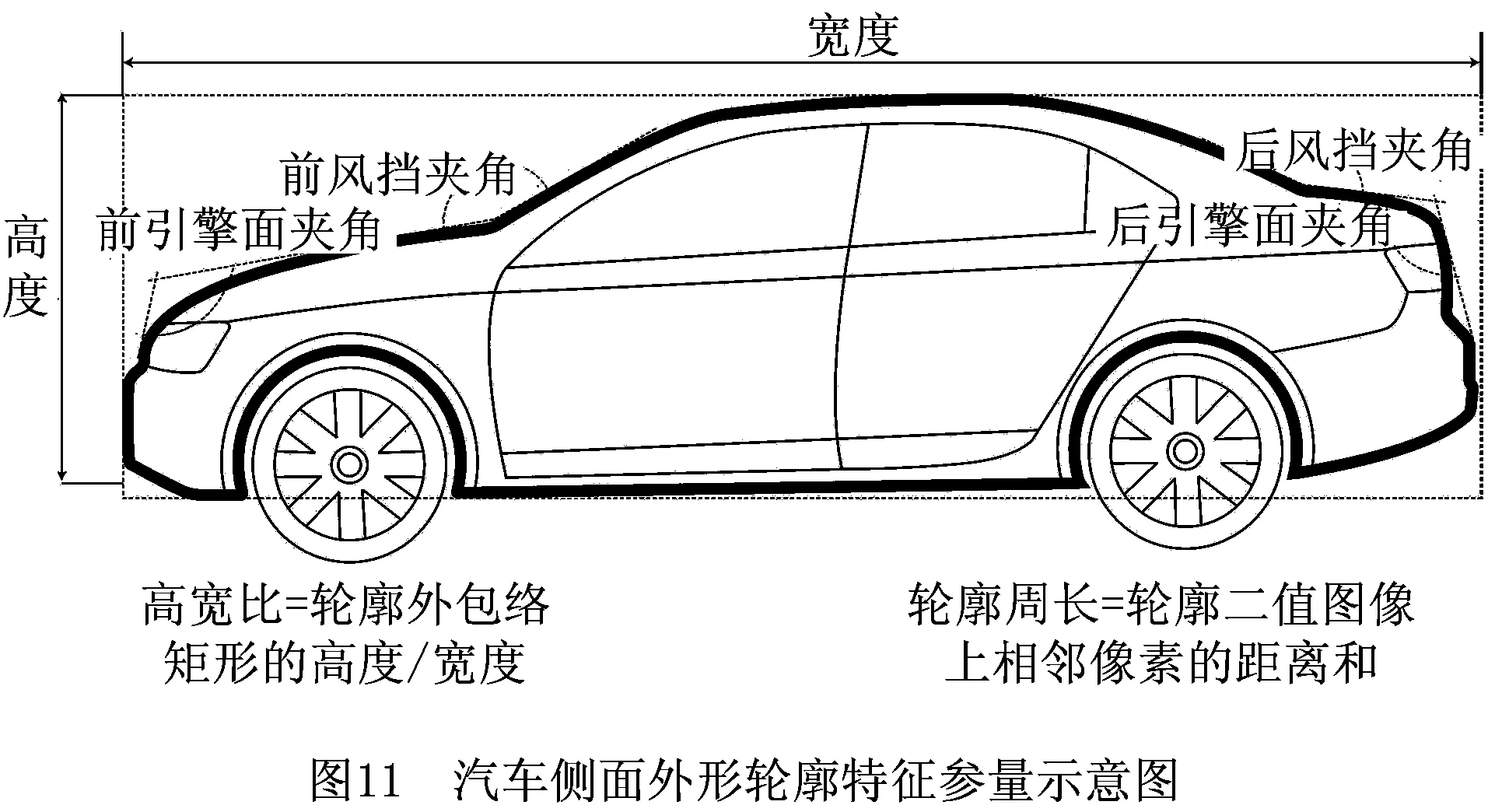
以各目标意象为因变量，上述外形特征参量为自变量，构建目前的常用评价模型，并按式(17)和式(18)构建主成分评价模型。两个模型的样本容量D均为总体样本数20，限于篇幅，以“豪华”感性意象为例展示两种模型：

(1)主成分评价模型

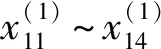
(2)所有外形特征参量评价模型

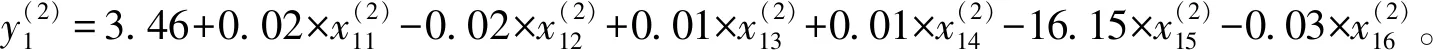
将两种评价模型数据代入式(19)～式(21)计算IAIC和IBIC值，得到IAIC1=2.662，IAIC2=2.715，IBIC1=2.874，IBIC2=2.924。

按照相同方法求得其余各关键感性意象的评价模型，并计算IAIC和IBIC值，结果如图12所示。

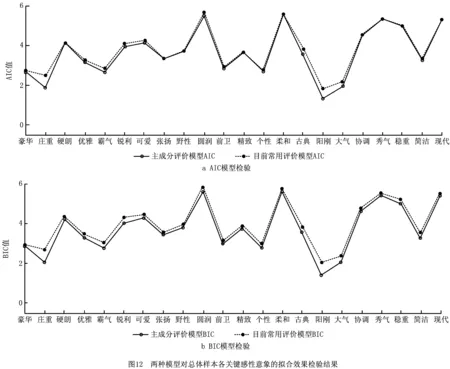
AIC和BIC模型均证明，主成分评价模型通过优选关键主成分作为拟合变量，提高了感性意象评价模型的精度，对所有关键感性意象的拟合效果均优于目前的常用评价模型。至此，确定用主成分评价模型对个体创意外形方案进行感性意象评价。

分别将3款汽车创意外形方案的EFD数据加入标杆车总体样本描述子数据矩阵并计算主成分得分，使用主成分评价模型计算3款方案的目标意象评分值，结果如表10所示。

对比外形设计目标进行3款创意外形方案寻优，方案1的“豪华”和“硬朗”意象值最高，确定方案1为择优方案，其与外形设计目标存在的差异是“庄重”和“硬朗”的重要性顺序不同，为此需进一步优化该方案，在尽量不弱化“硬朗”意象值的基础上增加“庄重”意象值。

表10 3款创意外形方案及其目标意象评分

3.4 择优方案的外形优化与评价

图13所示为总体样本各主成分得分均值及均值±3倍标准差数据拟合出的轮廓外形组合。表11所示为图8反映的各主成分关联外形特征，并对相关系数矩阵C中体现的感性意象项目及其强弱进行汇总与排序。

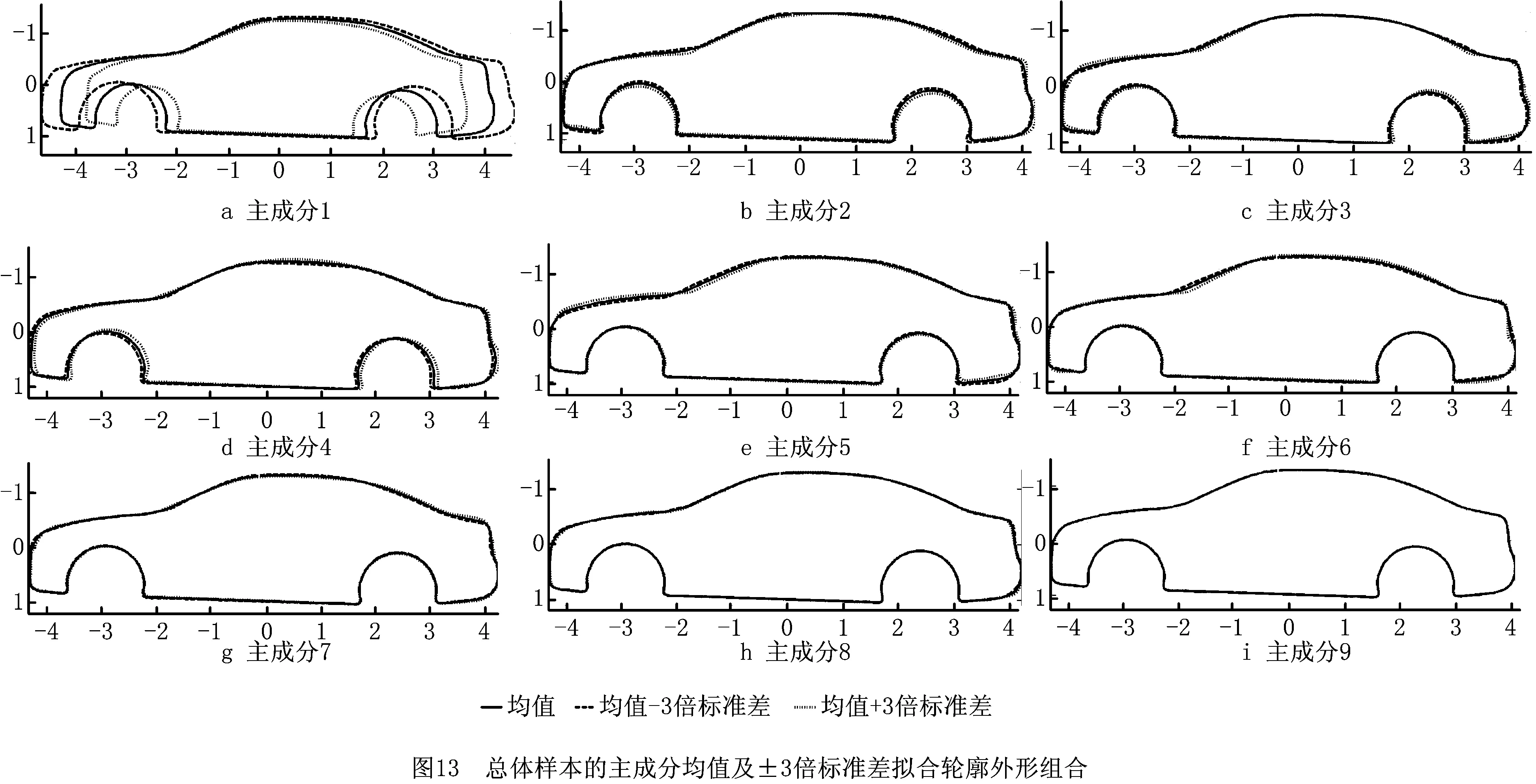
表11 各主成分关联的关键感性意象和外形特征

主成分关联关键感性意象关联外形特征主成分1正相关:可爱∗∗>圆润∗∗>柔和∗∗负相关:豪华∗∗>张扬∗∗>野性∗∗>锐利∗∗>硬朗∗>前卫>庄重∗∗>精致∗∗>霸气∗∗>个性∗∗>古典∗∗=秀气∗∗>优雅∗∗>阳刚∗∗扁平率、蓬松及收紧程度、整体轮廓线型主成分2正相关:活泼∗>动感∗负相关:粗犷∗蓬松及收紧程度主成分3正相关:硬朗∗∗>个性∗∗>古典∗∗>锐利∗∗>霸气∗∗>豪华∗∗>张扬∗>粗犷∗>野性∗负相关:可爱∗∗>柔和∗∗>圆润∗∗>现代∗>活泼∗前引擎面至车尾的轮廓上部曲线主成分4负相关:古典∗前引擎面、顶部至尾部面的轮廓上部曲线

续表11

结合图13和表11可知，在“庄重”感性意象的关键主成分中，主成分1和主成分9分别与“庄重”、“硬朗”显著相关，对其调整会同时引起两种意象变化；而主成分5和主成分8仅与“庄重”显著相关，适合用于此次对择优方案1的外形优化。根据主成分5和主成分8与“庄重”的相关关系，为增强“庄重”感性意象，通过适当增加主成分5并降低主成分8的得分来自动拟合生成新的外形优化方案4。在此过程中，基于设计师自身设计经验，参考与主成分5和主成分8紧密相关的关联外形特征，对优化方案4的A柱、车顶和轮廓曲线蓬松及收紧程度进行微调，最终生成满意的创意外形方案。让全体受测者对优化方案4的3个目标感性意象进行评分，然后统计评分均值，比较其结果与原方案1，如表12所示。优化后的方案4在“庄重”感性意象得分上有较为明显的提高，且3个目标感性意象的重要性排序与外形设计目标中的排序一致，从而实现了外形设计目标，将其确定为最终输出方案。

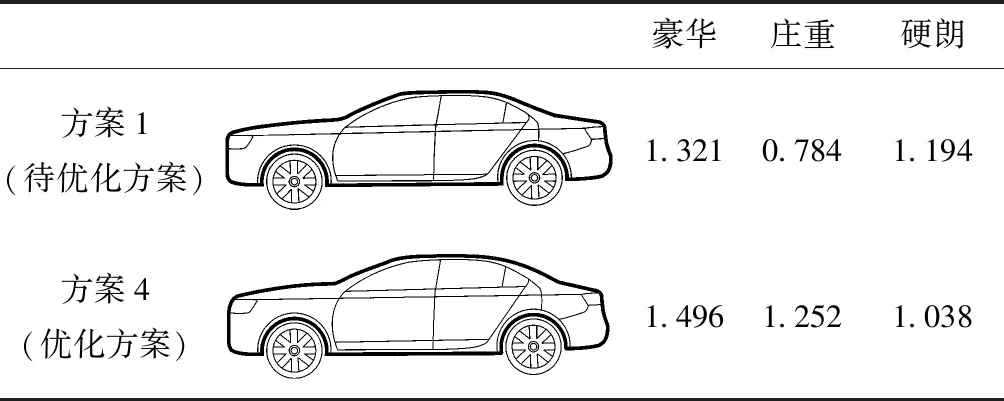
表12 创意外形方案4与方案1的感性意象比较

4 结束语

本文针对当前产品外形意象设计研究中存在的问题与不足，提出利用椭圆傅里叶方法对产品外形描述和信息提炼的优势来系统开展产品外形意象设计方法。经过椭圆傅里叶分析，提取到凝练外形特征信息的椭圆傅里叶主成分数据，对数据进行相关和回归分析，建立感性意象综合评分模型和主成分评价模型。利用感性意象综合评分模型对标杆产品总体样本进行关键感性意象定位，得到包括关键感性意象项目及其重要性排序的外形设计目标，以此作为创意外形方案的评价标准。在设计过程中，将创意外形方案的EFD数据加入标杆产品的总体样本描述子数据矩阵中计算主成分得分，再用主成分评价模型对创意外形方案进行评价和寻优，对比择优方案的排序结果与外形设计目标，找出二者间的差别，通过调整关键主成分得分和关联外形特征进行针对性的设计优化，对该设计过程进行迭代，输出满足外形设计目标要求的最终设计方案。最后，通过对汽车侧面外形意象设计的应用研究证明了方法的可行性。

本文丰富了产品外形意象设计研究的方法和技术体系，拓展了该领域的研究方式和手段，所提出的感性意象综合评分模型和主成分评价模型提高了感性意象定位和评价的准确性，为设计人员更好地开展产品外形意象设计提供了有效的方法和工具。进一步拓展椭圆傅里叶分析方法在产品外形意象进化、三维复杂产品外形意象及外形融合色彩意象等方面的设计应用模式，是笔者后续研究工作的重点内容。