面向功能需求的产品适应性修改单元识别方法
谢智伟,赵燕伟,任设东,桂方志
(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,浙江 杭州 310014)
0 引言
需求决定市场,同时也是产品设计或修改的驱动力,需求驱动下的产品适应性设计已经成为企业响应市场及满足客户的重要方法。产品适应性设计大致分为初始化设计和修改设计两类,前者侧重于在产品设计初期就考虑用户变化的需求及产品工况的改变[1-2],并将该设计理念融入产品的全生命周期,后者侧重于对已有实例产品的更改设计[3-4]。产品适应性修改以用户需求为驱动,通过对实例库检索得到的产品实例或用户指定的实体产品实施内部修改来满足用户功能性需求。
在机械领域中,产品、设备等一般都是多零件集成的复杂装配体,其内部关系交织错综,要实现对其内部单元的修改设计,一是要分析各单元的修改效应传导过程及其传导程度,二是在效应传导程度的指导下进一步选择传导程度较小的产品修改单元,以帮助企业实现产品修改变更的利益最大化。目前,国内外学者对工程领域修改变更设计的研究还处于上升期。Giffin等[5]通过分析大型数据集对复杂技术系统的变更传播效应进行预测;Koh等[6]提出一种工程变更传播效应的评估方法;Yin等[7]提出一种面向设计变更模型定义的方法(Design Change oriented Model-Based Definition, DCMBD),以有效管理工程变更;Masmoudi等[8]针对二维几何产品模型的变更,提出一种两步法的变更预测方法;杨煜俊等[9]提出面向产品结构的变更设计流程;唐敦兵等[10]结合设计结构矩阵建立了工程变更影响的分析及预测模型;宫中伟等[11-12]对工程变更设计中的关键Hub节点进行了分析研究,在后续工作中又构建了联系依赖矩阵以预测工程变更的雪崩传播;王祯[13]提出一种本体的方法对设计知识进行关联表达,从而分析工程变更的影响范围。
现代企业在产品设计中大多是以用户需求为驱动,以产品实例为修改母本的适应性修改设计,在适应性修改前期工作中,需要明确产品内部单元修改产生的效应传导程度并确定较小传导程度影响下的优先修改单元,上述文献对变更设计的传导影响进行了评估和预测,但对变更驱动力和工程产品之间的对应关系研究比较模糊,在对产品内部单元具体传导影响程度的量化计算及通过传导影响程度指导修改方案的制定上有待深入研究。鉴于此,本文提出一种产品修改单元的识别方法,以用户的功能性需求作为实例修改的驱动源,构建需求—产品之间的功能量化匹配模型,结合可拓理论的形式化模型表达,以基元有向图的形式实现产品组织的图论化表示,并给出了产品内部单元综合传导影响程度的量化方法,以及根据综合传导影响度识别优先修改单元的策略指导。
1 需求—产品的功能层解析
1.1 需求—功能映射表达
需求是产品开发及改进的驱动力,功能是产品的实质价值属性,用户需求(CRs)的满足归根结底为用户对产品期望功能的实现,因此需要建立用户需求与功能的映射机制,以用户需要的功能为产品实例的适应性修改目标,通过变换产品内部结构实现产品实际功能向用户期望功能的转变,最终满足用户功能需求。需求与功能的映射及表达步骤如下:
步骤1需求整理。结合亲和图[14]的分类思想,将获取的CRs细化整理为功能性需求FRs和非功能性需求NFRs两个需求集,其中FRs={FRi|i=1, 2, 3, …,n},FRi为用户的功能需求;NFRs={NFRj|j=1, 2, 3, …,n},NFRj为用户对除产品功能外的其他外部层期望,如外观、价格等。
步骤2功能提取表达。以FRs作为实例产品的修改驱动需求集,对FRs中的各功能需求元素进行功能提取,采用功能动词加作用目标的方式进行功能表达。
步骤3功能参数表达。功能本身是一个抽象的概念,为将用户功能需求与所获取的机械产品实际功能进行量化匹配,引入功能参数FP对步骤2中提取的功能进行参数量化表达。
1.2 产品功能域可拓集的构建
第1.1节构建了需求到功能的映射和参数表达,为确定产品实际功能对用户功能需求的满足度,实现产品功能域划分,需建立用户功能需求与实例产品功能的量化匹配机制,因此本节进一步以关联函数作为功能和需求的相关度量化工具,将关联函数值作为产品功能模块划分的依据,并以可拓集的形式表达功能域。
定义1设U为机械产品的功能论域,u为U中的任意元素,即功能提取表达中的Ft,称
Epro-func={(u,y)|u∈U,y=k(u)∈R}
(1)
为产品功能论域U上的一个功能域可拓集。
式(1)中y=k(u)为Epro-func的关联函数,其值为实域R中的元素,考虑到实际产品功能中的FP值与用户功能需求中的FP值一般是区间与区间、点与区间之间的匹配关系,本节采用初等关联函数和简单关联函数,限于篇幅,关联函数的详细构造可参见文献[15]。
对于定义1中的产品功能论域U,可按关联函数值大小将U分为弹性需求功能域、量变需求功能域、质变需求功能域3部分:
(1)弹性需求功能域(V++)
指能满足用户功能需求的那部分产品功能所组成的功能域,功能域区间为[1, +∞),单个功能元素u的关联函数值k(u)∈[1, +∞),具体表示为
V++(Case_Funt)={(u,y)|u∈U,y=
k(u)∈[1,+∞)}。
(2)量变需求功能域(V+)
产品实际功能与用户功能需求不能完全匹配,即存在功能偏差,将该部分功能组成量变功能域,功能域区间为[0, 1),单个功能元素u的关联函数值k(u)∈[0, 1),具体表示为
V+(Case_Funt)={(u,y)|u∈U,y=
k(u)∈[0,1)}。
(3)质变需求功能域(V-)
指在用户功能需求的要求下,产品本身所缺失的那部分功能组成的功能域,功能域区间为(-∞, 0),单个功能元素u的关联函数值k(u)∈(-∞, 0),具体表示为
V-(Case_Funt)={(u,y)|u∈U,y=
k(u)∈(-∞,0)}。
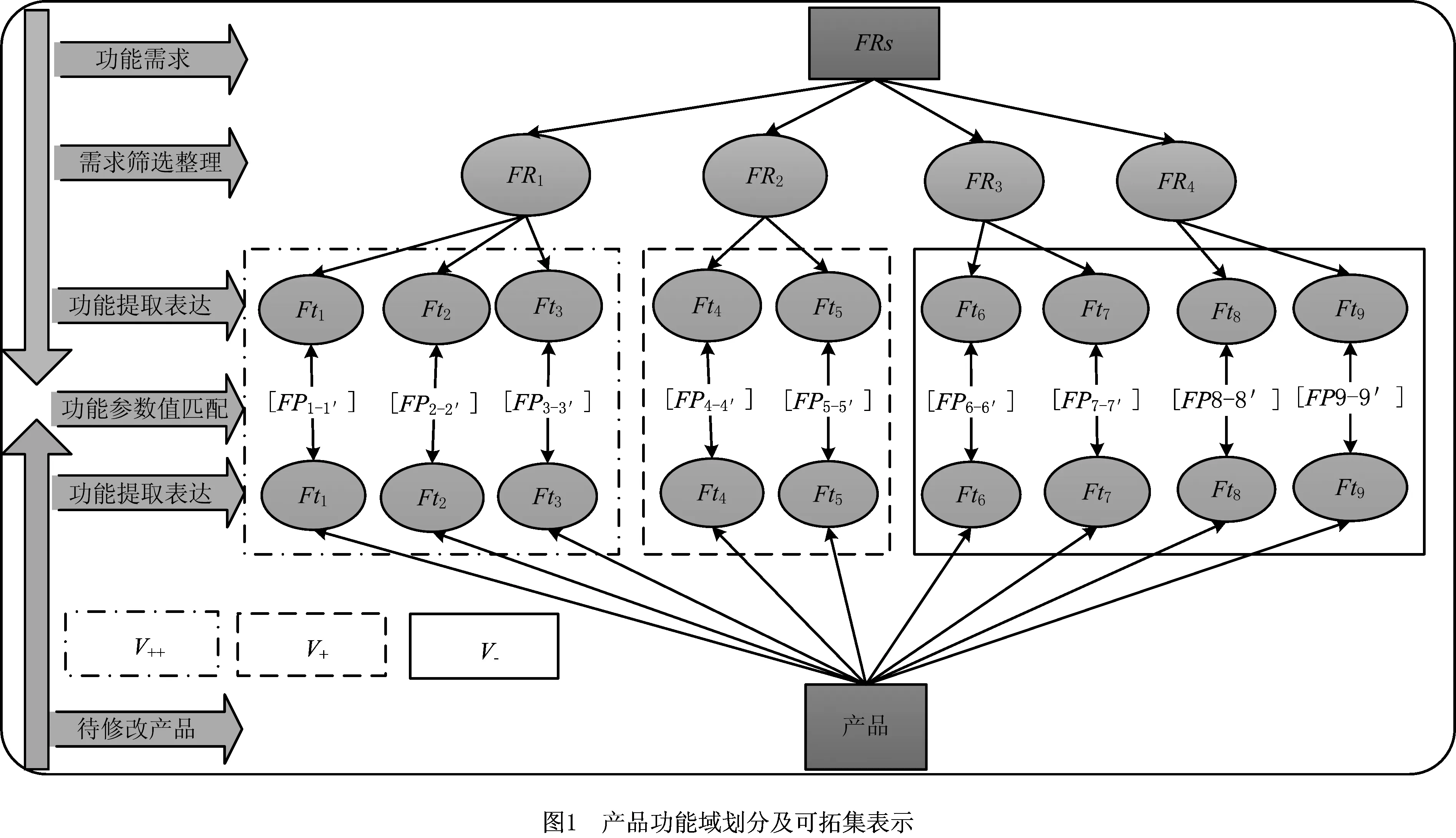
图1所示为对产品功能域划分的形式化建模表示,在功能需求层,通过筛选和评估得到有技术可行性的功能需求,即设计人员可在技术层上修改产品结构,以实现对产品功能强度的调节;在产品层,结合第1.1节功能提取表达中的功能,通过功能参数FP进行双向匹配操作,按满足度情况分为3个功能模块,即U中的3个域。
文献[16]提供了一种通过功能—行为—结构(Function-Behavior-Structure,FBS)迭代映射构建模块功构分解模型的思路,本文则通过上述功能域的划分及功能元素的确定,以功能独立、行为共存、结构独立作为产品纵向分解原则,通过FBS方法对产品进行功能—行为—结构的多层分解,以剖析确定功能域中各功能元素对应的产品具体单元,同时利用可拓设计知识表示方法[17]对产品在多层FBS分解后的各层元素进行定性和定量化表示,本节利用事元模型表示功能事元AF和行为事元AB,利用物元模型表示结构物元MS,并对其信息进行存储,以便后期设计重用时从计算机内部调取。对产品多层FBS纵向分解的数学描述模型为
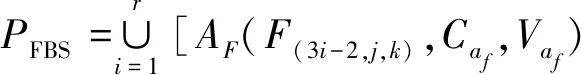
AB(B(3i-1,m,n),Cab,Vab)⟹MS(S(3i,h,l),Cms,Vms)]。
(2)
式中:3i-2,3i-1,3i分别为功能事元AF、行为事元AB、结构物元MS的层序号;j,m,h分别为AF,AB,MS对应层的节点序号;k,n,l分别为AF,AB,MS映射到下一层的子节点数;C表示基元特征,一般为基元属性;V表示特征量值;符号“⟹”表示映射操作。因此,产品多层FBS纵向分解可看作为多个FBS父、子模块的纵向迭代延伸。
2 产品零件修改粒度细化表达
针对实例产品进行FBS多层分解后得到的功能域中的零部件,结合其在适应性修改中的难易度及修改程度,将产品零件分为标准件、修改件、定制件3类,如表1所示。

表1 机械产品内部零件分类
零件是装配的最小元素,单个零件可看作几何特征的集合体,在实例产品的修改过程中,对零件修改设计的本质是对其几何特征的修改变换,现有的有关变更设计的文献大多以零件作为研究产品变更影响的最小单元,其不足之处在于研究零件之间的变更影响时忽略了零件自身特征变换引起的自传导影响,因此本文对上述3类零件进行粒度细化至特征层,以特征作为研究零件自传导与互传导的最小单元,按零件特征不同的功能表现细化为4类几何特征体:
(1)结构体特征(Stc) 将单个零件上某一实现特定功能的结构实体特征(如轴类零件)分解为不同的功能轴段,轴段功能面起配合、支撑等作用,轴肩起轴向定位作用。
(2)孔槽类特征(Hoc) 实体结构中存在很多类型的孔、槽类特征,如沉孔、盲孔、键槽、滑槽等,在模型表达中将孔槽作为虚拟实体,通过与其他特征求差运算得到所需的结构。对于阵列式的Hoc,可以只提取其中一个特征的信息作为母特征,以阵列标识符标记其阵列操作,从而简化模型表达。
(3)基体类特征(Bac) 一些基座体类零件的主要作用为承载和隔离保护,可将其作为一个整体基座特征,对于附属在基体上面的重要Stc及Hoc,可以单独分割。
(4)辅助类特征(Asc) 指实体结构中的一些倒圆、倒角、退刀槽、越程槽等通用的辅助功能特征,其加工尺寸可根据表约束选取。Asc在实体结构中广泛存在,3类零件中均有涉及,在后期图论化建模中,为简化模型可先隐藏该部分特征,待最终修改方案成型后再进行Asc重建。
文献[18]在对机械零件变型设计前期的知识建模中,提出一种零件特征的知识表达方法,即借助物元、关系元和事元分别表征零件几何特征体的信息、约束关系、拓扑变形操作。为实现零件修改粒度的模型化表达,本文以可拓物元(M)作为上述单个特征体的信息封装单元:

(3)
式中特征物元包括特征标识码(Identity_Featj)、形体尺寸信息(Size_Featj)、功能信息(Function_Featj)、属性特征信息(Attribute_Featj)等。
图2所示为上述零件类别、零件特征类别和相关属性特征的架构表示。
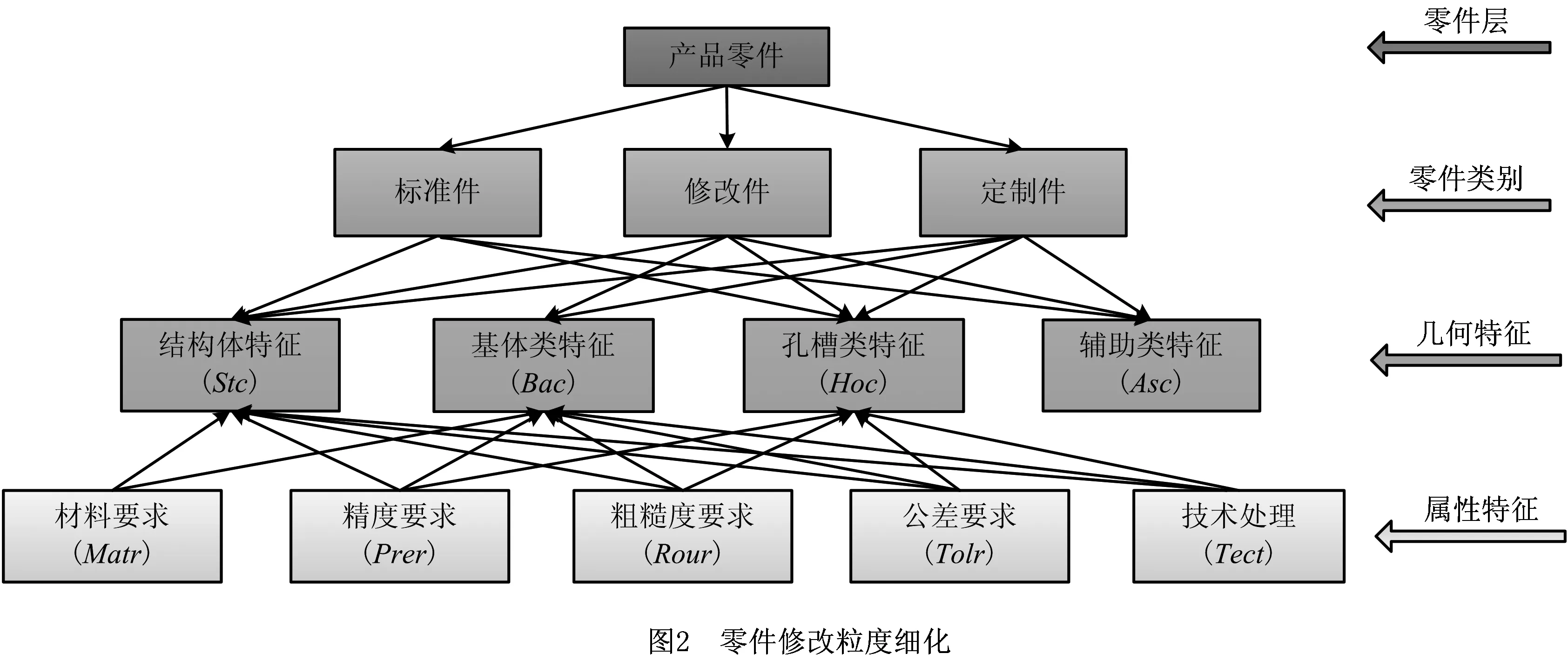
通过特征划分及特征模型构建,结合布尔运算,单个零件通过特征物元表示为
Parti=Mi-1*Mi-2*Mi-3*…*Mi-k。
(4)
式中:i为零件序号;M为实体特征的物元表示;符号“*”为布尔运算符,即∪(并)、∩(交)、(差)运算,视具体情况选用。
式(4)为产品单个零件的模型表达,实例产品通常为多个零件装配而成,零件间的装配可看作零件接口实体特征之间的配合,因此实例产品也可通过式(4)进行模型表达。
3 适应性修改单元识别
3.1 基元有向图的定义
利用图论的形式可有效表达产品内部功能、结构、知识、信息等要素,考虑传统图论中只表达了节点和节点间的简单关联关系,本文对其进行改进,提出基元有向图方法,实现了产品图论模型表达及信息挖掘。
定义2将基元有向图GE定义为一个三元组(M,R,O),记GE=(M,R,O)。其中:M为非空有限物元集合,M={Mi|i=1, 2, 3, …,n},M内部元素为第2章中构建的特征物元,将其作为GE的节点;R为非空有限关系集合,表示GE的边向量,其方向表示节点修改的效应传导方向,其内部元素表示节点间的关系,记作R={R1,R2, …,Rn};O为非空有限运算集,表示GE中属于同一零件的相邻节点间存在的布尔运算(并集、交集、差集运算),记作O={O1,O2,O3}。
定义3给定基元有向图GE=(M,R,O),M={Mi|i=1, 2, 3, …,n},对于∀Mi∈M,定义选取的某个变换特征节点Mi为主动传导元,当节点属于标准件时,一般不作主动变换,且在构建GE时可适当缩减,若∃Mj∈M,i≠j,Mi与Mj有直接或间接的相关关系,则定义Mj为从动传导元,当选择对象发生变化时,主动传导元与从动传导元会发生动态变化。
定义4给定基元有向图GE=(M,R,O),以主动传导元作为始节点向其他节点传导辐射,以单条关系边的节点作为终节点,始节点与终节点之间的单条路径链称为相关链。
定义5对于给定的基元有向图GE=(M,R,O),将GE中节点的边向量流入数量定义为该节点的流入度IND,边向量流出数量定义为该节点的流出度OUD。
3.2 基元相关矩阵的构建
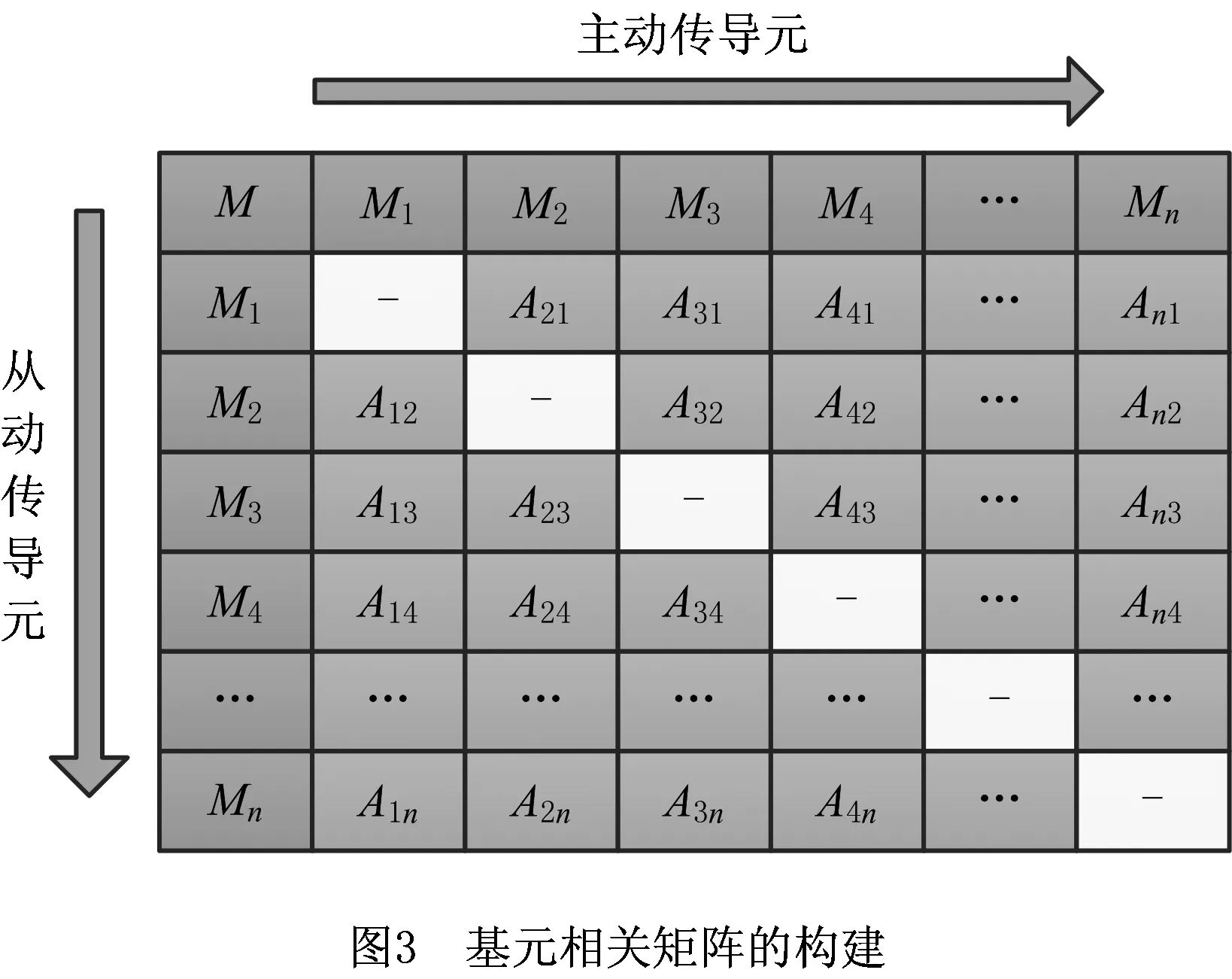
第3.1节中,构建GE可直观化表达产品零件自身及零件之间的关系与效应传导,为定量化表达和研究产品内部的相关性,本节进一步构建基元相关矩阵,如图3所示,其内部元素分为两类:
(1)特征物元(M)
提取基元有向图GE中的节点作为基元相关矩阵的第1行第1列元素,将基元相关矩阵第1行元素作为主动传导元,第1列元素作为从动传导元,主动传导元和从动传导元可提取和表达GE中相邻节点间关于评价特征EC的单向相关或双向相关关系。当主动传导元向与其相邻的节点进行修改效应传导时,可将接收到效应传导的从动传导元看作为一个新的主动传导元。
(2)关系子矩阵(Aij)
将GE中的R元素作为评价特征EC,实际中的R一般为多评价特征集,则主动传导元与从动传导元之间关于某一评价特征的相关关系可用数值表示(有相关关系为1,无相关关系为0),例如M1和M2之间的关系子矩阵为A12,存在3个评价特征(EC1,EC2,EC3),若M1和M2之间关于EC1和EC3相关,则A12=[1, 0, 1],将其记录于基元相关矩阵。
3.3 综合传导度的计算
基元相关矩阵可表示节点与节点间的关系类型及关系存在与否,对于单个节点的综合传导影响程度还缺乏计算表示,结合上述基元有向图GE和基元相关矩阵,引入节点变动因子NCF作为节点综合传导度量化指标,将NCF量化为流通指数Q、开源指数H、延伸指数S3个指标:
(1)流通指数Q将节点涉及的相关链条数定为流通指数Q,则定义节点Mi的流通指数Q(Mi),
(5)
式中l(Mi,Mj)表示始节点Mi与终节点Mj之间的相关链条数,两节点之间的相关链条数越多,传导路径越多,即Q值越大,变动影响越容易传导。
(2)开源指数H将与节点直接相连的节点数定为开源指数H,因为节点间以边向量相连,所以可利用流入度IND和流出度OUD表示开源指数H,即
H(Mi)=INDMi+OUDMi。
(6)
开源指数H反映了当前节点的初级传导范围,H值越大,初级传导的影响越大。
(3)延伸指数S将每条链中除节点自身外的其他节点数与该链节点总数比值之和作为延伸指数S,则定义节点Mi的延伸指数S(Mi):
(8)
式(7)为单条链中除节点Mi外的其他节点数与该链节点总数的比值,式中m(Mi,Mj)表示始节点Mi与终节点Mj之间任一相关链的节点总数,S值越大,对当前节点变换引起的效应传导波及范围越大。
将流通指数Q、开源指数H、延伸指数S进行归一化处理后求和,并定义节点变动因子NCF如下:
式中:P(Mi)为节点Mi的变换概率,W(Mi)为节点Mi的邻接相关概率,
P(Mi)=Ppart×Pstru,
(10)
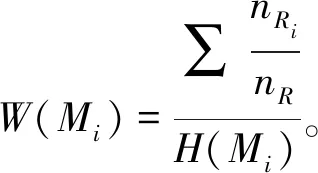
(11)
式中:Ppart为零件变换概率,Pstru为特征变换概率,结合实际变动情况,Ppart和Pstru的概率取值如表2和表3所示;nRi为Mi与其相邻每一节点的关系数目,即基元相关矩阵中以Mi为主动传导元时,Mi与其直接相关的从动传导元之间的关系子矩阵Aij中量值为1的关系数目,nR为GE中R内部元素的个数,即基元相关矩阵中单个关系子矩阵Aij的列数。

表2 零件变换概率值

表3 特征变换概率值
因为辅助类特征在GE中不具体体现,所以表3中只包含其他3种特征的变换概率值。将属于同一零件的各特征节点的NCF值求和,得到该零件的变动因子PCF,即零件的综合传导度
PCF(Pi)=∑NCF(Mi)。
(12)
通过上述方法处理,将产品中各个零件的变动因子大小进行排序,PCF值越大,对应的零件综合传导影响度越大,因此对于多层FBS纵向分解得到的属于各功能域中的零件,设计人员制定修改方案时以零件PCF值作为参考,PCF值较大的零件可作为修改警示单元,为提高修改效率,减少修改成本,应尽量避免修改或少修改这些单元。具体制定修改策略时,以满足PCF值较小、功能域属于V+或V-、功能贡献度较大的零件作为优先修改单元(功能贡献度等于单个零件的物元特征节点数与目标功能映射下的所有零件特征物元节点数的比值),在此基础上进一步参考该零件的NCF值,优先修改该零件中NCF值较小的特征。通过上述方法,设计人员可以方便地制定出对产品整体变动更小的修改方案,从而节约修改设计的时间和成本。
4 实例验证
本文以一款某型号螺蛳切尾机设备的改进设计为例对所提方法进行验证。首先对用户需求进行收集,得到CRs={01-价格便宜; 02-操作简单; 03-携带方便; 04-能够自动卸料; 05-能够收集剪切完的废料; 06-剪切效率比较高},结合亲和图分类思想,由设计人员分析后汇总得到功能性需求FRs={FR1=〈能够自动卸料〉;FR2=〈能够收集剪切完的废料〉;FR3=〈剪切效率比较高〉}和非功能性需求NFRs={NFR1=〈价格便宜〉;NFR2=〈操作简单〉;NFR3=〈携带方便〉}。
对筛选得到的FRs进行功能提取表达及功能参数表达,得到FRs={FR1=〈Ft1-卸运螺蛳,FP1-1-卸料率,FP1-2-人工参与度〉;FR2=〈Ft2-收集废料,FP2-收集率〉;FR3=〈Ft3-剪切螺尾,FP3-剪切率〉}。
结合案例实际,参照文献[15]中左、右侧距计算公式,以及最优点在x0处达到时的初等关联函数构造情况,计算关联函数值。对上述功能参数FP的用户理想域X0、扩展域X、最优点x0、设备实际能达到的功效值x,以及FP按关联函数公式进行计算得到关联函数值,如表4所示。
由表4计算所得的关联函数值可知k(FP2)∈(-∞, 0),k(FP1-1),k(FP1-2)∈[0, 1),k(FP3)∈[1, +∞),则结合功能域可以得到Ft2∈V-,Ft1∈V+,Ft3∈V++。
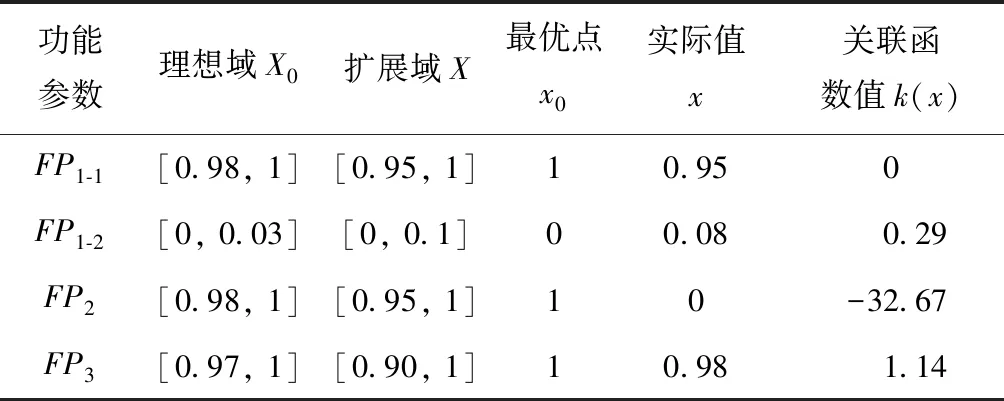
表4 功能参数关联函数值计算
以Ft1,Ft2,Ft3作为多层FBS纵向分解的初始分解功能项(如图4),对本产品案例实施多层FBS纵向分解得到零件:01-滚筒,02-支杆,03-低速轴,04-大齿轮,05-小齿轮,06-低速轴轴承,07-高速轴,08-高速轴轴承,09-支架,10-刀片,11-联轴器,12-电机,13-外壳,14-进料漏斗,15-出料槽。对上述零件进行外设、动力源、部分标准件约减,得到产品功能主体装配零件,即零件序号为01,02,03,04,05,07,09,10,对应的零件物元模型分别为M1,M2,M3,M4,M5,M7,M9,M10。
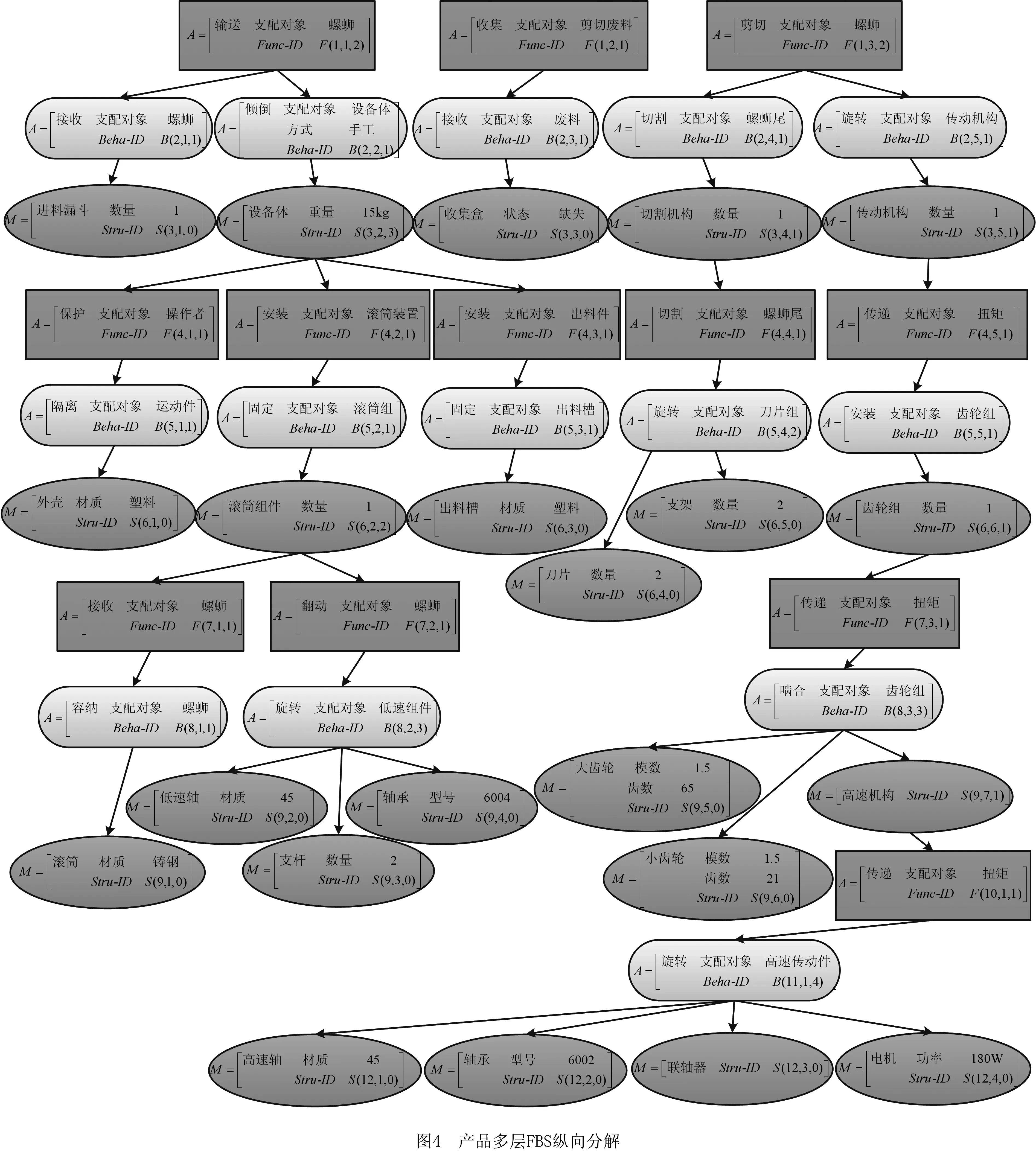
各零件特征物元为:M1={M1-1(滚筒外腔体),M1-2(圆锥孔),M1-3(滚筒内腔),M1-4(支杆孔),M1-5(端面封片)};M2={M2-1(支杆)};M3={M3-1(轴承段),M3-2(中间段),M3-3(轴承段),M3-4(齿轮段)};M4={M4-1(大齿轮齿体),M4-2(大齿轮安装孔)};M5={M5-1(小齿轮齿体),M5-2(小齿轮安装孔)};M7={M7-1(联接段),M7-2(齿轮段),M7-3(轴承段),M7-4(中间段),M7-5(轴承段)};M9={M9-1(支架杆)};M10={M10-1(刀片体)}。
结合上述零件物元特征及第3.1节的GE构建方法,对上述功能主体装配零件构建GE,如图5所示。
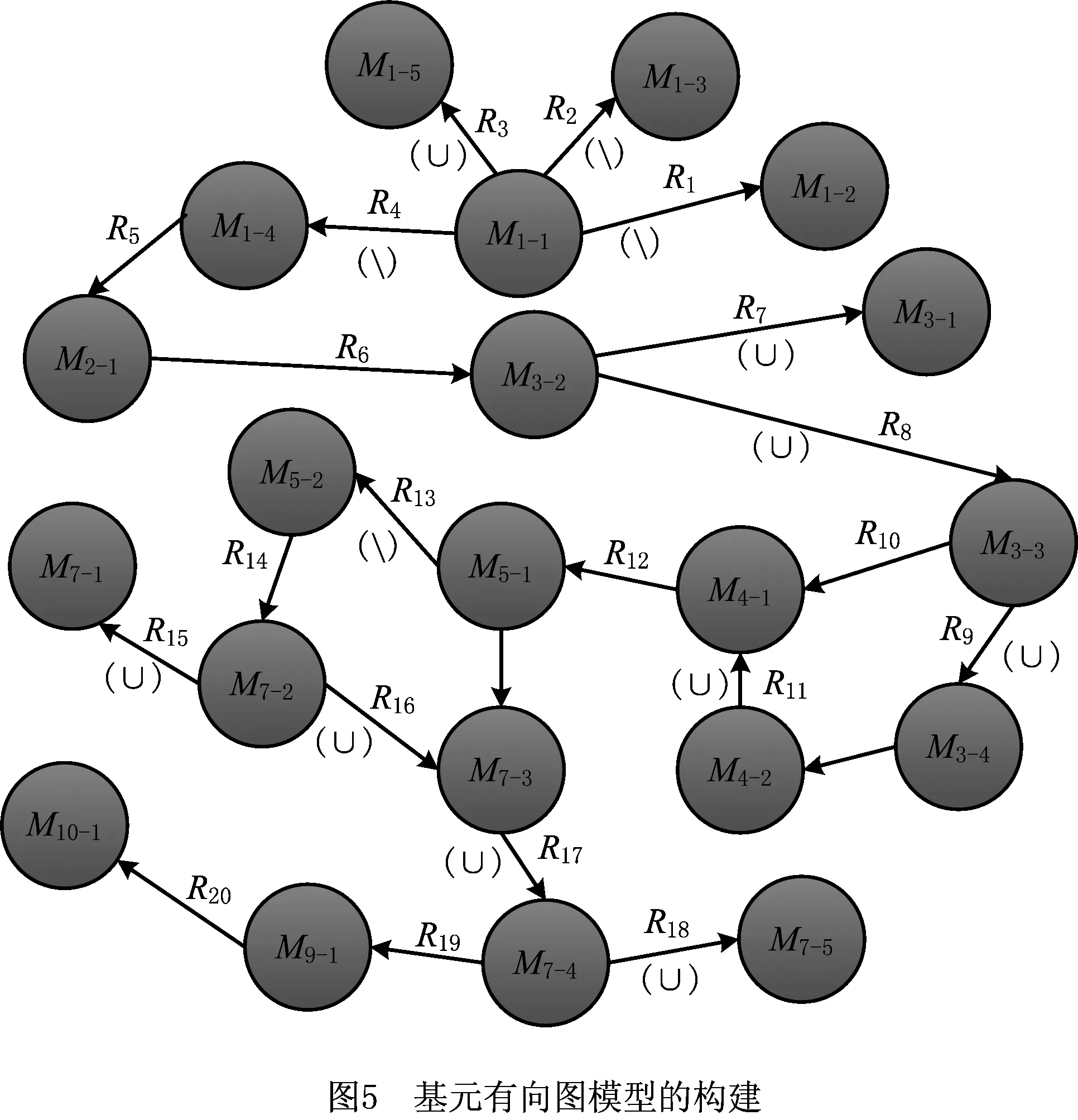
提取图5中的各物元节点,构建关系集合R={01-尺寸关系; 02-配合关系; 03-位置关系; 04-偏置关系; 05-布尔关系; 06-连接关系},将图5各节点之间的关系量值记录于基元相关矩阵,如图6所示。
通过构建GE和图6的基元相关矩阵,并结合第3.3节各式计算NCF量化指标值和NCF值,如表5所示。

表5 节点各指标计算值
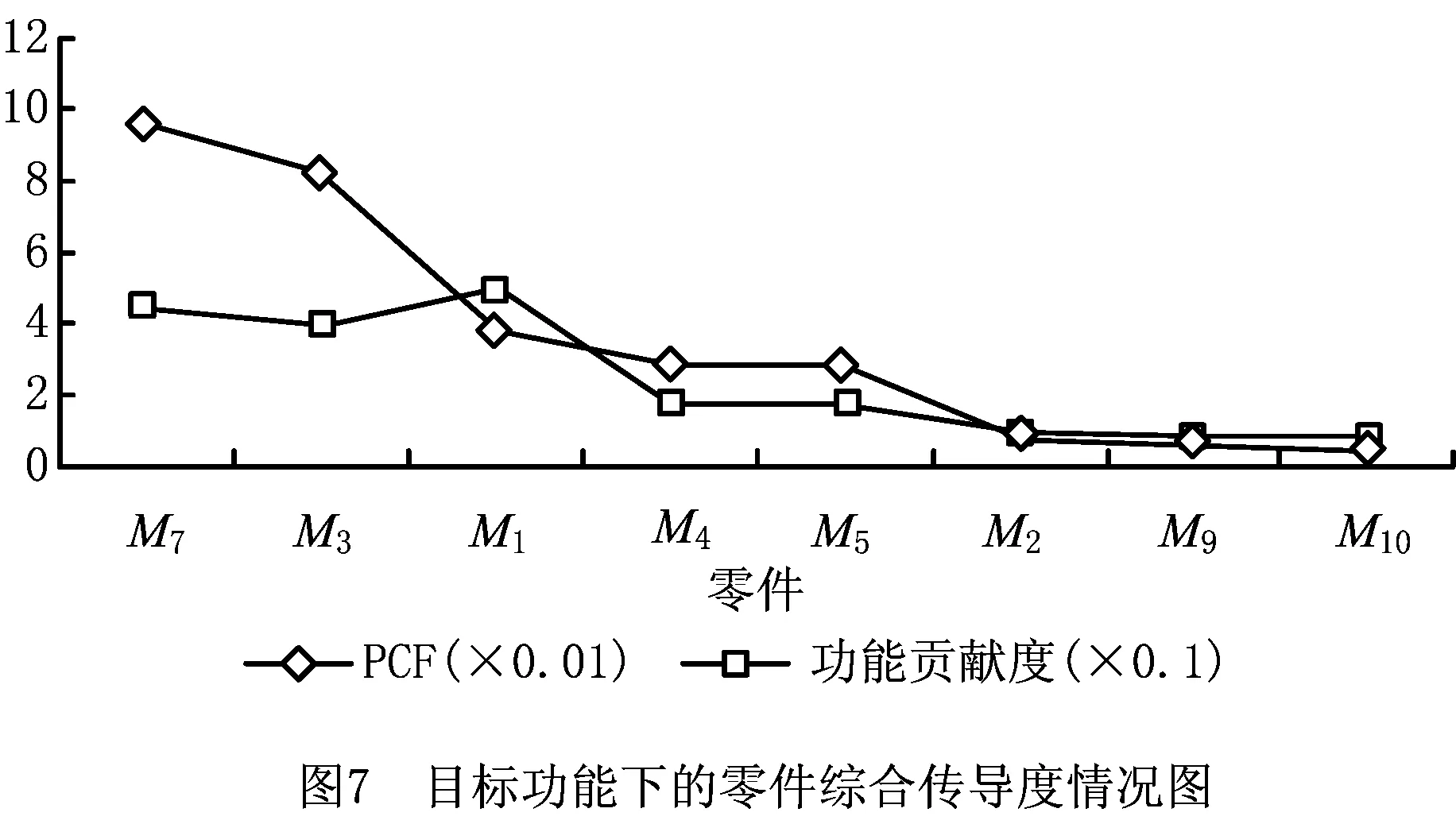
结合表5数据和式(12),同时考虑零件对目标功能的贡献度,得到单个零件的PCF值排序曲线图,如图7所示。
分析图7可见,M7和M3的PCF值较大,修改引起的传导影响较大,当设计人员制定修改方案时,应尽量避开零件M7和M3;零件M4,M5为一对啮合齿轮组,PCF值较小,但其功能—结构映射属于V++,即属于满足功能需求的域区间,不作为首选修改单元;零件M2,M9,M10的PCF值均较小,但其均为单一特征体,功能结构简单,对功能贡献较小,不作为优先修改单元;对比零件M1,其PCF值相对较小,其功能—结构映射属于V+,是功能有偏差的域,且零件特征数占比大,对功能贡献度多,因此选取M1零件作为优先修改单元,进一步结合M1各特征物元的NCF值,取NCF值较小的M1-2和M1-3作为优先修改特征,其次取M1-5,最后取M1-1。结合相关设计人员修改意见,以M1修改实施为例,为M1-3添加螺旋叶片,将M1-2的排布方式变换为螺线式排布,删除M1-5,对M1-1的另一端面增加半圆挡片,从而完成M1的修改设计,如图8所示。

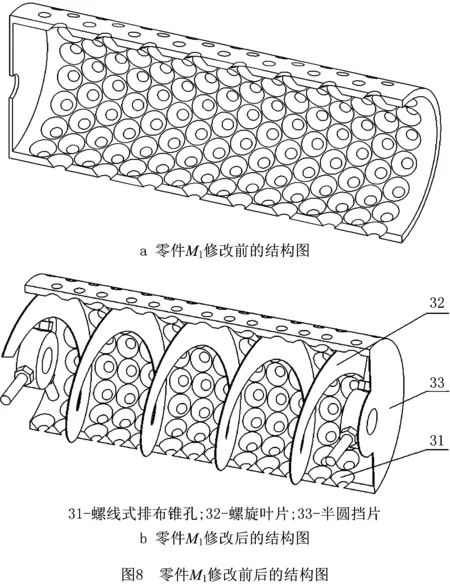
与原结构相比,修改设计后的滚筒腔体右端部的半圆挡片能够进行间歇式自动进料,防止螺蛳一次性倒入时堆积在滚筒腔右端,螺线式排布锥孔和螺旋叶片配合能够对螺蛳边剪切边自动输送,最后从滚筒腔体左端输出成品,改变了原设备剪切完螺尾后需人工卸料的工作方式。改进后的设备减少了人工参与度,而且能够连续剪切和输送,提高了工作效率。
该方案进一步完善后已获得专利“螺蛳切尾机(CN201710227343.5)”。
5 结束语
本文针对功能需求驱动下的产品适应性修改单元的识别问题,提出一种修改单元识别方法。建立了客户功能需求与实例产品功能之间的量化匹配模型,通过多层FBS实现产品实例纵向分解,明确了产品的适应性修改功能域、功能元素、功能—结构实体映射。引入基元理论作为产品内部单元信息记录及表达工具,通过零件的特征划分及物元建模细化了产品修改粒度,深化了对产品内部单元修改效应传导的分析研究。在产品修改粒度细化的基础上进一步构建基元有向图,实现了产品的图论化表示,并以图论模型作为信息提取源计算基元有向图中特征物元节点的NCF值及零件的PCF值,最终获取优先修改单元,为设计人员制定产品修改方案提供了理论参考。
本文后续工作包括挖掘零件自身特征之间及不同零件相互之间的关联关系,构建相关性函数及修改效应传导机制,实现修改效应的动态量化表达,同时借助计算机并结合可拓变换方法实现待修改单元的智能化适应性修改,以提高产品修改效率,减小产品修改成本。

