基于改进CA模型的群体辟谣信息扩散效果预测

滕 婕，夏志杰，占 欣

上海工程技术大学 管理学院，上海201620

1 引言

公共危机事件发生后，人们对于信息的渴求异于平常，谣言在短时间内快速扩散，往往比事件本身的影响更大，更易造成恐慌和混乱局面，影响社会安定[1]，及时、有效地进行信息辟谣是消减危机事件影响的有效措施[2]。为了提升辟谣信息扩散效果，已有研究从信源可信度[3]和信息发布内容[4-6]的角度给出了增强信息传播效果的途径。但实际上，信息是一个通过个体之间的局部信息交互，形成群体复杂信息行为的复杂过程[7]。公共危机情境下，群体之间的信息协同对有效解决危机事件信息缺乏或过载等问题具有较好的作用[8]。因此，从微观角度了解辟谣信息在群体之间传播的影响因素、规律，对辟谣信息扩散效果的预测和信息协同效率的提高都具有重要意义。

本研究采用改进的元胞自动机（Cellular Automata，CA）来研究辟谣信息的传播。首先，借鉴SEIR 传染病模型，对有限群体成员的信息状态进行划分。其次，在传统元胞自动机上加入个体异质性的元素，建立异质元胞自动机的辟谣信息扩散模型，研究辟谣信息扩散的影响要素、过程及传播规律，以期为辟谣信息传播的定量化分析和信息传播趋势的有效预测提供理论与方法支持。

2 基于SEIR模型的信息主体的状态划分

辟谣信息是出现在谣言之后，所以在辟谣信息出现之前，谣言已经在群体间进行了大范围传播[9]。公众通过相互之间的互动进行信息的扩散，信息的扩散和传染病的不断传染具有本质上的一致性[10]。谣言和辟谣信息相对产生，都属于信息扩散的范围，尤其在公共危机事件下，两者的传播具有较多的相似处，它们有着一致的扩散过程，并且都是通过节点连接以一定概率影响节点状态改变达到传播的目的。

根据谣言传播过程的分析，个体的交流策略、信息状态和分布类型处于不断变化之中。本研究将辟谣信息扩散中拥有不同程度信息获取状态的信息个体划分为4 个类别：无知者（S 态，指从未接触任何谣言和相关的辟谣信息，但已具备获取信息的渠道和能力）、谣言接触者（E 态，指已对谣言进行浏览和仔细阅读，还未做决定是否进行传播）、谣言传播者（I1态，指经过综合考虑，决定对谣言执行传播行为的个体）、辟谣信息传播者（I2态，主动辟谣的官方权威机构或接触官方辟谣信息的个体，对辟谣信息执行传播行为）。

3 公共危机事件下辟谣信息扩散的异质元胞自动机模型

考虑到元胞个体在信息获取能力、传播能力等方面存在较大的差异，因此本研究从公众接收信息的微观层面，提出一个描述信息传播过程的异质元胞自动机模型。设C 为n×n 的二维元胞空间，C(i,j)表示二维元胞空间中任意一元胞。由于个体对信息的获取程度与信息源的关系强度有关，人际关系的远近程度直接影响个体间信息的获取程度[11]，所以本研究将二维元胞空间中的任意元胞C(i,j)与元胞C(p,q)的距离定义为关系强度距离，元胞距离越近意味着信息的获取程度越大。

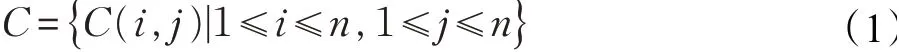
其中，i,j,p,q是C(i,j)在二维元胞空间中的坐标值。

3.1 模型的基本假设

确认不同因素对个体的影响方式和影响程度是本研究的重点和难点，为了便于研究，作出以下假设：

（1）群体规模是固定的，群体中新进入的个体以概率b成为无知者，无知者、谣言接触者、谣言传播者、辟谣信息传播者分别以概率b1c(i,j)、r2c(i,j)、r1c(i,j)和oc(i,j)移出传播网络，概率均服从（0，1）的正态分布，但成员总数量固定，即，b=b1c(i,j)+r2c(i,j)+r1c(i,j)+oc(i,j)。由于个体异质性，针对公共危机事件发布的特定主题下的谣言和辟谣信息，不同信息接收状态的个体间转化概率不一样，同种信息状态的个体也具有不同的信息接受能力和传播能力。

（2）无知者（S）通过与谣言传播者进行信息交流，分别以不同大小概率P1c(i,j)转变为谣言接触者（E）和谣言传播者（I1）。

（3）谣言接触者（E）受到周围环境的影响，以概率Ic(i,j)成为谣言传播者（I1）；同时，由于谣言接触者受到辟谣信息传播者的影响，谣言接触者（E）也会以概率Rc(i,j)成为辟谣信息传播者（I2）。

（4）谣言传播者（I1）收到官方辟谣信息的影响，以不同概率P2c(i,j)成为辟谣信息传播者（I2）。

3.2 平衡点及其稳定性

公共危机事件下辟谣信息扩散中，不同信息接收状态的个体相互转化的过程如图1所示。

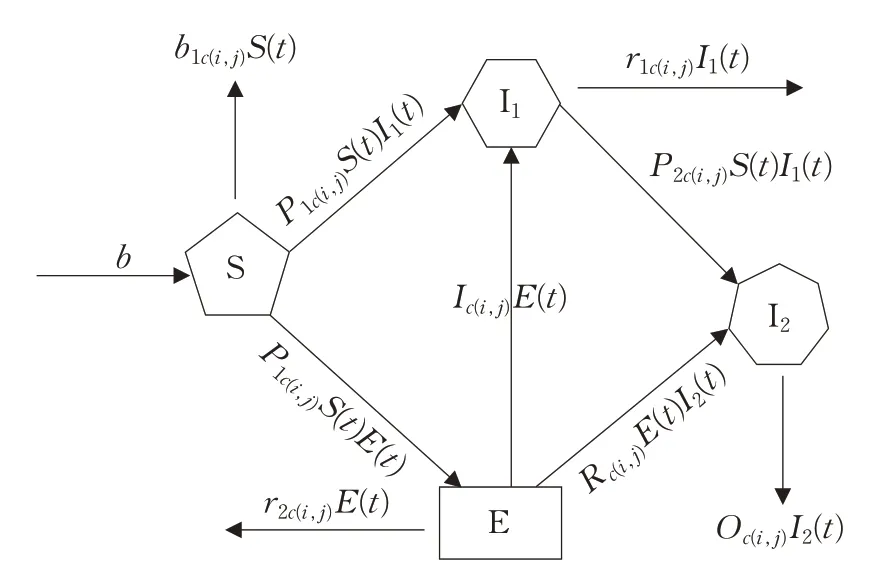
图1 辟谣信息发布后不同状态个体间的转化

以往研究对SEIR 模型中各个参数为固定值产生了质疑，并提出了动态改变参数的观点[12-13]，本研究基于传染病模型，引入了辟谣信息发布节点，讨论了辟谣信息发布节点对抑制虚假信息传播的显著影响作用。根据图1 不同状态个体间的转化过程可以得出微分动力方程组模型（4）。其次，针对个体异质性对信息传播影响的问题，不同状态个体间转化的概率由二维元胞空间中 的 元 胞 个 体 C(i,j)决 定 ，其 中 ，C={C(i,j)|1 ≤i ≤n,1 ≤j ≤n},i,j 是C(i,j)在 二 维 元 胞 空 间中的坐标值。

借鉴传播学中基本再生数R0的定义，辟谣信息传播模型的基本再生数为单个辟谣信息传播者在其传播周期内所影响的无知者的个数[14]。基于微分方程组，给出R0附近超阈值和亚阈值谣言传播平衡点存在性和稳定性的一个简单判据[15]。

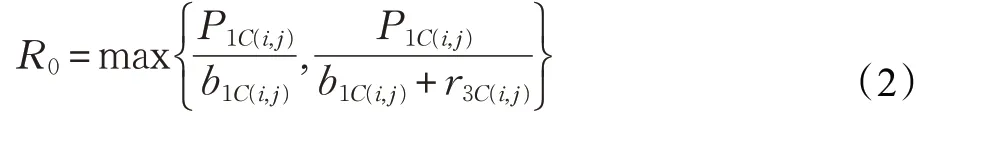
因为信息的传播过程中，参与群体讨论的总体数量是固定的，所以微分方程式需满足以下：

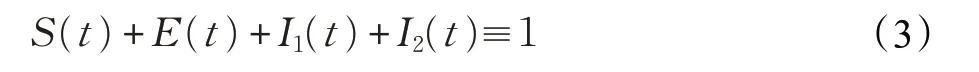
其 中 各 状 态 个 体 的 比 例 集 合 为 ：A={(S,I1,I2):S ≥0,I1≥0,I2≥0,S+I1+I2≤1}，辟谣 信息扩散过程的平衡点如下：

当R0＜1 时，微分方程组存在最开始的平衡点K0=(S,I1,I2)=(1,0,0)，当R0＞1时，微分方程组存在平衡点K1、K2、K3和K4，其值分别为：

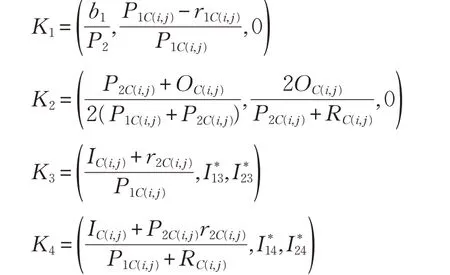
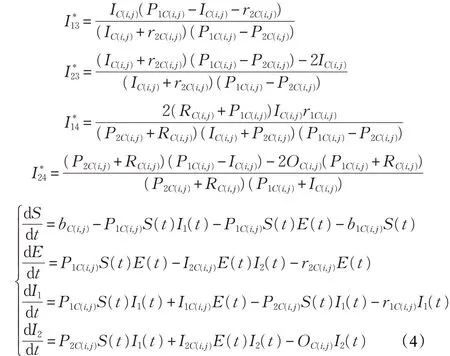
3.3 辟谣信息扩散的异质元胞自动机模型

由于二维元胞空间中，元胞个体处于4 种不同的信息接收状态，C′C(i,j)表示元胞状态集，C′C(i,j)={0 ,1 ,2,3} 代表4 个状态，即4 个不同的元素对应元胞t 时刻的状态：C′C(i,j)=0表示无知者（S）；C′C(i,j)=1表示谣言接触者（E）；C′C(i,j)=2表示谣言传播者（I1）；C′C(i,j)=3表示辟谣信息传播者（I2）。

元胞邻域体现元胞之间信息传递时邻居元胞的分布形式，典型的元胞邻域为VonNeumann 邻域和Moore邻域，如图2 所示。其中黑方格为研究的中心元胞，白格为邻居元胞。

公共危机事件下，无知者和谣言传播者的信息的传递分别取决于信息获取概率P1C(i,j)×C(p,q)和P2C(i,j)×C(p,q)，dC(i,j)×C(p,q)表示任意两个元胞之间的距离，即

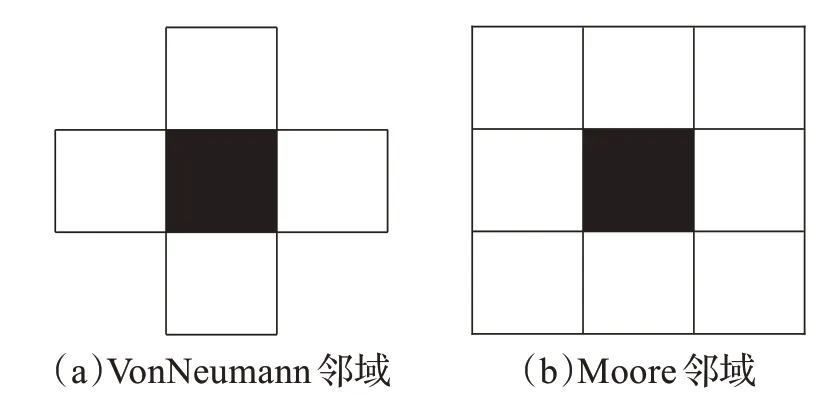
图2 典型标准邻域

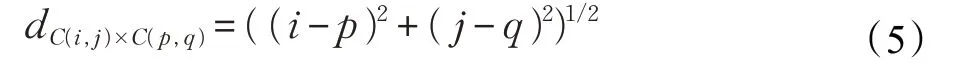
信息获取概率是由学习能力、传播能力和元胞距离综合决定，无知者的学习能力、谣言传播者的学习能力、谣言传播者的传播能力、辟谣信息传播者的传播能力和元胞距离分别为f1C(i,j)、f2C(i,j)、g1C(p,q)、g2C(p,q)、dC(i,j)×C(p,q),且f1C(i,j)、f2C(i,j)、g1C(p,q)和g2C(p,q)均服从（0，1）正态分布，以此来描述元胞个体具有差异性。即：

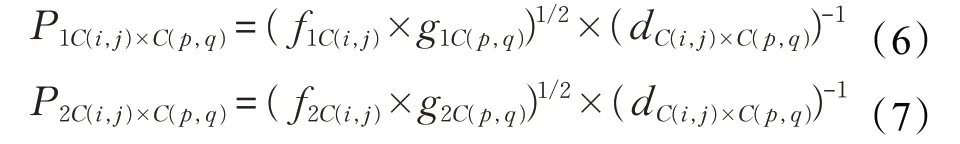
元胞个体的信息获取概率与自我学习能力、传播者的传播能力成正比，与元胞距离成反比，即PC(i,j)×C(p,q)的值是由fC(i,j)、gC(p,q)和dC(i,j)×C(p,q)确定。

由于信息获取概率PC(i,j)×C(p,q)会受到邻居元胞中信息传播者的传播能力影响，公共危机事件中，惶恐和焦虑情绪往往会刺激人们探索真实的信息，寻求信息传播能力最强的元胞个体进行交流。以往研究把传播能力的大小作为判断意见领袖的方法[16-19]。季丹等提出网络意见领袖对危机信息传播发挥着巨大的作用[20]。陈福集等通过研究发现，在突发事件发生时，意见领袖在信息传播中不仅能起到增强信息传播的作用，还可以引导舆论的发展方向[21]。越来越多的研究表明，意见领袖在信息传播扩散、网络舆情监控、网络口碑效应等社会现象中具有不可估量的作用[22-23]。所以，当公众寻求周围传播能力强的个体获取信息时，本研究将这种获取信息的方式称为意见领袖寻求策略。在该策略下，信息获取概率为：

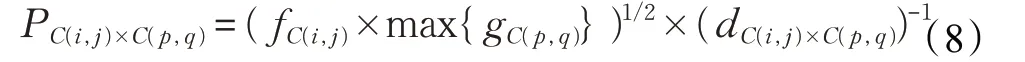
信息获取概率还与元胞间的关系强度有关。郑琼等通过对社交互动行为的特征提取研究发现，社交的关系强度影响用户的信任度[24]。公共危机事件下，人们获取信息会受到与自己关系较好的人影响，和自己关系越紧密，关系强度越大，自己就会越相信对方，这种寻求与自己关系强度较高的元胞个体交流的方法称为关系强度策略。此时，信息获取概率为：

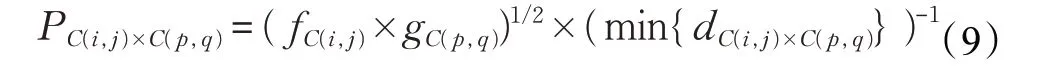
综合策略是在综合考虑邻居元胞传播能力和元胞关系强度下的信息交流方式，此时，信息获取概率为：

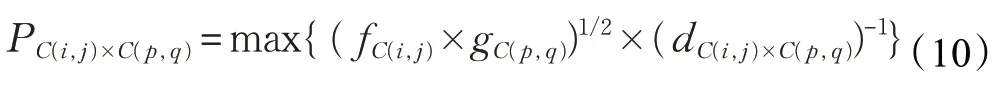
官方发布辟谣信息后，由于谣言传播者会受到辟谣信息传播者的强烈影响，谣言受到官方辟谣者的抑制，谣言传播者的传播能力会随时间而降低，即：

公共危机事件发生后，谣言接触者受到辟谣信息影响，其状态可能发生转化，转化可能性的大小分别由谣言传播率IC(i,j)、谣言免疫率RC(i,j)决定，二者均服从（0，1）的正态分布。

公共危机事件下，群体通过交互传递信息，部分非无知状态的个体接触辟谣信息后通过评论或通过带有评论的转发信息，不同类别的群体数量会随着辟谣信息的发布、传播发生改变，从而对网络结构产生一定的影响，因此，本研究将不同信息接收状态的个体之间发生转化的规则进行如下的定义：

（1）当元胞个体的状态为无知者（S），即S′C(i,j)=0，计算概率P1C(i,j)×C(p,q)，判断辟谣信息无知者的状态S′C(i,j)是否从0 变为1，即是否以P1C(i,j)×C(p,q)转变为谣言接触者，若不满足，进行下步判断，即，判断无知者的状态S′C(i,j)是否从0 变为2，即是否以P1C(i,j)×C(p,q)转变为谣言传播者，否则以概率b1C(i,j)移出信息协同群体。

（2）当元胞个体的状态为辟谣信息接触者（E），即S′C(i,j)=1，此时应判断谣言接触者是否以谣言传播率IC(i,j)概率转化为谣言传播者，即判断是否成立S′t+1C(i,j)=2，若不满足，进行下步判断，即，判断辟谣信息接触者是否以概率RC(i,j)转化为辟谣信息传播者，即判断是否成立S′t+1C(i,j)=3，否则以概率r2C(i,j)移出信息协同群体。

（3）当元胞个体的状态为谣言传播者（I1），即S′C(i,j)=2,此时应判断其是否以概率P2C(i,j)×C(p,q)转化为辟谣信息传播者，即判断是否成立S′C(i,j)=3，否则以概率r1C(i,j)移出信息协同群体。

（4）当元胞个体的状态为辟谣信息传播者（I2）即S′C(i,j)=2，此元胞会以Oc(i,j)移出信息协同群体。

4 仿真结果与分析

基于本研究提出的辟谣信息扩散模型，研究群体信息交互策略、辟谣信息传播者的分布模式、辟谣信息移出率对辟谣信息扩散的影响。设二维元胞空间用15×15正方形网格表示。在辟谣信息扩散的初始时刻，只存在谣言传播者、辟谣信息传播者、无知者三种状态的元胞个体；辟谣信息交互策略包含意见领袖寻求策略、关系强度策略和综合策略；辟谣信息传播者分布模式包括随机型、均匀型和垄断型；通过传播者比例it和速度vt量化辟谣信息传播效果，即：

仿真时长T=50。每种交互策略、辟谣信息移出率和分布模式对辟谣信息扩散影响效果仿真50 次，计算平均值作为其结果。

4.1 公共危机事件中不同信息交互策略下辟谣信息扩散效果

设辟谣信息交互策略分别为：意见领袖寻求策略、关系强度策略和综合策略，t=0 时刻，辟谣信息传播者为0.02，谣言传播者为0.20，信息无知者为0.78，二维元胞中元胞的分布模式定为均匀型分布，元胞邻域定为Moore 邻域。群体信息交互策略对辟谣信息的影响如图3 所示。有限群体内辟谣信息传播者的比例随时间推移，整体呈现递增趋势，辟谣信息传播速度经历了一个先增至峰值又递减的过程，其中峰值出现在辟谣信息扩散至整个二维元胞空间之后的若干时间步中，设此刻时间t=t0，辟谣信息传播者的数量在动态变化中上升至峰值，随后增加的数量随二维空间中其他元胞个体的状态的改变逐渐下降，辟谣信息的传播速度也减慢。在辟谣信息传播的后期，辟谣信息传播者比例逐步达到稳定状态，这种稳定状态会一直保持下去。

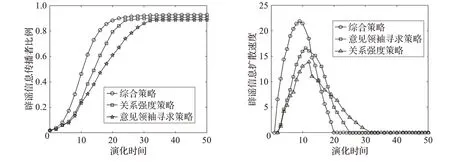
图3 信息交互策略下的辟谣信息扩散效果

从图3 中还可以看出，三种交互策略影响下的辟谣信息传播者比例趋势图中，一直处于最上方的线条是综合策略的交互方式。综合策略的辟谣信息传播效果明显高于关系强度策略和意见领袖寻求策略，因此综合策略的传播效果影响力最大。在辟谣信息传播初期，关系强度策略和意见领袖寻求策略的传播效果并没有明显的差异，意见领袖寻求策略和关系强度策略下的辟谣信息传播速度也很相近。在中后期的传播中，随着辟谣信息扩散范围的增大，意见领袖寻求者策略的影响力逐渐高于关系强度策略。这说明，与群体间交流所借助的人际关系策略远近相比，个体的传播能力的强度更能决定信息的传播效果，即人们的观点还是会更大程度上受到所接触到的意见领袖的影响。

4.2 公共危机事件中不同辟谣信息移出率下信息扩散效果

设群体间交互的辟谣信息移出率OC(i,j)分别服从（0，0.25）、（0.25，0.50）、（0.50，0.75）和（0.75，1.00）上的正态分布，t=0时刻，辟谣信息传播者为0.02，谣言传播者为0.20，信息无知者为0.78，群体信息交互策略为综合策略，二维元胞中元胞的分布模式定为均匀型分布，元胞邻域定为Moore 邻域。群体成员的移出率对辟谣信息产生的影响如图4所示。

元胞个体的辟谣信息移出率对辟谣信息扩散效果具有显著的负相关影响。具体地，公共危机事件下，信息移出率越高，最终的辟谣信息传播者比例越低，其辟谣信息传播速度也越慢。这是因为信息的移出率越高，表明公众接触到发布的辟谣信息时，未进行信息的传播，倾向于选择放弃对事件的传播，以较低的概率转变为辟谣信息传播者。

4.3 公共危机事件传播者不同分布模式下辟谣信息扩散效果

设初始辟谣信息传播者分布类型分别为垄断型、随机型和均匀型，垄断型指的是辟谣信息发布者的类型仅限于政府、地方政府及官方媒体，每一个类型构成一个信息发布群体。随机型是考虑到每个个体都可能在网络上对辟谣信息进行传播，辟谣信息传播者初始分布是均匀型。均匀型是指公共危机事件下，辟谣信息传播者在二维元胞空间中是等距存在的，即，群体结构中辟谣信息传播者之间的距离是一样的。t=0时刻，辟谣信息传播者为0.02，谣言传播者为0.20，信息无知者为0.78，信息交互策略为综合策略，元胞邻域为Moore邻域。初始辟谣信息传播者分布类型对辟谣信息扩散的影响如图5所示。

有限群体内辟谣信息传播者的比例随时间推移，整体呈现递增趋势，辟谣信息传播速度经历了一个先增至峰值又递减的过程。在辟谣信息传播的后期，辟谣信息传播者比例逐步达到稳定状态，需要指出的是，初始辟谣信息传播者呈集群型分布，辟谣信息传播者的比例最低，均匀型分布下的辟谣信息传播者的比例最高，随机型分布下的辟谣信息传播者的最终比例介于两者之间。均匀型分布使元胞个体较容易接触辟谣信息，不易被网络上谣言所误导。相反，若将辟谣信息局限在官方媒体中，这限制了辟谣信息传播者的传播能力以及其他状态的个体接触获取辟谣信息的可能性，从而使得集群式分布不利于辟谣信息的扩散。

5 结果与讨论

图4 群体辟谣信息移出率下的辟谣信息扩散效果

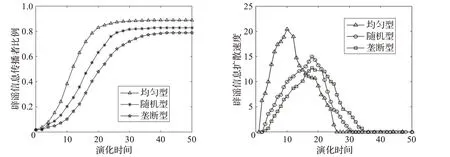
图5 辟谣信息不同分布模式下的辟谣信息扩散效果

本研究利用SEIR 传染病模型对有限群体内不同状态的元胞个体进行划分，根据群体成员的异质性建立辟谣信息扩散模型，从群体信息协同角度研究辟谣信息传播的过程及规律。实验中，设置仿真时长T=50，每种交互策略、辟谣信息移出率和分布模式仿真50 次，计算仿真结果的最优、平均值、最差值和标准差，平均值显示出寻优精度，标准方差反映了模型的稳定性，辟谣信息传播者比例变化和辟谣信息扩散速度实验结果如表1 和表2所示。

根据表1与表2的结果显示，首先，公共危机事件下辟谣信息交互策略对信息扩散效果的影响力具有显著性。群体在信息交互中，综合策略的辟谣信息传播效果最好，意见领袖寻求策略次之，关系强度策略最低。对比关系强度策略和意见领袖寻求策略的结果表明，相比群体间关系强度，辟谣信息传播能力对辟谣信息传播起着更为决定性的作用。需要指出的是，群体能否执行综合策略，主要取决于有限群体内部的透明度。个体选择哪一种交互方式进行沟通，很大程度上取决于有限群体内辟谣信息的公开性和透明性，群体信息透明度越高，成员更能够清楚地了解其他个体的传播能力，进而能够更加理性地采取综合策略进行信息交流。因此，在有限群体中，为加强辟谣信息扩散影响，政府应该建立开放性的信息共享、沟通平台，使群体成员能够掌握更多其他个体的辟谣信息传播能力情况，进而采取更有效的交互策略。另一方面，考虑到辟谣信息传播能力对辟谣信息扩散的影响，要培养代表官方权威信息传播的意见领袖，意见领袖所在的群体是一个发生信息交互扩散的有限群体，在公共危机事件下，政府部门通过发挥意见领袖作用，使其代表的群体接触到官方权威信息，这些群体也会在一定概率下感染影响更多的公众，从而抑制谣言的传播。

其次，公共危机事件下信息移出率与信息扩散效果负相关。信息移出率显著影响着辟谣信息传播者比例与扩散速度的大小。这可能是因为个人对该主题信息失去兴趣或对事件的了解程度较低，导致公众对该事件关注较少[25-26]，公共危机事件下，信息移出率的高低取决于个体对辟谣信息关注度和危机事件与个人的利益相关度[27-28]。因此，要降低辟谣信息移出率，政府需明确公共危机事件发生的严峻程度，辟谣信息的发布者应对事件起因和处理过程主动公示，树立大家的责任意识，明确网络上谣言出现的危害价值，降低群众对谣言的认可度，避免造成群体价值观的错误导向。另一方面，对已被证实网络上出现的虚假且危害性较大的信息，可通过不同渠道的宣传普及方式，揭示虚假信息的危害性及其不良意图，调动群体成员在危机事件中相关辟谣信息的传播率，提高辟谣信息的价值认可度。

最后，初始辟谣信息传播者的分布类型决定最终辟谣信息扩散效果。辟谣信息传播者的集群分布限制了群体成员的信息传播范围和能力。公共危机事件发生时，应对社会化媒体谣言传播的方法主要依靠政府和媒体发布的官方辟谣信息进行网络谣言控制，在实践中往往可操作性和及时性不强[29]。这可能是因为一味地追求辟谣信息的权威性，只依靠政府机构发布辟谣信息，将辟谣信息局限在官方媒体中，从而不利于信息的快速扩散。公共危机事件下，由于事件的敏感性，官方信息的垄断式传播会刺激群体成员产生恐慌感，由此会造成大范围的谣言扩散。鉴于此，政府应充分调动起社会各个机构平台的积极性，使更多的团体或个人作为官方权威信息的拥护者，当公共危机事件发生时，网络上均匀分布辟谣信息传播者，辟谣的相关信息会被公众较快接收和获取。

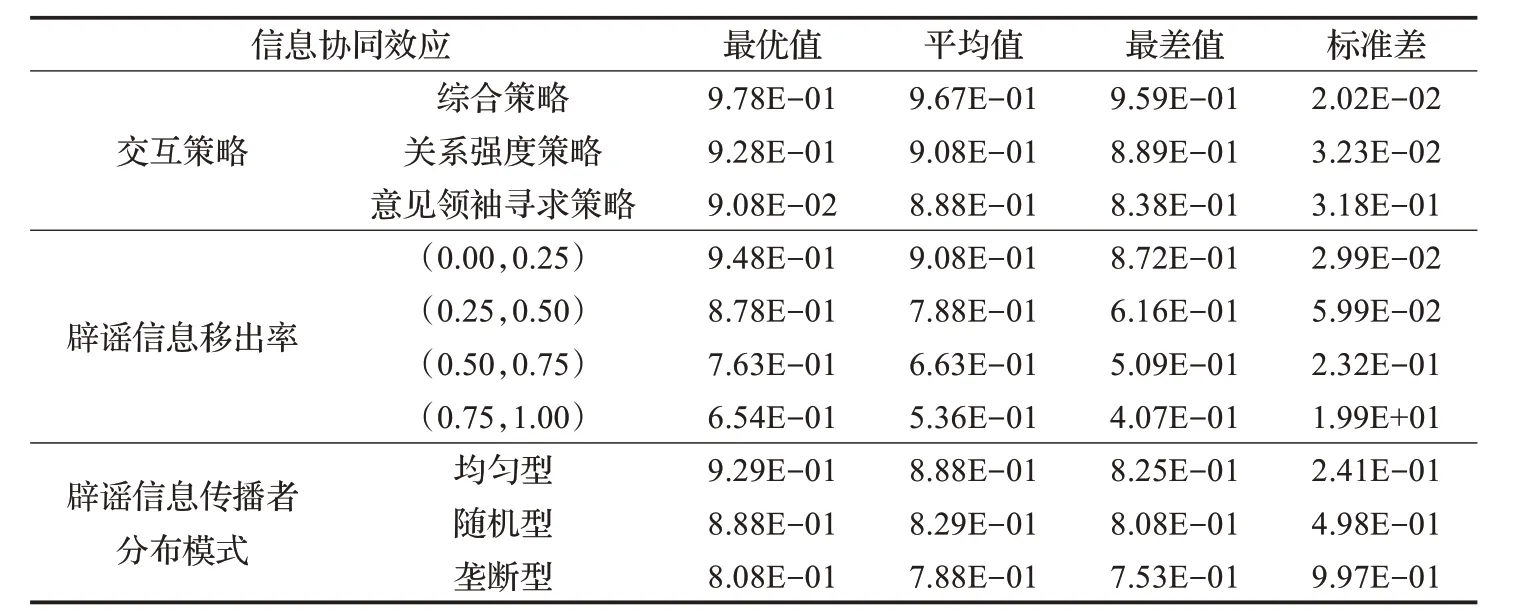
表1 辟谣信息传播者比例仿真结果比较

表2 辟谣信息扩散速度仿真结果比较

6 结束语

本研究借鉴SEIR 传染病模型把群体划分为不同信息状态，根据个体异质性，建立基于异质元胞自动机的辟谣信息传播模型，把不同状态的元胞个体作为研究对象，在信息协同层面研究辟谣信息扩散的机理，能够为监控、预测群体内辟谣信息传播的发展趋势提供可行的方法指导。然而，本研究尚有因素没有考虑，如群体内信息的更新和人员数量的变动，这些问题都是以后需要进一步研究的重要内容。