斜拉桥主塔横梁设计参数对结构静力性能的影响

李德旭 乔文靖 彭晶蓉

（西安工业大学，陕西 西安 710014）

无背索斜拉桥以独特的造型成为城市桥梁的首选桥型之一。独塔无背索斜拉桥主塔只有单侧有斜拉索，以塔身的自重力矩来抵消斜拉索的倾覆力矩。如果主梁采用自重较大的混凝土结构，则需要主塔提供相应较大的倾覆力矩，可以在主塔上部增加主塔横梁以满足要求，既能增加塔身的自重以达到结构整体静力平衡，还能加强两侧主塔之间的联系刚度。

一、工程概况

桥梁全长120m，桥宽30.5m，跨径为80m+40m双索面无背索斜拉桥，桥梁主跨80m，桥塔高65.9m，主梁为预应力混凝土梁，主塔为实心混凝矩形截面，主塔倾角为59°，全桥布置13对斜拉索，塔梁墩固结形式。桥型如图1所示。

图1 桥型布置图

表1 4种横梁设置参数表

二、设计方案及模型建立

（一）4种横梁设置方案

为更加直观地对比横梁设置对结构体系静力特性的影响，共拟定4种对比方案，4种方案的设计参数，如表1所示，表中有横梁方案均为三道横梁，三道横梁均设置在主塔无索区，且相对位置不改变。由于4种方案设计参数的不同，必然引起成桥时刻索力、应力、变形的不同，影响成桥状态。

（二）模型建立

利用有限元软件Midas Civil建立无背索斜拉桥有限元分析模型，主梁和主塔采用梁单元，斜拉索采用只受拉的桁架单元。全桥共划分为296个节点，165个单元。横梁与主塔之间采用刚性连接。按照实际的施工顺序建立施工阶段。

三、静力性能分析

（一）斜拉索受力分析

斜拉桥的高次超静定结构特点决定了结构任意参数的变化，均可引起施工阶段索力值的变化，而成桥索力值对应着最不利荷载组合下的索应力值。

待桥塔有索区施工完毕，施工主塔上部无索区开始进行主塔横梁施工。4种施工方案对应最不利荷载组合作用下的索应力值，如图2所示。

由图2可知，方案1与方案2的横梁压重相同，斜拉索成桥时刻索应力值相同，而方案3较前两者压重小，故索应力力值有所减小，方案4中无横梁时，索应力值最小；横梁配重越大，长索索应力值越大；而4种方案对短索索应力值的影响很小，可忽略不计。4种方案全桥索应力分布规律基本一致。

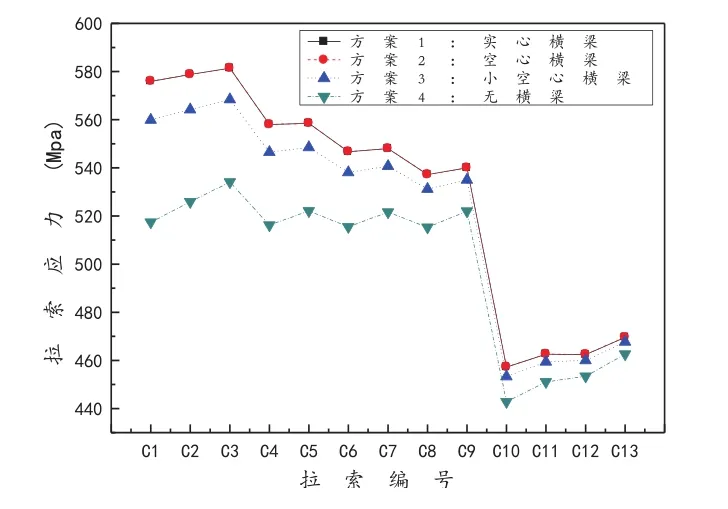
图2 4种方案成桥时刻拉索应力值

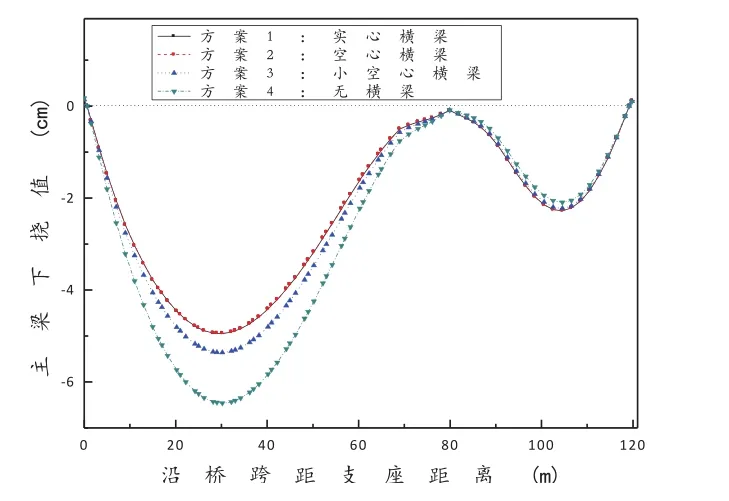
图3 主梁变形图

（二）主梁变形及应力分析

主塔横梁的设置会增加桥塔的自重从而引起索力的增加，主梁受到的向上的竖向分力就会增加，同时主梁受到的向主塔方向的轴力也会增加，因此，主塔横梁的设置会对主梁的应力和变形构成影响。

分析4种方案在承载能力极限状态下的受力，4种方案主梁均全截面受压，且满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG3362-2018)中关于抗压强度的规定。

由图3可知，方案1、方案2的主塔横梁自重相同，故主跨主梁变形相同；方案3主塔横梁自重小于方案1，故主跨主梁的变形值大于方案1；方案4无横梁，故主跨主梁变形值最大。4种方案对边跨主梁的变形影响不大。4种方案的变形值均满足《公路斜拉桥实施细则》（JTG/T D65-01-2007）中关于不对称独塔斜拉桥最大竖向挠度不大于主跨L/500=16cm的要求。

（三）主塔应力及变形分析

图4 方案1～方案4主塔应力图

图5 方案1收缩徐变变形图

图6 方案4收缩徐变变形图

表2 4种方案收缩徐变主塔变形值（单位：mm）

主塔的应力和位移是由自重和索力决定的，主塔横梁的设置增加了主塔的自重，从而对主塔应力和变形造成影响，塔根处的应力对桥塔自重的影响最为敏感，塔顶位移在长期荷载作用下，由于收缩徐变作用有所增加。

方案1和方案2中主塔横梁自重相同，塔根处边跨侧压应力均为2.6MPa；方案3中小空心横梁自重小于方案1，塔根处边跨侧压应力为1.5MPa；方案4中无横梁，由于压重不足，故引起主塔根部边跨侧出现1.7MPa拉应力，具体如图4所示。

在长期荷载作用下，结构由于材料收缩徐变而产生的变形值如图5、图6所示，变形数值如表2所示。主塔向边跨侧变形时方向为正。

如图5、图6和表2所示，方案4由于没有设置横梁，主塔在长期荷载作用下向主跨侧发生了偏移，从而引起主跨侧斜拉索松弛；方案1、方案2、方案3由于上部有横梁压重，结构即使发生收缩徐变变形，主塔也不会向主跨侧发生位移。可见，全混凝土无背索斜拉桥，主塔上横梁的设计十分必要，在满足结构整体静力平衡的前提下，对于同样重量的实心横梁与空心横梁静力性能相差无几，且实心横梁更便于施工。