基于智能优化算法的作战资源部署分析
张诗雅,黄炎焱
(1.南京理工大学自动化学院,江苏南京 210094;2.北京特种机电技术研究所,北京 100012)
0 引言
现今世界,全球瞩目地区战事频发。空袭与反空袭的军事行动是现代战争中的一个核心构成部分,其中含有高新科学技术,而这些技术的存在,决定了战争的最终结局[1]。所以,区域防空作战会逐步成为中国军队在防空作战方面的核心发展方向。对于战前资源部署及战时火力分配问题,这是难题又是核心,进行充分合理的部署及分配可使不同类的防空能力发挥到最大水平,同时,可以对不同种类的防空兵器进行有效的整合,使整体的作战水平提升,这样可确保关键目标的安全度提升,进而使战争打胜的概率提升。
1 面向作战资源部署与分配的总体框架
作战资源部署与分配的统一框架如图1所示。
由图1可知:作战资源与分配需要解决的最终问题就是如何确定作战资源的部署与分配问题。针对此总任务,需要先学习相关的基础理论,在此基础上选择本文所要采用的具体算法,以此确定作战资源与分配的具体数学模型,并对其编程与仿真,最后根据仿真结果确定本文选择算法的优劣。
2 作战资源部署数学模型
2.1 传感器网络部署的考虑
依照所关注的问题角度的差异,无线传感器网络对所覆盖的区域进行控制的类型主要有如下3类:(1)区域覆盖;(2)点覆盖;(3)棚栏覆盖[2]。通常状况下,动态部署主要出现于移动无线传感器网络内,其节点需经自身的运动,使监测区域的覆盖率与连通度予以提升。进行动态部署时,移动节点允许为网络内的任意节点。
2.2 火力单元部署的考虑
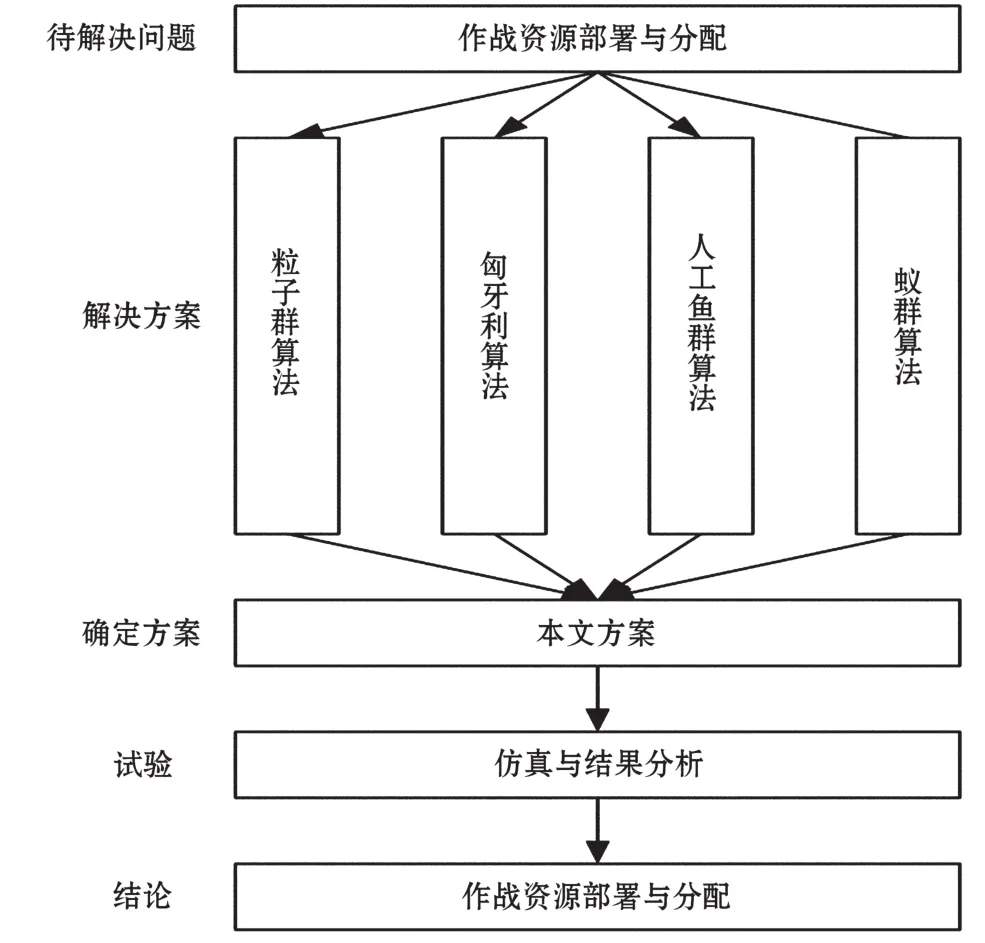
图1 作战资源部署与分配统一框架
若要得到部署备选位置点,需对部署区域进行划分,变成离散区域与连续区域。对于离散区域,对部署区域经网络分割,变成有限个网络点,之后将形成的网络点用于进行部署的位置,同时,这些点也可以用于对火力覆盖效果评价时的取样点[3]。对于网络化防区,对网络尺寸进行分割要依照防区部署所需进行合理化设置。网络设置的越加密集,部署的位置就会越多,计算量会提升,质量也会对应的提升[4]。位于连续区域内,火力节点允许部署于区域内的所有位置,确保最优解位于搜索空间内。需要说明的是,连续空间内有比较均匀的搜索,却不如不均匀离散化的区域搜索的效率高[5]。
2.3 基于改进粒子群算法的传感器网络部署模型
虚拟力算法(Virtual Force Algorithm,VFA)是通过虚拟力在物体上产生的效果,达到优化的目的[6]。因此,虚拟力的介入能够确保节点间的距离维持在某个数值上,使网络的连通性保持平稳。
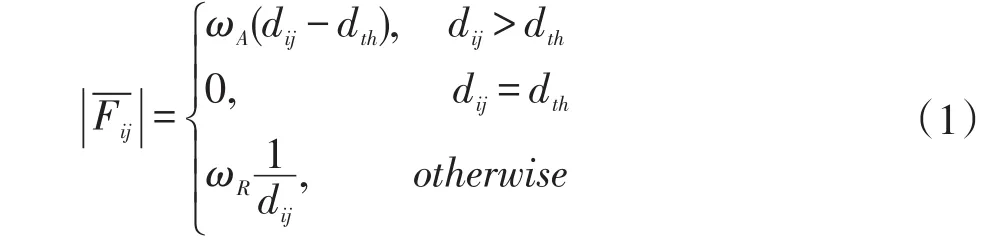
其中,dij是节点i与j间的欧氏距离,dth是阈值,即节点间的最佳距离,ωA,ωR依次是引力和斥力的系数。
式(1)的得来,主要是成簇之后,在放首节点处,会有对应的虚拟力合力,它会对簇中的节点方向的运动进行控制,表示式为:

在成簇之后的单一簇中的节点在数量上是不同的。其节点总量与距离会对后续的部署有直接影响。所以,把簇中节点个数同簇中距离转变成参数使用至簇中虚拟力的运算中,能够获取簇中斥力值:

2.4 基于匈牙利算法的火力单元部署数学模型
基本假设:我方编队有n类武器,敌方编队有m个目标,第i类武器对敌编队第j个目标的单枚毁伤概率为Pijd(i=1,…,n;j=1,…,m)。此类武器总量是ci(i=1,…,n)。决策变量x0为我方第i类武器对敌编队第j个目标的发射数量,vj为敌编队第j个目标的价值。
第i类武器对第j类目标的全体毁伤概率pij,既同被攻击目标相关,又同对该目标齐射武器及种类相关,由此表示为:

其中,j为被攻击目标的种类。
目前为止,有关分配的模型主要有极大化目标毁伤价值模型、极大打击效果模型、极小化弹药消耗模型3类,主要是针对目标数量及其战斗力的差异,对武器攻击力进行划化。本文选用极大化目标毁伤价值模型,如下所示。
因武器突防时,第i类武器对敌内的第j个目标造成的毁伤率为:

对应的敌方的第j个目标,它的整体毁伤率为:
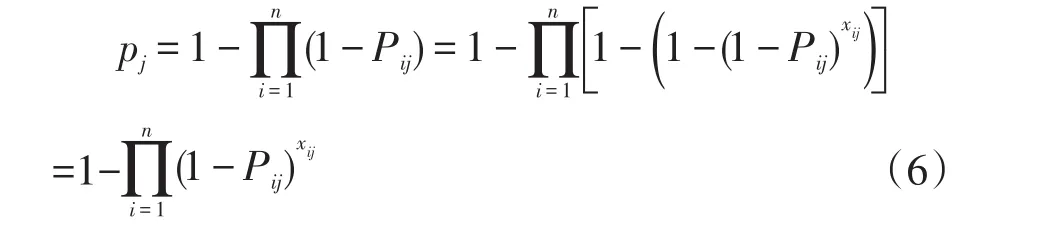
由上式(5)和(6)有:
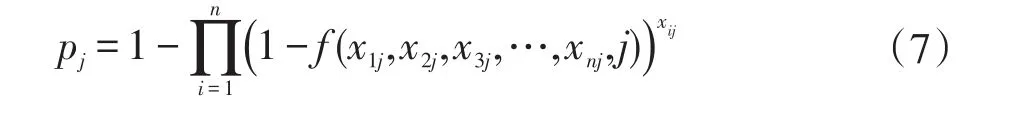
假定目标事件进行打击时的期望为α(0<α<1),则极大化毁伤价值下的目标规划模型是:
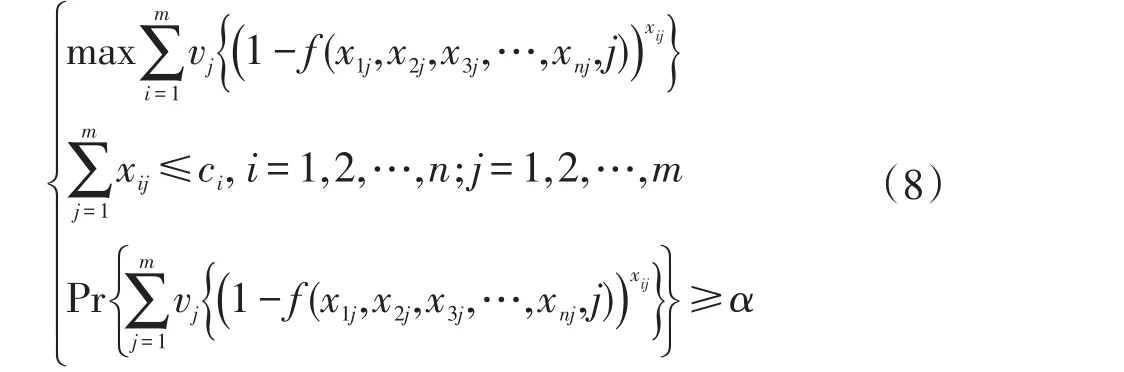
式中,xij是正整数;i=1,2,…,n;j=1,2,…,m;Pr{·}为事件的概念。
3 基于智能优化算法的作战资源部署仿真及其分析
3.1 基于改进粒子群算法的传感器网络部署优化流程
传感器网络部署优化流程,如图2所示。
(1)初始化。把网络内的各移动节点看作为粒子群优化时的运动粒子。此粒子的位置受控于随机撒布,而节点仅受控于随机初始化时本身的初始移动速度。
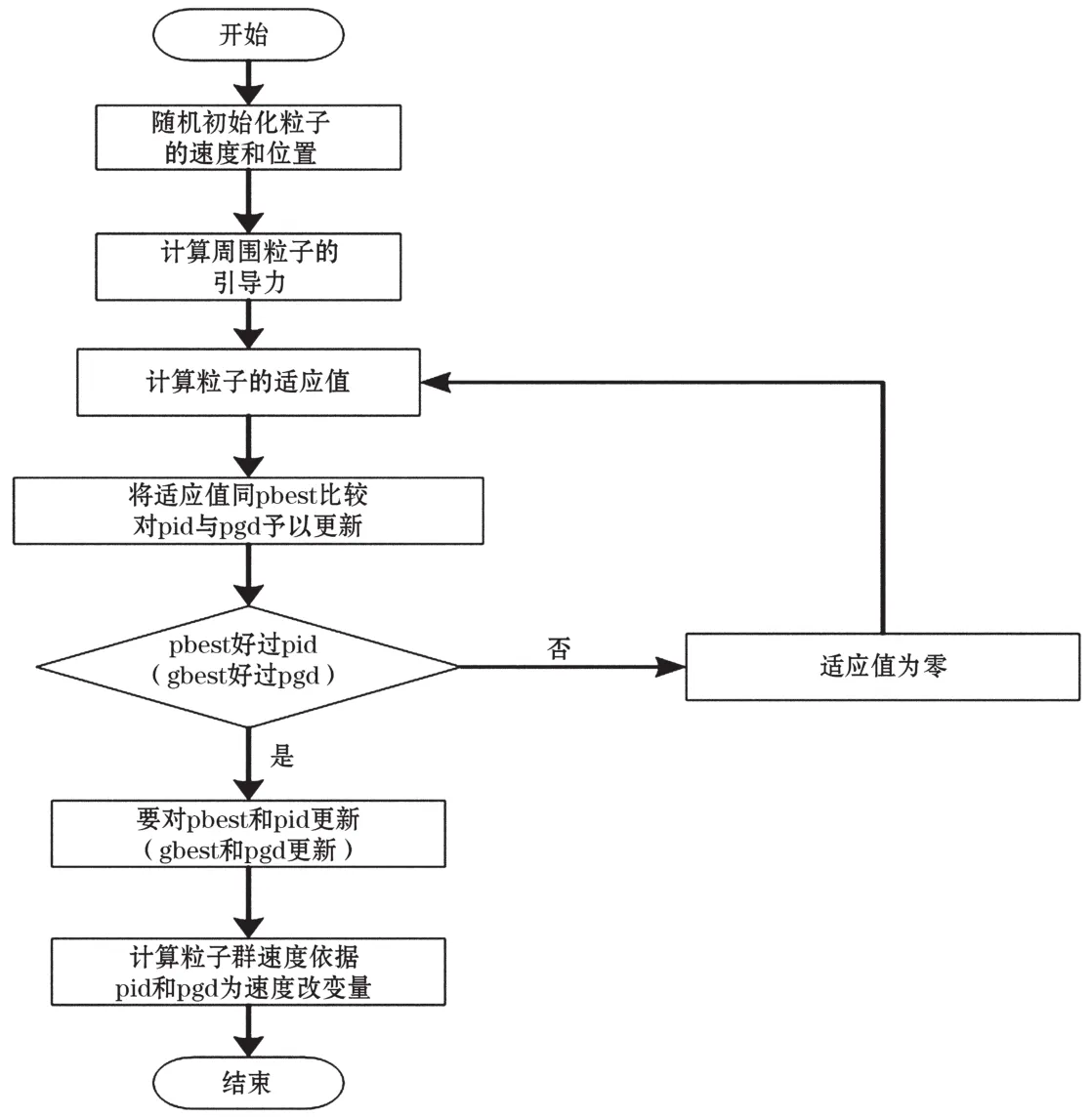
图2 传感器网络部署优化流程
(2)引导力计算。算出周围节点对本身虚拟力的作用。依照此章中列出的虚拟力公式,对周围节点形成的全力予以计算,同时,把受作用力变换成某一节点的速度改变量。算出引导力同粒子群协同作用下速度的改变量。
(3)节点移动。依照粒子速度及每轮移动时间,对节点位置进行变更。
(4)适应值计算。借助适应值函数算出节点位置目前的适应值,同时把本身的适应值予以广播。
(5)更新pid与pgd。把粒子目前的适应值同本身最优适应值pbest进行比对,如果好于pbest,需对pbest与pid进行变更,相同地,把本身目前的适应值同局部最优适应值进行比对,如果好于gbest,需对gbest和pgd进行变更。
(6)判断适应值。如果节点当前适应值是零,粒子处于停止状态,需等下一轮的适应值运算,跳至第四步。如果适应值非零,继续下一步,跳至第七步。
(7)粒子群速度计算。依照pid与pga算出粒子群优化算法中速度的改变量。跳至第二步。
3.2 基于匈牙利算法的火力单元部署优化流程
火力单元部署优化流程,如图3所示。
(1)对不平衡指派变换成平衡指派问题,假定部分虚拟的行(列)向量,其他用零予以补充,最终得到优势矩阵C的n×n矩阵。
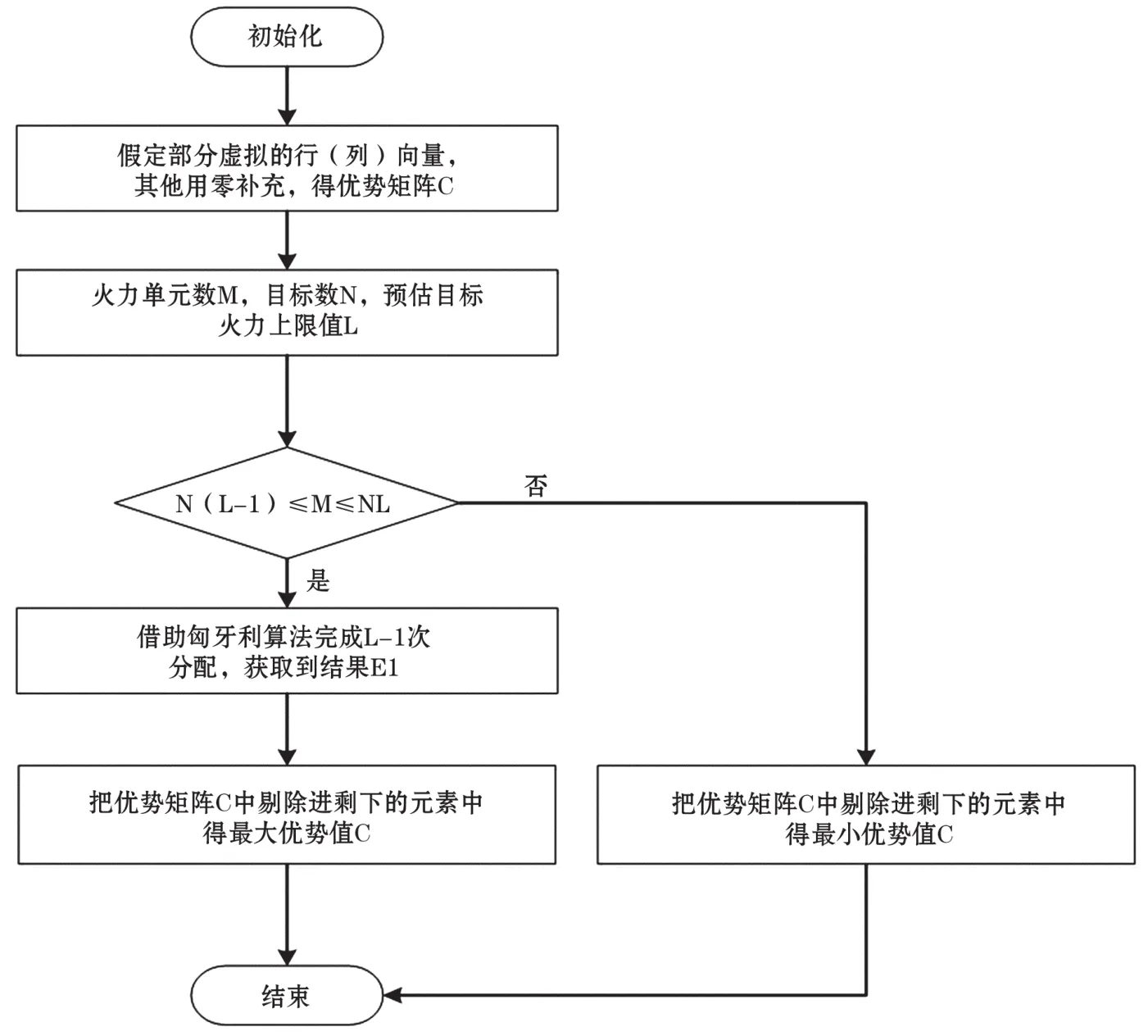
图3 火力单元部署优化流程
(2)对目标的火力问题进行预估,得到上限值L,当火力单元数是M,目标数是N,若N(L-1)≤M≤NL,借助匈牙利算法完成L-1次分配。同样地,若N(L-2)≤M≤N(L-1),借助匈牙利算法完成L-2次分配。获取到结果E1;也可得到下限值L,借助匈牙利算法完成L次分配,获取到结果E1。进行研究时,运用第一种完成分配。
(3)把之前分配好的火力单元同符合要求的火力总量的目标在优势矩阵C中剔除,进而在剩下的元素中获取最大优势值C`。那么,把第i个火力单元对应于第j个目标进行分配,且把对应的行与列进行删减。之后在剩下的矩阵中得到上限值作分配,到每个目标均符合要求或每个火力单元均有分配止。
3.3 仿真与分析
借助Mat1ab2011仿真出所提及的算法,同时,在相同的仿真环境中,对改进粒子群算法作仿真且进行对比。设定的仿真监测区域的大小为,内部含有140个无线传感器节点,假定有90个为固定节点,有50个为移动节点。前者在节点监测区域内是随机均匀分布,而后者则是在其中正太分布,则其期望为60,方差为20。仿真结果如图4所示。
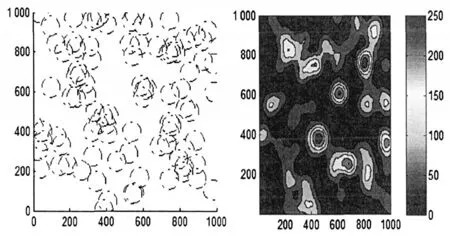
图4 固定节点监测区域布示意
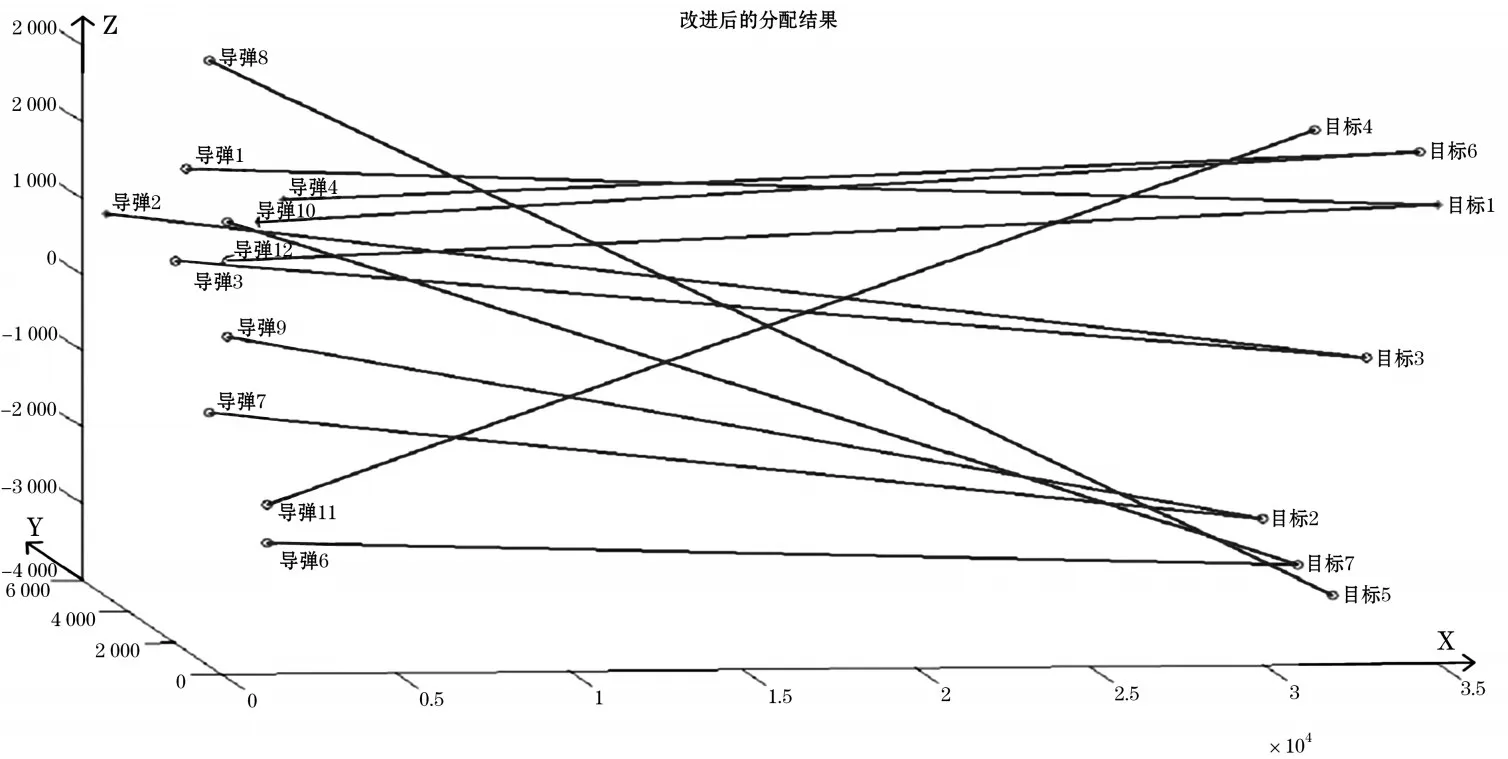
图5 火力单元分配结果
假定有12枚导弹攻击7艘舰艇目标,借助匈牙利算法仿真结果与网络不佳时获取的优势矩阵作分析,如图5所示。
改进之后的目标3所分配到的只有导弹2与5,因为这两枚导弹内只含有目标3的信息,对应的对目标3进行假定的饱和数是2,因此,原定的分配方案内的导弹3与10会被提取,依照优势矩阵作二次分配,由其矩阵内的导弹3可知,导弹3相对于目标3有很大优势值,然而,因目标3完成了分配,所以,要对目标3作优势值变零处理,之后二次获取最大优势值,到有新分配结果止。同样地,导弹10也是此种操作。经对比可知,借助改进之后的分配算法,要符合目标饱和攻击的前提下,再次对过量的弹药作二次分配,防止局部过度分开而出现饱和状况。

