空间索面悬索桥空缆线形的精确解析法

张 娜，丁 松，吕 阳

(1.北京城建设计发展集体股份有限公司，北京 100037；2.中交基础设施养护集团有限公司，北京 100018；3.燕山大学建筑工程与力学学院，秦皇岛 066004)

空间索面悬索桥吊杆和主缆互相耦合，形成一个三维空间体系，与平行索面悬索桥相比较，显著提高悬索桥横向承载力和抗扭刚度。目前空间索面悬索桥由于结构优美、造型独特，正在越来越多的用在中小跨径悬索桥上。

主索鞍的修正是影响悬索桥空缆线形计算精度的主要因素。悬索桥空缆线形的分析方法主要分为有限元法和解析法。有限元法采用无限细分的只受拉杆单元模拟主缆，采用一个节点(理论IP点)来连接各跨主缆，在成桥分析的基础上，拆除吊杆并释放塔顶IP点顺桥向约束，将IP点的偏移量作为主索鞍的偏移量。这种算法忽略了主索鞍的影响，从而无法精确计算悬索桥的空缆线形。针对悬索桥主索鞍的修正，已经有很多人进行了研究，解析法由于其计算灵活方便被提出来，虚交点法可以考虑主索鞍的立面曲线，从而精确地计算平行索面悬索桥的空缆线形。而空间索面悬索桥的主索鞍同时存在平面弯曲和竖面弯曲(见图1)，此时通过传统的虚交点法无法考虑主索鞍的平面弯曲修正，难以保证空间索面悬索桥空缆线形的计算精度。

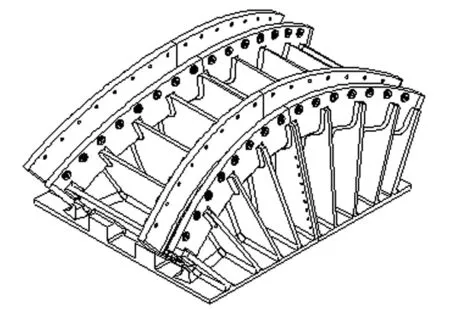
图1 空间主索鞍构造图

1 空间索面悬索桥空缆线形的计算

1.1 传统解析法的局限性

考虑到空间索面悬索桥的主索鞍同时存在平面弯曲和竖面弯曲，如何精确计算主索鞍切点和保证各跨主缆无应力长度与成桥一致为其空缆线形计算的关键。

传统的解析法(见图2)仍然将边跨和中跨主缆采用一个节点来连接。考虑主索鞍的情况下，主索鞍位置计算和主缆迭代修正过程如下。

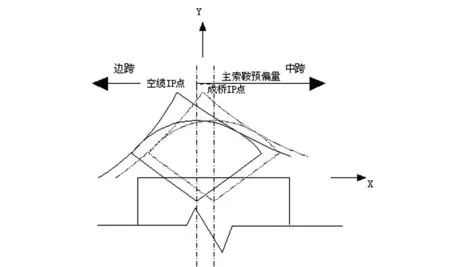
图2 传统解析法计算图示

(1)确定一组IP点的预偏量；

(2)假定理论IP点之间的主缆无应力长度不变计算各跨主缆水平力和竖向力；

(3)根据主缆与主索鞍之间的相对关系，求解主索鞍切点、主索鞍圆心、悬空段主缆无应力长度和主索鞍圆弧段主缆无应力长度；

(4)根据计算得到的各跨主缆无应力长度与成桥主缆无应力长度之差修正理论IP点之间的无应力长度；

(5)重复(3)-(4)直至主缆各跨无应力长度为成桥主缆无应力长度；

(6)计算主索鞍圆心的位置，得到主索鞍的预偏量。

以上算法由于只考虑了主索鞍的竖面弯曲修正，而只能精确计算平行索面悬索桥的空缆线形，且需要求解八个非线性方程组，计算比较复杂。

1.2 空缆线形计算方法的改进—KJKL法

KJKL法(见图3)以边跨和中跨主缆纵向水平力相等为目标，直接采用圆弧修正的各跨主缆无应力长度。精确计算主缆与主索鞍的切点，从而得到精确的空缆线形。主要计算步骤如下：

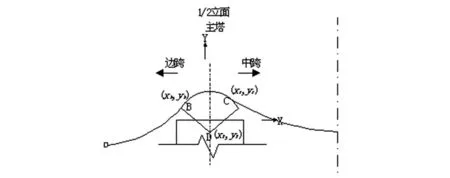
图3 KJKL法计算图示

(1)以主索鞍不设预偏量作为迭代初值。

(2)求解此预偏量下主缆边中跨切点。

①以成桥主缆边中跨切点为初值进行迭代，根据假定的切点和主索鞍的空间曲线求得其与主索鞍鞍槽相接触的主缆无应力长度和悬空段主缆无应力长度；

②求解悬空段主缆在假定切点处的切线夹角

③求解主索鞍鞍槽在假定切点处的切线夹角；

④求解鞍槽切线夹角与悬空段主缆切线夹角之差并采用影响矩阵法修正边中跨切点，直至角度差为零，得到此预偏量各跨主索鞍切点。

(3)求解主缆各跨纵向水平力之差，采用影响矩阵法修正主索鞍预偏量。直至各跨纵向水平力相等得到主索鞍预偏量和空缆线形。

基于KJKL法编制相应的Matlab程序，程序全面考虑了空间索面悬索桥的主索鞍的空间尺寸，并精确计算主索鞍切点，保证各跨主缆无应力长度不变，得到准确的空缆线形。程序流程图如图4所示。

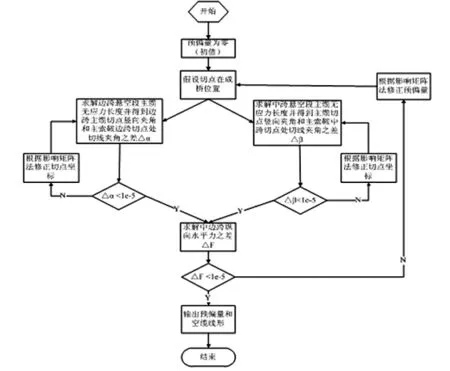
图4 KJKL法程序流程图

1.3 KJKL法的优越性

从以上分析可以看出，KJKL法直接采用圆弧修正后的主缆无应力长度，与传统的虚交点法相比，计算更加简单，无需求解复杂的非线性方程组，能够精确求解平行索面悬索桥和空间索面悬索桥的空缆线形。

2 算例分析

2.1 工程概况

以松原市天河大桥北汊桥为例进行分析。松原市天河大桥北汊桥为我国跨径最大的双塔空间索面自锚式悬索桥，跨径布置为100 m+266 m+100 m(见图5)。

材料特性见表1。

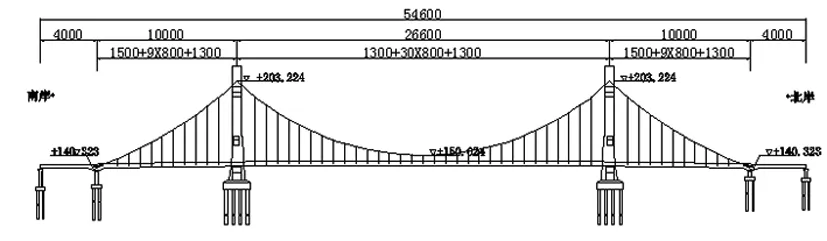
图5 松原市天河大桥北汊桥桥跨布置图

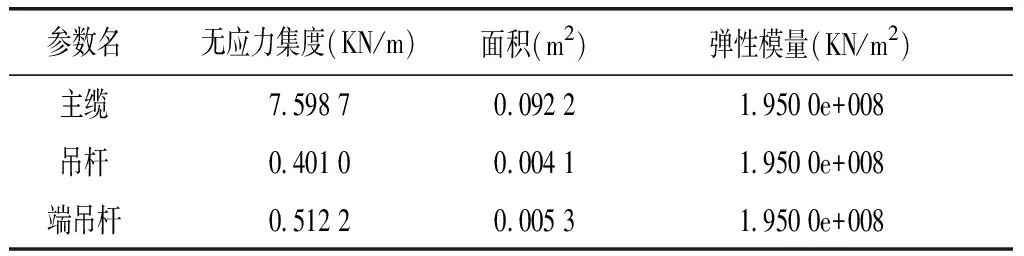
表1 材性参数表

主缆成桥矢跨比为1/5，主缆从塔顶理论IP点横向间距1.5 m逐渐过度至跨中26.8 m形成空间索面自锚式悬索桥，桥面设纵坡为2.2%半径为12 000 m的竖曲线。主索鞍竖面半径为3.8 m，平面半径为10 m。

根据成桥计算结果我们得到主缆无应力长度如表2。

表2 松原市天河大桥北汊桥主缆中心索股无应力长度

2.2 预偏量和空缆线形分析

针对虚交点法和KJKL法分别编制相应的Matlab程序，经过计算得到两种方法所得预偏量如表3。

表3 两种方法计算所得预偏量

KJKL法和虚交点法分别迭代了5次和6次得到了结果，表明KJKL法的收敛性很好。

为了使两种方法所得空缆线形有可比性，将预偏量统一设置为47.3 cm(现场预偏量设置参数)，求解在同样预偏量的条件下两种方法的空缆线形，具体分析结果如表4。

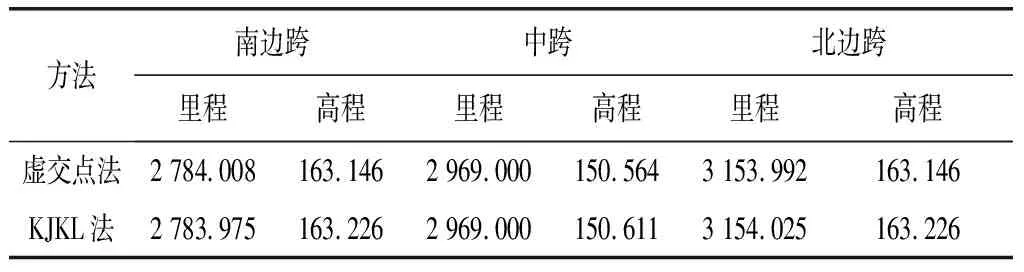
表4 两种方法所得空缆线形(m)

为了验证KJKL法的准确性，将KJKL法结果利用Midas/Civil进行建模分析。

由于Midas/Civil无法准确模拟主索鞍，建模时根据KJKL法得到的切点坐标、观测点坐标、后锚点坐标和各段主缆无应力长度建立有限元模型，观察其在自重作用下位移是否为零，有限元模型在自重作用下的位移不超过2 mm，表明KJKL法计算出的空缆线形精度很高。

松原市天河大桥北汊桥根据KJKL法的计算结果进行基准索股架设，架设完成后，北塔主索鞍顶部标志点准确就位，南塔塔顶标志点向边跨调整了2 cm，同时南后锚面利用锚杯调节主缆长度缩短了2 cm，为施工误差导致。表明KJKL法非常可靠。

2.3 结果分析

根据以上计算结果和现场实测情况我们可以看到两种算法主索鞍预偏量的结果相差较小，可以满足要求，在同样的预偏量下，虚交点法得到空缆线形均比KJKL法较低，在中跨跨中低了4.7 cm。而在边跨主缆标志点无论是里程还是高程都有差别。显然虚交点法精度无法保证成桥线形，可以看出精确考虑空间主索鞍尺寸对空间索面悬索桥空缆线形的影响的必要性。

3 结 论

本文对传统虚交点法在计算空间索面悬索桥空缆线形的问题进行了充分研究，指出了其在空间索面悬索桥上应用的不足，并提出一种可以考虑主索鞍尺寸的精确解析法(KJKL)来计算空缆线形，这种算法可以精确考虑平面主索鞍和空间主索鞍的具体尺寸，从而能得到精度更高的空缆线形。并以松原市天河大桥北汊桥为例进行了分析计算。分析表明：虚交点法无法保证精确的空缆线形，空间索面悬索桥必须精确考虑主索鞍的影响，KJKL法具有计算速度快、收敛精度高的特点，可以运用于空间索面悬索桥空缆线形的计算。