采气速度对气田产量峰值预测模型的影响分析

方一竹 ，余 果，李海涛，徐 凌，陈艳茹，付 玉，王 升

（1.中国石油西南油气田勘探开发研究院，四川成都 610041；2.西南石油大学，四川成都 610500）

在气田开发的实际工作中，对产量、累积产量和可采储量的正确预测，始终是油气藏工程师的重要任务。油气田开发指标预测的准确性和可靠性，会影响到编制中长期开发规划的效果，对于指导气田方案编制具有重要的参考意义[1]。从预测方法的本身来说，模型预测法具有较为普遍的适用性，不受气田开发阶段和气田类型的影响，已在天然气产量预测领域得到广泛应用[2-5]。我国著名地球物理学家翁文波于1984 年在专著《预测论基础》中提出泊松旋回模型（又称翁氏模型）[6]，为我国油气田产量预测奠定了几种油气田产量预测模型的对比基础[7]。之后，其他学者相继提出了多种预测模型[8]，包括广义翁氏模型、HCZ 模型[9]、瑞利（Rayleigh）模型[10]、威布尔（Weibull）模型[11]、哈伯特模型[12]、胡张陈模型[13]、对数正态分布模型[14]等预测模型。本文主要研究了采气速度与4 个模型参数的影响因素，利用预测模型建立起采气速度和产量曲线特征之间的联系。

1 建立油藏数值模拟模型

为研究模型的影响因素，需建立油藏数值模拟模型。从文献可以看出，影响气藏产量的因素主要有：渗透率、采气速度、地层压力、有效厚度、井控半径等，对于已经投入生产的气藏，采气速度具有较高的研究价值。本文利用数值模拟方法建立典型气藏模型，开展采气速度影响研究。机理模型基本参数（见表1、图1）。

表1 气藏机理模型参数表

表2 气藏采气速度设计表

按照设计好的模型参数（见表2）建立模型后进行全生命周期的生产模拟，分别得到不同的年产量数据。利用各个模型，结合数值模拟数据进行产量和累积产量的预测，使用MATLAB 软件编程，得到预测公式和预测图形。部分实验数据的预测曲线图（见图2、图3）。

图1 气藏机理模型

图2 HCZ 模型年产量拟合

图3 HCZ 模型累积产量拟合

2 采气速度影响分析

2.1 HCZ模型

1995 年，胡建国、陈元千、张盛宗提出了HCZ 模型预测油气田产量和累积产量。HCZ 模型预测产量和累积产量的表达式为：

模型的半对数线性表达式为：

根据气田的实际生产数据，可由式（3）和式（4）分别线性回归求得截距和斜率，进而求得模型的预测公式中参数a，b 和NR的值，即可得到气田的HCZ 模型的具体预测公式。HCZ 模型的产量计算公式（1）是年产量Q 关于时间t 的函数，影响曲线形态的参数共有a，b和NR。分别改变三个参数的大小，绘制出对应的年产量曲线（见图4）。

图4 参数对HCZ 模型曲线形态影响

参数a 增大使峰值产量发生时间滞后，表现为图形峰值右移；对可采储量没有影响。参数b 增大使得峰值产量增大，峰值时间提前，表现为图形峰值左移和上移；对可采储量没有影响。参数NR增大使峰值产量增大，峰值时间不变，表现为图形峰值上移；使可采储量增大。

在不同采气速度下，对得到的年产量数据模拟，分别得到对应的HCZ 模型预测公式。根据采气速度和模型参数分析结果可知，在实验因素变化范围内（见图5）。

参数a 与采气速度反相关。结合图4 可知，当采气速度增大时，产量的峰值发生时间提前，上产与递减均变快；峰值大小不变化。参数b 与采气速度三次方正相关。结合图4 可知，当采气速度增大时，产量的峰值发生时间提前，上产与递减均变快，峰值升高。参数NR与采气速度正相关，具有较高的线性相关性。结合图4 可知，当采气速度增大时，产量的峰值升高。

2.2 瑞利模型

瑞利模型由陈元千等建立，可用于预测油气田的产量、累积产量、可采储量、最高年产量及其相应的开发时间和累积产量。应用实例证明该模型有广泛的有效性。瑞利模型预测产量和累积产量的表达式为：

图5 采气速度对HCZ 模型参数的影响

利用瑞利模型进行各项预测必须先确定模型常数a 和c。为此，将式（5）两端先除以t 再取常用对数，得：

可改写为如下形式：

根据气田的实际生产数据，由式（8）进行线性回归后，求得直线截距α 和斜率β 即可确定常数a 和c 的数值。瑞利模型的产量计算公式（5）是年产量Q 关于时间t 的函数，影响曲线形态的参数有a 和c。分别改变两个参数的大小，绘制出对应的年产量曲线（见图6）。

参数a 增大使产量峰值升高，峰值发生时间不变；使可采储量增大。参数c 增大使得产量的峰值增大，峰值发生时间提前，表现为图形峰值左移和上移；使可采储量增大。

在不同的采气速度下，对得到的年产量数据模拟，分别得到对应的瑞利模型预测公式。根据采气速度和模型参数分析结果可知，在实验因素变化范围内（见图7）。

参数a 与采气速度的平方正相关。结合图6 可知，当采气速度增大时，产量的峰值升高，峰值发生时间不变。参数c 与采气速度的平方反相关。结合图6 可知，当采气速度增大时，采气速度增大使峰值降低，峰值发生时间提前。

2.3 对数正态分布模型

对数正态分布模型是基于对概率统计学中对数正态分布建立的预测油气田产量、可采储量、最大年产量及其发生时间的数学模型。对数正态分布的数学模型为：

对式（9）等号两端取常用对数得：

若给定不同的α，利用式（10）进行线性试差求解，对于能够得到最大相关系数的直线的α 值，即为要求的正确的值。再通过线性回归，可以分别得到可采储量NR和参数β 的数值。对数正态分布模型的产量计算公式（9）是年产量Q 关于时间t 的函数，影响曲线形态的参数有α、β 和NR。分别改变三个参数的大小，绘制出对应的年产量曲线（见图8）。

参数α 增大使峰值产量降低，峰值发生时间滞后，表现为图形峰值向右下方移动。参数β 增大使得峰值产量增大，峰值发生时间提前。参数NR增大使峰值产量增大，峰值发生时间不变，表现为图形峰值上移。

图6 参数对瑞利模型曲线形态影响

图7 采气速度对瑞利模型参数的影响

图8 参数对对数正态分布模型曲线形态影响

图9 采气速度对对数正态分布模型参数的影响

在不同的采气速度下，对得到的年产量数据模拟，分别得到对应的对数正态分布模型预测公式。根据采气速度和模型参数分析结果可知，在实验因素变化范围内（见图9）。

参数α 与采气速度的三次方反相关。结合图8 可知，当采气速度增大时，年产量的峰值升高，峰值发生时间提前。参数β 与采气速度的三次方反相关。结合图8 可知，当采气速度增大时，年产量的峰值升高，峰值发生时间提前。参数NR与采气速度之间没有明显的相关性。

2.4 胡张陈模型

胡张陈模型是基于对大量油气田开发实际动态资料的统计研究，建立的一种预测油气田产量、累积产量、可采储量、最高年产气量及其发生的时间的模型。该模型不仅适用于油气田产量存在单峰的情形,而且也适用于油气田投产之后持续递减的情形。胡张陈模型的数学模型为：

对式（11）和式（12）处理可得：

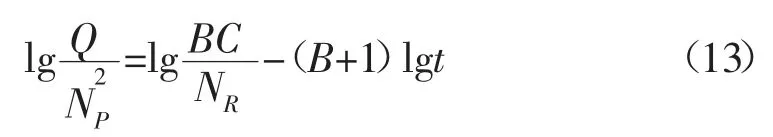
对气田的年产量与累积产量平方之比与生产时间之间的双对数进行线性回归，即可得到模型参数。胡张陈模型的产量计算公式（11）是年产量Q 关于时间t 的函数，影响曲线形态的参数有B、C 和NR。分别改变三个参数的大小，绘制出对应的年产量曲线（见图10）。

参数B 增大使峰值产量升高，峰值发生时间提前，表现为图形峰值向左上方移动。参数C 增大使得峰值产量稍微降低，峰值发生时间滞后。参数NR增大使峰值产量增大，峰值发生时间不变，表现为图形峰值上移。

在不同的采气速度下，对得到的年产量数据模拟，分别得到对应的胡张陈模型预测公式。根据采气速度和模型参数分析结果可知，在实验因素变化范围内（见图11）。

参数B 与采气速度的三次方正相关。结合图10 可知，当采气速度增大时，年产量的峰值升高，峰值发生时间提前。参数C 与采气速度反相关。结合图10 可知，当采气速度增大时，年产量的峰值升高，峰值发生时间提前。参数NR与采气速度正相关。结合图10 可知，当采气速度增大时，年产量的峰值升高，峰值发生时间不变。

图10 参数对胡张陈模型曲线形态的影响

图11 采气速度对胡张陈模型参数的影响

3 结论

（1）使用HCZ 模型、瑞利模型、对数正态分布模型和胡张陈模型对气藏产量进行预测时，气藏采气速度的变化会体现在预测模型的参数变化中。

（2）气藏采气速度的变化，与预测模型的参数之间具有紧密的数学联系。因此在气田开发过程中，可提前预测采气速度改变对气田峰值的影响。