基于PCA优化的PSO-FCM聚类算法①

陈 诚,刘振宇

(南华大学 计算机科学与技术学院,衡阳 421001)

作为传统聚类算法模糊C-均值聚类算法(Fuzzy C- Mean clustering algorithm,FCM)的一种优化算法,引入了粒子群优化算法(Particle Swam Optimization,PSO),粒子群模糊聚类算法(Particle Swarm-based Fuzzy Clustering algorithms,PSO-FCM),通过PSO 算法的收敛速度快,粒子收敛由自身最优位置和群体最优位置相结合,在一定程度上解决了FCM 对初始值敏感,对噪声数据敏感,容易陷入局部最优解的缺点.如今,随着数据量多样化,复杂化,多类别化,PSOFCM 只是单一优化初始聚类中心选取问题,没有合理的限制粒子的移动,并不能更好优化好FCM 算法面对多聚类问题时[1-7].

为了解决上述问题,引入主成分分析(Principal Component Analysis,PCA),本文提出基于PCA 优化的粒子群模糊聚类算法(PCA-PSO-FCM),通过PCA 对数据各维度的分析和评定综合给出一个权重值,粒子各维度会根据该调整权重速度和方向.本文详细介绍了PCA-PSO-FCM,并且与FCM 和PSO-FCM 进行了实验结果的比对,从实验上来看,本文的算法在多种群聚类问题上性能更好,是一种很有潜力的聚类算法.

本文结构如下:第1 部分主要对已有的算法的研究成果进行简要分析总结;第2 部分对于本文的优化算法进行详细说明;第3 部分说明实验过程相关细节,设定参数以及实验结果的分析;第4 部分总结全文.

1 算法介绍

PSO-FCM 算法是模糊均值聚类算法基础上的优化算法,传统的模糊C 均值算法的结果精度,对初始中心的选取有很严格的要求,并且容易陷入局部最优解.为了解决这个问题,国内许多学者,利用具有集体智能的粒子群优化算法,与传统模糊C 均值算法结合.利用PSO 算法求解初始聚类中心,进而优化了FCM 依赖初始中心的问题;利用PSO 算法中,粒子个体与粒子群体之间关系,粒子整体移动的速度可以调节,进而降低了FCM 容易陷入最优解的可能性.

1.1 PSO-FCM 算法

PSO-FCM 算法是基于数据样本之间的模隶属矩阵建立的聚类算法.算法的核心思想是:n个文本样本为X=(x1,x2,···,xn),划分为C =(c1,c2,···,cn),p个聚类中心,计算出每个文本的隶属度 μij,μij表示第j个样本隶属于第i个样本的隶属度.

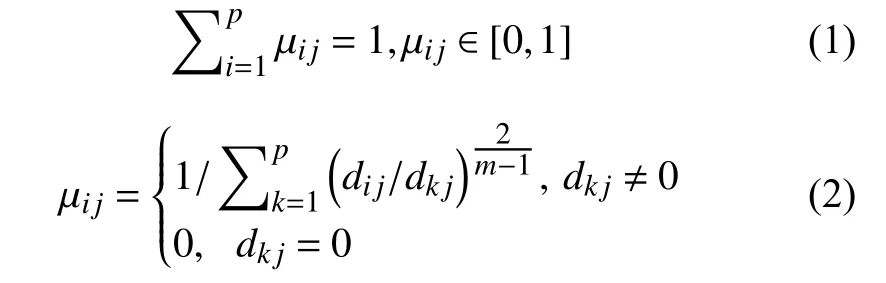
根据每个样本的隶属度值计算出适应度函数值:

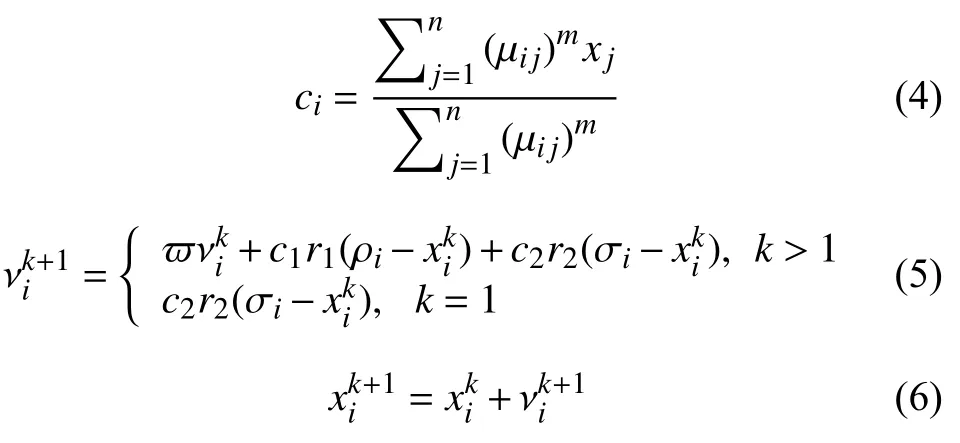
式中,m是加权指标,m＞1,xj-νi表示样本xj到第i个样本中心的聚类,PSO-FCM 算法适应度函数Jm值越小说明性能越好;ρi是粒子最优适应度的位置,σi是群体最优适应度函数,c1和c2是 学习因子;r1和r2是[0,1]之间的随机因子数,ϖ是惯性权重.

2 算法优化

2.1 PCA 算法

随着数据量的爆发和激增,数据类型的增多,数据复杂程度的加深,PSO-FCM 算法的性能无法完全发挥.于是近年来有学者对该算法进行了再度优化,陈寿文[8]提出利用混沌粒子融合粒子群模糊聚类算法(CCPSOFCM),余晓东等[9]利用直觉模糊核优化粒子群模糊聚类算法.雷浩辖等[10]利用遗传算法(GA)与PSO 混合优化的遗传粒子群模糊聚类(GA-PSO-FCM).这些学者都是针对于PSO-FCM 算法依赖初始解这个问题上进行的优化.算法核心是通过比较隶属度,移动该粒子并决定属于哪一类,但是在各维度上面的移动上并没有一个主次之分,在各维度上的移动全部是随机因子数决定.随着聚类中心数量的增加,隶属度矩阵上,各聚类中心隶属度值接近,粒子各维度移动不受限,这样导致部分粒子可能会被分入,与正确聚类中心隶属度值接近的错误聚类中心中的问题.在维度增加,聚类中数量增加,这个问题会越来越频繁出现.

为了在一定程度降低上面的问题出现的可能性,本文引入了PCA[11-13]算法对原算法进行优化,PCA 是一种统计分析的方法,通过正交变换将具有一定相关性的向量转为彼此正交,且互相独立的一维新向量(即主成分).每个主成分都是初始变量的线性组合,没有冗余信息,构成空间的正交基.主成分分析法可以简化统计数据,揭示特征变量之间的关系.在本文优化中并没直接对数据进行降维,根据PCA 中主成分贡献率公式:计算出样本空间各维度之间的贡献率η=(η1,η2,···,ηn),进一步优化PSO-FCM 算法中速度的的迭代公式:

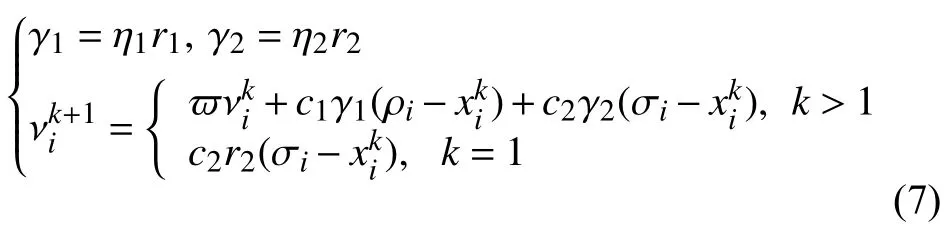
2.2 优化算法实现

?

?

3 实验分析

3.1 实验数据处理

在测试算法的性能,本文选择UCI 机器学习数据库中,Wine,Breast Tissue,Dermatology,以及Glass Identification,每一组数据都进行了清洗,并且都做了使用线性函数归一化将数据集进行标准化处理.各维度的权重是通过主成分分析得出各维度贡献率,数据集参见表1 数据集表.

表1 实验数据集表

3.2 模型评价指标

通过对比本算法与K-近邻(KNN),FCM,PSO-FCM在数据集训练的结果.本文采取的评价算法性能的指标:调整互信息(Adjusted Mutual Information based scores,AMI);调整兰德系数(Adjusted Rand Index,ARI);FM 指数(Fowlkes and Mallows Index,FMI).3 个指标都是评价聚类算法性能的外部指标,通过聚类结果与参考数据集的标签比较而获得,这些外部指标度量的结果都在[0,1]之间,指标值越接近1 说明聚类的结果越好.

3.3 检验模型性能

图1 和图2 根据Breast Tissue 数据集的主成分贡献率所选择的平面图,图1 是本文算法在数据集上,两个高贡献率维度的图像,图2 是PSO-FCM 算法,从图中可以明显的对比出来,在相同数据集,相同维度下的本文算法聚类的结果明显优于PSO-FCM,PSO-FCM算法在数据比较集中的区域,对于多个聚类中心的交界处的数据敏感程度低,无法有效的给出数据的准确的聚类中心,相反本文算法面对这类粒子,敏感度高,能够更加有效的且准确的给出聚类中心.粒子各维度之间无差别移动,在多个聚类中心的粒子会被错误的移动到不正确的聚类中心中:本算法对于不同贡献率的空间中,采取相对应的移动权重的能够较低粒子错误移动的概率,说明该策略效果是显著的.

由表2 和表3 中可以看出,本文算法只是在Dermatology 数据集上的AMI 这一个指标上落后KNN,这是因为作为硬聚类算法,随着聚类中心数目的增加,每一个数据只能存在单一的一个聚类结果,不会存在多种可能性,聚类的结果纯度更高.KNN 算法性能很稳定,在随着聚类中心增多,性能反超FCM,PSO-FCM 两个算法,但是综合指标上,本文的算法总体仍是优于FCM,PSO-FCM,KNN 这3 个算法.FCM 采用随机初始的中心,指标随着聚类中心的增多,算法性能下降明显.PSOFCM 采取使用PSO 算法得出的初始中心,明显的发现,综合性能上面性能上优于FCM,但是算法精度提升不高.

图1 PCA-PSO-FCM 高贡献率图

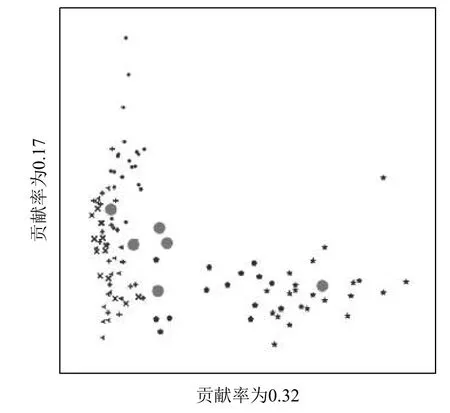
图2 PSO-FCM 高贡献率图

随着各数据集的聚类中心的增加,聚类的问题的复杂化,从表中各指标上,侧面体现本算法面对多个聚类中心的之间的粒子敏感度更高,分辨能力更强.总体上指标上来看,本文算法性能更强,鲁棒性更高,适用面更广.

4 结论与展望

采取PCA 优化的PSO-FCM 算法,通过主贡献率加权的限制,控制粒子各维度上的移动,降低多聚类群交界粒子的敏感性,增强了粒子的搜索能力,降低粒子被不正确粒子群吸入,能够一定程度上,跳出局部最优,有效的弥补了传统PSO-FCM 性能上的不足,增加算法精度,增强算法的鲁棒性,相对于其他算法,在综合指标上面更优,部分指标上有着更好的精度,适用面更广,鲁棒性更强.接下来的工作会将优化算法应用到更多领域.

表2 算法性能表1

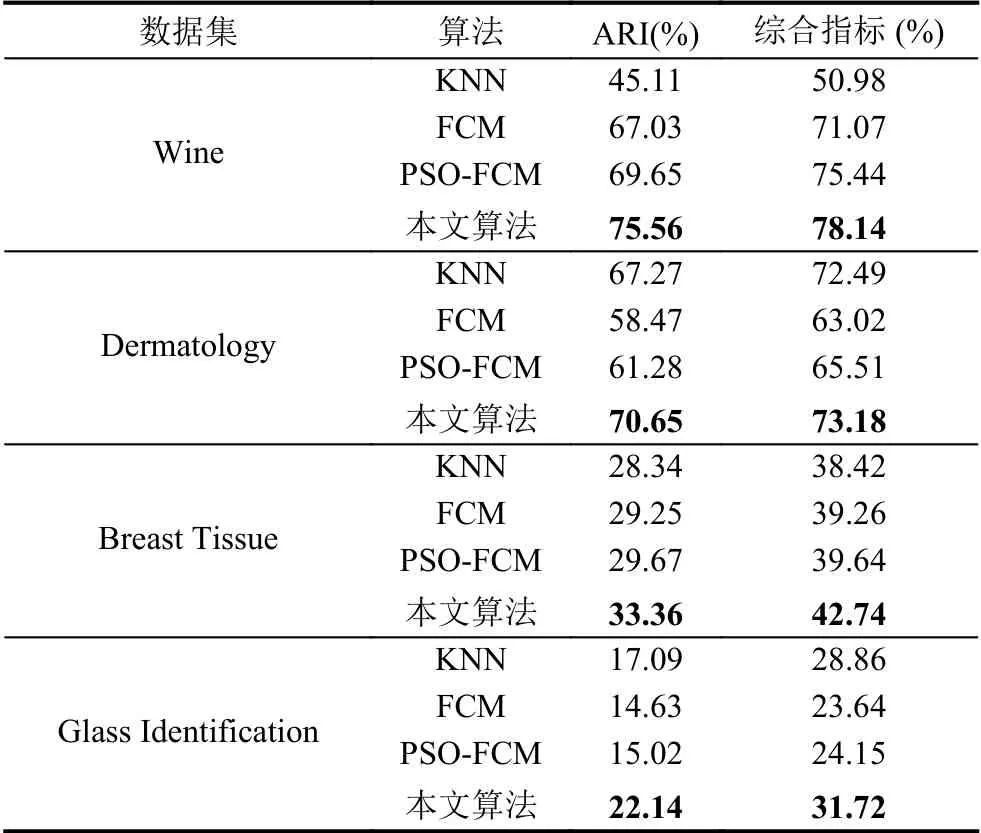
表3 算法性能表2