多通道转杯纺羊毛混色织物的Friele模型

杨瑞华， 王卓， 邓茜茜， 徐亚亚

(江南大学 生态纺织教育部重点实验室，江苏 无锡 214122)

为满足市场发展需求，现代纺织技术不断革新，大量新型纺纱技术应运而生，纱线形式呈现出多样化趋势。在各种新型纱线中，色纺纱线因其独特的外观、丰富的色彩，加之其生产方法，符合人们追求环保、个性时尚的消费理念，深受消费者青睐[1-2]。传统混色纺纱的生产是先在前纺工序对有色纤维进行均匀混合，然后再纺制成纱；三通道转杯纺纱技术是将转杯纺与复合纺纱相结合，把不同颜色的粗纱条同时喂入转杯纺纱系统，并均匀混合，一步成纱，不仅缩短了色纱生产流程，还可小批量、多品种生产，快速应对市场需求[3]。转杯纺作为一种新的纺纱方式，因其流程短、产量高、纤维适应性广，可循环利用废弃的羊毛制品或下脚料，在毛纺领域具有很好的发展前景[4-5]。为将三通道转杯纺纱技术引入毛色纺产品的生产，文中以有色毛纤维为原料，利用三通道转杯纺纱机生产羊毛混色纱线，并研究混色织物的混色规律，为未来三通道转杯毛纺产品在计算机测配色方向的发展提供理论依据。

计算机测配色技术以配色模型理论为依据，对来样进行辅助配色，从而解决工厂配色难、效率低等困难。目前，常用的纤维混色配色模型主要有Kubelka-Munk双常数模型[6-7]、Stearns-Noechel模型[8-9]以及Friele模型[10-11]，其中Friele模型是唯一在光学理论基础上针对色纤维混合特征而提出的配色模型。文中利用Friele模型分别对三通道转杯羊毛混色针织物及梭织物的混色规律进行探究，并分析Friele模型是否适用于三通道转杯毛纺混色织物的测配色。

1 材料与方法

1.1 原料与仪器

1.1.1原料 红、黄、蓝纯色羊毛粗纱，浙江兰宝毛纺集团有限公司生产。

1.1.2仪器 Datacolor 650分光光度仪，美国 Data-color公司制造。

1.2 实验方法

1.2.1纺纱方法 利用多通道转杯纺纱机混与纺一体式的独特纺纱方法，将红、黄、蓝3色羊毛粗纱同时喂入由独立伺服电机控制的给棉罗拉中，通过给棉罗拉的给棉速度控制纤维混色比例，并在转杯纺纱机独有的分梳辊及转杯装置的高速运转下，将喂入的不同颜色的粗纱条进行分梳及均匀混合，纺制出一定比例混合均匀的混色纱线[12]。

1.2.2样品制备 纺制了红、黄、蓝3种纯色纱，并以质量比为10%的变化梯度将3种颜色两两混合纺制混色纱，共30个纱样，分别织成纬编针织平纹织物和梭织斜纹织物，用于求解不同织物结构下的最佳参数σ值。其中纱线线密度为44.85 tex，纬编针织平纹织物的线圈密度为108 个/cm2，梭织斜纹织物的经密为306 根/dm、纬密为192 根/dm。利用红、黄两色纤维混合制成的不同比例混色针织物及梭织物分别如图1和图2所示。由图1和图2可以看出，利用相同纱线不同织造形式织出的织物在颜色及视觉效果上稍有不同，针织物有较明显的色斑效果，而梭织物由于经纬纱交织，弱化了色斑，在纵向上呈条纹效应。

图1 不同混色比例针织物Fig.1 Knitted fabrics of different color blending ratios

图2 不同混色比例梭织物Fig.2 Woven fabrics of different color blending ratios

1.2.3测试方法 织物样本采用分光光度仪测量其各波长下的光谱反射率。测量环境为：D65标准光源，10°视场，30 mm大孔径。为减少测量误差，测量时保证样本不透光，每个样本测量10次，取其平均值，波长取值范围为380～700 nm，取点间隔为10 nm，即每个样本共有33个波长下的光谱反射率值。

2 Friele模型及参数σ计算

当不同颜色的单色纤维根据不同质量比进行混合时，其形成的混色样品反射率与单色纤维的反射率假设存在以下加和关系：

f[Rb(λ)]=∑xif[Ri(λ)]

(1)

式中：Rb(λ)表示波长为λ时混色样品反射率；xi为混色样品中第i组分单色纤维的质量分数，且满足∑xi=1；Ri(λ)表示第i组分单色样品在波长为λ时反射率。

1952年，Friele在加和公式的基础上推出了一个关于反射率的函数式，即Friele模型，具体表示为

f[R(λ)]=e-σ[1-R(λ)]2/2R(λ)

(2)

式中：R(λ)表示波长为λ时的反射率；σ为Friele模型参数。

Friele模型可用于有色纤维的混色研究。 Friele利用松散的羊毛纤维进行混色，推荐模型参数σ值为0.3。由于σ的取值受到纤维种类、混合方式等诸多方面因素的影响，于是许多研究者对σ的取值展开了进一步探讨。PHILIPS等[13]对棉混色纱条的推荐σ值为0.245；沈加加等[14]对条子混色的棉和羊毛混色纱线的推荐σ值分别为0.128，0.093。

由式(2)即可反推出预测样本的反射率

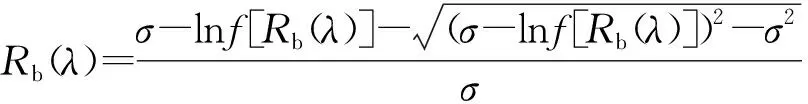
文中通过多通道转杯纺纱机对有色纤维进行混色，并利用赋值法对Friele模型参数σ进行循环赋值(赋值范围为0.001～1，赋值间隔为0.001)，分别求取针织样品和梭织样品平均色差最小时σ的取值作为最佳σ值，从而利用最优参数建立关于多通道转杯毛纺混色织物的Friele模型。文中色差计算均采用CMC(2∶1)色差公式。不同赋值参数下样品平均色差的取值变化如图3所示。

图3 不同σ值对应织物样品平均色差Fig.3 Average color differences of fabric samples with different σ values

由图3可以看出，针织样品和梭织样品的平均色差随着σ值的增大，呈先减小后逐渐增大的趋势；当σ值在0.1～0.2范围内时，样品平均色差达到最小。为清楚地呈现出样本平均色差在0.1～0.2范围内的变化情况，在0.1～0.2区间内作平均色差变化图，具体如图4所示。由图4可以看出，两种织物样品的平均色差在此范围内因σ值的不同变化差异较大。当σ值为0.125时，针织样品的平均色差达到最小；当σ值为0.141时，梭织样品的平均色差达到最小。因此取针织物的Friele模型最优σ值为0.125，梭织物的Friele模型最优σ值为0.141。

图4 σ值在0.1～0.2区间内的织物平均色差Fig.4 Average color differences with the value of σ in the range of 0.1～0.2

3 配方计算

根据求得的最优模型参数，利用全光谱配色法对样本进行配方预测，假设在预测配方下标准样反射率与配色样反射率无限接近，即满足[15]

Rs(λ) ≈Rm(λ)

(4)

式中：Rs(λ)为各波长下标准样反射率，Rm(λ)为各波长下配色样反射率。

由式 (2)可推得

f[Rs(λ)] ≈f[Rm(λ)]

(5)

对于3组分样品配色，由式(1)可得到

f[Rm(λ)]=x1f[R1(λ)]+x2f[R2(λ)]+x3f[R3(λ)]

(6)

设

可得到Fs≈FX

(7)

利用式(7)中的33个线性方程组求解3个未知数，则方程有解，且为多个解，因此利用最小二乘法求方程组的解，即使Δ→0

x2f[R2(λ)]-x3f[R3(λ)]}

解得>X=(FTF)-1FTFs

(8)

利用最小二乘法求解出的预测配方使得匹配样与标准样之间反射率差异最小，但为保证各单色纤维预测配方和为1，需对以上求得的配方进行归一化处理，作为最终的预测配方。

4 预测结果分析

根据求得的预测配方，即可预测混色样关于Friele模型的f[Rb(λ)]，并利用式(3)可以计算出预测混色样的反射率Rb(λ)，根据标准混色样与预测混色样的反射率，计算预测配方下预测样品的色差。

为验证预测配方的准确性，文中在针织样品和梭织样品中分别选取10种不同比例的3色混色样品，利用最优模型参数即式(8)，对样品进行配方预测及预测配方下样品色差计算，其中1～10号验证样品为纬编针织平纹织物，11～20号验证样品为梭织斜纹织物。各样品配色结果见表1和表2。

由表1可知：当σ1=0.125，对针织样本进行配方预测时，有两个样品色差大于1，其他均小于1，平均色差为0.58；当σ2=0.141，对梭织物进行配方预测时，其验证样品的色差在1左右，平均色差为0.83。两种织物的平均色差均小于1，且每个样品的色差均在1个色差单位左右，有效满足了行业内人眼识别的色差要求，预测效果相对较好，说明Friele理论能够较好地应用于多通道转杯毛纺混色织物的纤维混色配比及颜色预测的研究。

5 结语

文中将Friele模型应用于三通道转杯羊毛混色织物的混色规律研究，利用赋值迭代法计算出适用于纬编针织平纹织物的模型参数σ为0.125，适用于梭织斜纹织物的模型参数σ为0.141。将求出的模型参数进行配色，并计算色差，结果显示：样品色差均在1左右，平均色差小于1，满足配色要求，预测效果相对较好。

多通道转杯纺纱技术能够将混色与纺纱一体化生产，在未来色纺领域具有较好的发展前景。计算机测配色技术是未来色纺纱发展的必然趋势，将多通道转杯纺纱技术与配色计算技术相结合，可为未来多通道转杯纺纯羊毛混色织物计算机配色软件的开发及应用提供一定的理论依据。