基于模拟轮轨力的GJ-3型扣件性能仿真分析

王煜晖， 王安斌， 刘 浪

(上海工程技术大学 城市轨道交通学院， 上海 201620)

0 引 言

近年来国内各城市的轨道交通均已采用了大量的减振措施，需要减振线路段都需要安装减振扣件。GJ-3型扣件是比较常见的一种减振扣件，其主要减振方式是在列车通过时，列车对钢轨施加轮轨力，轮轨力从钢轨传递到整个扣件系统，扣件系统靠自身的两层橡胶垫来吸收轮轨力所带来的冲击，起到减振的作用。目前国内对该扣件系统也有一定的研究，王平等人以国内某GJ-3型扣件线路段的环境噪声为研究对象，使用响度分析方式对噪声水平进行评价[1]；王志强等人现场测试GJ-3型扣件系统的动态特性和运营条件下的轨道变形及振动水平，得到了该扣件的减振效果[2]；王蕊等人在GJ-3型扣件某线路段现场实测了数据，进行了时域和频域的分析，来研究该扣件的减振效果[3]。

综上所述，目前研究都是针对GJ-3型扣件在线路上整体使用效果的实验研究，缺乏单独对GJ-3型扣件综合性能的仿真研究，本文首先使用Solidworks软件建立GJ-3型扣件实体模型,再利用ABAQUS软件建立GJ-3型扣件有限元模型，从仿真的基础上对GJ-3型扣件进行性能分析，为城市轨道交通减振扣件选择提供参考。

1 GJ-3型扣件系统结构

GJ-3型扣件是轨道交通工程中的一种能将减振、降噪性能合二为一的先进的结构形式, 其减振的主要方式是由双层非线型减振降噪结构完成的[4]。GJ-3型扣件主要由钢轨、上层铁垫板、下层铁垫板、轨下橡胶垫、中间橡胶垫板、尼龙套和调高垫板组成。GJ-3型扣件没有使用传统的w型弹条，而是使用了e型弹条，而且相较与一般的铁路系统扣件，GJ-3型扣件使用了两层橡胶垫板。通过这样的设置，GJ-3型扣件可以获得比较低的垂向刚度，很好地起到扣件的减振作用，从而减少了轮轨之间的振动冲击向轨下基础传播，控制了道床、地基、隧道壁以及地面的振动。

2 扣件有限元模型建立及约束参数设置

为了对GJ-3型扣件的力学性能作出评价,用ABAQUS软件建立了该扣件结构力学分析计算的有限元模型,分别计算了扣件结构的变形、应力和模态。

2.1 有限元模型的建立

为了验证仿真结果的正确性，了解真实条件下GJ-3型扣件的性能效果，选择对单个GJ-3型扣件模型建模。首先，利用Solidworks 软件按照实际尺寸建立各部件的三维模型，对结构适当的简化；其次，导入ABAQUS 软件中按照实际位置装配，得到GJ-3型扣件的有限元模型，用ABAQUS软件建立扣件结构力学分析计算的有限元模型如图1所示。该模型共有119 140个结点，437 633个单元，模型中的所有参数采用国际单位制。

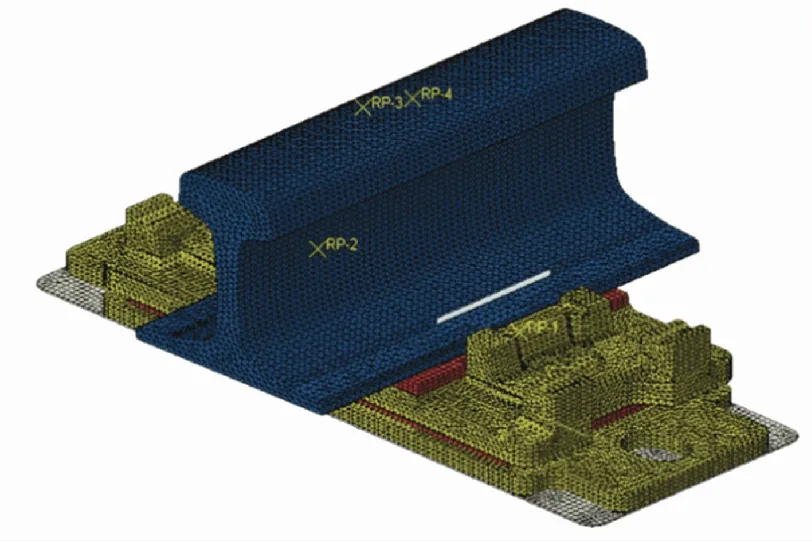
图1 扣件结构有限元模型图

2.2 设置单元类型

模型中有二种单元：梁单元用来模拟弹条(等效为线性弹簧，直接垂向作用于轨角，单个初始压力9 KN，弹簧刚度1 KN/mm)；实体单元用来模拟钢轨、上层铁垫板、下层铁垫板、轨下橡胶垫、中间橡胶垫板、尼龙套和调高垫板等构件。

2.3 设置材料常数

结构中共有6种材料，其中上层铁垫板和下层铁垫板的材料为球墨铸铁，调高垫板材料为聚乙烯， GJ-3型扣件模型其材料参数见表1。

2.4 设置约束

调高垫板下底面所有结点的3个方向的平动自由度全约束，钢轨和轨下橡胶弹性垫板、轨下橡胶垫和上层铁垫板、上层铁垫板和中间橡胶垫板，中间橡胶垫板和调高垫板之间都采用面对面接触[5-6]。

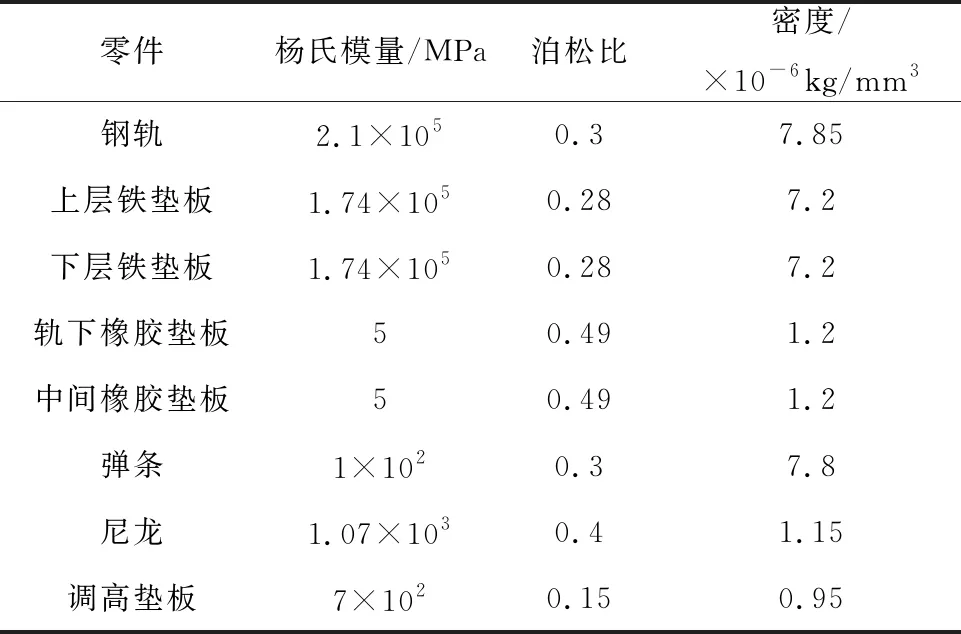
表1 主要部件材料参数

2.5 模拟轮轨力

为了模拟轮轨力，按照列车通过的实际情况，向GJ-3型扣件系统施加载荷，轨角施加水平推力(x向)15 KN，竖直施加压力(z向)30 KN，水平力与竖直压力按线性分布施加。

3 GJ-3型扣件系统性能仿真分析

3.1 仿真静刚度

有研究表明：在条件允许下，扣件垂向刚度越低，对减振降噪越有利，而垂向静刚度是橡胶减振扣件的重要性能指标之一[7]。下面对单个GJ-3型扣件进行静力学仿真，验证其横向刚度和竖向刚度是否与实际情况相符。

结构的横向(x向)变形如图2所示。横向最大位移为2.476 mm，钢轨顶面分别位于4个象限的4个角点的横向位移分别为2.352 mm、2.352 mm、2.370 mm、2.370 mm，钢轨顶面中心的横向位移为2.451 mm。结构的竖向(y向)变形如图3所示，竖向最大位移分别为-1.647 mm，钢轨顶面分别位于4个象限的4个角点的竖向位移分别为-0.383 mm、-0.383 mm、-1.233 mm、-1.233 mm，钢轨顶面中心的竖向位移为-0.807 mm。根据试验要求，求得仿真横向刚度为6.12 kN/mm，仿真垂向刚度为18.21 kN/mm。仿真得到的横向刚度和竖向刚度在中等减振扣件设计刚度的范围内，所以材料设置合理，模型正确。

3.2 强度分析计算

为了探究在模拟轮轨力的情况下，GJ-3型扣件内部上层铁垫板和下层铁垫板的受力情况，在仿真结果中对上层铁垫板和下层铁垫板单独分析。仿真应力情况如图4和图5所示。

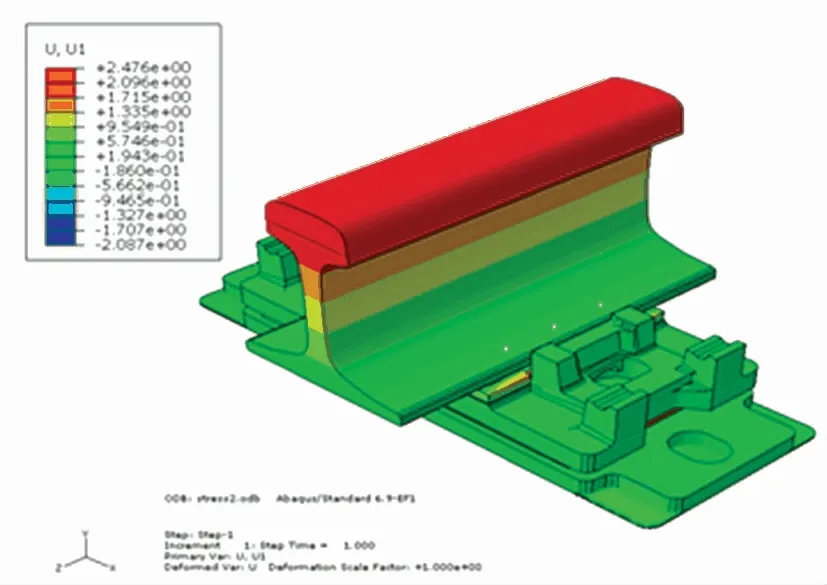
图2 结构横向变形图

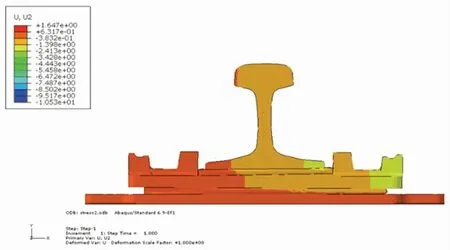
图3 结构竖向变形图

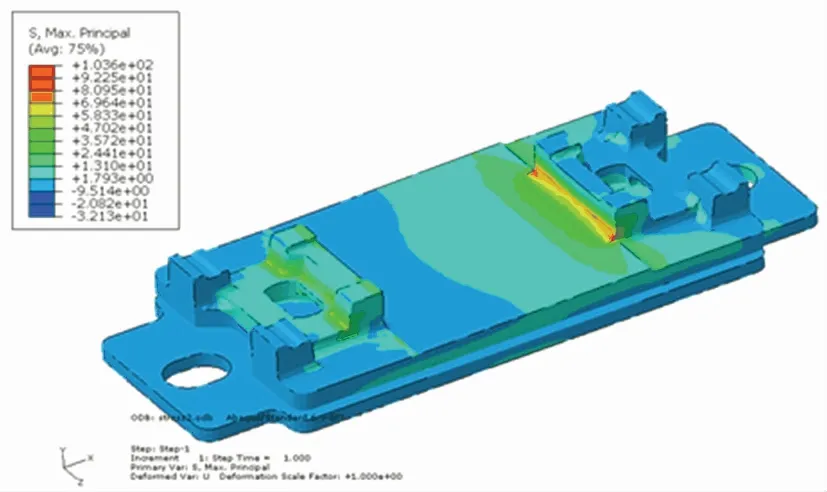
图4 上层铁垫板应力图

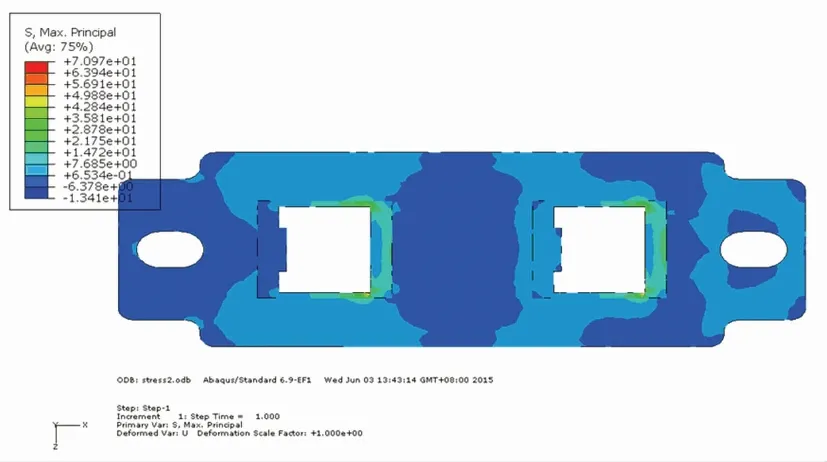
图5 下层铁垫板应力图

由仿真结果可知，上层铁垫板的最大综合应力为103.6 MPa，在弹条座底部。下层铁垫板的最大综合应力为71.0 MPa,在大方孔角部。根据上述仿真分析结果得出的上层铁垫板和下层铁垫板的应力分别为103.6 MPa、71.0 MPa，均能满足强度要求。

3.3 模态分析计算

在模拟轮轨力的情况下，对强度分析的模型继续做模态分析计算，分析了结构的前25阶固有频率和振型，钢轨变化比较大的几阶振型如图6～图10所示。

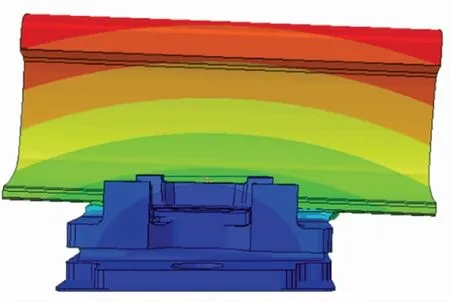
图6 1阶振型图

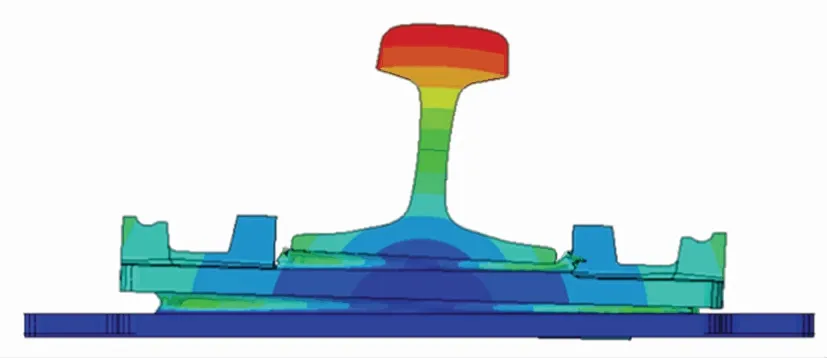
图7 2阶振型图

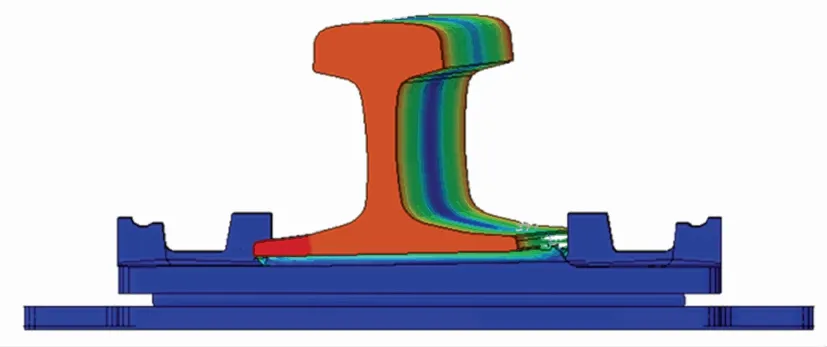
图8 3阶振型图

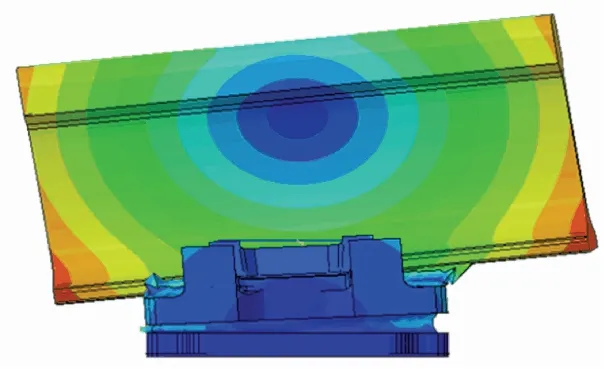
图9 4阶振型图

图10 5阶振型图

对前25阶模态振型结果进行统计，见表2。

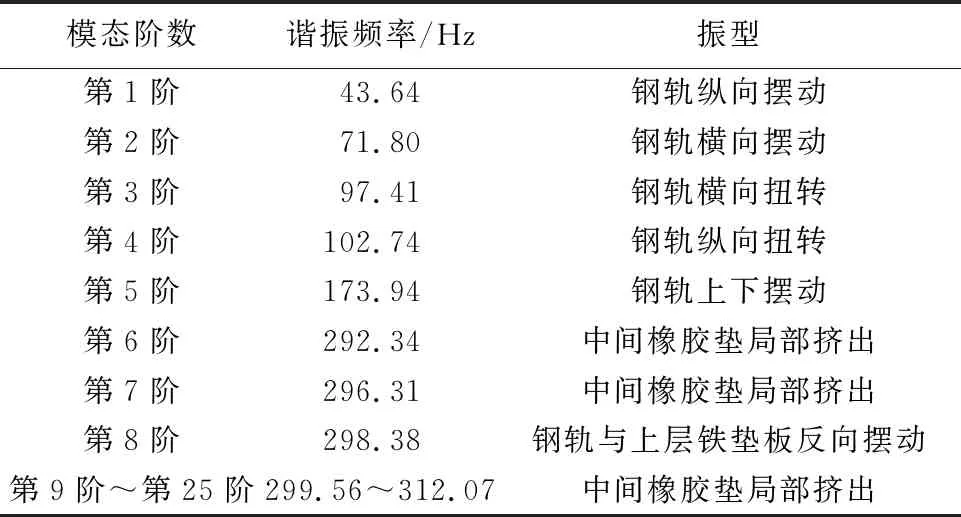
表2 前25阶模态振型结果

根据上述仿真分析，看出谐振频率为第1阶、第2阶时，钢轨发生横纵向摆动；谐振频率为第3阶、第4阶时，钢轨发生横纵向扭转；第五阶时，钢轨发生上下摆动；第八阶时，钢轨与上层铁垫板反向摆动；其余阶数为中间橡胶垫局部挤出。

故当谐振频率为43.64～173.94 Hz和298.38 Hz时，钢轨会发生较大的变形，所以属于较为危险的频率，实际情况中应当考虑。

3.4 列车激振频率计算

列车在行驶过程中，扣件需要避开的主要频率段为：

(1)车轮经过轨道扣件的频率；

(2)车轴经过轨道扣件的频率；

(3)转向架经过轨道扣件的频率。

3个频率在车速120 Km/h以及140 Km/h时激励频率见表3。

表3 不同车速下的轨道特征频率

有限元模态分析可看成求解具有有限个自由度的线弹性系统运动方程。在分析过程中，对于弹条阻尼假设以材料阻尼为主，采用复刚度的虚部来表述对其模态频率及振型的影响，其矩阵表达式为[8]：

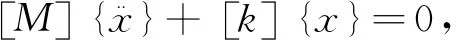
(1)

式中：M为弹条的质量矩阵；K为复刚度矩阵。

复模态分析的目的是计算有阻尼系统的模态，并用于确定所研究对象的结构稳定性[9]。其分析实质是将线性振动微分方程组中的物理坐标变换为模态坐标，使得方程组解耦，则方程可改写为式(2)[10]:

(p2M+K)φ=0,

(2)

式中：p为特征值;φ为对应的特征向量。

在实模态分析基础上，通过在实模态投影生成的子空间上形成复特征值问题，并使用海森伯格缩减方法提取复模态参数。将矩阵投影到由n个实模态特征向量组成的空间上[11]，可得式(3)和式(4)：

M*=[φ1…φn]TM[φ1…φn],

(3)

K*=[φ1…φn]TK[φ1…φn].

(4)

因此方程的复特征值和复特征向量可分别表示为式(5)和式(6)：

p=α+βi,

(5)

φ=[φ1…φn]Tφ*.

(6)

求解可得n个弹条的固有频率wi，{xi}为对应的模态振型，其中i=1，2，3…n。

根据上述有限元计算理论，结合模态分析计算结果，计算3个频率在车速120 Km/h以及140 Km/h时激励频率，根据模态分析计算结果，扣件的各阶固有频率均远离列车的激振频率，即扣件不会和列车的激励产生共振。

4 结束语

在建立GJ-3型扣件的基础上，在模拟轮轨力的情况下对其进行强度分析与模态分析来进行研究，得出以下结论：

(1)根据GJ-3型扣件实际尺寸建立出扣件的有限元模型，通过力学仿真得到扣件的仿真横向刚度为6.12 kN/mm，仿真垂向刚度为18.21 kN/mm，在设计刚度范围内，为仿真计算提供可靠的理论模型。

(2)仿真模拟轮轨力的强度分析结果得出，上层铁垫板和下层铁垫板的应力分别为103.6 MPa、71.0 MPa，均能满足强度要求。

(3)仿真模拟轮轨力的模态分析结果得出，当谐振频率为43.64～173.94 Hz和298.38 Hz时，钢轨会发生较大的变形，所以属于较为危险的频率，实际情况中应当考虑。

(4)根据列车激振频率计算结果得出，扣件的各阶固有频率均远离列车的激振频率，即扣件不会和列车的激励产生共振。