基于模拟退火算法的压电薄板振动抑制研究

邹光浩， 郭 辉

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

0 引 言

薄板在工程领域中有着广泛的应用，人们对其使用过程中产生的振动加以利用，发明了振动压路机、测试振动台等。但薄板振动也会为生产生活带来诸多问题，比如会缩短机械的使用寿命、产生噪声、降低使用者舒适度等。因此，在薄板的实际工程应用中，要进行振动控制。减振方法通常分为主动控制与被动控制。压电分流阻尼技术属于被动控制方法中的一种，与主动控制相比，其控制系统较为简单，易于实现。该技术通过压电作动器把振动结构的机械能转换为电能，通过分流电路中的电阻把电能消耗掉，从而减少系统的总能量，达到抑制结构振动的目的。压电分流阻尼技术具有结构简单，成本低和容易实现的特点，已经在工程实践当中有一定的应用[1]。

分流阻尼电路的电阻、电感值以及压电片的布置，对其抑振效果起到了重要作用。

(1)压电片的布置位置直接影响其受到激励后产生的电能大小;

(2)分流电路中电路参数的大小决定了机械能被转化并消耗的能力。

针对参数优化，Hagood和Von Flotow[2]研究了电阻R以及电阻R和电感L串联的两种分支电路形式，推导出了参数优化公式并且建立了被控结构为单自由度系统时的数学模型；WU[3]在大量前人研究基础上，延伸推导出了并联RL电路的参数优化表达式，并且证明了并联电路同样可以控制结构产生的振动与噪声；杨志春教授[4]对压电分流阻尼技术的机电耦合系数进行了研究，找到了机电耦合系数对压电分流阻尼系统减振效果的影响规律；毛崎波教授[5]利用四边固支的薄板模型，对比了3种不同分流电路的减振效果，证明在达到最优参数时，3种分流电路都可以起到很好的减振效果。

在计算电路参数时，前人对于传递函数法与极点配置法的研究已经较为成熟。其中，传递函数法是建立单自由度弹簧等效系统及其位移传递函数。利用传递函数优化方法，降低传递函数幅值。极点配置法是建立机电耦合模型，由系统阻抗公式出发，并进行展开，从系统位移衰减入手，用极点与虚轴之间距离代表衰减量，以增大衰减量为目标。但利用这二种方法仅仅可以解决单一频率处的振动问题，并不能对特定频率范围内的多个频率处的振动进行控制。本文运用模拟退火算法对薄板结构的分流电路参数进行优化，对0-500 Hz内的结构振动幅值进行控制与分析。并与传递函数方法、极点配置方法的优化结果进行对比，体现了此方法对于多点振动控制的有效性。

1 动力学基本方程

1.1 薄板单元分析

本文研究对象是外形规则的矩形薄板，因而在有限元建模时宜选用矩形单元。为了较好地反映真实的变形情况，在相邻单元在公共节点处除了应有相同的挠度之外，还应有沿x及y向斜率(倾角)的连续性。因此，在任意节点处有3个节点位移分量：挠度、法线绕x轴及y轴的转角[5]，如图1所示。

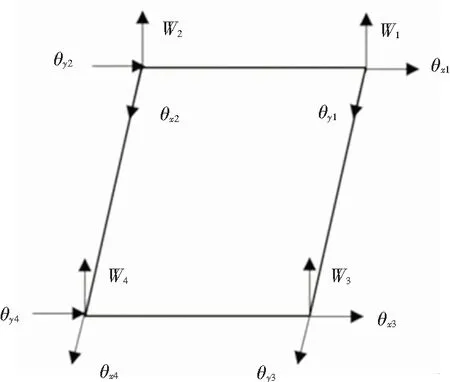
图1 单元薄板自由度示意图

一个单元薄板对应12个自由度，每个节点处对应各自的挠度与转角，所以单元位移可假设成包含12个常数的多项式，通过求解可将挠度利用节点位移表示[6-7]：

w=[N]{η}.

(1)

其中：

[N]=[N1,Nx1,Ny1,N2,Nx2,Ny2,N3,Nx3,Ny3,N4,Nx4,Ny4],

{η}={w1,θx1,θy1;w2,θx2,θy2;w3,θx3,θy3;w4,θx4,θy4}T.

薄板中面内的点在Z方向位移W，称为挠度。当挠度小于或者等于薄板厚度的五分之一时，可利用基尔霍夫假设，即：

(2)

1.2 压电薄板分析

压电元件在建模的过程中作如下假设：忽略压电元件的转动惯量；压电元件的尺寸远小于薄板的相应尺寸；薄板的水平方向变形与垂直方向变形相比忽略不计。

对于线性压电材料，根据自变量的不同，一共有4类压电方程。现根据第2类压电方程，取压电层的极化方向为z向，并在z方向施加外加电场，则压电体的本(结)构方程可简化为[8-9]：

(3)

其中，Dz、Ez分别为Z向电位移及Z向外加电场强度；[CE]、[e]、{ε}分别为压电材料的弹性常数矩阵、压电常数矩阵和压电层厚度方向的介电常数；{σ}、{ε}分别为应力和应变向量。

2 动力学微分方程

设Vp是PZT板的单元体积；Vb是薄板单元体积；ρp是PZT板密度；ρb是薄板密度；hp是PZT板厚；Ve是PZT板上产生的电压。单元动能(仅考虑结构在z方向上的动能)由薄板动能与PZT板的动能组成：

(4)

(5)

单元势能由薄板应变能、PZT薄板应变能以及PZT薄板电势能组成：

(6)

(7)

(8)

薄板受到单位力p,如图2所示，与薄板法线方向成θ，外力作用下薄板单位面积受力f=pcosθ。则外力做功：

WF=∬AwfdA.

(9)

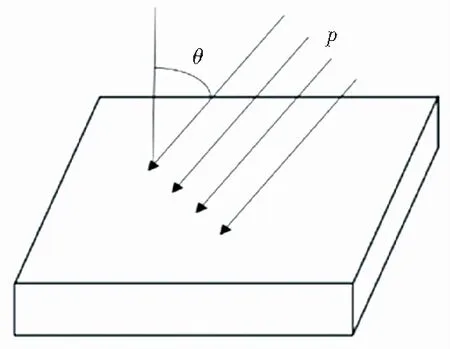
图2 薄板受力示意图

根据Hamiton原理，薄板压电片单元系统的有限元方程为：

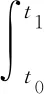
(10)

将以上式子带入后得：

∬A[N]{η}fdA]dt=0.

(11)

将上式对{η}进行变分运算，再由δ{η}得任意性，可推得单元在仅受外加平面载荷时的方程：

(12)

其中，

[F]=∬A[N]fdA.

再将阻尼项加入：

(13)

综合上述得：

(14)

假设电位移沿着压电元件表面均匀分布，得到[9]：

(15)

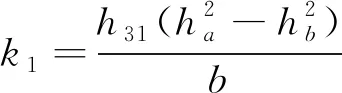
选取RL串联分流电路，其阻抗表示为Z=R+Ls，并将上式入(14)，得到针对第n阶模态控制时的方程式为：

ηn(s)=F.

(16)

式中，mb、mp分别为薄板与压电片的模态质量；kb、kp分别为薄板与压电片的模态刚度；c为模态阻尼。由式(16)可推导出函数G(s)，代表系统的被动阻尼特性，在力F的作用下，得到的系统某点处位移η(s)。G越小则表明系统的输出位移越小，过程中消耗的能量越多，系统位移响应振幅衰减越快，减振效果更好。因此对分流电路的阻尼参数进行优化，进而达到更好的减振的目的。

(17)

3 分流电路的参数优化

通过对电路参数的优化，从而使压电分流阻尼电路转化更多的热能。对于不同的优化目标可将优化方法分为：传递函数法与极点配置法。本文将运用模拟退火算法，对分流电路的参数进行优化。通过仿真实验验证其有效性，并将其与传递函数优化方法、极点配置优化方法设计的分流电路的应用效果进行对比[10-11]。

3.1 建立优化模型

在垂直于薄板平面的方向上施加力F，在对角点处得到输出位移，如图3所示，通过式(18)得到输出点处垂直位移与外力F之间的传递函数。考虑压电分流电路对整体结构的影响，建立线性规范模型并以A(R,L)表示，以传递函数最小值作为目标函数，求得相对应的最优电阻值Ropt与最优电感值Lopt，即：

(18)

(19)

约束条件为：R>0，L>0。

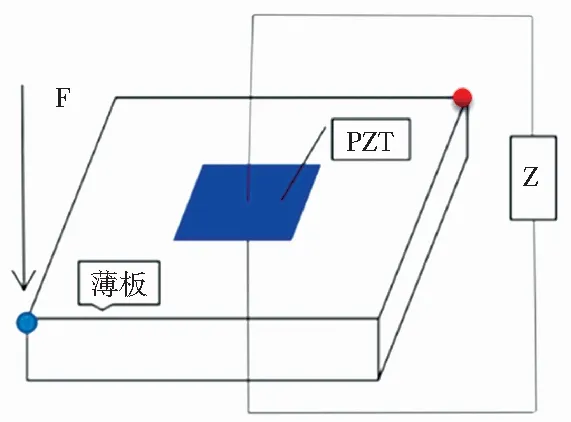
图3 压电薄板结构示意图

3.2 运用算法对函数进行优化

模拟退火算法的思想源于固体退火过程。将固体加热至足够高的温度，再等其缓慢冷却，同时内能趋于最小。其中，缓慢冷却即随机解，内能大小即为目标函数，将随机解不断进行扰动，并以一定概率接受解，使目标函数值不断优化，最终趋于最优。模拟退火算法步骤描述如下[12]：

步骤1设S为初始状态，初始温度T0=90 ℃，终止温度T1=89 ℃，降温速率q=0.98。

步骤2产生新解S’。

步骤3按照一定方式进行降温，计算温差Δt。

步骤4利用Metropolis准则进行判断：计算S的增量df=f(S)一f(S’)，若df<0，则将S’视为新的当前解；否则按照S的接受概率exp(-df/Δt)接受S。

步骤5直到退火温度小于设定温度时，输出结果，停止计算。

步骤6利用降温速率q=0.98进行降温，即T=0.98*T0。然后跳回到步骤2，直到T小于终止温度。

其主要实现流程如图4[13]所示：

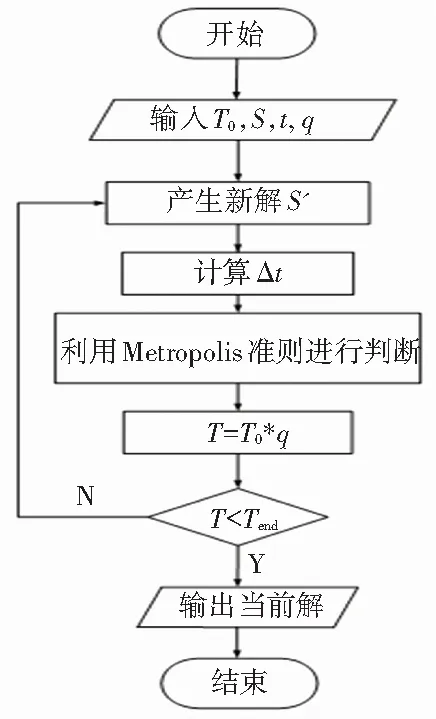
图4 模拟退火算法流程图

3.3 数值算例

3.3.1 模拟退火算法对分流电路参数优化

本文被控对象是压电—薄板结构，薄板大小为400×400×2 mm3，材料为铝。仿真利用Comsol Multiphysics对其整个结构进行特征频率分析，得到前四阶模态阵型如图5所示。

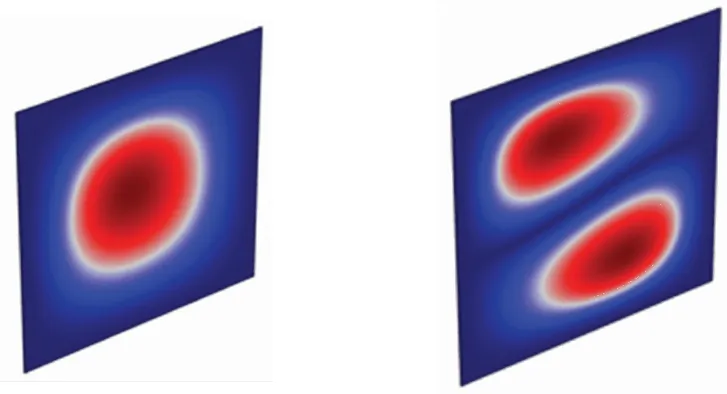
(a) 55.815 Hz (b)113.96 Hz

(c) 113.97 Hz (d) 168.25 Hz

由前四阶模态分析可知，振幅最大的位置处于薄板中心，所以将压电片粘贴在薄板正中心，并与阻抗大小为Z的RL串联分流电路相连接如图3所示，压电片规格为50×50×1 mm3。

在薄板的左下角施加固定激励，方向垂直于薄板平面，令F的对角点作为输出点，输出垂直于薄板方向的位移。利用输入与输出位移，得到薄板的位移传递函数。接下来利用模拟退火算法对函数进行优化。在规定的退火时间内，通过输入不同电阻、电感值可以得到各自对应不同的传递函数。施加相同的激励，对输出的不同结果进行比较，这里以10-500 Hz范围内输出振幅的期望值进行比较，选择期望值最小时的结果为最优值,如图6所示。运用模拟退火算法获得最优电感为：9.5 H，最优电阻为3 065 Ω。

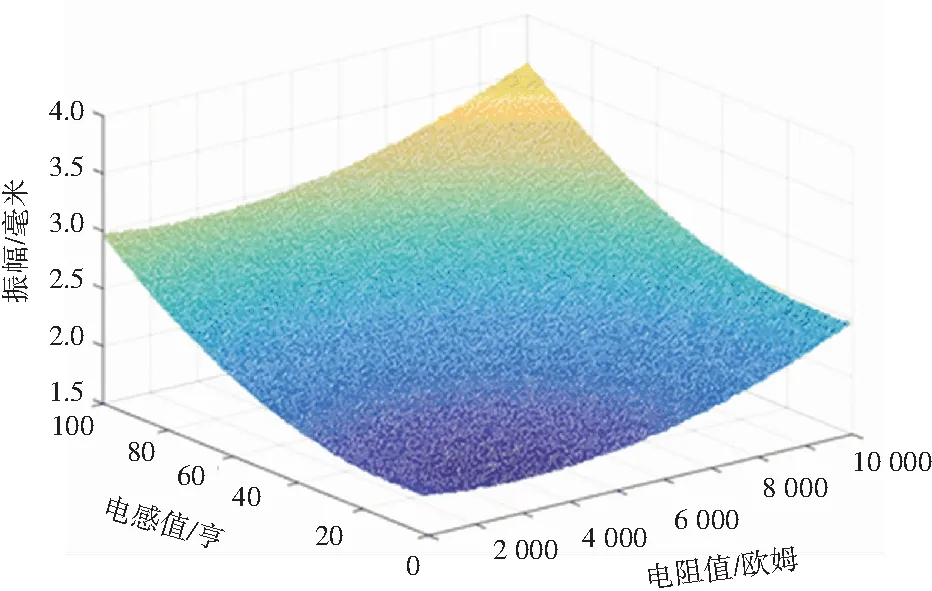
图6 不同R与L条件下，振幅在不同频率下的期望值

为了验证参数优化方法的效果，利用3.2节推导的压电—薄板结构进行数值仿真计算，部分参数见表1。

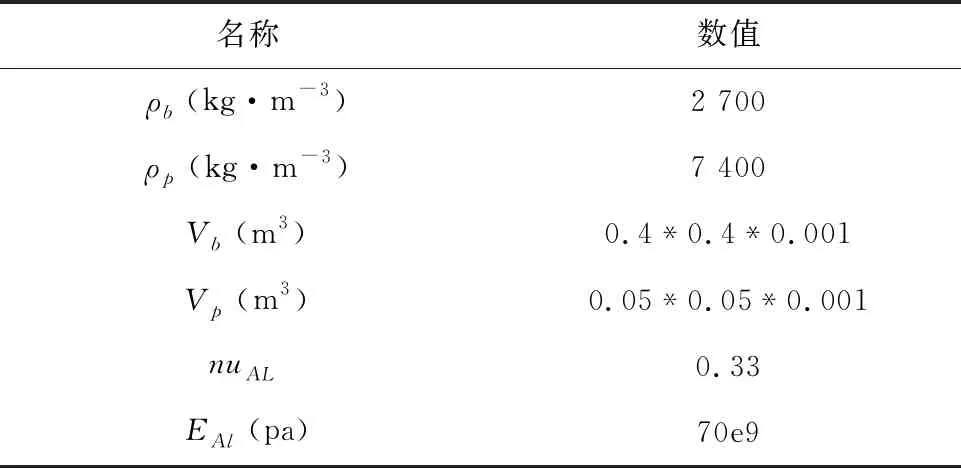
表1 压电片(p)与薄板(b)相关参数

图7是压电—薄板结构在无外接分流电路情况下，与带有优化后的分流电路情况下输出点振动位移变化曲线。由图7可知，在10-500 Hz的低频范围内，当添加分流电路时，输出点处的薄板振动位移小于无分流电路时。具体来看，在振动位移的峰值频率451 Hz处该点的幅值降低了1倍。由此说明，模拟退火算法优化后的压电分流阻尼系统，可以在中低频段内有效的降低薄板上的振动幅值。即表明在中低频段内，通过压电分流阻尼技术抑制了薄板的振动。

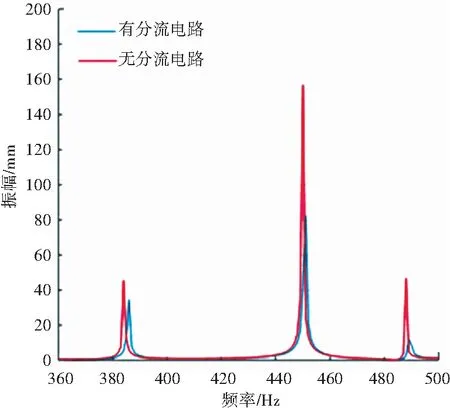
图7 薄板上指定点振动幅值曲线对比

3.3.2 不同参数计算方法的减振效果对比分析

对分流电路参数的选择及优化，可以使分流阻尼电路达到最佳的振动抑制效果。对于不同的优化目标可以将其优化方法分为：使系统传递函数最小化和使衰减系数最大化。前者是传递函数优化方法，后者属于极点配置方法。WU[3]、Park[14]等人对RL串联、并联以及RL-C并联的电路参数进行优化；柳[15]等人对串联、并联分流电路参数进行了计算并验证了其减振效果。运用不同的方法对其进行优化，会产生不同程度的减振效果。因此，对模拟退火算法、传递函数法、极点配置法等，对整体结构的抑振效果进行对比。

利用传递函数法得到，RL串联电路的优化参数公式：

(20)

(21)

利用极点配置法得到，RL串联分流电路优化参数公式：

(22)

(23)

由于前四阶固有频率相隔较宽，针对其中一阶固有频率进行控制时，可以将其看成一个单自由度系统。将压电片依旧粘贴于薄板中心位置，压电片的固有电容Cp=240 nF。在计算机电耦合系数k时，一般的压电振子具有损耗，在压电振子谐振时，会产生最小阻抗频率fm、最大阻抗频率fn、谐振频率fr、反谐振频率fa、串联谐振频率fs、并联谐振频率fp6个不同频率。在进行一级近似之后得到：

fs=fm=fr，fp=fn=fa.

(24)

表2 不同优化方法下分流电路参数

利用Comsol Multiphysics对其结构进行仿真实验分析。由图8可知，3种优化方法得到的振幅曲线，振动趋势基本相同，只是在146 Hz、190 Hz、217 Hz、386 Hz、451 Hz、490 Hz处振幅值略有不同。分析如下：如图9所示，在451 Hz处，前两种优化方法振动幅值相差7 mm，与图7无分流电路的振幅相比，振幅减少约30%。利用模拟退火算法优化后的振幅相比传递函数法与极点配置法分别减少了16.3%和10.6%，减振效果更明显。如图10所示，在146 Hz处，运用传递函数法比极点配置法振幅要低0.6 mm。运用算法优化后，相比较前两种优化方法，振幅分别降低了10.1%、11.7%。3种优化方法相比，运用模拟退火算法优化后的分流阻尼电路，其减振能力更佳。如图11所示，在190 Hz处，运用极点配置法比传递函数法振幅低0.4 mm，与模拟退火算法优化后相比，振幅分别高出11.3%、26.08%。

综上所述，通过对薄板振动幅值数据的分析可以说明：模拟退火算法对于分流电路参数优化的有效性与合理性，并且通过此方法优化后的分流阻尼电路，对振动的控制效果更佳。

图8 同一模型3种优化方法振幅对比

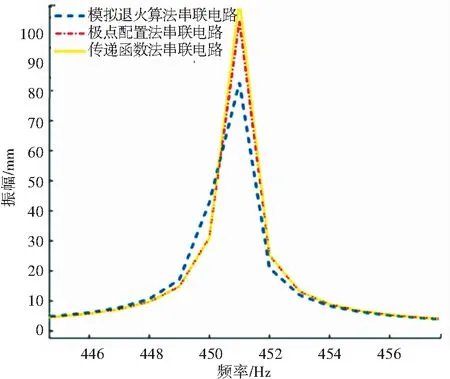
图9 3种优化方法在451 Hz处振幅对比

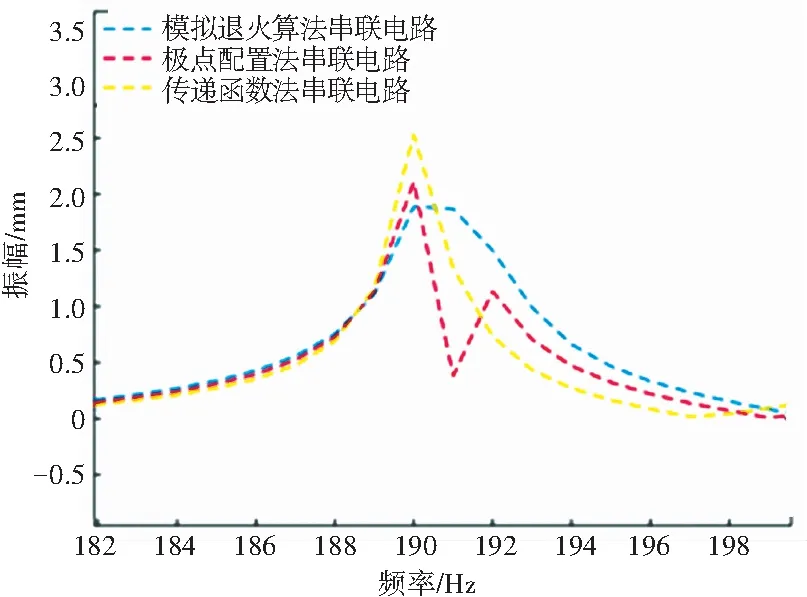
图11 3种优化方法在190 Hz处振幅对比

4 结束语

本文建立了带有压电分流阻尼电路的压电—薄板结构的动力学基本方程，推导出位移传递函数并建立相应的目标函数及优化模型。利用模拟退火算法对电阻、电感值进行选择，得到振幅最小的结果，从而获得最优电感值与电阻值。通过有、无分流电路的仿真实验，验证了模拟退火算法的有效性。最后将模拟退火算法与传递函数法、极点配置法3种方法的减振效果进行对比。结果显示，运用3种方法均可有效降低振幅，从而验证了模拟退火算法对于分流电路参数优化的可靠性。