网联车辆并线预测与巡航控制的研究*

张 涛，邹 渊，张旭东，王文伟

（1.北京理工大学机械与车辆学院，北京 100081； 2.北京电动车辆协同创新中心，北京 100081）

前言

自适应巡航控制（adaptive cruise control，ACC）［1］作为高级驾驶辅助系统（advanced driver assistant system，ADAS）的典型应用之一，利用车载雷达和相机获知前方车辆信息，辅助驾驶员对主车进行控制，有效地提升了行驶的舒适性和安全性。但受限于传感器有限的感应范围和较少的信息量，行驶的安全水准还有待提高。近年来，随着信息通信、计算机和人工智能等技术的发展，智能网联车辆成为新的研究热点，通过车对车（vehicle-to-vehicle，V2V）无线通信［2］，驾驶员或自动驾驶的车辆可获取视野内外更多车辆的多维度信号（包括速度、加速度、航向角、转向盘转角、GPS坐标、车辆尺寸等），为大幅提升车辆安全性提供更大空间［3］。通过网联通信构建协同行驶的车辆队列，被称为协同自适应巡航控制（cooperative adaptive cruise control，CACC），与ACC相比，CACC在避免碰撞冲突和增大交通流量上潜力更大，但仍然存在许多挑战需要解决。例如，网联CACC亟需能够预测其他车辆的车道变换行为［4］。当邻车道车辆在主车前方突然切入换道时，稳定行驶队列中的车辆必须执行紧急制动，而这种紧急制动反应非常危险，可能导致严重的碰撞。因此，预测和适当的提前反应是提升行驶安全最具挑战性的任务之一。

车辆的每次换道行为都对应着车辆状态参数的改变（转向盘转角、车速、航向角等），然而不同的操纵行为（换道、直行）所产出的状态参数可能部分相似［5］。因此，需要一种可靠的方法来基于其车辆状态参数属性来区分不同的驾驶操纵行为。近年来，机器学习技术的发展对基于时序数据的预测提供了新的解决思路和工具，常见的机器学习驾驶员行为建模研究包括基于支持向量机、相关向量机（SVM、RVM）［6-7］和神经网络（NN）［8］等分类方法来识别车辆的行为。另一类主要的建模方案，如隐马尔可夫模型（HMM）［9-10］和动态贝叶斯网络（DBNs）［11］等，利用驾驶行为的历史时间序列数据构建一种因果预测框架，以便找到下一个最有可能的驾驶动机。其中，文献［6］中利用相关向量机（RVM）模型对换道过程参数进行估计，并利用多项式对换道轨迹拟合，将拟合轨迹与可接受安全域面积的比值作为预警参数，用于对换道的安全性进行评估；文献［7］中提出基于雷达采集的旁车横纵向运动信息，基于支持向量机（SVM）构造旁车并线意图识别器，由于雷达采集数据的准确性较低，识别器对干扰信息的识别效果不佳；文献［8］中基于车辆历史运动行为。采用前馈神经网络预测车辆的行驶轨迹；文献［9］和文献［10］中在驾驶员操作过程中，将车辆可观察时间序列行为与未观察到的驾驶员意图序列相关联，根据当前状态预测下一步行为；文献［11］中提出用于识别特殊的高速公路驾驶操作方法，在4个层次上模拟不同的驾驶操纵作为车与车道线、车与车之间的关系。时序预测方法有多种，上述方法能够根据驾驶员的历史行为预测驾驶员不同阶段未来的行为，但是预测过程没有时间和空间限制，不易于在实车应用，且未将预测的行为数据转化引入主车的动态跟车策略中。

针对上述问题，本文中采用一种基于学习的行为预测建模方法，利用非线性自回归（nonlinear autoregressive，NAR）神经网络对实际行驶工况下的旁车道车辆并线数据样本进行学习，通过迭代循环预测算法实现特定时间与空间约束下的车道变换预测，并将预测的横向轨迹转化为切入概率值，构建考虑旁车切入概率的跟车策略，用于CACC控制器提升网联车辆的行驶主动安全性。

1 系统描述与数据采集

旁车并线切入的场景如图1所示，相关参数含义见表1。队列内直接受可疑车辆（旁车）切入影响的车被称为主车，在主车辆前方最近的车辆被称为前车，本文中仅讨论旁车切入后影响的主车道中最小两车系统，未对CACC网联队列系统中其他遥远车辆进行分析。划定主车正前方的区域为危险碰撞区，碰撞区域双侧的一定范围为监视区域，碰撞区域的大小与CACC系统设计的跟车距离策略及车辆尺寸有关。

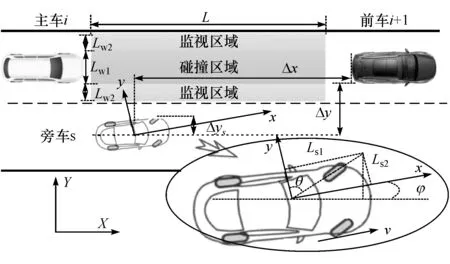
图1 旁车并线切入场景与区域参数示意图

表1 切入区域参数含义

网联车辆跟车策略的目标是引导主车与前车之间保持相对的安全距离与车速，常用跟车距离模型为：固定跟车距离模型、固定跟车时距模型和非线性间距模型等［12-13］，式（1）为固定车间时距模型：

式中：ddes，i为主车期望的跟车距离；h为固定的车间时距；vi为主车的车速；d0，i为设计的主车停车安全距离。碰撞区域范围与跟车距离模型有关，如图1所示，区域的横向尺寸Lw1与主车的宽度相同，纵向长度定义为

为了提高预测的有效性，减少系统计算负荷，划定一定范围的监视区域，过滤掉一些遥远车辆的换道信息或邻近车道车辆摇摆的非换道行为信息，只有当旁车真实发生换道进入监视区域的行为才需要进行预测。

为了确定监视区域的合适范围以及进行后续的神经网络模型训练，从实际道路环境下采集了大量的直行道路切入换道过程参数。具体采集过程如下：用于换道的车辆加装了雷达、Mobileye摄像头和NAV982 GNSS惯性导航仪，换道车辆主动并线驶入另一车道正常行驶的两车的间隙中，通过雷达和Mobileye摄像头记录前车位置与速度参数，通过惯导记录下换道车辆的行车轨迹与运动参数，由于事先对道路坐标信息进行标定，因此可以利用坐标变换，将换道车辆的地理信息位置换算为车辆坐标系下与目标车道前车的相对位移参数（Δx，Δy），尺寸参数如图1所示。

在实际驾驶环境中，主车通过以下两种途径获取车辆运行状态信息：一是基于自身雷达和摄像头直接获取视野内车辆的速度与距离信息，距离信息比较准确，但是运动参数误差较大，由于Mobileye摄像头图像处理过程耗时较长，设备数据更新周期接近10 Hz；另一方面，基于惯导周期性的获取车辆状态以及驾驶员的操作参数，可准确获取航向、速度和转向盘角度等信息，采样频率可调，设定惯导采样频率为10 Hz，因此可认为两组传感器获得的数据为同一时刻的车辆实时状态信息。车道变换操作由4个独立阶段组成：意图阶段、准备阶段、过渡阶段和完成阶段［14］。为了提高数据训练样本的有效性，对训练样本数据有效区间进行剪切，截取数据持续时间必须大于10 s，确保训练样本数据中既有横向换道数据，又包含直线行驶数据；为了减轻数据噪声的影响，根据信号的不同性质，对数据的变化进行滤波以平滑时间序列差异，并过滤掉微小参数降低噪声的影响。

分析采集到的换道数据可知：转向盘转角和航向角变化趋势相同；换道过程中横向加速度大多数相对较小，部分时刻的采集数据与惯导的零漂数据发生混淆，不利于与并线行为建立相关性；车道变换期间，换道车辆与前车的纵向距离跟换道车速之间没有绝对相关性，因为任何车速下驾驶员都可能选择进行平稳换道、加速换道或者减速换道，本文中暂时不区分3种换道之间的细微差别。另外，惯导采集自身的三轴速度、加速度等，三轴方向正置于车辆中间位置，但是车辆平稳换道过程横向移动速度普遍较低，因此采集的高速航向车速较为准确，而垂直于航向的横向车速不精确。由于主要关注于车辆的横向轨迹，最终选取了换道车辆的航向速度v、转向盘角度α、航向角φ以及与目标车道前车的相对距离Δx和Δy对换道行为进行描述，并令ζ＝［v，α，φ，Δx，Δy］T∈R5×1。

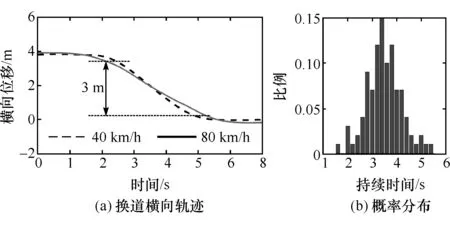
图2 换道横向轨迹与换道持续时间概率分布图

在整个车道变换过程的跨线中间阶段，横向移动速度变化范围不大，图2（a）描绘了两种车速下的横向换道轨迹，从图中可以看出，换道过程横向移动过程的中间段位移可近视为直线，可认为横向阶段性的匀速移动。文献［15］中基于美国NGSIM数据研究，统计得到车道变换时间满足正态分布，超过99.7%的车辆在12 s内完成车道变换，其统计方法的起点与终点边界范围较大，且多数为自由无压力换道过程，不适用于本文中的统计过程。图2（b）统计了本文中采集切入数据中横向位移跨度3 m内的换道持续时间，超过90%的持续时间大于2.8 s，即换道中间阶段，大多数车辆横向移动速度小于1 m／s。我国高速公路上的四车道、六车道和八车道的标准车道宽度分别为2×7.5 m、2×11.25 m和2×15 m，即单车道宽为3.75 m，由于大多数小汽车的宽度在1.8 m左右，这意味着在单车道内，单车道内车辆两侧各有接近0.9 m的活动区域。当发生换道行为时，按照平均1 m／s的横向移动速度，换道车辆的车头外沿在越过本车道线后，需要0.9 s的时间驶出邻车道的活动区域切入碰撞区域，为了确保能够完全监控接近1 s的切入过程，划定监视区域的Lw2为1 m。

2 预测模型设计

人工神经网络（artificial neural networks，ANN）是描述和预测非线性系统最有效的工具，本文中采用NAR神经网络搭建循环预测网络，进行驾驶员换道行为建模。使用历史参数训练NAR神经网络模型，并基于当前可用状态值预测不同系统输入的未来模式，即利用转向盘角度、航向速度、航向角和车辆相对位移参数作为模型的外源输入，对车辆的横向轨迹进行建模。设定神经网络有1个隐藏层、20个节点和20步短期记忆，这意味着网络使用2 s的过去信息进行预测下一步状态参数。由于神经网络训练过程是自由随机的，节点的数量设置并非固定，在训练过程中按照75∶15∶10的划分依据将数据分为训练集、验证集和测试集，在多次训练结果中，以较小的均方差作为评判指标选取合适的网络模型参数。

在应用NAR网络预测时，设定预测步数q为10步，基于历史驾驶数据ζ1：t-1和当前时刻的观测数据ζt预测下一步状态ζt＋1，并通过迭代算法预测车辆未来tp时刻的状态ζt＋1：t＋tp，根据每步的预测结果计算对应的未来横向移动距离，具体算法如表2所示。

表2 估计预测计算过程

上述Ls2为车辆横向宽度的一半，设定Δt与数据采样频率一致，Δt＝0.1 s。在系统时间进入到下一次计算周期时，用最新的观测数据覆盖旧的观测数据，循环采用算法1预测新观测数据下的未来10步值。为了检验所训练网络的预测效果，使用一组全新的换道和直行原始数据进行预测，如图3所示，图3（a）为换道行为，图3（b）为非换道行为。从图中可以看出，针对真实的换道行为或者横向晃动的非换道行为，虽然NAR迭代预测网络的计算结果与真实值之间存在一定的误差，但预测值与真实值变化趋势相同，误差在可接受的范围内，有理由认为所训练的网络可用于换道行为的预测。

图3 NAR网络预测的横向行为轨迹

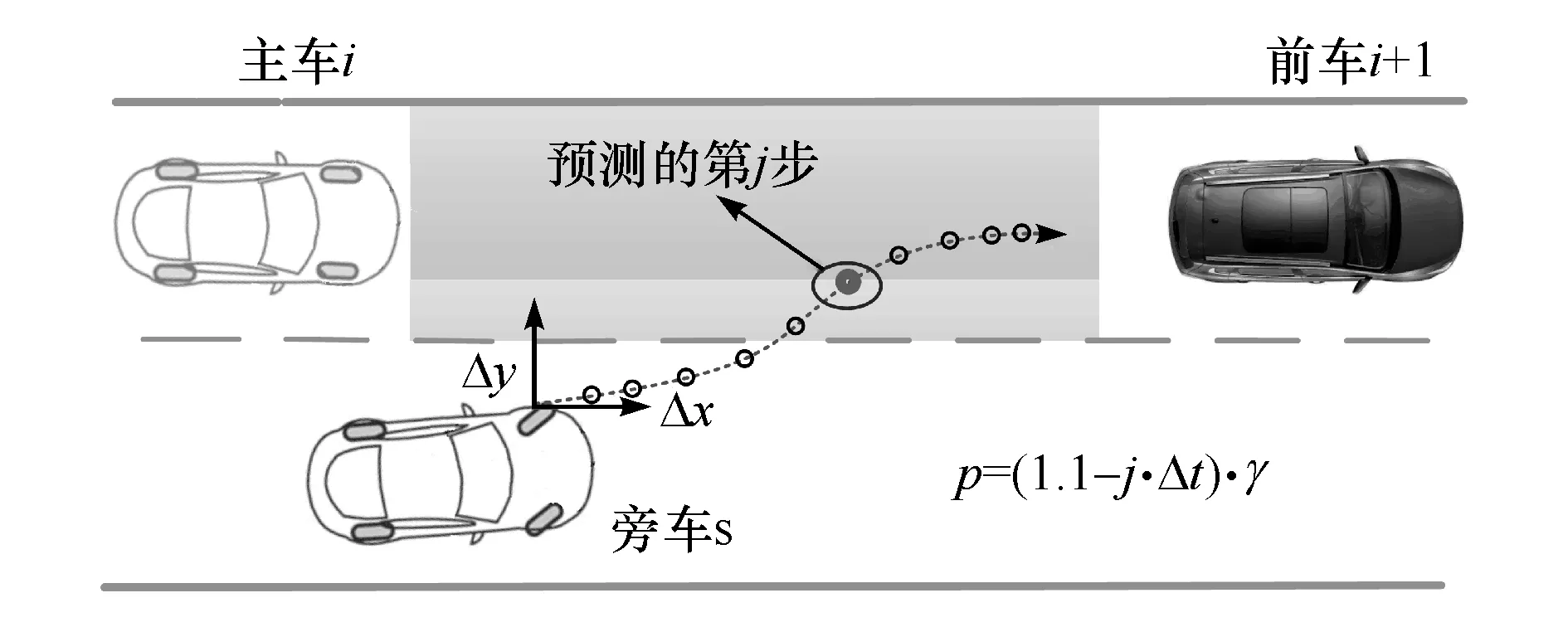
图4 预测步与切入概率示意图

3 切入概率计算与跟车策略

根据横向移动距离Δy＾t＋（j＋1）Δt和监控区域的宽度Lw2构建车辆的切入概率p计算模块，将预测结果转化为0到1之间的概率值。首先根据算法1预测当前时刻下未来旁车与前车间横向距离，同时循环计算第j步时旁车的横向移动距离，并判断此移动距离下旁车是否进入碰撞区域。若预测步中没有任何计算值超过Lw2，取p＝0；当预测步中有车辆进入碰撞区域时，设第j步为预测步中车辆第一次进入碰撞区域，见图4，则取p＝1.1-j·Δt，i＝1，2，…，10；若j步之后出现不连续的预测步越过监控区域时，统计第j步及之后预测进入碰撞区域的次数为n，在切入概率计算中引入置信因子γ＝n／（11-j），则当前时刻下，旁车切入概率p计算公式为

现使用一组全新的换道数据，通过预测网络及切入概率计算方法获得实时的预测切入概率，如图5所示，图中实线为采集的车辆真实横向位移数据，选定其中横向跨度1 m的数据作为监控区域的对比数据，使用前2.6 s的状态数据作为初始测量值，利用迭代NAR网络预测未来横向1 m跨度内的每100 ms的最大切入概率，绘制为图中虚线。从图中可以看出，预测的切入概率值非连续变化，且变化率与真实横向位移有一定的差异，但总体上预测的切入概率值逐渐增大到1，与车辆驶入监控区域的真实情况相符合。

图5 换道轨迹及其切入概率预测示意图

在传统CACC系统中，根据式（1）计算实时的跟车距离误差：

式中：Li为主车的长度；xi和xi＋1分别为两车的纵向位置；drel，i为主车前保险杠与前车后保险杠之间的相对距离；δi为跟车距离误差。若两车的相对距离为雷达或摄像头直接测量所得，可忽略式（4）的计算过程。

在CACC稳定的队列跟车系统中，车辆之间保持相同的跟车距离，当邻车道车辆并入主车道后被突然识别为新的跟踪目标，主车往往会紧急制动来保证安全的跟车距离，易引发后续车辆的危险碰撞行为。因此，主车的跟车距离误差δi应该不仅考虑主车与前车之间的纵向距离，同时还需要考虑旁车的切入行为，进行动态调整期望跟车误差值。当旁车意图并入队列中的第i和i＋1车的间隙时，为了在达到新的平衡之前确保有足够的安全间隙保证旁车切入，提出了一个新的随机间距误差δi的定义：

式中μ为0到1以内的灵敏度系数，用于缓冲主车跟车距离误差变化的激烈程度。若无切入事件发生，令p＝0，主车与前车的距离误差式（6）与式（5）相同，通过调整主车车速实现与前车保持动态平衡；当p≠0时且逐渐增大时，μ越大，δi突变幅度越剧烈，下文中取μ＝0.5用于仿真计算；由于考虑切入概率的跟车距离策略式（6）能够提前获得间距误差，进而确保主车提前减速以减小跟车误差，拉大两车的纵向间隙。当旁车切入并接触到碰撞区域时，CACC系统需要将旁车更新作为新的跟踪目标车i＋1，而之前的前车编号变为i＋2，此后，巡航控制器控制系统按照新的目标进行跟车调整。

4 巡航控制仿真试验分析

联网巡航分层控制系统在设计控制算法时，采用之前的研究成果［16］，上层控制中引入了切入概率的计算，利用加速度前馈及误差反馈的控制算法计算实时期望加速度控制量；在底层控制中设计了加速度逆动力学模型查询表，直接根据期望加速度和当前的车速查询加速踏板和制动踏板开度，系统架构如图6所示，其中控制器算法如图6中虚线框所示。

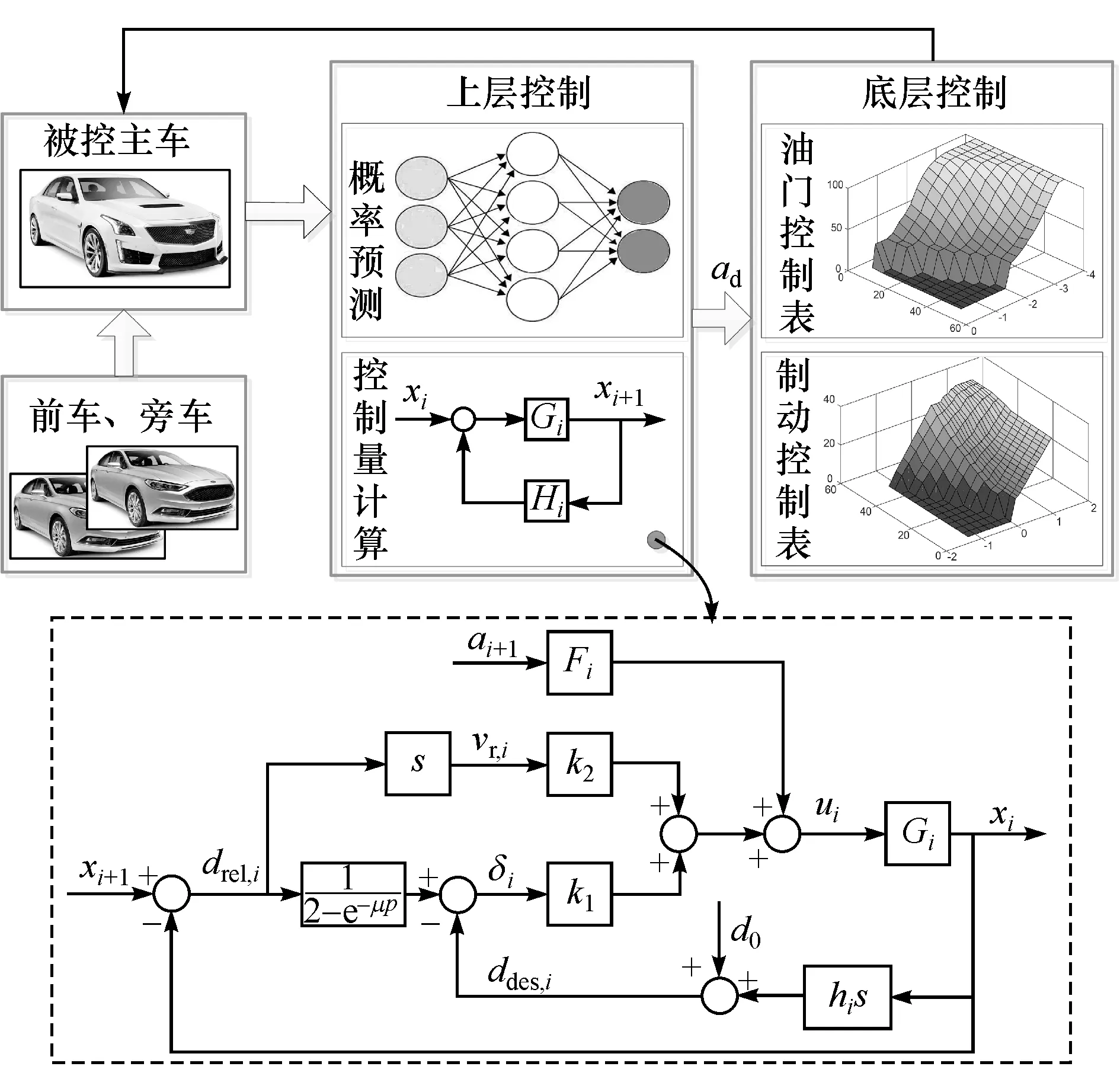
图6 基于预测的联网巡航控制系统架构图

文献［16］中详细论证了所设计控制器算法的稳定性，可以实现快速准确的控制响应，本文中着重分析所设计的切入概率模块对主车跟车响应的影响。参考上述控制器，设定k1＝0.3，k2＝0.5，k3＝0.6，其中k3为Fi的近似值，驱动响应的1阶惯性延迟环节中，Gi取惯性时间为0.1 s，时间延时为0.3 s，仿真试验中忽略V2V通信延迟，因为未来基于5G的通信延迟将会更低。

参照图4所示场景，在Matlab／Simulink中建立3车的两种跟车并线试验，一种是针对式（5）动态跟车策略的NAR-CACC跟车仿真，一种是不考虑旁车并线过程式（4）的CACC跟车仿真。两种仿真中，所有车辆均以25 m／s的速度匀速行驶，设定车间时距h＝1.2，停车距离d0，i为3 m。旁车初始纵向距离前车10 m，与主车保持等速行驶，待主车与前车达到稳态平衡后，旁车逐渐移动到主车与前车的间隙中。旁车的仿真行为参数采用之前采集到的实车数据进行数值模拟。图7显示了针对两种不同跟车距离控制策略下主车的响应效果，其中图7（a）为主车与前车的速度误差曲线，图7（c）为跟车距离的误差曲线，图7（b）和图7（d）分别为主车的加速度及速度曲线。

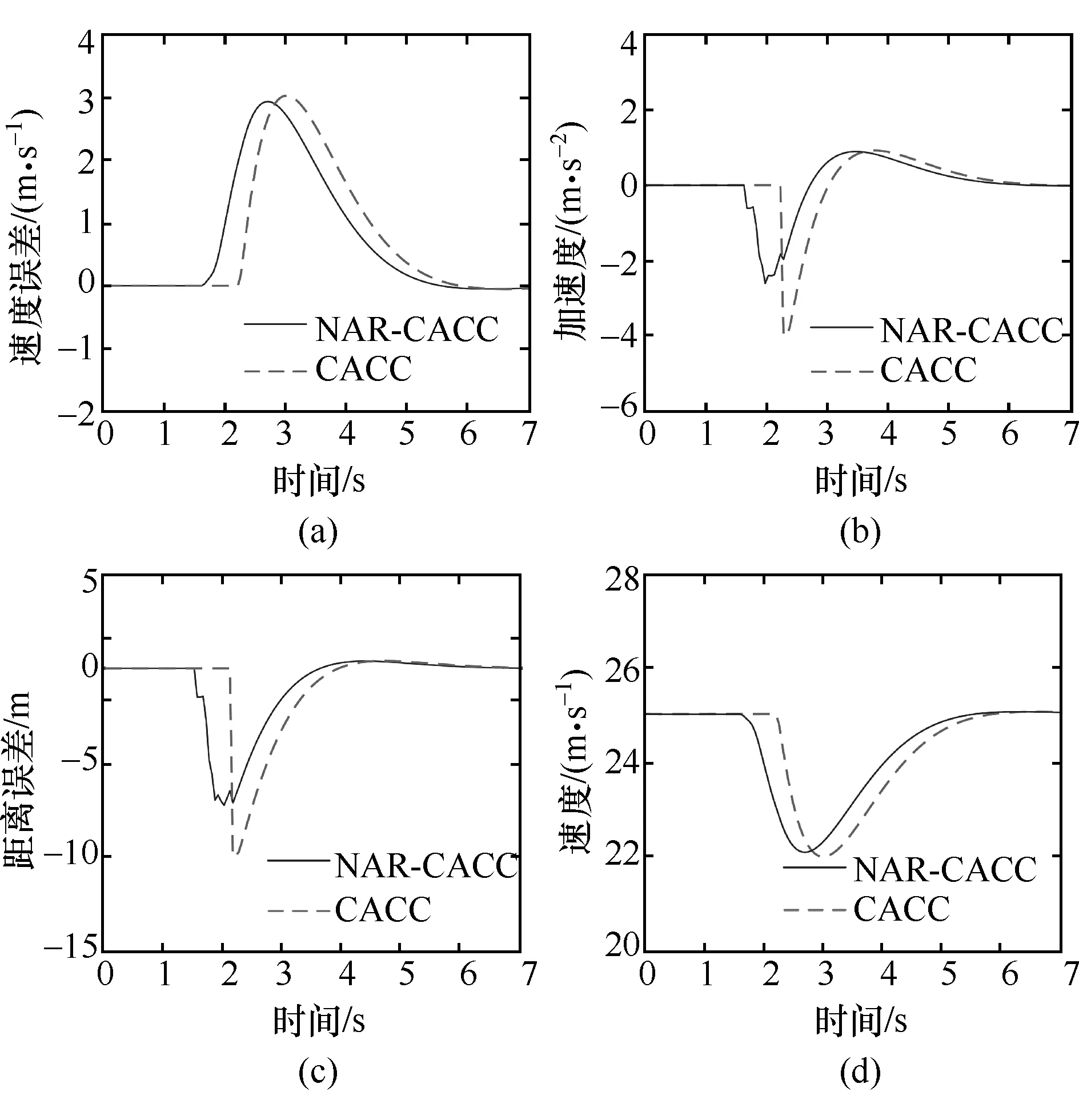
图7 网联跟车仿真主车响应曲线

从图7（a）和图7（c）中可以看到，在两种跟车策略下，主车与前车的纵向距离和速度误差均趋于0，即主车均能够达到最终的稳定平衡。值得注意的是，NAR-CACC跟车策略相比较传统CACC跟车策略，系统可以更早地开始响应旁车的切入行为。观察图7（b）的加速度曲线可知，在旁车切入时，由于NAR-CACC策略下主车提前进行缓慢制动而不是紧急制动，而传统CACC策略下剧烈突变的加速度影响乘坐舒适性，同时紧急制动行为会严重影响交通安全性与交通流通性。观察所有NAR-CACC策略下曲线变化，主车在各方面响应表现都更加优异。提前响应的时间值取决于NAR网络的预测结果，由于NAR网络预测采用迭代预测，而预测的时间步越多，其预测结果误差越大，因此本文中并未使用更远的预测步结果来增加预测时间，而是结合监控区域的尺寸以及固定的预测步数限制，进行旁车并线切入概率计算。综上可知，考虑旁车并线预测的NARCACC跟车策略可使主车的跟车响应更早、更快、更安全，有利于提升车队的交通安全性。

在相同的仿真条件下，取不同的μ值，观察主车的速度与加速度响应变化特征，如图8所示，灵敏度系数μ取值越大，主车的速度与加速度变化幅度越大，且能更早地达到速度平衡；从图8（b）的加速度曲线可以看出，μ取值越大导致加速度变化较大，降低了驾驶的舒适性，因此需要根据不同跟车速度与跟车距离选择合适的μ值。未来可以继续探讨不同切入行为下，跟车误差距离变化程度对车辆响应行为的影响特点，在确保安全性的同时，提升驾驶的舒适性。

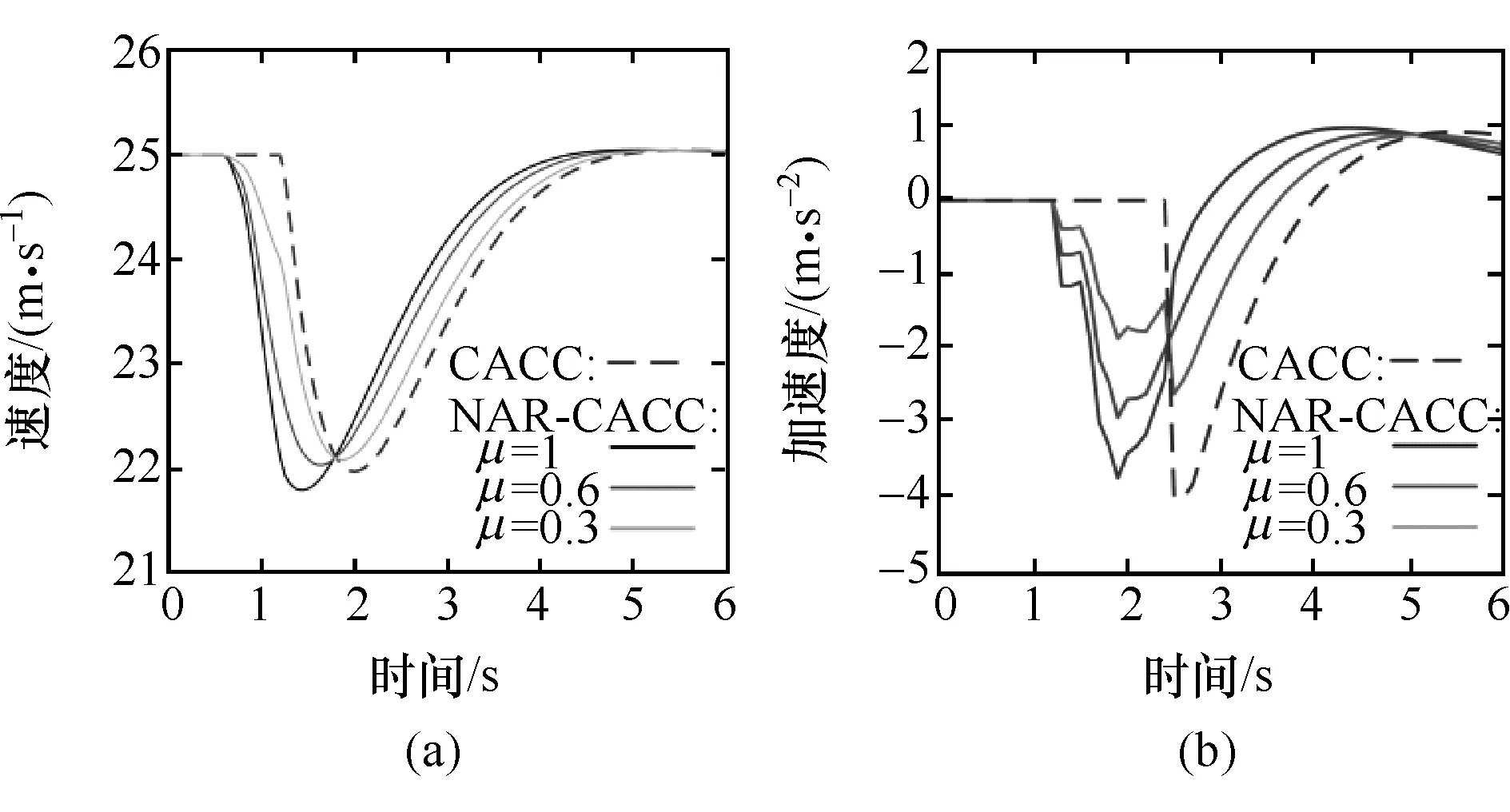
图8 不同灵敏度系数下的主车速度和加速度变化曲线

5 结论

本文中以网联电动车辆为基础，依靠采集的实车并线行为数据对NAR神经网络进行训练，通过预测模型迭代循环计算旁车的切入概率，并设计了一种考虑切入概率的跟车误差策略，最后使用真实并线数据进行Matlab仿真试验跟车。结果表明所设计的并线切入预测算法可以有效检测旁车的并线切入行为，添加了切入概率预测模块的网联CACC系统可以更早、更快地响应旁车并线时的跟车目标变化，提升乘坐的舒适性，保障了车队行驶的安全性。

由于受试验条件限制，本文中未能开展真实路况下多车实时通信的并线行为在线预测与巡航控制试验，同时由于训练样本多为中低速直线工况数据，算法在弯道下的效果还有待分析，测试结果针对不同驾驶员行为预测的泛化能力还有待研究。