表面形貌测量系统中光纤传感器的数据融合算法

杨瑞峰，杨 睿，郭晨霞，吴 耀

(1. 中北大学 仪器与电子学院，山西 太原 030051；2. 山西省自动化检测装备与系统工程技术研究中心，山西 太原 030051)

0 引 言

随着精密和超精密制造业的发展，对高精度、 高分辨率的表面形貌测量技术的需求日益显著[1]. 表面形貌在很大程度上影响着精密器件的技术性能和使用功能，例如精密齿轮表面、 高集成度的电子电路表面、 精密光学器件的表面等. 将光纤传感技术用于表面形貌的测量可实现非接触式、 抗电磁干扰能力强、 稳定性好的优点[2-4]. 光纤传感器测量表面形貌系统中的光电转换器是用以实现光信号和电信号的转换，但其中固有的热噪声和散粒噪声等会影响测量系统的测量精度，且热噪声和散粒噪声都属于高斯噪声. 在测控系统中，对于噪声的主要抑制方法为采用相关的硬件电路来滤除、 隔离和屏蔽[5]. 除了这些方法外，减小高斯噪声的影响常常采用数理统计的方法[6].

表面形貌测量系统采用单一的光纤传感器进行数据采集，单个的光纤传感器在不同情况下测量的数据会有差异，对某个固定位置测量时，利用多个测量值进行数据处理来提高数据的可信度十分必要. 蔡菲娜等[7]将单传感器的测量值进行分组，利用极大似然函数估计导出数据融合公式对多次测量值进行数据融合，证明了单传感器系统中，分组融合的估计效果优于单组算术平均的估计效果，这种方法对分组依赖程度高，分组不恰当会影响融合结果. 李军等[8]证明了对单传感器来说统计加权融合的数据融合方法优于基于关系矩阵的数据融合方法，从概率统计学的方面对有效值进行了加权融合. 卡尔曼滤波在数据融合方面具有广泛的应用[9-10], 通常是以最小均方误差为准则的递推无偏估计算法，利用前一时刻的系统状态估计值和当前时刻的系统状态观测值，并根据系统的过程噪声和观测噪声来更新系统状态变量的估计值，使系统当前的状态估计值能够充分逼近真实值.

针对以上问题，本文提出了基于关系矩阵的统计加权融合算法，并将其与基于卡尔曼滤波的均值融合算法同时应用于表面形貌测量数据的处理，最后对这两种算法进行了对比分析评价.

1 光纤传感器表面形貌测量系统

表面形貌测量系统由光纤传感器、 半激光器、 高精度电动位移台、 光电探测器和上位机组成. 测量系统实物图如图 1 所示.

利用光纤传感器测量表面形貌的原理是： 半导体激光器作为光源与光纤传感器中的单模光纤(发送光纤)耦合，光进入光纤传感器，再经由光纤传感器将光发送到被测件表面，经被测件表面的反射光再由光纤传感器中的接收光纤捕获，结合光纤传感器的结构和出射、 反射光强构建调制特性函数. 调制特性函数可以反映出距离和光强之间的线性关系，光电探测器接受到光强之后经过解调可以得到该位置的位移信息. 扫描整个被测件表面，利用Matlab进行数据预处理和显示就可以得到被测件的表面形貌.

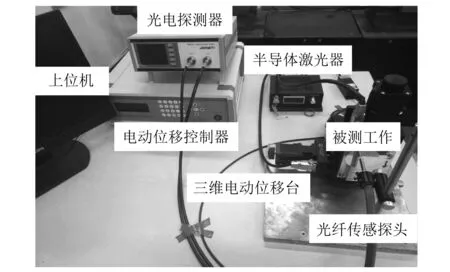
图 1 光纤传感器表面形貌测量系统Fig.1 Optical fiber sensors in surface morphology measurement system

2 基于关系矩阵的统计加权数据融合算法

基于关系矩阵的数据融合算法是利用关系矩阵得出测量值之间的互相支持程度，确定有效测量值，剔除无效测量值[11]，然后根据极大似然法估计有效测量值的融合数据. 但其中阈值的选取带有很大的主观因素，且对有效测量值进行融合时只是简单地取平均值. 不同的有效测量值和真实值之间偏离程度是不同的，给不同的有效值赋予不同的权重，能够更为客观地对有效测量值进行数据融合. 因此在基于关系矩阵的数据融合算法的基础上，引入传感器测量值的统计规律，依据“3σ法则”去除无效测量值，根据有效测量值的概率分布，确定置信概率向量，归一化后可以得到有效测量值的加权向量，最后利用加权向量和对应有效测量值的乘积作为最佳融合数据.

算法的基本步骤如下：

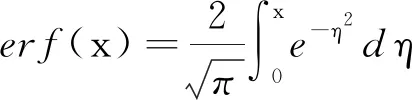
2) 选定一个阈值ξ和置信距离测度作比较，当置信距离测度小于阈值时就认为两个测量值互相支持，否则就不支持. 支持用1表示，不支持用0表示. 利用此方法可以得到关系矩阵R，其中rij表示xj对xi的支持程度，

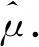
设

i=1,…,m,

(1)

则似然函数为

(2)

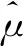
3) 根据“3σ法则”去除无效测量值，(当X=(x1,x2,…,xn)服从高斯分布时，测量值落在[μ-3σ,μ+3σ]区间内的概率为99.774%，认为落在该区间内的测量值都是有效的)，根据有效测量值的概率分布，确定置信概率向量，以一个σ的大小作为划分单位可以得出置信概率向量如表 1 所示.

表 1 置信概率向量Tab.1 Confidence probability vector

3 基于卡尔曼滤波的数据融合算法

光纤传感器测量表面形貌系统的输入量为光强，输出量为位移，由表面上多点的位移构造表面形貌，所以该测量系统是线性的. 而且其每个时刻的测量值都是独立的，符合贝叶斯滤波的马尔可夫假设. 因此可以采用卡尔曼滤波技术来滤除系统中光电探测器的高斯噪声，然后完成数据层的数据融合，以提高表面形貌的还原精度. 卡尔曼滤波算法的主要过程如下:

光纤传感器测量表面形貌系统是一个线性系统，所以该系统的状态方程和观测方程可以用下式表示

x(k)=A·x(k-1)+B·u(k)+w(k),

(3)

z(k)=H·x(k)+y(k),

(4)

式中：x(k)为k时刻系统的状态；z(k)为系统的观测值；u(k)为控制量；w(k)和y(k)为符合高斯分布的测量噪声，其协方差分别为Q和R;A、B、H为系统参数.

卡尔曼滤波实际上是一个迭代的过程，每得到一个新的观测值迭代一次，每迭代一次都要更新系统状态和协方差，每一次迭代都分为两个步骤：迭代和修正. 预测是根据前一时刻迭代的结果，即利用x(k-1|k-1)和P(k-1|k-1)来预测这一时刻的系统状态和误差协方差，得到x(k|k-1)和P(k|k-1)为

x(k|k-1)=A·x(k-1|k-1)+B·u(k),

(5)

P(k|k-1)=A·P(k-1|k-1)·AT+Q.

(6)

计算卡尔曼增益K(k)，结合这一次的实际测量结果用于修正系统状态x(k|k)和P(k|k)，得到最新的x(k|k)和P(k|k). 至此可以得到想要的滤波后的值x(k|k). 因为在光纤传感器测量表面形貌的系统中，测量值是位移，此时没有控制量的参与，于是B·u(k)=0，另外将参数A、H也取为1，则整个滤波过程可以用以下3个式子来迭代

K(k)=P(k|k-1)/P(k|k-1)+R),

(7)

x(k|k)=x(k-1|k-1)+K(k)·

(z(k)-x(k-1|k-1)),

(8)

P(k+1|k)=(1-K(k))·P(k|k-1)+Q.

(9)

x和P(P不为0)的值可以任意取，卡尔曼滤波器可以自适应不合理的取值，在光纤传感器测量表面的系统测量精度大约在20 μm左右，所以Q取1e-10，R取4e-10，x取0，P取1. 因为表面形貌测量系统中的传感器是单传感器，所以无法对其使用传感器加权融合，因此对滤波后的数据进行均值融合.

4 两种数据融合算法的比较

为获取同一测量点的多次测量值，用光纤传感器反复扫描同一段直线. 如图 2 所示，实验中光纤传感器距离被测表面0.05 mm进行扫描，扫描步长为0.2 mm，扫描总长度为2 mm，来回扫描10次，同一测量点会得到20个测量值. 以第4个测量点(沿测量直线，距离原始测量点 0.2 mm 处)的位移数据为例进行基于关系矩阵的统计加权数据融合算法和基于卡尔曼滤波的均值数据融合算法进行数据融合. 实验中直接测量到的是光强数据，根据光强和位移的调制特性曲线p=1.376d+0.243可以得出对应点的位移，其中p为接收光纤中接收到的光强值，单位为mW；d为光纤传感器和被测面的距离，单位为mm. 20个测量点的数据如表 2 所示.

图 2 数据融合测量点的扫描方式Fig.2 Scanning method of data fusion measurement points

表 2第4个测量点往返10次得到的20个测量值

Tab.220 Measurements obtained by roundtrip 10 times from 4th measurement point

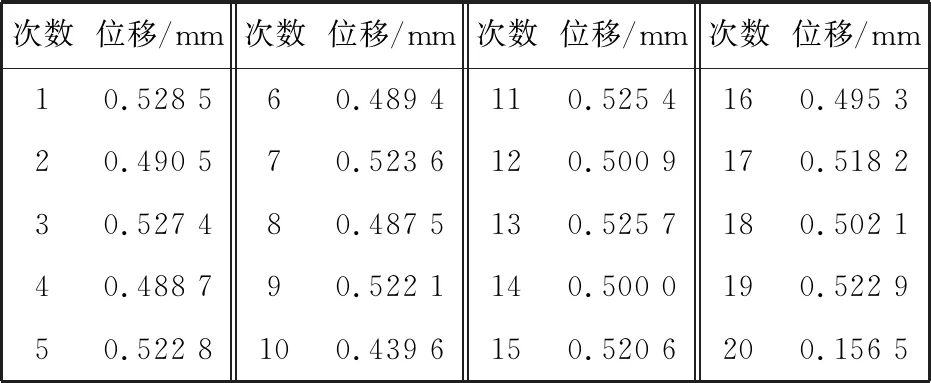
次数位移/mm次数位移/mm次数位移/mm次数位移/mm10.528 560.489 4110.525 4160.495 320.490 570.523 6120.500 9170.518 230.527 480.487 5130.525 7180.502 140.488 790.522 1140.500 0190.522 950.522 8100.439 6150.520 6200.156 5

4.1 基于关系矩阵的数据融合算法实例

首先，结合光纤传感器对同一测量点测得的数据，借助误差函数得到置信距离矩阵，选择阈值为ξ=0.9, 第4个测量数据的关系矩阵为

由关系矩阵可以直观地看出，第1、 2、 19、 20次的测量数据点不被其他数据所支持，所以这4个点被认为无效测量值. 剔除无效测量值之后，得到有效测量值的集合为

D=[0.542 7 0.488 7 0.522 8 0.489 4 0.523 6 0.487 5 0.522 1 0.493 6 0.525 4 0.525 7 0.500 0 0.520 6 0.495 3 0.512 8 0.502 1 0.522 9].

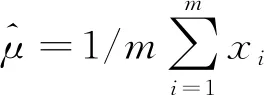
两次迭代后对应的置信概率向量和加权向量分别为

P=(0 0 0.135 9 0.135 9 0.341 4 0.135 9 0.341 4 0.135 9 0.341 4 0.135 9 0.341 4 0.341 4 0.341 4 0.341 4 0.135 9 0.341 4 0.341 4 0.341 4 0 0),

W=(0 0 0.030 6 0.030 6 0.077 0 0.030 6

0.077 0 0.030 6 0.077 0 0.030 6 0.077 0 0.077 0 0.077 0 0.077 0 0.077 0 0.077 0 0.077 0 0.077 0 0 0).

重复以上步骤，可以得到测量直线上50个测量点对应的最佳融合数据，融合后的数据如表 3 所示. 将融合数据和3组原始数据(第2次去向数据、 第3次回向数据、 第7次去向数据)做比较以观测融合数据融合效果，对比图如图 3 所示. 由图3可以看出，基于关系矩阵的统计加权数据融合算法有较好的融合效果.

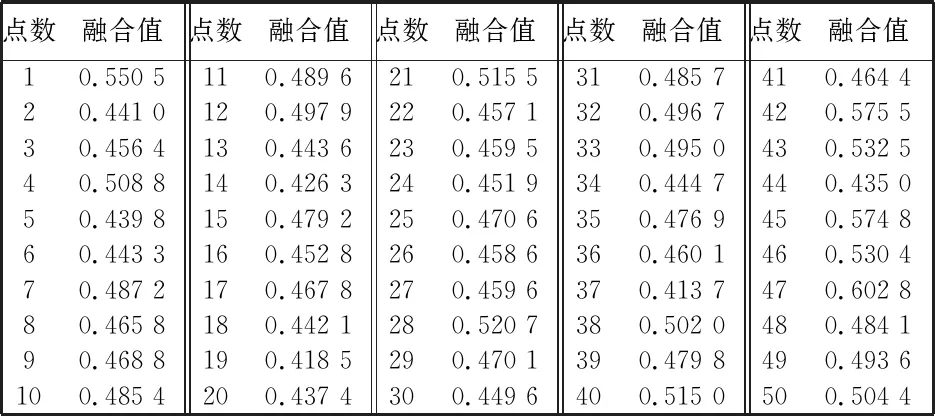
表 3 数据融合后的测量直线上50个点的融合值Tab.3 Fusion value of 50 points on measured line after data funsion

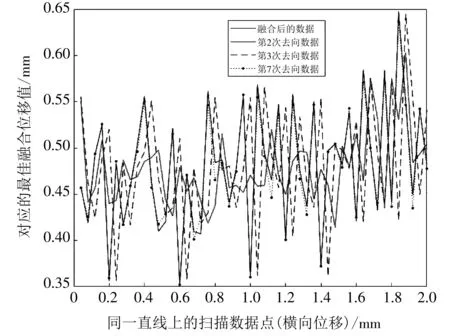
图 3 融合数据与原始数据对比图Fig.3 Comparison between fused data and original data

4.2 基于卡尔曼滤波的数据融合算法实例

光纤传感器测量形貌系统中存在多种噪声，对测量的数据进行卡尔曼滤波可以有效地去除数据中光电探测器中的热噪声和散粒噪声等高斯噪声给测量带来的影响，以跟踪被测形貌的参数的真实值. 在此选取扫描直线上的50个数据点进行卡尔曼滤波，然后对20次测量值经卡尔曼滤波后的结果进行均值融合，结果如表 4 所示. 下面以第5次测量值作为滤波对比实例，图 3 为滤波前后的对比图.

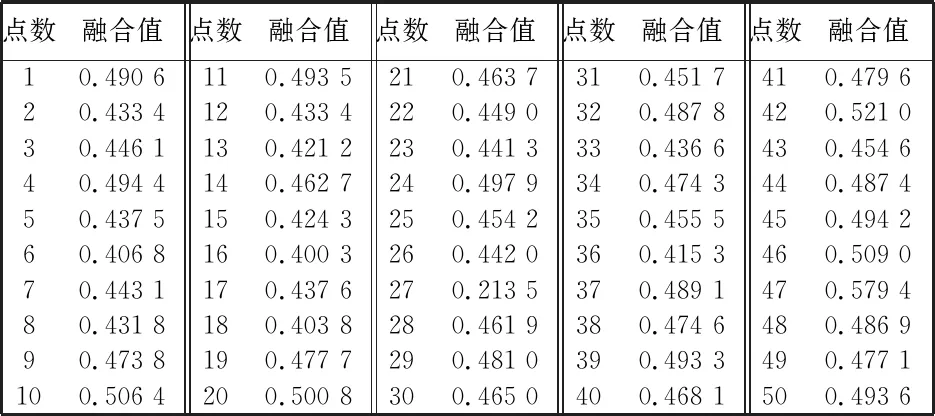
表 4 数据融合后的测量直线上50个点的融合值Tab.4 Fusion value of 50 points on measuring line after data fusion

图 4 卡尔曼滤波后的数据对比图Fig.4 Data comparison chart after Kalman filter

4.3 两种数据融合算法融合结果对比分析

对20次的测量值进行卡尔曼滤波后再进行均值融合，将基于卡尔曼滤波的均值融合后的数据和基于关系矩阵的统计加权融合后的数据进行对比分析，如图 5 所示.

图 5 两种数据融合算法融合结果对比Fig.5 Comparison of fusion results between two data funion algorithms

基于关系矩阵的统计加权数据融合算法是基于关系矩阵的融合数据进行的加权融合，而初步的融合数据是根据最大似然法给出的估计值，因此可以将均值和标准差看作是测量值的有效估计. 这两种数据融合算法也可以看作是两种数据处理工具对相同的测量值进行数据处理，因此，也可以采用变异系数来表示融合后的数据和原始测量值的偏离程度.

因为均值相差较小，所以对比两种融合数据的标准差的大小来判断两组数据和真实测量值的偏离程度，如表 5 所示. 由标准差和变异系数的对比可知，经过基于卡尔曼滤波的数据融合算法处理的数据具有更小的标准差和变异系数.

表 5 两种融合数据的对比Tab.5 Comparison of two fused data

5 结 论

针对光纤传感器测量表面形貌系统中的噪声会影响测量精度的问题，对光纤传感器对同一测量点的多次测量值进行了数据融合. 提出了基于关系矩阵的统计加权数据融合算法，通过理论分析及利用测量数据进行仿真实验对基于关系矩阵的统计加权数据融合算法和基于卡尔曼滤波的均值融合算法的融合效果进行了对比. 结果表明与基于关系矩阵的统计加权数据融合算法相比，卡尔曼滤波的均值融合算法具体更小的标准差和变异系数，能更精准地利用测量数据还原表面形貌.