基于贝叶斯推断的EM 算法对宁波地铁站点价值分级的研究

丁 悦，周健勇 （上海理工大学 管理学院，上海200093）

1 研究背景及目的

1.1 研究背景

近年来城市轨道交通处于一个持续发展的阶段，它给人们的出行带来了极大的便利。全国各地陆陆续续规划了大量的交通线路，而地铁线路的站点则是城市轨道交通线网中的一个关键节点，各地铁站点成为了城市社会经济活动中的热点区域，而又因为各种类型的站点在城市中的区域条件、交通功能、土地利用等存在一定的差异，所以对各个站点进行科学的分类，对城市功能的分区和评估城市轨道交通的建设有着重大意义。

本文对浙江省宁波市轨道交通的地铁站点进行抽样分级研究。宁波是中国大陆第21 个开通轨道交通的城市，截止到2019年7 月份，共有线路3 条，总长91 千米，第一条线路于2014 年5 月30 日开通运营，未来运营的路段将会接二连三开通。但是为了使地铁站点的利用价值更高，根据站点属性和周边情况，解决站点与客流不相匹配的问题，需要对站点的分级进行合理的优化，使得轨道交通的建设有更充分的意义。

纵观我国国内的站点分级现状，分级体系由来已久，也各有千秋。分级大体上可以总结为3 类，第一，以分时段客流量为指标；第二，以客流属性和周边环境服务为指标；第三，以它的地理位置和交通组织为指标。基于这些指标，国内研究者大多数是通过实地调研数据的方法进行分级，而随着数据挖掘的日趋成熟，可以通过更多的方式获取数据，使其更多的应用于城市空间中。而且国内对于站点分级的标准至今也未达成统一的共识，有的是将站点划分成4 个等级；有的是将站点划分成区域导向型；有的是划分成区域；有的是按照职能划分等。

从国外对于地铁站点分级的研究现状来看，他们大都是以城市站点为研究对象，郊区只作为其中的子类，一般是根据车站形式、客流量、服务区域等开放的空间场所特性为指标去给站点分级，比如韩国的首尔是从客流量去分析站点尺度；日本的东京将地铁站分为市区和郊区，再根据不同指标给站点进行分类等。在这些研究中，很多因素以及差异性受到了忽略，缺乏很多定量的标准。

1.2 研究目的

本文基于前辈研究的基础上，将浙江省宁波市地铁的64 个站点，根据站点基础、实际客流、周边情况等因素提取8 个主要指标，采用贝叶斯推断的EM 算法对主要指标进行聚类分析，并将站点科学地分为居住导向型、商业导向型、就业导向型3种类型，将每个站点赋予各个类型百分比。解决了之前单一的分级方法，这样可以获得更合理的结果，也能更好地对站点进行价值评级，促进城市轨道交通更好的发展；也为宁波市广告、通信、商业、TOD 的长远发展奠定了理论依据和参考价值。

2 算法介绍

2.1 EM 算法概述

EM 算法最早是Dempster、Laird 和Rubin 在1977 年提出的，通常是在数据不完备的静态数据模型中的期望最大化算法，简称EM 算法，是计算模型参数的最大似然估计值。EM 算法本质上是一种迭代算法，是根据上一步估计出的参数值来猜测隐变量最可能的值，再用猜测的值作为隐变量的值，重新估计参数的值，反复迭代计算，直至收敛，也就是似然函数值达到最大。每一次迭代都能保证似然函数值增加，并且收敛到一个极大值。它的每一次迭代包括两步：第一步求期望，称为E 步；第二步求极大值，称为M 步。EM 算法以及它的改进版本常常被用于机器学习算法的参数求解，包括高斯混合模型、概率主成分分析、隐马尔可夫模型等，用于解决数据缺失的问题。比如营销流程的管理、客流人群的筛选、图像分割、医学中的动物意外死亡、记录仪器发生故障、被调查者拒绝回答相关调查项目等。

2.2 符号的定义

本文对算法中的符号定义如表1 所示：

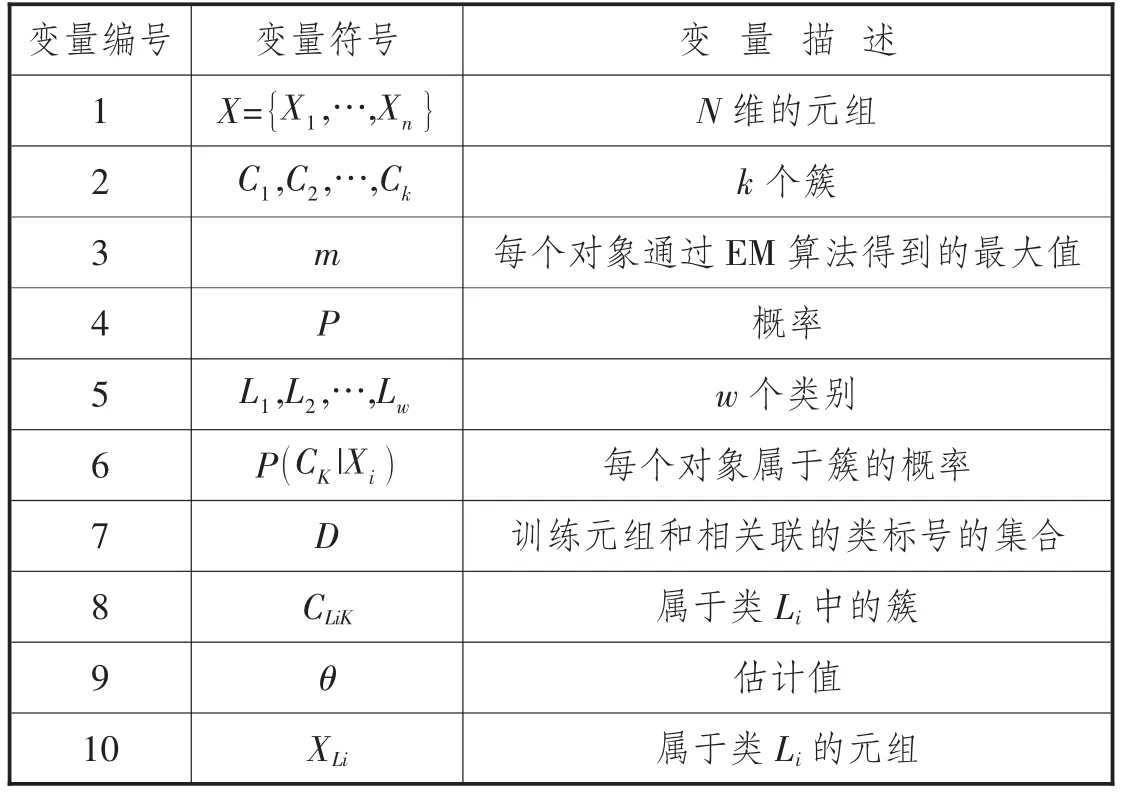
表1

2.3 构造似然函数

EM 算法给定相互独立的数据X=｛X1，…，Xn｝和含有隐变量Z和参数θ 的概率模型f（X，Z，θ ），根据极大似然估计理论，θ 的最优估计在似然取极大值时得出θ如果考虑表示缺失数据的隐变量，则：

以离散为例，用极大似然估计的方法对上式取自然对数：

引入隐分布q（Z），将对数似然：

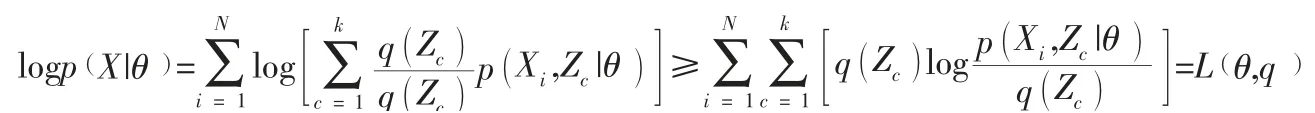
当右侧取全局极大值时，θ 至少使左侧取局部极大值，右侧表示为L（θ，q）后，则求解目标为其中L（θ，q）是似然优化估计的下限，EM 算法它的下限逼近对数似然的极大值。

2.4 传统的EM 算法

传统的EM 算法是一种迭代求精算法，它主要是由期望步和最大化步构成，最基本的思想是先估计出缺失数据的初值，再计算模型参数的值，然后再不断迭代E 步和M 步，不断更新，直至收敛。它的具体步骤如下：随机选择K个对象代表簇的中心，以此猜测其他数据；不断执行E 步和M 步直至收敛。

（1） E 步

（2） M 步

2.5 贝叶斯推断的EM 算法

在极大似然估计理论下，EM 算法随机选择对象作为簇的中心，只能给出参数θ 的单点估计，导致聚类的不稳定，以及边缘数据对算法影响过大，使得结果输出的正确率偏低。当引入贝叶斯推断的方法后，能够解决分布过度拟合的问题，首先对数据源进行分类，将分类结果作为使用范围，在每个类中反复执行E 步和M 步，直到收敛为止，充分利用EM 算法容易到达局部最优的点，使其更好的聚类，更快的收敛，得到更准确的数据填充值，在此基础上，引入P（θ|m），此时离散形式表示为：

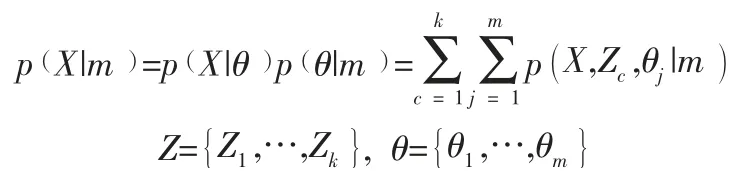
考虑隐分布q Z，（ ）

θ 后，可得隐变量的自由能：

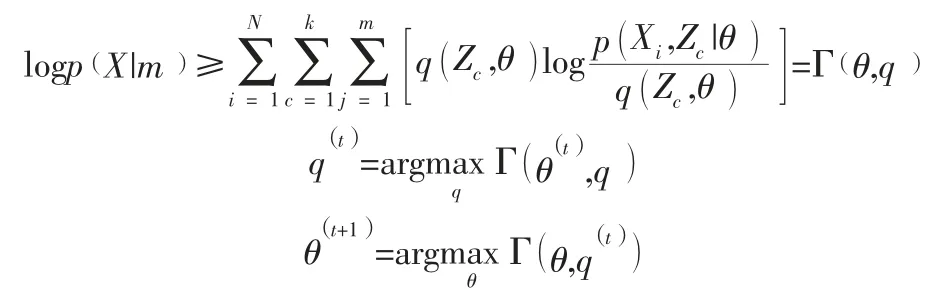
第二步：把结果作为新的数据集，在这些数据集中分别使用EM 算法计算期望最大值。E 步是用P（XLi∈CLiK）分别将Li中的XLi派到CLiK中。M 步是用之前得到的概率重新计算模型参数当算法收敛之后，用mLiK作为Li中k的最大化值，并用这个值填充缺失数字。

2.6 算法的实例

为了更好地说明此算法的应用，下面举一个二维指标的实例进行详细说明。首先构造1 000 个二维随机变量x1，x2，…，x1000，其中Xi=（ui，vi），i=1，2，…，1 000，且是由3 个高斯分布混合而成的。选取2 个指标分别于x轴、y轴，结果导向类型为3 种。

原始分布如图1（所有二维随机变量处于一个离散状态且有向3 个方向聚类的趋势）：

经过EM 算法运行后分布如图2 至图4 所示：

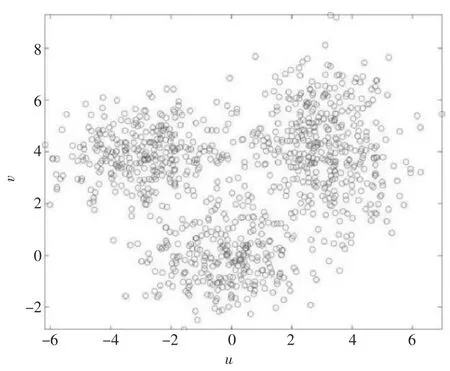
图1

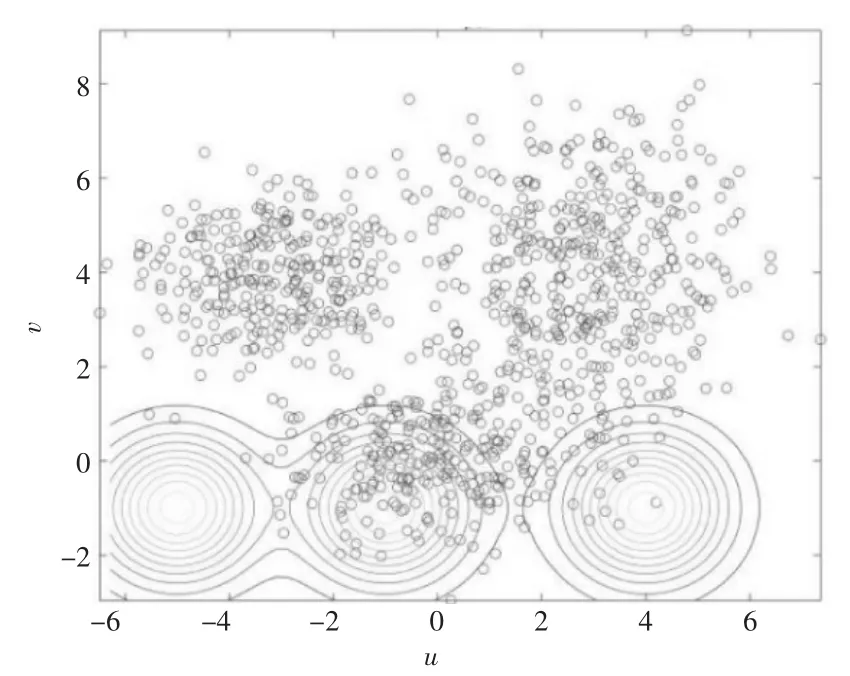
图2 初始图

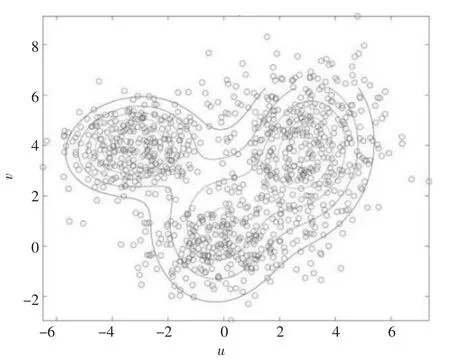
图3 中间图

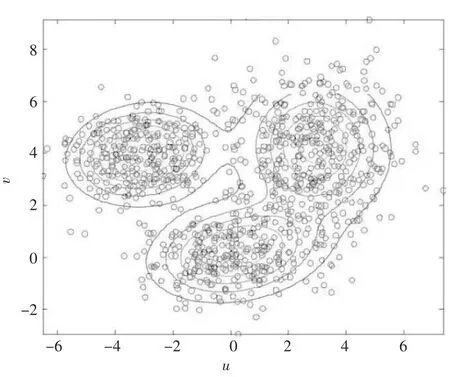
图4 结果图

经过EM 算法不断运行迭代，分布图逐渐会趋于一个收敛的状态，此时将其结果输出。在这个例子中，3 个样本的3 次结果导向类型的百分比数据见表2，可见这3 个样本逐渐走向同一个趋势，因为各自结果百分比也是逐渐收敛，此时将每个样本的结果数据输出，得到各个类型百分比。然后根据的百分比结果，结合具体应用再分析。

表2 其中3 个同类别样本输出的数据

3 实验过程及结果分析

3.1 主要指标数据

基于宁波轨道交通地铁站点的现状，本文对宁波地铁64 个站点进行深入的分级研究。综合轨道交通站点的现状和一些文献研究的基础上，本文从站点基础、实际客流、周边情况等方面提取了8 个主要指标进行评级研究，分别是早高峰真实客流进出比、客流偏度、客流高峰小时系数、客流时段分布均衡系数、周边居民区数量、周边公交数量、周边商场人流量、周边写字楼数量。表3 为其中12 个站点的指标数据。

表3 某中一些站点的指标数据

客流偏度是数据分布形态的量，表示总体取值分布的对称性，其需与正态分布作比较，当客流偏度为0 时，数据分布形态和正态分布的偏斜程度相同；当客流偏度大于0 时，右偏；当客流偏度小于0 时，左偏。

客流高峰小时系统数P的定义为：P=Qi/Qd。其中，Qi表示第i小时的客流量；Qd表示全天的客流量；P的最大值即为客流高峰小时系数。

客流时段分布均衡系数U的定义为：U=G/H。其中，G表示高峰时间段的小时平均客运量；H表示平峰时间段的小时平均客运量；当U＞2 时，表示很不均衡；当1.6≤U≤2 时，不均衡；当U＜1.6 时，较均衡。

3.2 数据预处理

数据预处理就是对数据进行规范化的处理，以便于接下来进行数据挖掘的工作。当从不同维度去评价指标时，往往呈现的结果在数据值上的差异性非常大，如果没有数据预处理的过程，则会对后续的数据分析有一定的影响。一般的预处理就是将数据按照一定的比例放缩，使其维持在一个特定的数值区间内。在某些指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

z-score标准化：

标准分数也叫z分数，它是一个分数与平均数的差再除以标准差的过程。用公式表示为：z= x-（ ）

μ /σ。其中：x为某一具体分数，μ 为平均数，σ 为标准差。z值的量代表着原始分数和母体平均值之间的距离，是以标准差为单位计算。在原始分数低于平均值时z为负数，反之则为正数。

标准差计算公式：

假设有一组数值X1，X2，X3，…，Xn（实数），其平均值为μ，标准差公式为：它是一组数据平均值分散程度的度量，一个大的标准差，代表大部分数值和平均值间差异大；一个小的标准差，代表这些数值较接近平均值。

表4 为其中12 个站点的指标数据预处理结果。

表4 数据预处理的结果

3.3 聚类过程

聚类分析是应用最广泛的一种分类技术，它把性质相近的个体归为一类，使得同一类中的个体具有高度的同质性，不同类之间的个体具有高度的异质性。聚类分析的职能是建立一种分类方法，它是将一批样品或变量，按照它们在性质上的相似程度进行分类。

本文采用贝叶斯推断的EM 算法对站点进行评级分析，将8 个指标聚合成两类，分别为客流情况和周边情况，去除掉一个影响小的指标，由此每个类别中算出3 个重要指标，进而采用EM 算法分别对两类指标进行聚类分析，不断迭代，当数据趋于收敛时，将所有站点的结果类型各个百分比输出。

下面分别是根据第一类、第二类指标聚类的12 个站点样本的数据展示，如表5、表6 所示。

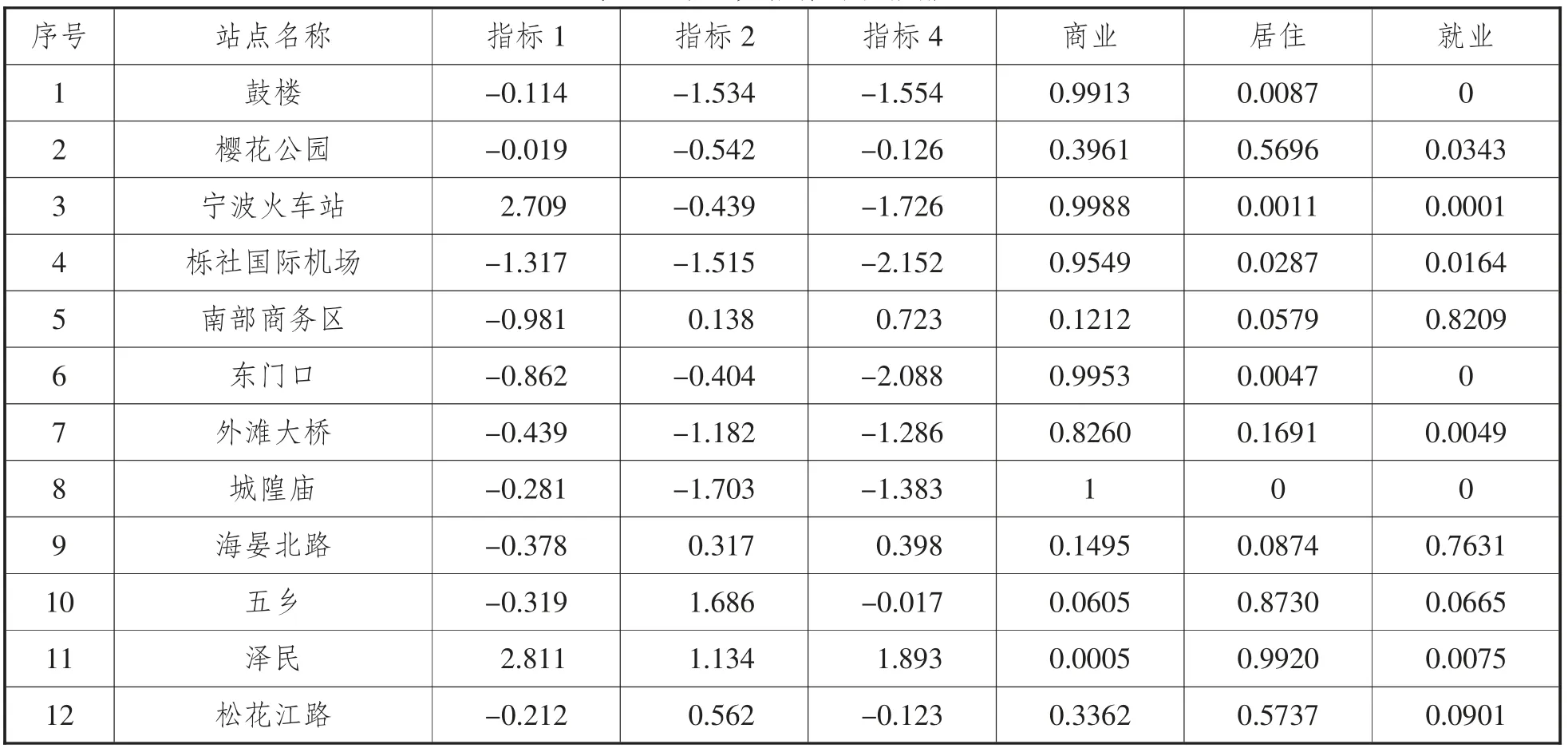
表5 第一类指标的数据输出

3.4 实验结果

图5、图6 分别是根据第一类、第二类指标聚类的所有站点的三维聚类效果图。

本次实验对宁波的64 个站点进行了研究，由于站点数量有限，聚类的结果不是特别明显，但是根据两类指标的聚类结果，得出了每个站点在3 种结果导向型中各自的百分比，2 种结果虽然百分比的数字不同，但是都是有着各自的指向型。根据结果将所有站点聚成6 类，第一类商业导向型，如东门口、外滩大桥、城隍庙、宁波火车站等；第二类居住导向型，如泽民、五乡、云霞路等；第三类就业导向型，如海晏北路、南部商务区、世纪大道等；第四类商业、居住导向型，如樱花公园、舟孟北路等；第五类商业、就业导向型，如福明路、江厦桥东等；第六类就业、居住导向型，如藕池、宁波大学、孔浦等。

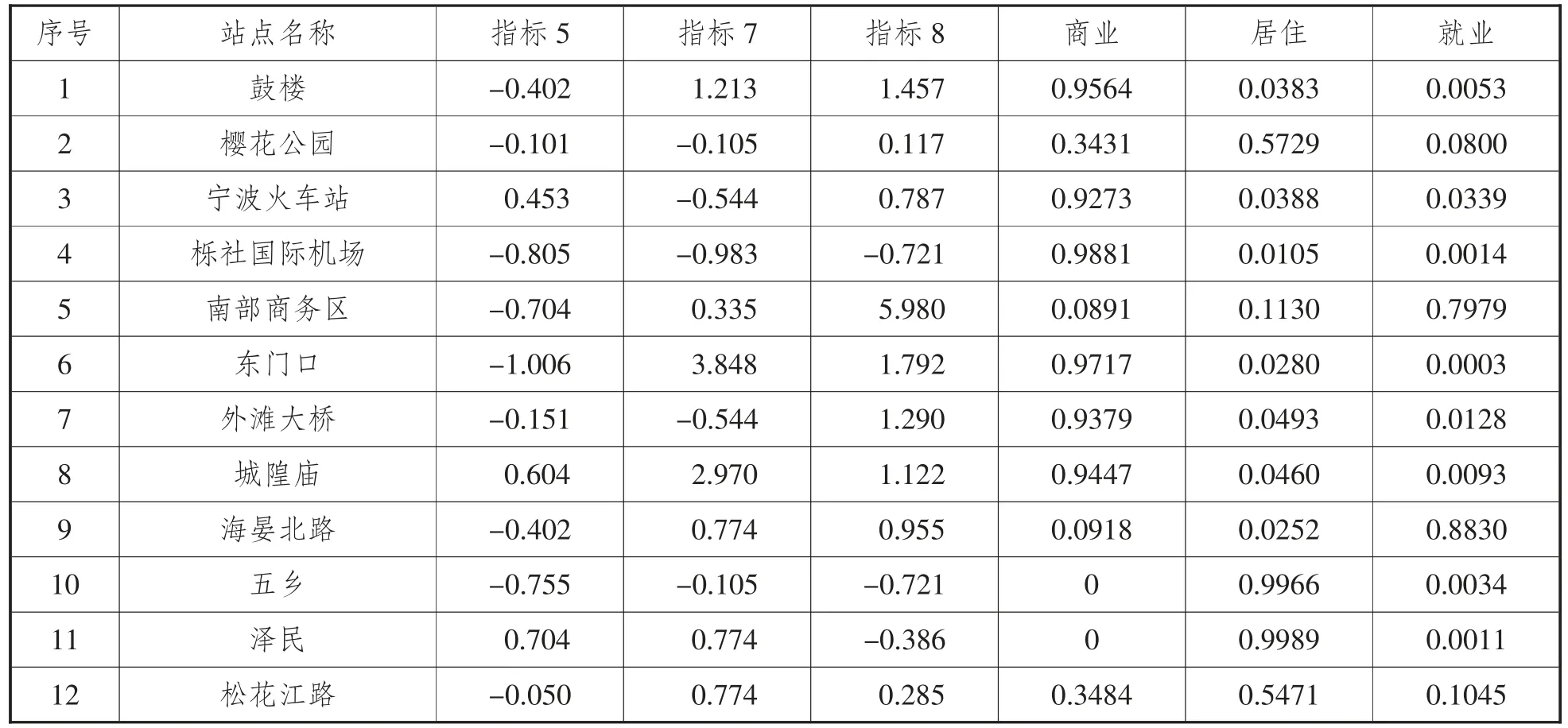
表6 第二类指标的数据输出

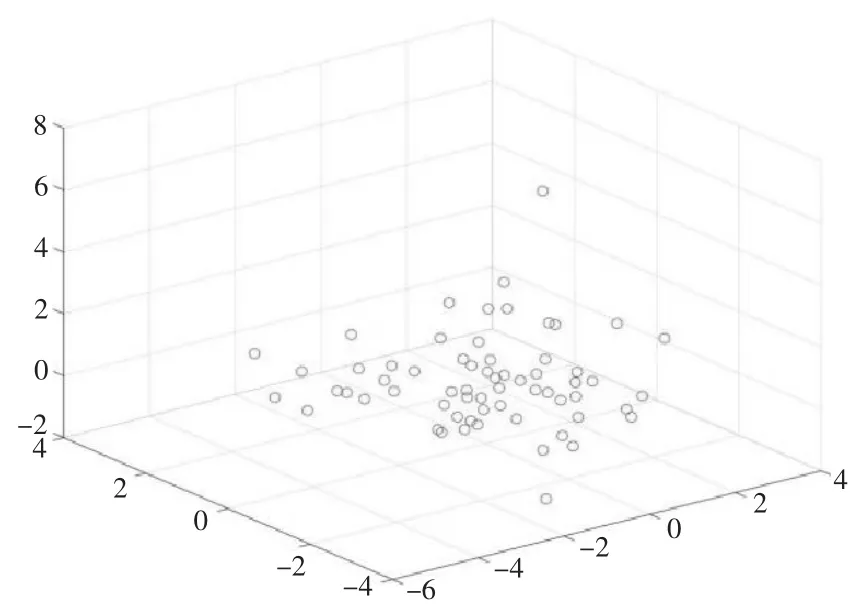
图5 所有站点聚类的三维图

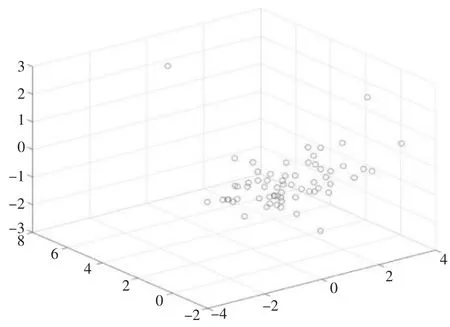
图6 所有站点聚类的三维图

4 结 论

城市轨道交通的发展为宁波市的长远规划打下了基础，使得城市框架更加平衡，将全市6 个区紧密联系起来，解决了交通污染的问题，方便了人们的日常出行，也避免采用限牌的策略。本文采用了贝叶斯推断的EM 算法对宁波市64 个地铁站点进行分级。研究表明：（1） EM 算法具有一定的局限性，当指标过多，或者是数据缺失的时候，不能很好地进行数据处理，当我们采用贝叶斯推断后，可以先将指标进行分类，根据不同类别，输出结果，再进行分析。（2） 根据聚类分析输出的结果数据可知，本文可以将宁波所有地铁站点分为6 大类：居住导向型；就业导向型；商业导向型；商业、居住导向型；商业、就业导向型；就业、居住导向型，也证实了贝叶斯推断的EM 算法在处理此类交通指标数据问题方面的有效性。（3） 对于地铁站点的价值研究也是一个不断探索的过程，随着指标的增多、城市的发展、地铁线路的增加以及数据处理技术的革新，对站点的研究也会处于一个不断优化的过程中。而本文研究主要是为了对目前的站点进行更加科学地分级，为城市轨道交通的下一步研究奠定了理论依据；促进了广告、通信、商业和新经济的发展；有助于进一步了解城市空间格局和社会特征。