基于遗传算法的公铁水多式联运路径优化问题研究

范方玲子，王茂春，陈厚春 （贵州大学 管理学院，贵州 贵阳550025）

0 引 言

物流运输方式由公路、铁路、水路、空运及管道等5 种方式组成，5 种运输方式在技术上、经济上各有长短，都有适宜的使用范围，每种运输方式单独运用很难实现节约资源、降本增效。随着我国经济不断发展以及布局网络技术的不断深化，多式联运通过把传统的、单一的运输方式进行择优组合，充分利用了各个运输方式现有的设施设备，实现了运输过程中的资源整合，有利于运输过程中的可持续发展及达成规模经济中降本增效的目的，同时提高了物流行业竞争力。特别是通过公铁水多式联运路径优化，构建以运输时间最少、运输线路距离最短、运输成本最低的公铁水多式联运模式，对于物流企业节约资源、降本增效意义重大。

多式联运的优化问题受到了很多专家学者的关注，从多个方面进行了研究。谢楚楚等（2018） 基于“一带一路”背景下中欧运输通道的多式联运运输网络构建及算法研究[1]。于雪娇等（2018） 基于运量不确定的前提下构建以节点作业时间窗和客户满意度为约束的多式联运路径优化模型，并提出符合节点时间及提升客户满意度的解决措施[2]。梁晓康（2017） 在以提高铁路集装箱运输效益的前提下，构建多式联运路径优化的线性规划模型[3]。范志强等（2011） 建立了更加符合实际的带软时间窗约束的多式联运路径优化数学模型，并用遗传算法找出符合条件的最优解[4]。李玉民等（2017） 为解决运输通道路径优选问题，在综合分析中欧班列集装箱运输基础上，构建中欧集装箱多式联运路径优化的多目标优化模型，提出中欧班列路径选择的指导性方案[5]。朱汉民等（2018） 从制度效率等方面探究我国集装箱多式联运对物流运输效率的影响程度及因素，构建集装箱多式联运效率评价体系[6]。诸葛恒英等（2017） 探讨我国多式联运运单推广运用策略，提出集装箱多式联运运单单一架构[7]。张哲辉等（2018） 分析集装箱铁水联运发展现状及存在问题，提出促进集装箱铁水联运的发展路径[8]。冷建飞等在研究多元线性方程中运用了统计学等原理求解[9]。秦凡等以顾客满意度最高为指标构建参数模型[10]。张大斌等运用遗传算法解决铁路运量预测的模型[11]。但是，从时间、距离、费用为约束条件，且应用遗传算法求解，探寻路径优化方式这方面的研究鲜有学者涉及。

1 多式联运路径规划影响因素分析

自2017 年1 月我国颁布了《关于进一步鼓励开展多式联运工作的通知》以来，标志着我国在运输模式的选择和发展上，多式联运有着重要的地位。近年来我国发展多式联运发展的现状表现为：（1） 集装箱公铁水多式联运的增速稳定保持在10%左右；（2） 随着多式联运示范工程在全国开展，16 家以多式联运为主的物流示范企业共开通了140 余条多式联运线路；（3）在2017 年中，开展多式联运的企业多达700 家，集装箱运输量超过60 万TEU；（4） 与单一公路运输方式相比，降低煤炭资源40 万吨，降低社会物流成本超过50 亿元。

可见，公铁水多式联运在物流中占主导地位，其中的联运线路是决定物流成本的关键。因此，本文以运输时间、运输距离及运输成本3 个影响因素为主，分析多式联运的路径规划，作为变量因子及衡量构建的路径是否合理的判断依据。

1.1 运输时间

多式联运过程中包含两种运输时间，第一种为发生在不同运输方式之间的在途消耗时间；第二种为在某个节点经停衔接下一种运输方式所需的物资搬运、装卸等所消耗的时间。在这两种运输事件发生过程中，若存在设施设备的维修、桥梁及铁路的改造时所发生的时间都需计算进总运输时间。无论是对于物流企业还是客户来说，运输时间的消耗也就是经济效益的流失，所以在绝大部分评价多式联运路径规划时都会把运输时间作为评价的重要参数之一。因此，最优的多式联运路径选择方案应消耗的运输时间最少。

1.2 运输距离

运输距离是多式联运路径中各个转换节点之间的里程数之和。运输距离的多少与运输时间和运输成本的消耗成正比，也就是说运输距离增大相应的运输时间会增长，投入在运输过程中的成本也会增多。所以在进行多式联运路径优化过程中会优先选择运输距离较短的方案。

1.3 运输成本

运输费用是指在物件实际位置改变或发生实际位移时，物流企业或客户所承担的全部费用。在多式联运过程中，运输费用一般包含由路径线路、运输方式及节点衔接过程中的换装技术决定的4 个部分的成本组成，即各个运输方式所需的过路费、燃油费；在某节点经停的换装费；运输工人的人工费；设施设备的使用维修成本。

2 多式联运路径优化模型的构建

2.1 问题描述和假设

2.1.1 问题描述

假设有一批物件以集装箱为单位需从A城市运往B城市，有若干节点，在整个运输过程中采用了由公路运输、铁路运输、水路运输组成的多式联运的运输方式。在整个线路规划中，充分考虑到降低物流企业的投入成本、提升运输效率、提高客户满意度，从而得到基于多方面因素的多式联运路径优化方案。

本文将选取时间、距离、成本3 个方面的影响因素构建多式联运路径优化方案。

假设多式联运随机路径布局网络图如图1 所示。

从图1 布局网络图可见，从城市A去往城市B会经过C、D、E3 个节点，各个节点之间都可选择公铁水3 种不同的运输方式，可

根据节点之间的运输距离、3 种运输方式可能消耗的运输时间和运输成本进行对比，最后择优组合不同运输方式完成由A至B的多式联运运输方案。

图1 多式联运随机路径布局网络图

2.1.2 模型假设和变量

多式联运过程主要包括运输和中转两部分。在整个运输过程中各个运输方式的费用及其所消耗时间都会计入总的运输成本和运输时间中，运输距离将根据相邻换装节点及转换的运输方式不同而改变。在运输过程中从起始点至终点会有很多种路径，可通过比较上述影响因素的经济效益择优选取某一运输路路线。

（1） 模型假设

①每两个节点之间最多转换一次运输方式。

②整个多式联运过程中运量保持不变，即在各个中转点不对运量进行增减操作。

③不考虑运输过程外产生的任何成本。

④对于在某节点转换的不同运输方式来说，相邻节点的同一种运输方式运输弧只有一条。⑤同一个节点物件最多经过一次。

（2） 模型变量

A=｛a1，a2，a3｝是不同运输方式的集合，其中a1代表公路运输，a2代表铁路运输，a3代表水路运输；

B=｛b1，b2，…，bn｝是多式联运路径节点的集合，bij为节点i至节点j运输；

φ（i）=｛bi|eij∈E｝为节点bi的外邻节点集合，η（i）=｛bi|eij∈E｝为节点bi的内邻节点集合；

E代表多式联运两节点之间路径线段的集合，eij为节点i至节点j之间的线段；

t为运输时间，tijai代表物件由运输方式i通过节点i至节点j的在途运输时间；

c为运输成本，cijai代表物件由运输方式i通过节点i至节点j发生的运输费用；

d为运输距离，dijai代表物件由运输方式i通过节点i至节点j的运输里程；

δbiai→j代表物件在节点bi由运输方式ai转换为运输方式aj所需的换装时间；

wbiai→j代表物件在节点bi由运输方式ai转换为运输方式aj所需的换装费用；

μbiai→j为一组（0，1 ）变量，其中μbiai→j=1 代表物件在节点bi满足运输方式由ai转换为aj的能力，否则μbiai→j=0；

（3） 决策变量

①xijai取1 时，代表物件由运输方式ai顺利通过节点i至节点j之间的路段，否则xijai=0；

②ybiai→j取1 时，代表物件在节点i有运输方式ai转换为运输方式aj，否则ybiai→j=0。

2.2 构建初始多目标优化模型

考虑多种影响因素，建立多式联运以运输时间、运输距离、运输费用为最小的目标函数的最优路径模型为：

（1） 最小运输时间

（2） 最小运输距离

（3） 最小运输成本

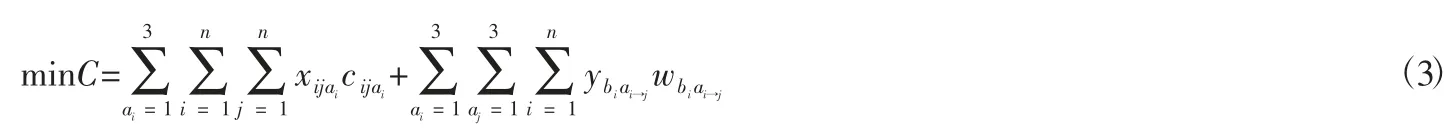
约束条件：

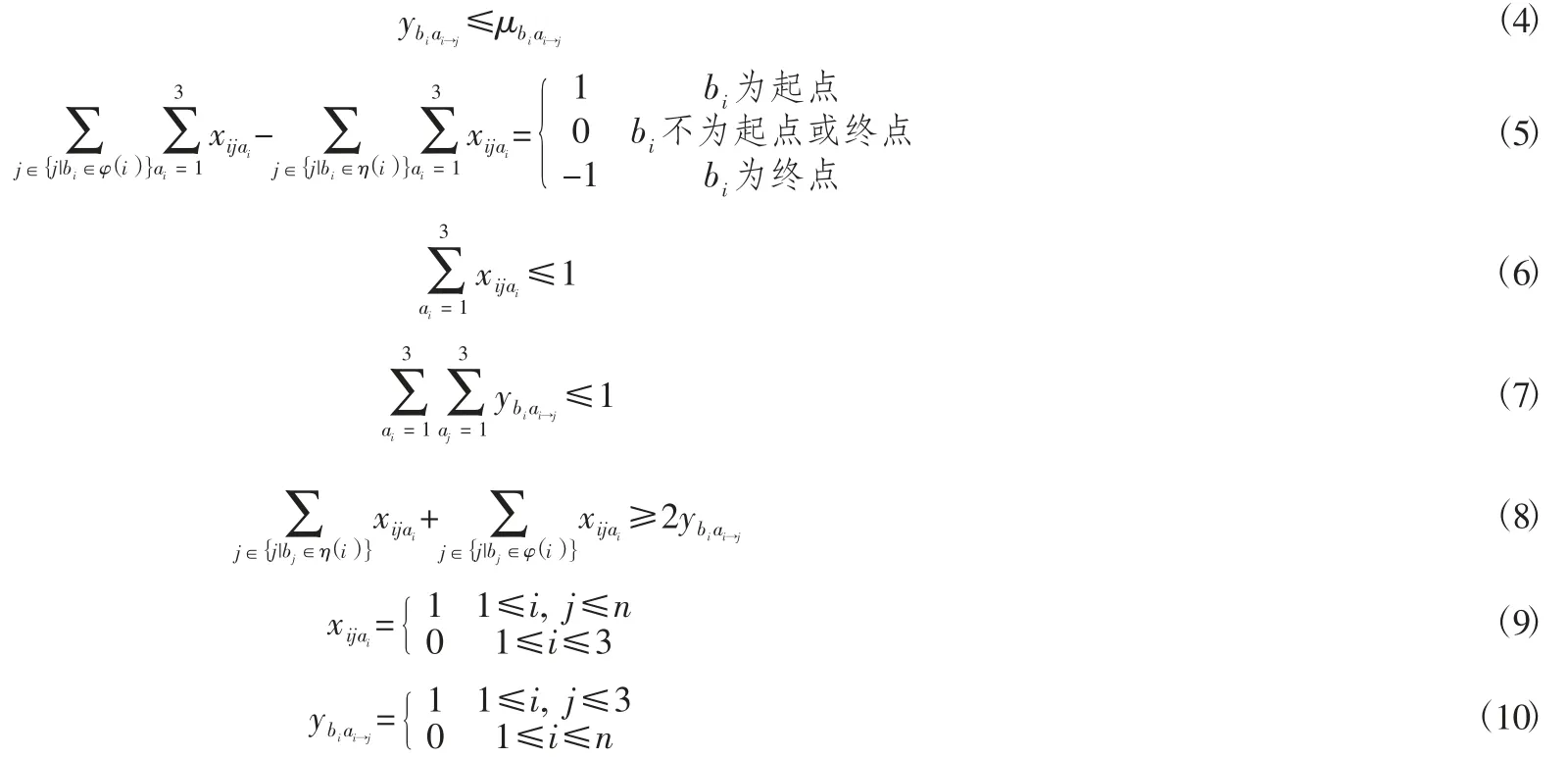
上述模型中，式（1） 为最短总运输时间优化模型，总运输时间包括物件在途运输时间及物件在某节点转换运输方式消耗的时间；式（2） 为最少总运输路径距离优化模型，在多式联运过程中，如何通过转换运输方式选择中转节点满足式（2） 是非常重要的评判指标之一；式（3） 是最少总运输费用优化模型，降低投入成本、提升效率、提高客户满意度是路径优化的目标；式（4） 约束了物件只能在具备换装能力的节点转换运输方式；式（5） 保证了某一中转节点的输出和输入量平衡；式（6） 约束了物件在其中一条路段中只能选择一种运输方式；式（7） 约束物件在某一节点最多只能进行一次运输方式的转换；式（8）保证了物件在多式联运运输中的连续性；式（9） 和式（10） 为（0，1 ）决策变量。

2.3 改进多目标优化模型

以上构建的模型为多式联运多目标路径优化模型，在求解多目标问题的模型时，一般采用线性加权的方式使多目标线性模型转换为单目标优化模型，有利于使每个目标模型都同时获得最优解。

基于此原因，本文将3 个多目标函数加入权重因子的形式改进为一个单目标函数优化问题，改进后的函数模型为：

式（11） 中，λi为优化目标函数fi的权重因子，λi∈［0，1 ］，通过λi给定的不同权重因子，改进优化模型都可获得对应的值。由于在多式联运优化路径方案中，运输时间、运输路径、运输费用的重要程度不同，所以在对λi做出如下赋值：

物流企业开展多式联运的目标除了降本增效外，还有提升客户满意度。在市场经济中，由于物流企业的高质量服务和客户对其的高度评价来赢得“回头客”或以此提升企业在市场中的竞争力，从而有更多的订单和客源，这对于一个企业是十分重要的。所以，在某项多式联运订单中，存在着更快更好地完成订单要求优先于仅仅是为了减少成本可能会降低服务质量的订单要求。因此，分别对运输时间、距离、成本进行敏感度的等价划分，如表1 所示。其中敏感度值越大，说明上述3 个因素的权重也越大。

由表1，可确定λi的取值为

表1 运输时间、距离、成本的第三度系数表

3 遗传算法求解模型

由于上述构建的是多目标多式联运路径优化模型，在模型中涉及到的变量较多，网络布局也非常复杂，因此采用遗传算法求解比较合适。遗传算法求解中，首先构建出适应度函数，其次根据适应度函数对种群中的每一个可行解进行评价，随后进行选择、交叉、变异操作，以此过程经过多次循环迭代，最终求出目标模型的最优解。

多式联运路径优化模型的遗传算法求解过程分为以下几步：

（1） 编码与解码：本文对模型的决策变量xijai和ybiai→j进行二进制编码，区间为［0，1 ］。通过编码公式确定二进制的编码长度；再根据解码公式对二进制进行解码，其中通常在算例时为了方便会以二进制转化为十进制的公式来计算所有个体适应度函数值。

（2） 初始种群：在确定编码方案后，通常会采用随机方法生成若干个体的集合，这集合称为初始种群。

（3） 适应度评价：对初始种群中，每个个体是否为可采用的可行解用适应度函数值Fi来评价，适应度函数值越大，则个体解越好，即可进行下一步运算中；反之，则淘汰。

按照构建的3 个多目标路径优化模型，通过权重因子将3 个函数转换为单目标函数模型进行求解。由于3 个多目标函数分别是针对时间、距离、成本构建的，所以变量单位都不统一，本文需对模型进行无量纲化处理。

根据每代遗传个体来说都可由3 个目标函数得到3 个可行解，因此分别对每个目标函数值进行无量纲化运输时间同理可得运输距离和运输成本，由此可得适应度函数为

（4） 选择运算：选择操作的任务就是从经过适应度评价后保留下来的父代群体中按照“轮盘赌选择方法”，选择出一些个体遗传到下一代群体中。其中，“轮盘赌选择方法”的基本操作原则是父代群体中每个单一个体的适应度函数值越大，则被选择遗传到下一代的几率也就越大。选择算子的概率为

（7） 终止运算：假设本文选取最大迭代数G=50 为终止条件，在达到终止条件前，持续进行若干次连续迭代，达到第50次迭代后终止迭代循环，从历次迭代中找出最优解的编码串并解码得出最优可行解及目标函数值。

4 算例分析

以贵州开磷物流公司多式联运路线为例，假设贵州开磷物流公司需从息烽站开磷智慧物流园为起始点运输总计100t 的5 个20 英尺的集装箱货物，运至东北地区销售。这其中，开磷智慧物流园作为起始节点A，中转节点B共3 个，中转节点C共3个，终止节点D有1 个，总共8 个节点，如图2 所示。根据上文构建的模型与遗传算法的应用，实现贵州开磷物流公司多式联运的路径优化，以选择出时间、距离、费用最优的线路。

为了方便得出目标值，算例中所用到的数据都根据贵州开磷物流公司实际数据为基础设定，假设公铁水3 种运输方式都以柴油供给，在铁路与水路转换的过程使用公路运输作为衔接，东北地区以沈阳为节点。从图2 中可看出，运输线路大体分为5 条，即（1） 息烽—东北； （2） 息烽—果园港—镇江港—东北； （3） 息烽—果园港—连云港—东北； （4） 息烽—武汉—连云港—东北； （5） 息烽—武汉—天津—东北。

以实际调研及参考相关文献、相关文件为依据设定的数据如表2 至表7 所示。

图2 息烽站至东北地区的运输网络图

表2 不同运输方式的运输成本、运输速度参数表

表3 第（1） 条线路的不同运输方式的运输参数

表4 第（2） 条线路的不同运输方式的运输参数

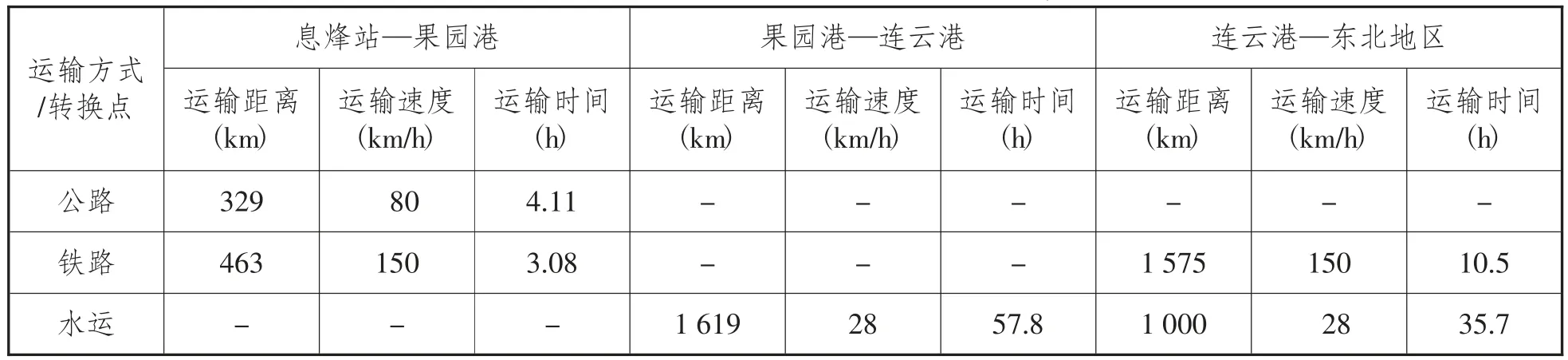
表5 第（3） 条线路的不同运输方式的运输参数

表6 第（4） 条线路的不同运输方式的运输参数

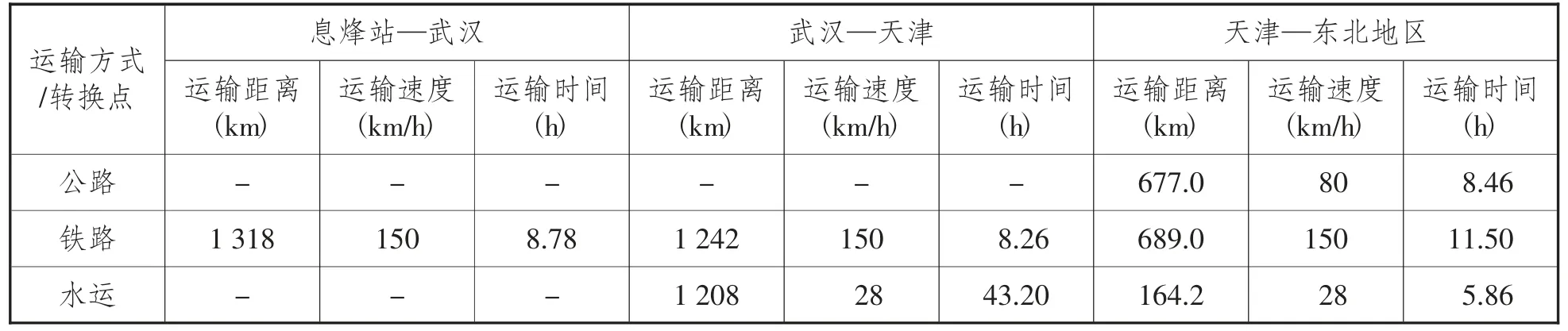
表7 第（5） 条线路的不同运输方式的运输参数

为了简化本案例的计算过程，算例中的权重因子的设定及敏感程度设定做了如下处理：λ1=7/ （7+ 5+3 ）=0.467；λ2=5/ （7+ 5+3 ）=0.333；λ3=3/ （7+ 5+3 ）=0.2。

本文采用Matlab 对案例模型进行求解，本案例中给定最大遗传代数gen=50，变异概率Pm=0.01，交叉概率Pc=0.97，运用上述设定的不同参数量，最终得到从息烽站运往东北地区的最佳路径。

根据图3，得出从息烽至东北地区多式联运运输方案中，第（4） 条线路为最优，即用铁路运输的方式从息烽站运至武汉站，在转换运输方式为水运运输从武汉至连云港，最后由水运从连云港运输至东北地区，其中的衔接皆为公路运输，算法求解值如表8 所示。

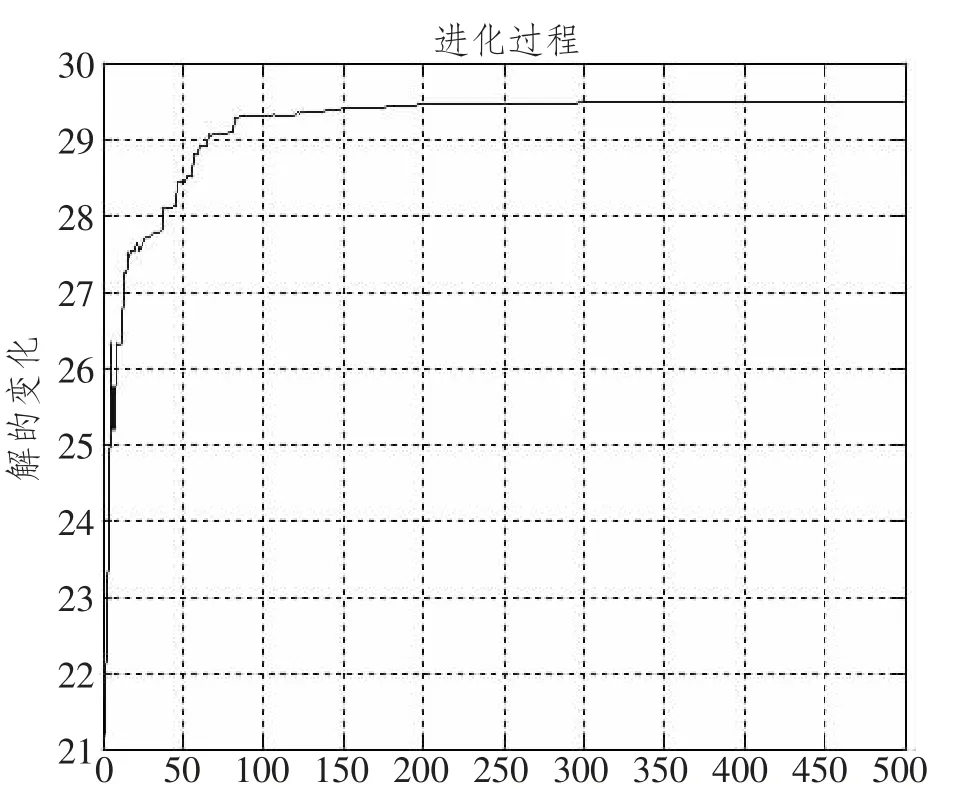
图3 迭代次数图

表8 最优多式联运方案

5 结 论

本文主要运用遗传算法求解了多式联运多目标最优路径模型，并且以贵州开磷物流公司的运输路线为例，提出由不同运输方式所组成的5 种运输路线，最后通过Matlab 软件对模型进行优化求解，最终得出运输时间、运输距离、运输成本这3 个不同权重的影响因素下的全局最优解，为物流企业开展多式联运运输提供了可供参考的依据。

由于实际数据及可参考资料的限制，模型未能求出更多的运输路线及运输方式的转换，所以当节点增多或遗传最大迭代数增多时该模型和算法还需一定的改善。