基于改进RBPF的激光SLAM算法研究

王馨阁，田宗强，陈文涛，张 雨，杨 光，王 伟，陈孟元*

(1.安徽工程大学 电气工程学院，安徽 芜湖 241000；2.安徽信息工程学院 电气与电子工程学院，安徽 芜湖 241000)

同步定位与地图构建(Simultaneous Location and Mapping,SLAM)是移动机器人研究中面临的主要问题，是实现移动机器人智能化亟待解决的关键技术[1-2]。基于卡尔曼滤波器的SLAM算法的提出有效地解决了最初的SLAM问题，但由于卡尔曼滤波应用范围仅局限于线性系统中，在移动机器人建图过程中遇到的大多是非线性非高斯系统，针对此种问题，基于卡尔曼滤波器的SLAM算法并不能很好地解决[3]。随着粒子滤波的出现以及非线性系统中粒子滤波的精度逐渐接近最优估计的事实，粒子滤波已经被大多数学者用于SLAM。其中Montemerlo[4]和Paskin[5]等提出了一种可以有效地解决SLAM问题的RBPF算法。目前，移动机器人实现自主定位与导航的基础就是依靠各种传感器，而激光传感器是最精确、最稳定的传感器之一,因此，激光SLAM成为最主流的自主定位导航方法。对于简单的室内环境来说，与视觉SLAM对比，激光SLAM在精度和稳定性上有着明显优势[6]。目前，基于粒子滤波器(Particle Filter,PF)，即PF-SLAM算法的激光SLAM算法，在实际应用中，环境中存在的大量路标会引起PF-SLAM算法状态向量“维数灾难”，导致求解计算过程十分复杂。文献[7]首次提出将Rao-Blackwellised粒子滤波器(Rao-Blackwellised Particle Filter,RBPF)，即RBPF-SLAM算法应用于解决SLAM过程中状态向量维数高问题。文献[8-9]认为基于RBPF-SLAM的算法可以分解为定位和建图两大部分。RBPF-SLAM算法的提出使得定位与建图过程中的计算量大为减小，为SLAM的发展奠定了理论基础[10]。针对算法实时性效率问题，一种基于RBPF-SLAM的Gmapping算法被提出，该算法的主要内容为利用高精度、高稳定性的激光测量数据可以改善提议分布的求解过程这一特性，使得改进后的提议分布与实际后验概率分布更为接近，进而提升算法的实时性[11]。另一方面，针对基于粒子滤波的SLAM算法的研究中相继被提出的主要为FastSLAM算法和GMapping算法[12]，两种算法在求解过程均利用了粒子滤波能够对多模态分布进行非参数处理的特性，获得与正确值更接近的状态解，从而提升建图效果，降低定位误差。但是，在求解过程中粒子滤波器SLAM的结果不一致，以及状态向量的不断扩张会导致内存消耗大，在进行状态估计时，由于后验概率的计算也会引起马尔科夫假设的误差累积，使得粒子滤波器SLAM算法受到很多限制[13]。

传统RBPF-SLAM算法在实际应用中往往需要大量的粒子。其主要原因一方面是在针对建议分布的计算过程中只考虑运动模型数据而忽略实际测量数据，引起估计值与观测值的误差较大，从而需要更多的粒子对误差进行拟合，但这一过程消耗了大量内存，降低了算法效率[14]。另一方面，在粒子滤波阶段，由于粒子样本贫化问题，大量粒子的数据不可用，降低了SLAM定位精度和误差累计现象。对于此，Moral[15-16]等提出了一种自适应重采样方法改进粒子滤波阶段的重采样贫化问题以及降低使用粒子的数量。

在此基础上，利用高精度的激光雷达传感器数据来改进建议分布函数和修正里程计读数，提升有效粒子集合的粒子数量。同时，针对粒子退化问题，采用一种自适应重采样机制约束重采样进程，避免粒子滤波过程中的粒子贫化问题。以机器人操作系统(ROS)为基础模型，进行机器人平台实验和仿真实验验证所提算法的有效性。

1 算法研究

1.1 基本RBPF-SLAM算法原理

SLAM的关键思想是求解后验概率p(x1∶t,m|z1∶t,u1∶t-1),其中z1∶t=z1,z2,…,zt表示机器人自主观测数据信息；u1∶t-1=u1,u2,…,ut-1表示里程计数据信息；x1∶t表示移动机器人的估计运行轨迹；m表示环境地图。RBPF-SLAM算法将SLAM问题划分为定位和建图两大部分，以此来降低采样过程中状态空间维数扩张问题，达到简化计算过程的目的[17-18]。其中，基于环境地图和机器人运行轨迹x1∶t的联合后验概率分布，即

p(x1∶t,m|z1∶t,u1∶t-1)=p(m|x1∶t,z1∶t)·p(x1∶t|z1∶t,u1∶t-1),

(1)

式中，右侧为两个独立的后验概率乘积，其中p(x1∶t|z1∶t,u1∶t-1)为机器人运行轨迹的估计后验概率；p(m|x1∶t,z1∶t)为环境地图的后验概率；在解决SLAM问题中，这样的概率分解可以先计算机器人的运行轨迹，之后在已知机器人运行轨迹的情况下计算并更新当前的环境地图。每一个粒子代表一条可能的机器人运行路径。

RBPF-SLAM算法的运行步骤具体如下：

(3)计算权重：根据权重采样原则，计算每个粒子分布单独的重要度权重ω(i)，即

(2)

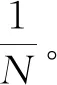
1.2 激光雷达扫描测量模型

二维激光雷达的测量为平面(这里不考虑其在z轴方向上的运动，即其扫描范围仅为平面),激光雷达的旋转中心设置在坐标系的原点，Neato XV-11激光传感器的正面被定义为坐标系的X轴。坐标系遵循左手法则。

激光雷达扫描测量模型如图1所示。由图1可知，P为观测点；d是P点距离传感器的距离；θi是方位角(即激光束的发射角度)。由此将坐标系转换为笛卡尔坐标系来处理原始数据，然后收集激光扫描数据的集合为B={(xi,yi)|i=1,2,…,N}，坐标变换如式(3)所示。

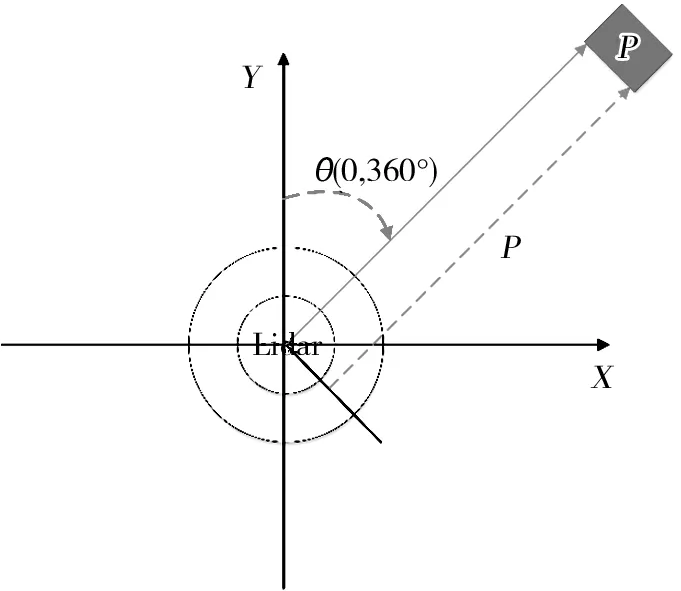
图1 激光雷达扫描测量模型

(3)

2 改进RBPF-SLAM算法

2.1 改进建议分布函数

单独将里程计运动模型作为提议分布时，可以简化计算，但由于里程计在运动过程中易受外部环境干扰，在进行重采样过程中会出现粒子退化现象，导致重要粒子的丢失，激光的分布相比里程计分布更接近目标分布。因此，为了能够充分覆盖高观测似然区域，引入较为精确的激光雷达数据对建议分布函数进行改进。通过在观测概率峰值附近选取K个值来模拟建议分布，降低粒子数目减少计算量。利用扫描匹配筛选出概率大的区域后，对此区域进行重采样，利用近似化正态分布实现K个粒子概率值模拟出的改进建议分布。

SLAM要解决的问题是由控制数据u1∶t和观测数据z1∶t来求位姿和地图的联合分布p(x1∶t,m|z1∶t,u1∶t-1)，为了改进提议分布，研究使用最近一次的观测值计算一个粒子的采样数据。然后，利用该粒子在生成下一代粒子时负责观测最近代数粒子的权值，从目标分布中获得机器人的位姿估计，通过应用贝叶斯定律展开得到改进建议分布为：

(4)

扫描过程中的粒子分布可近似表示为高斯函数：

(5)

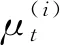
(6)

(7)

(8)

在扫描匹配后，粒子分布改变，需要重新计算粒子权重，选取最接近相应扫描的最大概率样本粒子作为近似xj，根据前后2帧激光雷达扫描数据进行匹配，对移动机器人的运动模型数据进行修正，粒子权重变为：

(9)

改进完建议分布后需要进行重采样，在重采样之前，利用迭代最近点算法(Iterative Closed Point,ICP)对粒子进行扫描匹配，求解最小误差，提高位姿估计解算精度，迭代公式表示为：

(10)

2.2 改进自适应重采样

在重采样滤波阶段，出现的粒子权重退化现象主要表现为：当第一代粒子经过N次迭代后，部分粒子的权重开始变小，甚至出现权重为零的现象，其中仅有少部分粒子的权重较大。因此，引入有效粒子数Neff[19-20]估计当前粒子集对目标函数的近似程度，伴随着滤波采样的进行，无效采样粒子数目逐渐增加，将会浪费大量的计算资源和内存消耗，使得估计时间增加，定位精度低。因此，引入有效粒子数Neff来衡量粒子权值的退化程度，即

(11)

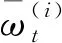
(12)

式(11)表示权重大的粒子过多或权重小的粒子过多，粒子权重之间差距越大，表明在重采样过程中粒子所占权值退化现象越严重，当采集的有效粒子数低于预先设定的阈值时，保留权值大的粒子进行重采样。

采用一种自适应的重采样方法来保持粒子的多样性，防止粒子退化现象的发生，其主要内容为在重采样阶段，保持对权重较高和权重较低的粒子进行重采样，对中等权值的粒子进行保留，具体步骤如下：

步骤2 对重采样过程中每个粒子被复制的次数ni进行计算统计，并按照从高权重粒子群到低权重粒子群的顺序排列，中等权重粒子群直接保留。建议分布函数中每个粒子被选择的概率为：

(13)

式中，rank(i)表示权重改变后重新排列后的粒子序号；arank,brank为常数系数。根据式(13)确定，arank=2-brank,1≤brank≤2，取值为：

(14)

(15)

根据以上所述过程执行重采样，如果当前粒子被复制的总次数∑ni<(NH+NL)，则将权重由高到低的粒子被复制的次数进行增加，最终达到∑ni=(NH+NL)；如果∑ni=(NH+NL)，则减少权重由低到高的粒子被复制的次数，达到∑ni<(NH+NL)，保持粒子总数不变。改进提议分布和自适应重采样后的RBPF-SLAM算法流程图如图2所示。

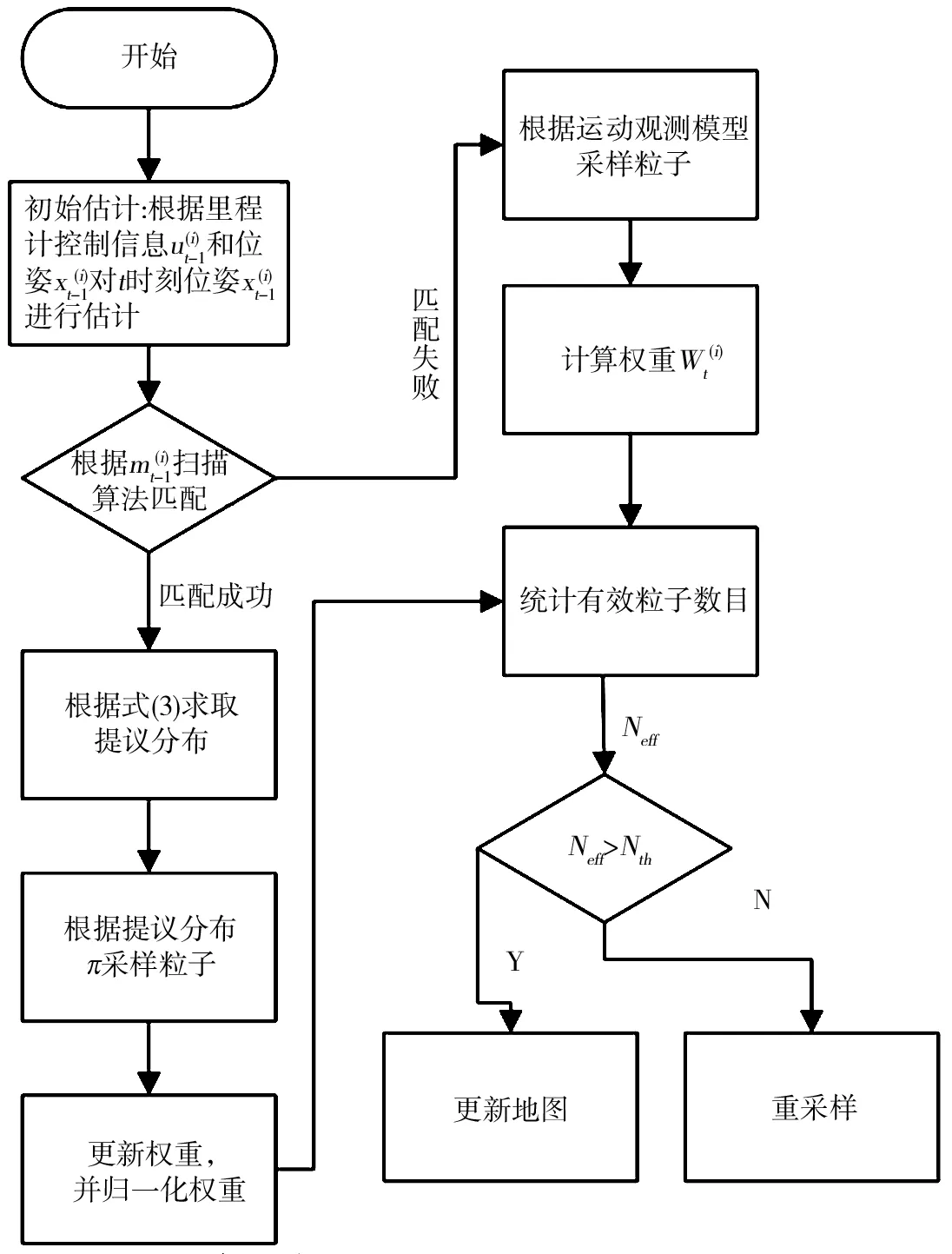
图2 改进RBPF-SLAM算法流程图

3 实验结果分析

3.1 实验平台

实验硬件平台为配置有里程计和激光雷达的“旅行者Ⅱ”移动机器人，同时搭载了一台装有Ubuntu 12.04操作系统的笔记本电脑。激光雷达RPLIDAR AI分布于机器人顶部四周，里程计则位于移动平台内部，移动机器人平台如图3所示。机器人以0.5 m/s的速度匀速移动，进行在线实时构建地图，并用RVIZ显示地图。

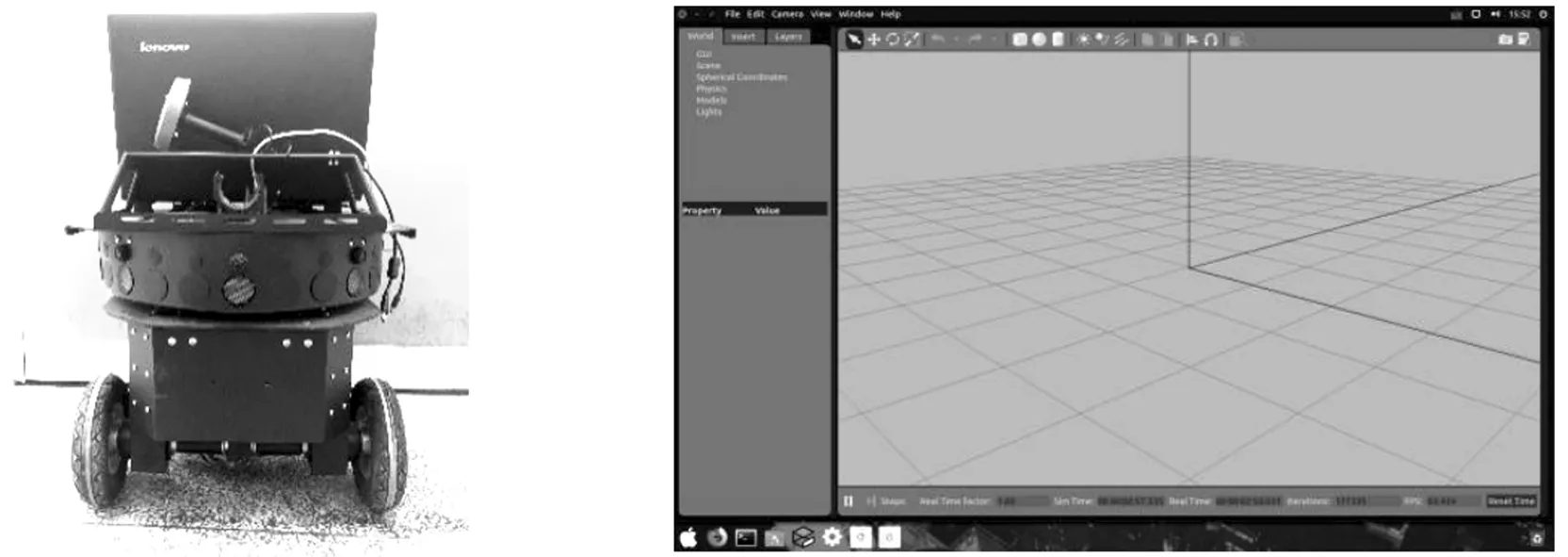
图3 移动机器人平台 图4 Gazebo仿真环境界面

3.2 基本建图

实验环境地图大小为10 m*10 m，Gazebo仿真界面如图4所示。搭建的虚拟仿真环境效果图如图5所示。采用传统RBPF-SLAM算法构建的室内地图如图6所示，改进算法构建的室内地图如图7所示。在图7中3个缺口表示未探测区域，其中被深灰色线条包围的区域表示扫描到的障碍物区域。经过反复实验，在算法滤波定位阶段，样本粒子数目设置为30，效率和建图效果更佳。从对比效果来看，相对于传统的RBPF-SLAM算法，在提出的改进算法中，可以根据激光雷达和里程计数据优化提议分布，改进的算法使用更少的粒子数目可以创建出精确度更高、效果更好的环境地图。

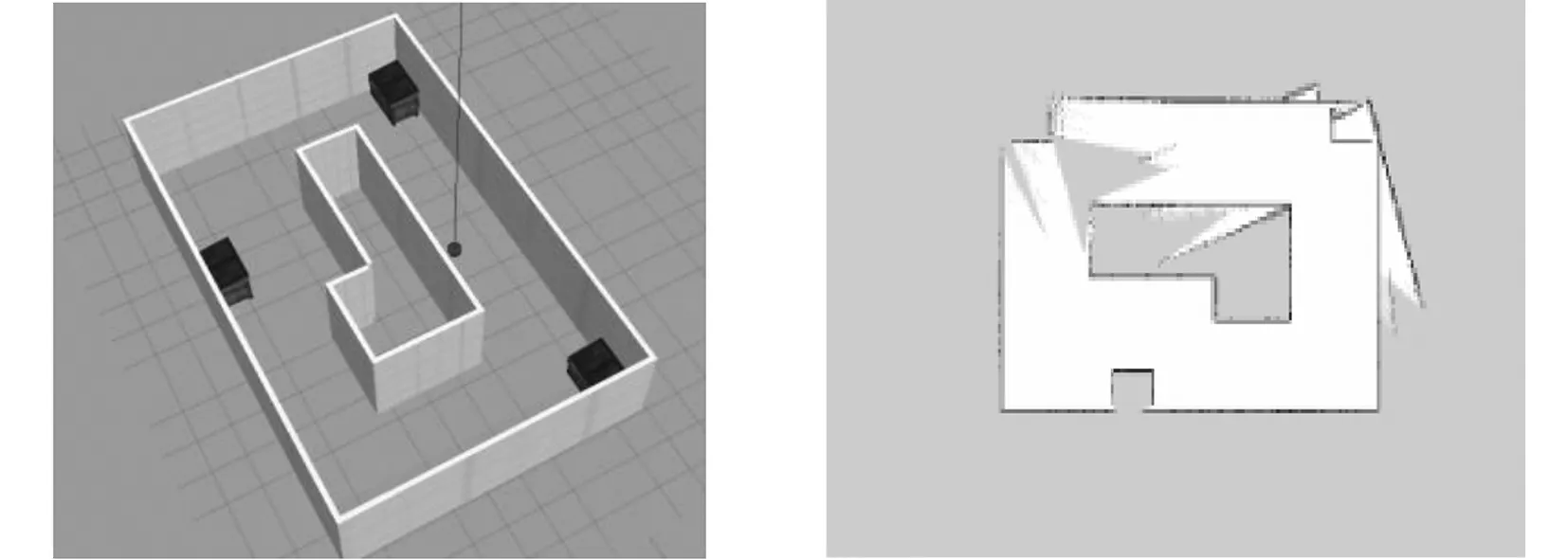
图5 虚拟仿真环境 图6 传统RBPF-SLAM算法

图7 改进RBPF-SLAM算法

3.3 算法对比实验

在实际工作环境下，移动机器人所面临的比搭建的理想化地图更为复杂，所包含的具有显著特征环境信息也较丰富，且在运行过程中会受到如行人、移动障碍物等的影响。对于此种情况，分别用传统RBPF-SLAM方法和改进的算法进行定位和构图实验，以此来分析改进算法的有效性。

利用传统算法构建的部分办公区域栅格地图如图8所示。改进算法构建的部分办公区域的栅格地图如图9所示。在构图扫描匹配过程中，轮式机器人的运动轨迹如图10所示。从实验结果可知，研究改进RBPF估计轨迹和真实值一开始相差较大，但最终会跟随在真实值附近，具有良好的跟随性，而传统算法一直出现漂移现象且误差越来越大。相比于传统RBPF-SLAM方法，在环境结构复杂的场景中，改进的RBPF-SLAM方法构建的走廊及办公区域栅格地图基本无失真且构建的栅格化地图较清晰，定位精度更高。

图8 传统RBPF-SLAM算法构建办公区域地图 图9 改进RBPF-SLAM算法构建办公区域地图

图10 办公区域运行轨迹对比

3.4 结果分析

为验证改进算法能降低运行轨迹的误差且减少所需粒子数，在2D LIDAR数据采集中，对改进算法进行反复实验，真实轨迹与测量轨迹的一致性地图如图11所示。轮式机器人运行误差分析如图12所示。从图11中可以看出，初始运动时粒子的真实轨道和预测轨道相差较多，但运行一段时间后，预测值逐渐向真实值靠近，并在真实值附近跟随，具有良好的预测效果。在最开始运行时，粒子群误差和测量误差的差值较大；随着运行时间的增加，粒子群误差逐渐向测量误差靠近，两者误差值逐渐变小，且一直保持在较低水平。

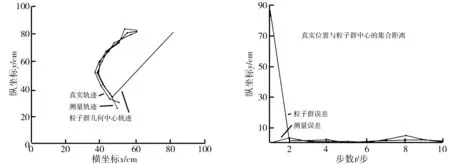
图11 粒子运行轨迹 图12 运行误差分析

分析比较改进算法与传统算法在运行时间上的性能对比，在实验过程中分别采用两种算法进行了5次实验，对实验结果取平均值作为统计值，性能对比如表1所示。由表1可知，改进算法所需粒子数远小于传统RBPF-SLAM算法，构建地图所需时间也比传统RBPF-SLAM算法有较明显的缩短。

表1 创建地图性能对比表

4 结论

研究对基于RBPF的激光雷达SLAM算法进行了研究和优化。通过运动里程计与RPLIDAR激光测量相结合，校正基于里程计测量值的建议分布函数，调整粒子权重提高了有效粒子数目；同时，通过自适应重采样的方法重新估计粒子的权重，得到精确的栅格地图，有效地缓解了由于重采样带来的粒子退化问题，改进了粒子滤波在地图估计中的不足。仿真结果表明，通过将运动里程计信息和激光测量数据相结合并通过自适应重采样的方法，解决了粒子权重退化问题，优化后的激光SLAM算法的建图和定位精度均得到提高。