一题多解：基于概念教学的应用技巧

江苏省南京市华电中学 张 宁

一题多解，就是根据不同思维，运用不同方法，解决相同习题或得到同一道习题的答案，这是解答数学习题常用的手段。一题多解的价值不仅仅在于解决习题答案本身，更多的还体现在提升学生学习的兴趣，开展合作学习，开发学生的智力，激发学生的思维，从而提高学生的认知与解决问题的能力。数学概念是反映一类事物在数量关系和空间形式方面的本质属性的思维形式，在该类对象的范围内具有普遍意义。而数学概念教学则是中学数学教学的重要内容之一，通过数学概念的教学，不仅可以让学生了解数学概念的本质，还可以延伸或拓展数学概念的内涵和外延，更加理性地了解概念的表述、分类，从而在概念系统中进一步提升学生对数学的认知。

一题多解与概念相结合的运用可以促进学生数学学习的思维、兴趣的发展以及对数学概念的认知，这无疑对数学教学以及提升学生数学素养具有很高的价值。为此，我们以一道几何证明题为例，进一步分析一题多解和概念教学的过程。

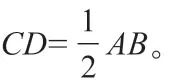
求证：△ABC为直角三角形。

∴AD=BD=CD，

∴△DAC和△DBC都是等腰三角形，

∴∠A=∠ACD，∠B=∠DCB，

∴∠A+∠B=∠ACD+∠DCB=∠ACB。

在△ABC中， ∠A+∠B+∠ACB=180°，

∴∠ACB=90°，∴△ABC为直角三角形。

这种解法用到了三角形内角和定理。

证法二：如图2，作DE⊥BC，E为垂足，故∠DEB=90°，

∴△ 和△ 都是等腰三角形，

∴∠A=∠ACD,∠CDE=∠BDE，∠A+∠ACD=2 ∠A。

而∠BDC=∠BDE+∠CDE=2 ∠BDE，又∠BDC=∠A+∠ACD，

∴2 ∠A=2 ∠BDE, 即∠A=∠BDE，∴AC∥DE,

∴∠ACB=∠DEB=90°，

∴△ 为直角三角形。

这种解法用到了等腰三角形三线合一、三角形外角等于不相邻两个内角的和及平行线的判定。

证法三：如图3，延长CD到点E，使DE=DC，连接AE和BE。

∵AD=BD，

∴四边形ACBD为平行四边形。

∴CE=AB,故平行四边形ACBE为矩形，

∴∠ACB=90°，∴△ABC为直角三角形。

这种解法用到的方法是添补、构造平行四边形，用到了平行四边形的判定及矩形的判定。

∴AB是以D点为圆心，AD为半径的圆O的直径，

故∠ACB=90°，

∴△ABC为直角三角形。

这种解法用到的方法是构造圆，用到的概念有圆的定义、圆周角性质。

对一道几何题多种证法的分析不难发现，熟练运用概念是学生学好几何知识的关键。我们可以看出，一题多解尽管不断地改变解题方法，不断体现了思维的多变，但解题的本质属性却没有变，借此解题过程可以帮助学生打破僵化的局限于“标准”的思维模式，从而在概念的理解上避免片面化，这样学生就能够透过现象看本质，准确理解概念。

当然，几何概念是几何学的基础知识，几何概念的教学是培养学生数学素质及逻辑思维能力和空间观念的重要一环，同时我们必须清楚，如何讲透概念，对老师来说又是一个难点，因此还需要我们每一位教师进一步深入探索才能不断突破。