一种大规模时序语义网络中突发持续性事件搜索算法

孟天宇 李源 孙晶 刘金生

（北方工业大学信息学院 北京市 100144）

1 引言

真实世界中，社交网络，生物网络，交通网络等都是高度动态的,可以用图模型表示[1]。给定一个图G=(V,E,W,T), 其中顶点V 表示实体，E,W,T 是一个四元组（u,v,w,t）,u,v 表示两个实体，w 是u,v相互作用的时边上的权值,t 是u,v 相互作用的时间，涉及时间信息的图通常被称为时序图[2]。在分析大规模的时序网络中，事件的交互模式往往是突发的[3]，这里的突发表示事件在很短的时间发生。本文研究的是时序图中的突发持续子图，突发持续子图表示的是一个稠密子图在很短的时间出现，并且持续一段时间。换句话来说，我们旨在时序图中搜索出在很短时间内发生且具有持续性的稠密连通子图。在时序图中搜索出突发持续子图可以帮助我们应对生活中许多实际问题。例如，在紧急事件检测方面，突发持续子图可用于通信网络中紧急事件检测[4]，在商业协作方面，突发持续子图可以找到在商业协作网络中最亲密的合作关系，帮助我们找到新的商业机会[5]。目前为止，时序图中稠密子图挖掘问题[6,7,8,9]被研究者广泛的研究，该问题旨在找到时序图中所有的目标子图，但是当数据规模过大，这一问题将变得复杂，且发现效率较低，针对以上问题，本文提出了时序图中的突发持续子图（Burst Persistence Subgraph，BPS）模型。给定一个时序图G(V,E,W,T)查询点q 和正整数k，BPS 为时序图中的子图g，并且满足如下两个条件：

（1）图g 中所有节点满足其邻接点的度数与边上的权值的乘积之和在同一时间时刻增大，且乘积之和持续了一段相同的时间戳。

（2）图g 是一个与查询点q 连通的k-核图。使用BPS 定义时序图中的突发持续的稠密子图有以下优点：BPS 不仅找到在时间上具有突发持续性质的稠密子图，而且包含查询点q 的k-核算法的搜索效率较高，可以扩展到大图计算。

2 基本概念及相关定义

本节主要介绍一些基本概念及其符号表达，阐述了时序图的相关定义，并对要解决的主要问题给出具体定义。

2.1 基本概念

令G(V,E,W,T)来表示一个时序图，节点集V={ν1,ν2…νn},n=|V|,表示顶点的个数。m=|E|表示边和其对应权重的个数,s=|T|为时间戳的个数。每条边eϵE 是一个四元组（u,v,w,t）,v,u 是V 中的节点，w 是u,v 相互作用的时边上的权值，t 是u,v 相互作用的时间。W={w|（u,v,w,t）∈E},表示边上权值的集合。T={ t|（u,v,w,t）∈E},为所有节点之间存在联系时刻的集合。Nt(v)表示图G 在t 时刻下中v 的邻接点的集合，节点ν 在t 时刻下的度数为degt(v)，他对应的值为degt(v)=|Nt(v) |。

表2：数据源的实验参数

突发持续子图中节点有一些共同特征，这些节点的突发度较高且持续时间较长，接下来给出具体的相关定义来描述其属性。

定义1 (重要度)：图G 中一个点的在某一时刻的重要度在用Bt(v)来表示，其中v∈V

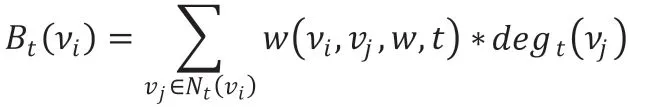
在t 时刻下，Nt(vi)表示节点vi 的邻接点集合，degt(νj)表示节点νj的度，w(νi, vj, w, t)表示νi, νj两点间的权值，节点νi的重要度与其邻接点的度数以及连接的边的权重成正相关。

定义2(时序子图)：给定时序图G(V,E,W,T)，在连续的时间间隔内，对于节点S⊆V 时序子图可以用GS(T)=(S,ES(T),WS(T),TS(T))来表示。接下来给出突发持续序列（Burst Continuous Sequence，BCS）的定义。

定义3(BCS)：给定BCS(q)={ti}来表示节点q 的突发持续序列。突发度用λ，持续度用α，持续性用γ，节点满足在某时刻重要度的增大的值大于等于λ，且在时间戳为γ内重要度的变化范围为[-α,∞]，则该节点在这一时刻满足突发持续。突发持续序列为满足突发持续的时间戳集合，在突发持续度序列定义的基础上，提出了一个候选子图（Candidate Subgraph,CS）的定义。

定义4（CS）：给定CS(q)表示包含查询点q 的候选子图。候选子图是满足时序图在时间戳γ+1 下包含查询点q 的静态投影图且图所有的节点具有突发持续性。接下来给出时序图中的突发持续子图（Burst Persistence Subgraph，BPS）的定义。

定义5 (BPS)：给定候选子图CS(q)，正整数k(k ≥3)以及一个查询点q，那么g 称为BPS,如果满足如下条件：

（1）g 是CS(q)的子图且是包含查询点q 的k-核子图；

（2）g 为满足条件（1）（2）的极大子图，也就是不存在g’∈G使得g⊆g’并且g’满足条件（1）。

2.2 问题定义

基于以上定义，本文给出了在时序网络网络中突发持续子图搜索的问题定义

问题1：给定时序图G(V,E,W,T)正整数k(k ≥3)和查询点q，首先找到找到节点q 的突发持续性序列BCS(q)，然后根据查询点的突发持续序列得到候选子图CS(q)，最后从搜索出BPS 子图结构。

接下来的章节，我们具体的阐述BPS 的搜索算法。

3 BPS搜索算法

本节讲述时序图中突发持续子图搜索问题，给定包含查询点q的时序图，从中搜索所有的BPS 子图。在搜索算法开始前，对时序图进行预处理，首先根据第二节的重要度定义得到查询点的重要度，其次确定参数λ，α，γ 后，得到查询点的突发持续序列 BCS(q)。接下来详细的介绍两种搜索算法。

3.1 QS-BPS算法

本小节的QS-BPS 算法，是基于普通事物队列的基础策略。首先计算候选子图CS(q),将CS(q)中节点度数小于k 的节点入队，其次将队列中节点出队，删除邻接点及相关边并更新节点度数,将节点度数小于k 的入队，直至队列为空，然后广度优先搜索找到与查询点q 连通的子图添加到结果集中，最后返回BPS 子图结构集C，结构集C 中包含所有可能的BPS 子图。

算法1：QS-BPS.

算法2：SP 算法.

3.2 KS-BPS算法

本节对上一小节的算法进行改进，提出了一种优化策略下的KS-BPS算法，首先计算候选子图CS(q)，其次对CS(q)进行求核分解,得到节点的核数，然后广度优先搜索找到节点核数大于k 且查询点q 连通的子图添加到结果集中，最后返回BPS 子图结构集C，结构集C 中包含所有可能的BPS 子图。

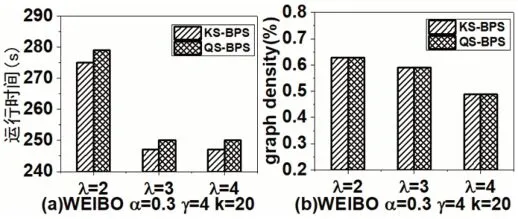
图1：不同参数λ 下的指标对比

图2：不同参数α 下的指标对比

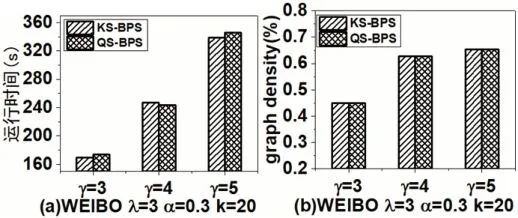
图3：不同参数γ 下的指标对比

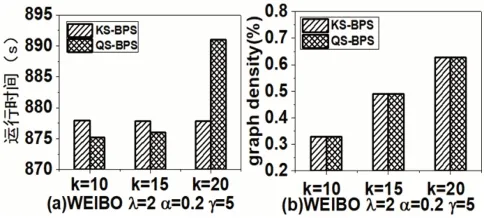
图4：不同参数k 下的指标对比

算法3：KS-BPS.

通过对CS(q)进行k-核分解，可以获取每个顶点的核数，为寻找k-核图做准备，core-number 算法的具体过程参见文献[10]。

4 实验结果与分析

为了有效的评估提出的算法，本实验用真实的微博数据集进行评估，数据集的详细统计信息汇总在表1 中，其中|V|表示顶点个数、|E|表示时序边数、|E’|表示静态投影边数、kmax节点最大核数、|T|表示时间快照的数量。WEIBO 是从微博上爬取的2019年12月1日到2020年4月17日的语义网络。时间戳单位是日。

4.1 实验参数设定

本文中的两个算法都涉及到了四个参数λ,α,γ,k。其中λ,α 作为时序参数用于确定节点的重要度的变化范围，γ 用于确定子图的最短持续时间，k 用于确定子图的结构内聚性，实验部分将各个数据源的需要的四个参数分别取三个值。数据源参数的取值信息如表2所示。

4.2 不同参数下算法有效性分析

由于不同的初始参数对算法的有效性和高效有影响，本节将进行不同参数下算法性能的对比实验，选用运行时间和graph density两个指标对算法的高效性和有效性进行评价，两个指标的具体概念如下：

（1）运行时间：本文提出的两个算法加上预处理的运行时间

（2）图密度graph density：用实际边数除以最大可能边数，即为图密度，当图密度越大时表示图中节点连接越紧密。graph density=|E|*2/(|V|*(|V|-1)),这里的E 指的是边数，V 是节点个数，|V|*(|V|-1) 表示最多的连接边数,|E|*2 为实际边数。另外，由于两个算法本质上求出的是k-核图，因此两个算法的graph density 一致。

图1 展示了变化参数λ 时KS-BPS 算法和QS-BPS 算法及预处理过程的运行时间和graph density 两个指标的对比。通过图1 可以看出λ值越大，算法的运行时间越短。这主要是因为当λ的值增大时，需要考虑的节点个数逐渐减少，另外，graph density 值也逐渐减小，这主要是由于当λ 的值增大时，满足条件的节点和边的个数减少。

图2 显示了随着α 逐渐增大，算法的运行时间逐渐增大，这主要是因为当α 的值逐渐增大时，满足持续性的节点逐渐增多。图2也展示了α 的增大对graph density 没有很大的影响。

图3 展示了随着参数γ 的逐渐增大，两个算法的运行时间和graph density 逐渐增大，这主要是因为随着γ 的增大，会有更多的时序边添加到候选子图中。

在图4 中，随着k 值的逐渐增大，QS-BPS 算法的运行时间逐渐增加,这是因为随着k 值的逐渐增大，所检测的图必须包含更大的k-核,需要花费更多的时间。但是KS-BPS 运行时间几乎没有影响，仅稍微降低，这是因为KS-BPS 算法对于不同的k 值都要求先求出节点的核数，所以变化k 值对算法的影响较小。图4 还显示了，随着k 值的逐渐增大，两个算法的graph density 逐渐增大。它的主要原因是k 值设置越大，找到的图越密集。

5 结束语

本文研究了时序图中突发持续子图搜索问题，即搜索出在以最快的速度聚集其密度且持续一段时间的稠密连通子图。首先考虑查询点的邻接点度数和边上权值计算出查询点的重要度，其次由查询点的重要度和突发持续性得到突发持续序列，然后根据查询点的突发持续序列提出了两种不同策略下的突发持续子图搜索算法。最后，通过真实数据集上的实验结果验证了本文提出算法的高效性和有效性。