基于柔性曲轴多体动力学模型的曲轴优化设计
秦利明,钟爱国,李锐,李军
(台州学院,浙江 台州 318000)
随着我国能源经济的发展,节能减排在制冷工程领域越来越受到重视。研究[1-3]表明,制冷用压缩机曲轴系统的重量减轻10%,可降低电耗5%~8%,另外,通过对曲轴结构的优化设计,能够有效减小曲轴系统的质量,减小曲轴运动中产生的惯性力,降低曲轴系统的电耗,同时还可降低曲轴系统的生产成本等。
近年来,很多学者对曲轴系统进行优化,Simon等[4]基于曲轴有限元模型对曲轴系统的疲劳性能进行了优化;Almasi A[5]通过优化往复式压缩机曲轴系统设计和制造过程中的关键部件配置来提高曲轴系统的工作性能和可靠性;李磊等[6]采用多目标优化算法对曲轴系统连杆进行轻量化设计,提高了结构的强度性能和振动性能;黄保科等[7]采用粒子群优化算法对发动机曲轴进行优化,降低了曲轴系统的质量;彭禹等[8]基于有限元单元法和虚拟样机技术对曲轴平衡重进行优化,有效改善了曲轴主轴承载荷工作周期内的平均值。上述研究围绕曲轴系统零部件配置、振动性能、强度性能的优化较多,而对于曲轴平衡重减重孔的分析和优化较少,例如流线型减重孔在曲轴平衡重设计中就很少提及。
基于虚拟试验场仿真技术和试验设计法的神经网络代理模型优化技术,是近年来兴起的一种优化技术,被广泛应用于航空航天、汽车行业、制造行业等领域[9-11]。苗森春等[9]在遗传算法的基础上,采用优化的拉丁超立方试验设计结合CFD技术和神经网络技术对航空用液力透平叶片型线进行优化,提高液力透平效率;武和全等[10]采用遗传算法结合试验设计和有限元分析技术对某车架的前纵梁进行优化,可提高汽车的整车碰撞性能;秦国华等[11]利用遗传算法和神经网络结合多因素正交试验设计对刀具的切削参数进行优化,能减小刀具磨损量。以上研究表明,基于虚拟试验场仿真技术和试验设计法的神经网络代理模型优化技术已在各领域已经取得了较好的应用效果。
本文以某制冷用半封闭往复式压缩机曲轴结构为例,提出了一种流线型平衡重减重孔结构形式,并以曲轴系统质量和扭振特性为优化目标,利用BP神经网络建立流线型减重孔结构参数与扭振性能之间的代理模型,采用非劣排序遗传算法(NSGA-II)对建立的曲轴系统优化模型进行求解。
1 曲轴系统动态建模
1.1 曲轴系统刚柔耦合多体系统模型的建立
参考文献12、13后,本文确定的曲轴系统刚柔耦合多体系统分析流程见图1。
首先,将曲轴CAD模型导入Hypermesh中,定义好相应的单元和材料属性,进行网格划分,曲轴有限元模型如图2所示。曲轴的有限元网格模型全部使用solid185单元划分,对结构突变位置处的网格进行加密,总计45 438个节点和40 392个单元;曲轴结构材料34CrNiMO6,泊松比0.29,密度7.80 g/cm3,弹性模量205GPa;在图2中1~7与Ⅰ、Ⅱ轴段中心位置定义无穷小质量单元,并与对应外接触表面进行刚性耦合,用以各部件的载荷传递。
其次,将采用Hypermesh设置好的求解文件导入ansys中求解,获取模态中性(MNF)文件,再与活塞、连杆等剩余曲轴系统CAD模型一同导入ADAMS软件中,进行零部件组合校验。其中,在Ⅰ、Ⅱ、7处建立曲轴地面之间的转动副,1~6处建立曲轴与连杆大端之间的转动副,连杆小端与活塞之间建立转动副,活塞与地面之间建立移动副。
然后对柔性体边界条件进行设置。曲轴转速为1 500 r/min,施加在7处的转动副。压缩机蒸发压力0.364 MPa,冷凝压力1.838 MPa,气缸作用类型单作用,活塞气体力曲线通过Cubic样条曲线插值获得,施加在相应的活塞上表面中心位置。
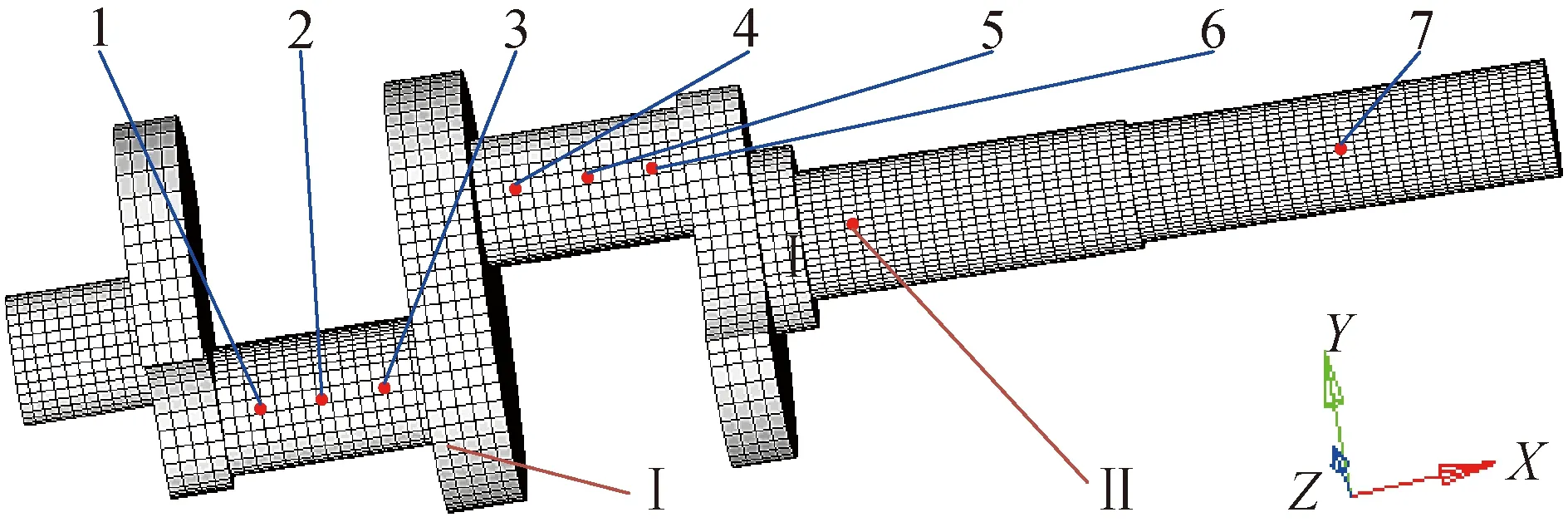
图2 曲轴有限元模型
最后,对所建立的曲轴系统刚柔耦合多体系统模型进行仿真求解。曲轴一个工作周期的时间为0.04 s,为得到稳定的计算结果,共计算4个工作周期,时间为0.16 s,计算步长为0.8×10-4s;再对结果的收敛性进行判定,若收敛,则输出仿真结果,反之,则重新返回到零部件组合校验。
1.2 曲轴动态特性计算结果与分析
曲轴驱动端承受的扭矩最为剧烈,故而扭振性能也最为恶劣,故本文选取曲轴驱动端扭转角位移作为曲轴系统扭振特性的评估指标[14]。质量为11.89 kg曲轴驱动端扭转角位移随时间的变化曲线如图3所示。由图3可知:曲轴驱动端扭转角位移随时间的变化呈现明显的周期性变化,周期为0.04 s,扭转角位移的最高幅值为0.141 6°。

图3 曲轴驱动端扭转角位移随时间变化曲线
1.3 曲轴结构优化参数的确定
为了降低半封闭往复式压缩机曲轴系统的质量和保证曲轴系统的扭振性能,本文提出一种配置流线型减重孔的曲轴系统,然后与原有配置圆形减重孔和未配置减重孔的曲轴系统扭振性能对比。本文提出的减重孔结构形式图4所示,在相同减重质量下配置不同类型减重孔形式的曲轴驱动端扭转角位移随时间的变化关系如图5所示。

图4 平衡重减重孔方案

图5 不同类型减重孔下驱动端扭转角位移对比图
由图5可知:配置不同类型减重孔的曲轴系统驱动端扭转角位移随时间的变化趋势基本一致,且配备流线型减重孔的曲轴系统驱动端扭转角位移峰值最小。这表明:在相同减重质量下配备流线型减重孔的曲轴系统具有最优的扭振性能。因此,为了获得最优的流线型减重孔参数,本文对流线型减重孔的形状参数进行优化,最终确定优化设计模型的变量为:
X=(R3,R4,α),
(1)
式(1)中,R3表示小圆半径,R4表示中心圆半径,α表示两侧小圆中心夹角。
2 曲轴结构优化设计
2.1 基于BP神经网络的NSGA-II算法
在曲轴刚柔耦合多体系统动力学模型中,由于曲轴驱动端扭转角位移是设计参数的隐式函数,没有明确的表达式,故本文曲轴结构优化采用基于BP神经网络的NSGA-II组合优化算法,参考文献15后本文流程图如图6所示,构建的n个输入值、m个输出值的BP神经网络拓扑结构如图7所示。

图6 基于BP神经网络的NSGA-II组合优化流程图
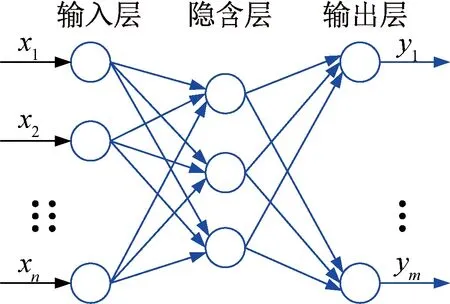
图7 BP神经网络拓扑结构图
为了使得BP神经网络具有联想记忆和预测功能,需要对BP神经网络进行训练,主要步骤如下:
(1)神经网络初始化。根据系统输入输出序列(x,y)确定网络输入层节点数n为3,输出层节点m为1,隐含层节点数l,按照式(2)进行计算后取4,初始化输入层和输出层神经元之间的连接权值wij、wjk,
(2)
(2)隐含层输出计算。隐含层输出H的表达式为
(3)
式(3)中,aj为隐含层阈值,f为隐含层激励函数:
(4)
(3)输出层输出计算。BP神经网络预测输出
(5)
式(4)中bk为输出层阈值。
(4)误差计算。根据BP神经网络预测输出O和期望输出y,计算网络预测误差e,
ek=yk-Ok。
(6)
(5)权值和阈值更新。根据网络预测误差e更新网络连接权值wij、wjk和网络节点阈值a、b,
(7)
wjk=wjk+ηHjek,
(8)
(9)
bk=bk+ek。
(10)
(6)判断算法迭代是否结束,否则返回步骤2。采用Opt-LHD试验设计方法对流线型减重孔形状参数进行设计,将获得的样本点数据转化为模型数据后导入到多体系统模型中,输出仿真结果,如表1所示,然后建立相应的BP神经网络代理模型。
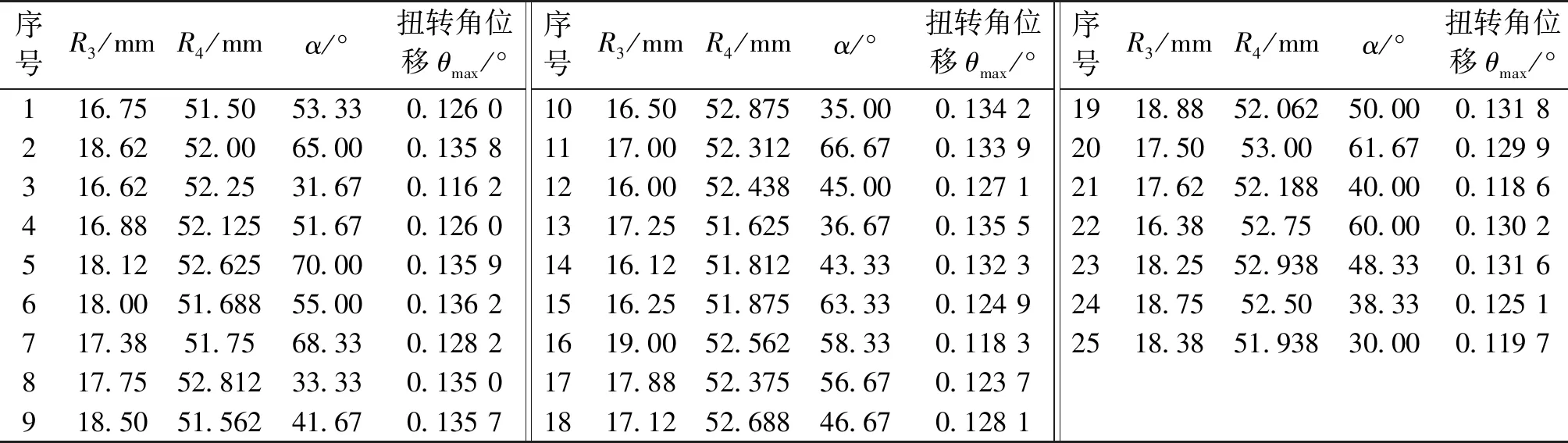
表1 仿真采集的试验数据
为了避免因输入输出数据数量级差别较大而造成网络预测误差较大,采用最大最小法对数据进行归一化处理,函数表达式为
(11)
式(11)中,Yk为原始数据,Ymin为数据序列中的最小数,Ymax为数据序列中的最大数。
将25组数据分为19组,其中3组用以测试,3组用以确证,BP神经网络训练过程如图8所示。
由图8可知:经过2000步计算后,误差达到要求,且扭振角位移真实数据与拟合数据的复相相关系数在0.90以上。这表明可以进行下一步的优化。

图8 BP神经网络训练过程图
2.2 曲轴结构优化设计
以曲轴质量和驱动端扭转角位移最大值为优化目标,以曲轴平衡重流线型减重孔形状参数为优化变量,则制冷用半封闭往复式压缩机曲轴系统的优化数学模型可表示为:
min{m(R3,R4,α),θmax(R3,R4,α)},
(12)
式(12)中,θmax由建立的BP神经网络模型进行预测,m表示曲轴的总质量,其计算公式如下:
(13)
非劣排序遗传算法(NSGA-II)具有并行运算效率高、全局最优解概率大的优势,故采用NSGA-II对上述优化模型进行求解。优化时子代种群规模为100,迭代次数为200,变异概率为0.33,交叉分配指数为30,变异分配指数为100。
Pareto前沿解分布如图9所示。图9显示:曲轴驱动端扭转角位移与曲轴总质量两个目标之间是相互矛盾的,即一个目标的改善需要牺牲另一个目标的性能。这表明设计者应根据实际产品和设计需求,或者凭借经验选择合适的Pareto解。

图9 Pareto前沿解分布图
选取A点作为优化满意解,优化后最终结果如表2所示。
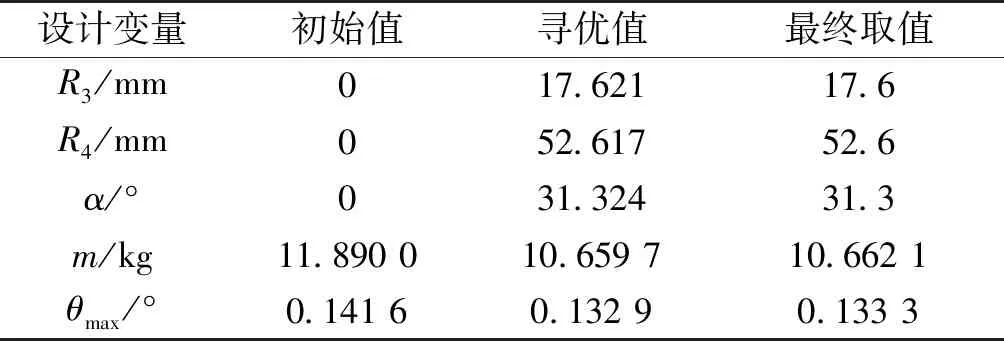
表2 优化前后设计变量和目标函数的对比值
将寻优所得值圆整后代入所建立曲轴系统动力学模型中进行求解,最终取值与优化后所得m和θmax的误差分别为0.023%、0.3%,这表明该优化方法有效。与初始值相比,曲轴总质量降低了10.33%,曲轴驱动端扭转角位移下降了5.86%,表明优化设计能有效改善曲轴系统的质量和扭振性能。
3 结束语
(1)本文提出一种流线型减重孔,与未配置减重孔和配置圆柱形的减重孔进行曲轴系统扭振性能的对比结果表明:在相同减重质量下,配置流线型减重孔的曲轴系统具有最优的扭振性能。
(2)基于刚柔耦合多体系统动力学模型,结合试验设计和BP神经网络代理模型技术,建立了曲轴驱动端扭转角位移与流线型减重孔形状参数之间的神经网络模型,并采用NSGA-II对建立的曲轴系统优化模型进行求解,减少了曲轴优化设计计算的工作量。
(3)利用本文提出的组合优化方法可有效降低曲轴的质量,改善曲轴的扭振性能,这可为改善整机的振动、噪声性能的设计参数提供依据,另外,设计者可按需求选择满意的优化结果,从而缩短产品的研发周期和降低产品的研发成本。

