城市轨道交通列车轮对磨耗模型研究

吴 健，叶正君，邢宗义

（1. 中车青岛四方机车车辆股份有限公司，青岛 266111；2. 南京理工大学 自动化学院，南京 210094）

随着城市轨道交通的迅猛发展，其系统也面临着诸多问题[1]。以地铁列车系统为例，轮对作为列车车体重要组成部件之一，在列车运行过程中起着引导列车车体沿着钢轨正确前进与转弯的作用，此外还要承受来自轨道和列车车体的全部动、静载荷，以上种种因素造成的严峻工作环境使得轮对失效问题已然成为地铁系统最常碰到的问题[2]。实时掌握轮对状况，保障轮对正常的服役性能，对保证地铁列车正常安全运营具有重要意义。

常见的轮对失效形式为轮对的磨耗损伤[3]。自轮对开始服役时刻起，磨耗伴随其整个服役周期直至报废退役。对轮对磨耗模型进行研究，准确掌握轮对型面变化，有助于保障轮对系统的安全性与可靠性，已成为轮对维保的关注重点[4]。当前，针对轮对磨耗模型的研究可分成两种方式：（1）基于动力学仿真分析；（2）基于磨耗数据统计分析[5]。如Jendel基于GENSYS软件平台建立列车动力学模型，结合FASTSIM算法和Archard磨耗模型，实现轮对磨耗趋势的预测[6]。Wei Zhu利用多项式模型去拟合大量现场轮缘厚磨耗历史数据，采用非线性最小二乘法的卡尔曼滤波方法对磨耗模型进行修正，最终得到精度良好的轮缘厚磨耗模型[7]。考虑到现场轮对磨耗历史数据存在主观性强、数据条目缺失等问题，将影响到轮对磨耗模型的准确性，本文基于SIMPACK软件建立某地铁线网下的机车及轨道多体动力学模型，结合接触斑分析算法与Archard磨耗模型，实现轮对型面磨耗的分析；采用轮对磨耗仿真流程，实现轮对磨耗模型的建立。

1 轮对磨耗模型

轮对磨耗模型包含机车/轨道多体动力学模型、轮轨接触斑分析及轮对磨耗仿真流程。通过机车及轨道多体动力学模型，模拟列车运行过程中的轮轨接触作用，输出接触斑位置、法向接触力等在内的轮轨接触斑变量。在获得接触斑变量基础上，结合接触斑分析算法，实现接触斑内黏滑区界定。针对滑动区，采用Archard磨耗模型，计算得到轮轨接触斑内垂直磨耗分布情况。将轮轨接触斑磨耗分布累加并反映到轮对型面，实现轮对型面磨耗分布的计算。在此基础上，以型面最大磨耗深度0.05 m为间隔，对轮对型面进行更新，更新后进行新一轮的轮对磨耗仿真，过程如图1所示。

1.1 机车/轨道多体动力学模型

为实现对实际轮轨接触作用的仿真，需要建立机车/轨道多体动力学模型，确定对轮轨接触关系影响显著的轮/轨基本参数，忽略影响甚微的参数[8]。根据现场实际的轮对情况，轮对初始型面采用实测的S10002型型面，车轮名义直径设定为840 mm，轮缘内侧距设定为1353 mm。考虑到轮对上细微的弹性变形都会直接影响到轮轨接触关系，将轮对设为弹性体。其他轮对基本物理参数，如表1所示。

继续对机车整车进行建模，机车动力学模型主要由1个机车车体、2个转向架、4个轮对及8个轴箱装置等部分构成，如图2所示，机车的主要参数如表2所示。

表1 轮对基本参数

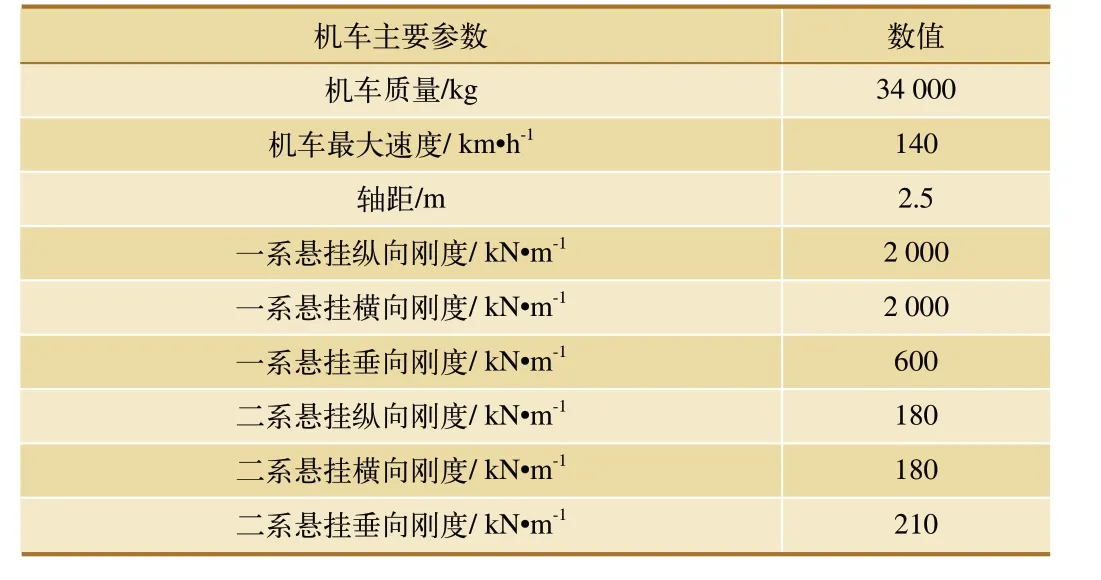
表2 机车基本参数

结合现场实际轨道情况，轨道初始型面采用实测UIC60型型面，轨底坡设为1：40，轨距设为1435 mm，轮轨摩擦系数设为0.4。与轮对建模类似，将轨道设为弹性体，即会发生弹性变形。由于不同曲线半径的轨道线形将产生不同的轮轨接触关系，故需根据实际线路情况建立轨道线路模型，其中，线路总长约为14.4 km，轨道不同区段具有不同的曲线半径，同时，每个区段具有指定的超高值，线路具体的几何条件如表3所示。

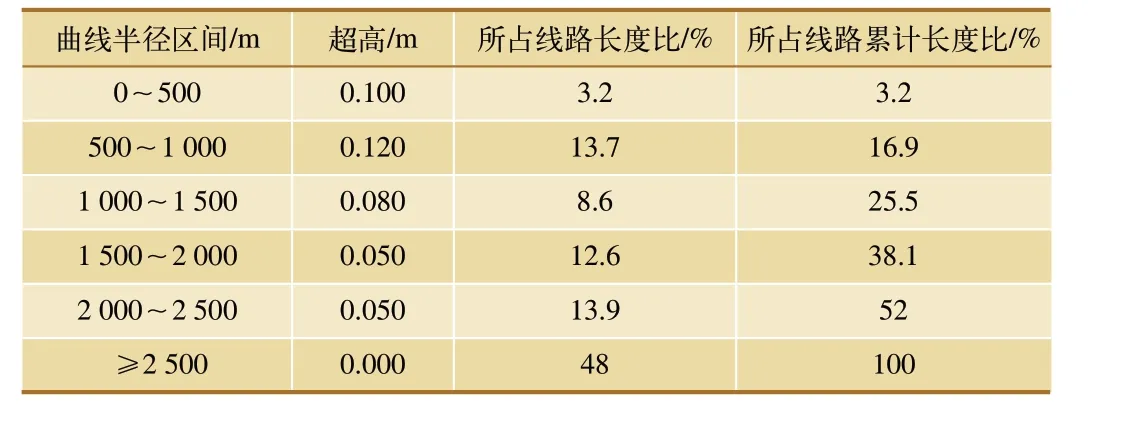
表3 轨道线路几何条件

建立机车及轨道多体动力学模型后，通过SIMPACK软件模拟轮对沿轨道运行情况，分析计算并输出轮对磨耗情况的相关轮轨接触变量，相关变量如表4所示。

表4 轮轨接触变量

1.2 轮轨接触斑黏滑区界定

轮轨接触斑黏滑区界定一直是接触斑分析的重点，它能判断接触斑内会产生磨耗效应的区域，为分析接触斑内磨耗分布情况奠定基础，而接触斑黏滑区问题主要涉及轮轨接触斑切向接触问题。目前，Kalker线性简化理论在处理轮轨接触斑切向接触问题上得到了大量应用[9]。

将动力学模型输出的椭圆形轮轨接触斑作为研究对象进行接触斑黏滑区分析，其中，接触斑内法向力分布情况为：

式中，N为接触斑内法向合力，a、b为椭圆半轴长，x、y为基于轮轨坐标系接触斑内的坐标点。

Kalker线性简化理论假设接触斑中任意点(x,y)的位移ui只与该点的力pi有关[10]，i可取x、y，分别表示在轮轨接触坐标系下的纵向、横向方向。以轮轨接触斑为例，u与p的关系可表示为：

式中，u(x,y)为轮对型面上接触斑某点的弹性位移矩阵，p(x,y)为对应点的作用力矩阵，Li为对应方向的轮对材料柔度系数。

令a(y)表示椭圆接触斑边缘，通过Kalker线性简化理论计算接触斑切向力为：

式中，C11、C22、C23为Kalker系数，G为轮轨材料合成剪切模量。

基于u与p的关系，结合Kalker线性简化理论得到稳态接触状态下的滑动方程表达式为[11]：

式中，vx、vy分别为纵向、横向滑动速度，vv为机车运行速度，η、ε、φ分别为纵向、横向、自旋蠕滑率，px、py分别为接触点处纵向、横向作用力。

为了方便计算，对式（4）进行无量纲化操作，

或表示为矩阵矢量形式：

式中，w=(wx wy)为总滑动矢量，s=(nx-y'φxny+x'φy)为刚性滑动矢量，为弹性滑动矢量。

通过以上无量纲化操作，将Hertz接触理论的椭圆形接触斑转换为单位圆接触斑。取单位圆上任意一条平行于x'轴、宽为dy'的带，从带上的一点x1'=x0'-h到x0'作积分，当h取足够小，式（6）可转化为：

h取带长的1/10，从带右边界开始，在边界上的力理想化为0，故p'(x0')=(00)，向后按照依次对整条带的刚性滑动矢量进行求解。值得注意的是，通过上述积分方法，w|xo'-h/2具体值仍无法求解，针对这一问题引入库伦摩擦定律，即单位圆接触斑内任意一点都满足以下情况：

定义z'=p/z0，pH=p0'-s|xo'-h/2。

（1）如果|pH|≤fz'，则该点为黏着状态，p1'=pH且w|xo'-h/2=(00)；

（2）如果|pH|＞fz'，则该点为滑动状态，p1'=(fz'/|pH|)pH且w|xo'-h/2=-λp1'，其中，λ=|pH|/(fz')-1且λ＞0；

基于式（7）并结合上述分析，可实现判断单位圆接触班内10×10个离散点的黏滑状况，此外，还能计算出每个离散点的总滑动矢量w。

1.3 轮轨接触斑磨耗分布分析

在实现轮轨接触斑黏滑区界定后，采用Archard磨耗模型进一步分析接触斑内的磨耗情况。

Archard磨耗模型定义接触斑内滑动点的磨耗深度为[12]：

式中，Δz为滑动点的磨耗深度，pz为滑动点的法向力（单位：N），Δd表示单位Δt内的滑动距离，在此Δt时间内，轮对型面接触斑内的任意点一直处于接触斑内的一个滑动点范围中，H为材料硬度（单位：N/m2），kw为无量纲的磨耗系数，该系数的具体取值与法向力、滑动速度有关[13]。可参考文献[14]中的kw表确定具体取值。

其中，滑动距离Δd可表示为：

式中，vx、vy为滑动速度（由接触斑分析算法计算得到），vc为滑动点通过接触斑的速度，Δx为运行方向上滑动点的长度。

在此基础上，理想化地假定弹性速度相比于刚性速度可忽略不计，结合式（1），可得到Archard磨耗模型的最终表达式为：

1.4 轮对磨耗仿真流程

在1.1～1.3节的研究基础上，针对轮对型面磨耗仿真的流程如下：

（1）基于轮轨接触关系动力学模型分析并输出当前采样点下的轮轨接触变量；

（2）将轮轨接触变量通过接触斑磨耗模型计算出各接触斑内磨耗深度分布；

（3）结合轮对型面上接触斑起始位置yws、终止位置ywe，确定各接触斑在轮对型面上的位置；

（4）沿轮对型面坐标点取在轮对型面坐标系x轴方向上的磨耗深度最大值作为对应型面坐标点的磨耗深度；

（5）循环若干次（1）～（4），计算多个采样点下的轮对型面磨耗情况，不断累加轮对型面各坐标点的磨耗深度，直到型面上某坐标点的最大磨耗深度达到0.05 mm时，更新原轮对型面并进行新一轮的轮对磨耗仿真。

2 模型结果及验证

2.1 轮对磨耗仿真分析

以前转向架前轮对的左车轮为研究对象，通过SIMPACK软件分析计算，可得到机车运行过程中某采样点下的轮轨接触变量，如表5所示。

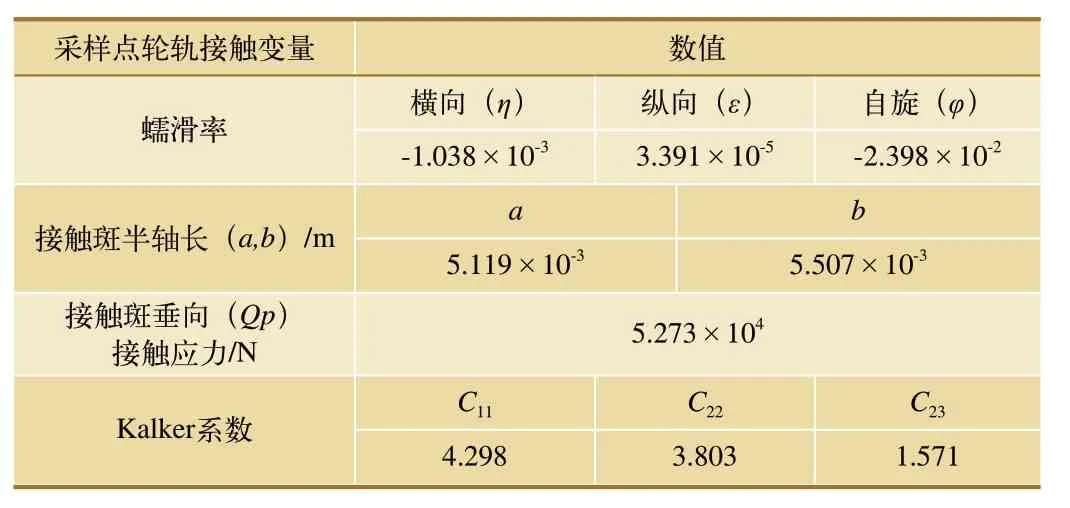
表5 某采样点轮轨接触变量

以表5所示的轮轨接触变量为例对轮轨接触斑进行分析，得到对应采样点下单位圆接触斑的总滑动矢量w分布，如表6所示。

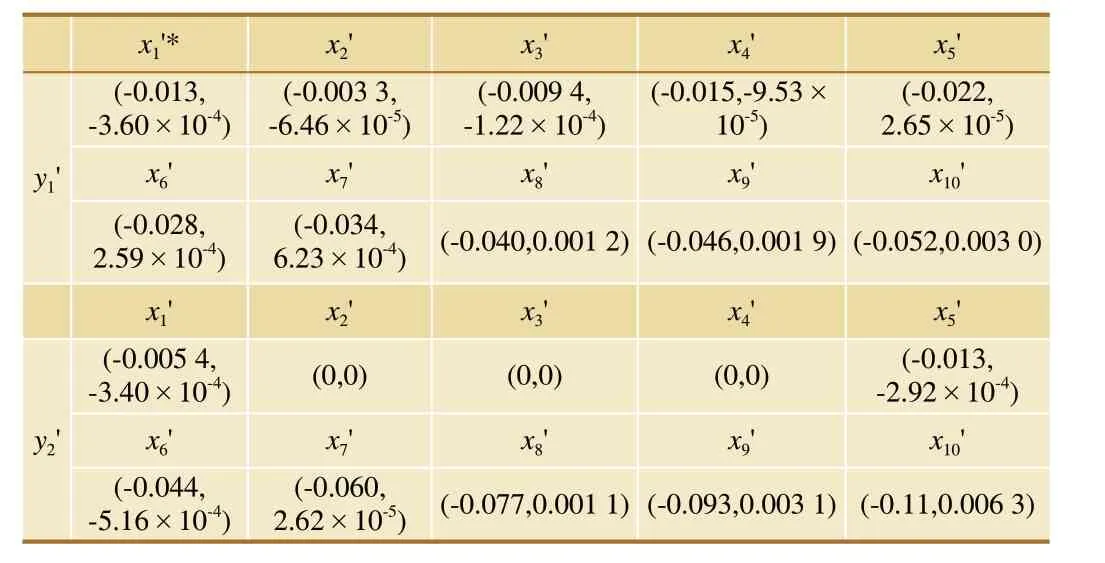
表6 单位圆接触斑内总滑动矢量分布（部分）

在实现轮轨接触斑黏滑区界定基础上，基于Archard磨耗模型计算车轮滚动一周后轮轨接触斑内每个滑动点的垂直磨耗量，以获得整个接触斑的垂直磨耗分布，如图3所示。

结合轮对磨耗仿真流程模拟轮对型面磨耗情况，以0.25 mm型面最大磨耗深度为间隔观察轮对型面磨耗发展趋势，结果如图4所示。

值得注意的是，图4所示的轮对型面磨耗分布曲线经快速傅里叶变换低通滤波平滑处理，滤除曲线锯齿噪声使结果更接近实际磨耗情况[15]。

2.2 轮对磨耗验证

以模型输出的运行10000 km的轮对磨耗型面为验证对象，将其与同线路下运行相同里程的实测磨耗型面进行比较，以验证模型的准确性。轮对型面的测量借助于车辆段现场架设的轮对尺寸检测系统，系统可动态检测出轮对型面形状，且检测效果已得到验证，现场检测系统如图5所示。

从图6所示的轮对型面对比图可看出，实测轮对型面的磨耗范围较仿真型面更大，且型面磨耗更加平滑。此外，实测轮对型面与仿真轮对型面在踏面部分最大磨耗深度差约为0.0728 mm，实测型面相较于仿真型面磨耗程度更加严重。从总体上看，实测型面与仿真型面曲线无论是磨耗范围还是磨耗深度都较为一致，在一定程度上验证了轮对磨耗模型的准确性。

3 结束语

本文提出的轮对磨耗模型能对轮对运行过程中型面磨耗情况进行仿真模拟并预测，模型结果得到了验证。由于轮对型面的改变会对轮轨接触关系产生影响，而受磨耗影响，轮对型面也时刻发生着变化。考虑到本文更新轮对型面是离散的，会对磨耗仿真结果造成一定的误差。在下一阶段，可通过编写SIMPACK接口程序，对每个采样点计算型面磨耗分布后自动完成对轮对型面的更新，以提升模型精度。