一种基于服务质量的多UAV容量优化方法
邹昳琨,王 钢,周若飞
(哈尔滨工业大学 电子与信息工程学院,黑龙江 哈尔滨 150080)
0 引言
近些年来,无人机飞行器的研发以及应用已经引起了全球各国政府的高度关注和重视,无人机飞行器进入了一个高速发展阶段。无人机(Unmanned Aerial Vehicle,UAV)系统可以为偏远地区提供无线网络覆盖,也可以作为地面通信网络与卫星通信网络之间信息传递的有效中继[1,2]。UAV 具有体积小、灵活性强、可快速部署等优点,可广泛用于各个领域[3-6]。与单一UAV系统相比,使用多UAV系统来执行任务的效率更高,具体来说,在执行任务所需时间,执行任务区域范围甚至任务有效负载均衡等方面获得更多的益处[7-8]。
迄今为止,对3D空间中的自主UAV之间的通信性能进行的研究很少。大多数现有研究都是基于UAV的静态设置,或简化、确定性的UAV姿态或者飞行轨迹[9-10]。例如,ABSOLUTE项目采用静态或半静态UAV作为高级长期演进(Long Term Evolution-Advanced,LTE-A)系统空中基站(Base Stations,BSs),在大规模自然灾害期间和之后提供无线覆盖。UAV作为无人运行的空中BSs,同时也可以作为异构网络架构的一部分来实现公共安全通信[11-12]。同时,大量研究都集中在分析2D空间中移动或静止发射机和接收机之间链路的遍历容量、中断概率和中断容量[13-14]。对于UAV网络的容量优化研究一直处于相对空白的状态,而UAV网络作为未来6G通信发展的重要趋势[15],已成为一种不可忽视的重要技术。因此,本文将对多UAV系统的网络容量进行分析和优化。
针对多UAV系统中不同用户的服务质量(Quality of Service,QoS)差异的特性,提出一种联合用户调度、发射功率和飞行轨迹的网络容量优化算法。
1 网络模型与问题制定


图1 多UAV无线网络Fig.1 Multi-UAV wireless network
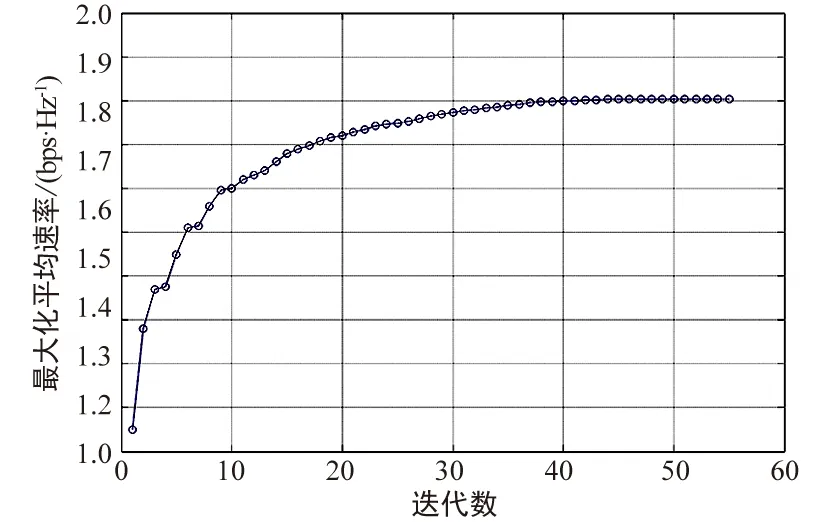
本文采用3D笛卡尔坐标系,其中每个地面用户k的水平坐标为wk=[xk,yk,zk]T∈3×1,其中在固定时间t(0 (1) 假设从UAV到地面用户的通信链路由视距链路(Line of Sight,LoS)支配,其中信道质量仅取决于UAV用户距离。此外,假设UAV移动性引起的多普勒效应在接收器处得到很好的补偿。因此,在时隙n期间从UAVm到用户k的信道功率增益遵循自由空间路径损耗模型,可表示为: (2) 式中,ρ0表示参考距离d0=1 m处的信道功率。定义二进制变量αk,m[n],表示如果αk,m[n]=1则用户k由UAVm在时隙n中服务;否则,αk,m[n]=0。定义范围在[0,1]之间的变量βm为服务质量的权重系数。用户k处的相应接收信号与干扰加噪声比(SINR)可表示为: (3) 式中,σ2为接收器处加性高斯白噪声(AWGN)的功率。因此,Rk[n]为用户k在时隙n中可实现的速率(bit·s-1·Hz-1),可表示为: (4) (5a) (5b) (5c) (5d) αk,m[n]∈{0,1},∀k,m,n (5e) (5f) qm(1)=qm(N) (5g) (5h) 0≤pm[n]≤Pmax, ∀m,n (5i) 为了使式(5)更容易处理,首先将(5e)中的二元变量放宽为连续变量,这会产生以下问题: (6a) s.t.0≤αk,m[n]≤1,∀k,m,n (6b) (5b),(5c),(5d),(5f),(5g),(5h),(5i) (6c) 尽管松弛,但由于非凸约束公式(5b),式(6)仍然是非凸优化问题。通常没有标准方法有效地解决这种非凸优化问题。在下文中,将通过应用块坐标下降和连续凸优化技术,为松弛式(6)提出了一种有效的迭代算法。 对于任何给定的UAV轨迹和发射功率{Q,P},可以通过解决以下问题来优化式(6)用户调度和关联: (7a) (7b) (7c) (7d) 0≤αk,m[n]≤1,∀k,m,n (7e) 由于式(7)是标准LP,因此可以通过诸如CVX的现有优化工具有效地解决它。 (8a) (8b) (8c) (8d) qm(1)=qm(N),∀m (8e) (8f) 式(8)是凸优化问题,可以通过标准凸优化求解器如CVX 有效地求解。 (9a) (9b) 0≤pm[n]≤Pmax,∀m,n (9c) 问题(9)是凸优化问题,可以通过标准凸优化求解器(如CVX )有效地求解。然后应用块坐标下降法,得到最终的容量优化算法1。 算法1 问题(6)的块坐标下降算法1:初始化 Q0 和 P0,使得 r = 0。2:repeat3: 给定{Qr,Pr}解出问题 (7)的最优解{Ar+1}4: 给定{Ar+1,Qr,Pr}解出问题 (8)的最优解{Qr+1}5: {Ar+1,Qr+1,Pr}解出问题 (9)的最优解{Pr+1}6: 更新 r= r+17:until 目标值的差值小于阈值ε>0 below a threshold ε>0 本文考虑具有K=6个地面用户的系统,其在2×2 km2的2D区域内随机且均匀分布。所有UAV假设飞行的固定高度为H=90 m。假设接收机噪声功率为σ2=-110 dBm。参考距离d0=1 m处的信道功率增益设置为ρ0=-60 dB。UAV的最大发射功率和最大速度分别假设为Pmax=0.5 W和Vmax=50 m/s。算法1中的阈值ε设置为10-4。UAV的发射功率由最大发射功率初始化,即pm[n]=Pmax,∀m。其他参数设置为dmin=100 m 和τ=100,服务质量权重从β1~β6依次为0.15,0.05,0.35,0.10,0.15,0.20。 在性能比较之前,展示了T=70 s时两个UAV的情况,如图2所示。图3为提出的算法1的收敛行为,从图中可以看出,所提出的算法实现的最大平均速率随着迭代次数的增加而快速增加,并且算法在大约40次迭代后收敛。 图4比较了算法1和未考虑QoS的优化算法的最大化平均功率。从图中可以看出在0~70 s间所提算法的数值和增幅均超过未考虑QoS的优化算法,这是因为用户3的服务质量权重明显大于用户1和用户2。所以UAV的轨迹将更加靠近用户,以此为用户3提供更高的传输速率,从而提高整个网络的最大化平均速率。但是在70 s以后由于UAV向低需求的用户靠近,所以平均速率的增幅开始下降。但是由于算法倾向于高需求用户,因此网络最大化平均速率还是高于未考虑QoS的优化算法。 图2 UAV轨迹优化Fig.2 UAV trace optimization 图3 本文算法1的收敛性表现Fig.3 Convergence performance of Algorithm 1 in this paper 图4 双UAV系统中算法1与未考虑QoS算法的比较Fig.4 Comparison of algorithm 1 and QoS-independent algorithms in dual UAV systems 本文提出了一种基于用户质量的多UAV容量优化算法,在将服务质量设置为权重参数的基础上,利用连续凸优化技术和块坐标下降算法,解决了多UAV通信系统中的容量优化问题。仿真结果证明了该算法的收敛性,同时表明了在相同条件下基于用户质量的多UAV容量算法能够使系统达到更高的平均传输速率,从而说明了该算法的有效性。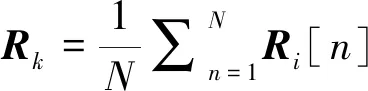
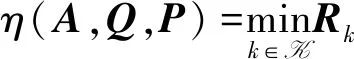
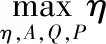
2 网络容量优化方案
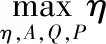
2.1 用户调度和关联优化
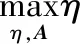
2.2 UAV轨迹优化
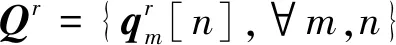



2.3 UAV发射功率控制

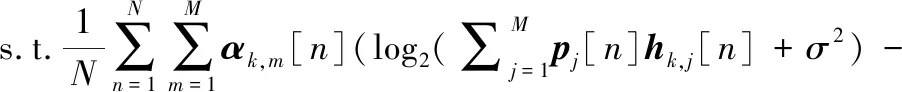

3 仿真分析


4 结束语

