“由形识数”：你会画长度为无理数的线段吗

杨晓彬

我们都知道，实数与数轴上的点一一对应，借助数轴，我们可以很轻易地画出长度为有理数的线段。那么，你会画长度为无理数的线段吗？

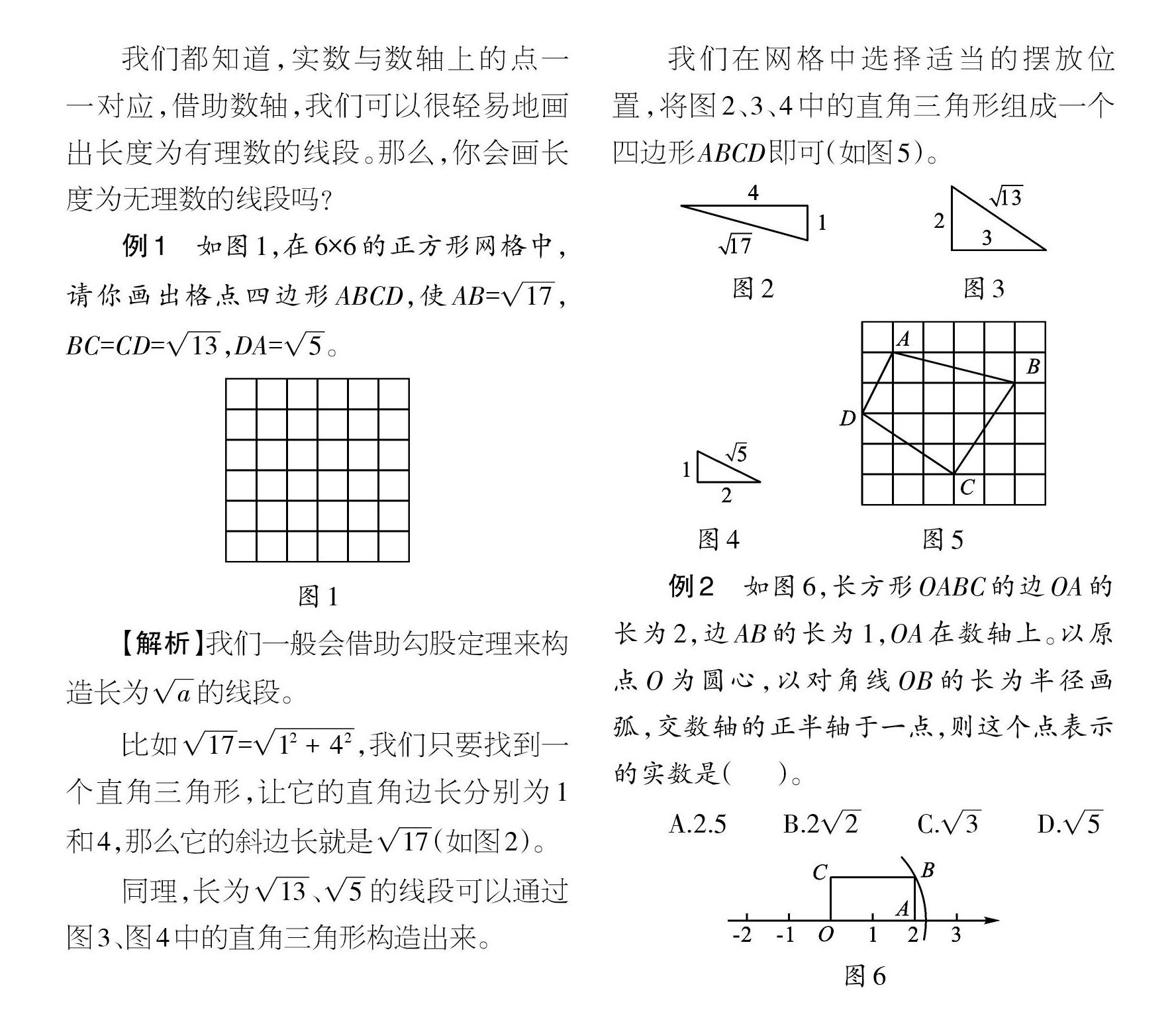
例1 如图1，在6x6的正方形网格中，请你画出格点四边形ABCD，使AB=√17，BC=CD=√13，DA=√5。

【解析】我们一般会借助勾股定理来构造长为√a的线段。

比如√17=√1²+4²，我们只要找到一个直角三角形，让它的直角边长分别为1和4，那么它的斜边长就是√17（如图2）。

同理，长为√13、√5的线段可以通过图3、图4中的直角三角形构造出来。

我们在网格中选择适当的摆放位置，将图2、3、4中的直角三角形组成一个四边形ABCD即可（如图5）。

例2如图6，长方形OABC的边OA的长为2，边AB的长为1，OA在数轴上。以原点O为圆心，以对角线OB的长为半径画弧，交数轴的正半轴于一点，则这个点表示的实数是（ ）。

A.2.5 B.2√2 C.√3 D.√5

【解析】要确定数轴上一个点表示的实数，只要知道这个点到原点的距离是多少，再根据这个点位于正半轴还是负半轴，确定实数的符号即可。

因为在长方形OABC中，∠BA0=90°，所以我们连接OB，在直角三角形OAB中，由勾股定理，可得对角线OB=√5，即要求的实数到原点的距离是√5。又因为这个数在正半轴，所以选D。

例3如图7，数轴上表示1、√3的点分别为点A、B，点B关于点A的对称点为点B'，则点B表示的实数为____。

【解析】要確定点B'表示的数，首先要确定线段OB的长。

因为已知条件告诉我们，点A、B表示的数分别是1、√3，所以OA=1，OB=√3，所以AB=OB-OA=√3-1。因为点B、B'关于点A对称，所以AB'=AB=√3-1。又因为OB'=OA-AB'，所以OB'=1-（√3-1）=2一√3。有的同学做到这里就结束了，其实不然，我们还要判断该实数的符号。因为点B在正半轴，所以它表示的实数为2一√3。

小试牛刀

1.请在数轴上找到一√8对应的点。

2.已知⊙A的半径为1，将其按如图9所示方式置于数轴上，使圆周上点P与数轴原点重合。若将⊙A沿数轴正方向滚动一周，点P落在数轴上的点P'处.则点P'对应的实数是____。

3.已知点O为数轴的原点，点A、B在数轴上，若AO=3，AB=√17，且点A表示的数比点B表示的数小，则点B表示的数是____。

参考答案：1.如图10所示。

第2、3题的答案请扫描下方二维码查看。

（作者单位：江苏省连云港市海州实验中学）