基于格子玻尔兹曼方法的液滴撞击液膜数值模拟
鲁舟洋,邢 岩
(1.中国电建集团西北勘测设计研究院有限公司,陕西 西安 710065;2.交通运输部天津水运工程科学研究所工程泥沙交通运输行业重点实验室,天津 300456)
0 引言
液滴撞击液膜现象广泛存在于自然现象和工业制造中,该现象发生往往伴随着复杂的传热传质过程。一系列研究表明,液滴撞击液膜过程中液冠演化过程受到众多参数的影响,这些参数通常包括雷诺数(Re),韦伯数(We),气液密度比,气液粘滞系数比,液膜高度等。Rioboo[1]等通过实验研究了液滴半径对液冠演化的影响,并将该过程分为六个阶段。Rein[2]、Yarin[3]等系列研究表明,液体飞溅过程中,会发生液滴从液冠脱落,即液滴飞溅现象。随后Wang 等[4]研究了不同Re 数、We 数及液面厚度对液冠演化的影响。
随着计算机技术的发展,计算流体力学研究结果可以有效展示复杂流场的演化过程,逐渐成为研究流体运动的重要手段。格子玻尔兹曼方法(LBM)作为介观数值模拟方法,能够有效模拟气液交界面变化复杂的流动现象。经过近30 a 的发展,现有LBM多相流模型可以归纳为伪势模型、颜色模型、自由能模型和相场模型[5]。Lee[6]等人首先利用相场模型模拟、不同Re条件下,液滴撞击液膜的过程。Wang[7]等则利用基于有限体积法的LBM自由能模型模拟Re 从20~1000 条件下液滴飞溅的过程。黄虎[8]等则利用LBM相场模型模拟We=500 和Re=24~480条件下的液滴撞击液膜的过程。以上研究均表明:不同LBM可以有效模拟液滴撞击液面的过程。
总结前人研究发现,基于LBM 的数值模拟研究中,尚未利用伪势LBM 模型对气液密度比超过500 的液滴撞击液膜现象进行模拟。因此本文利用大密度比LBM 伪势模型,结合可调节表面张力的外力模型,模拟两相密度比为ρL/ρg,不同Re 数和We 数下液冠演化过程,分析这些参数对液冠半径和液冠高度的影响,并进一步研究液膜厚度对液滴飞溅过程的影响。
1 大密度比伪势LBM 方法
本文采用的多松弛碰撞算子LBM伪势模型,对应粒子分布方程为:

式中:ε 用于调节热力学一致性。其中ρ 为宏观密度,ux,uy为宏观速度。
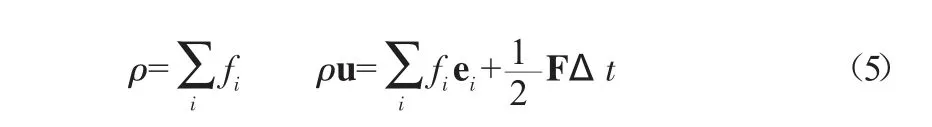
其中式(5)为对应宏观量求解方式。F 为作用于流体上作用力,包括粒子间作用力Fm等,其中粒子间作用力:

pEOS为通过流体状态方程求得压强。本文采用Carnahan-Starling(C-S)状态方程:
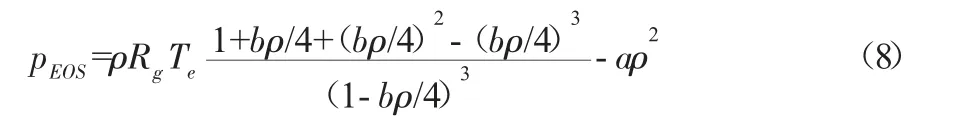
式中:a=0.4963R2Tc2/pc,b=0.1873RTc/pc,其中Tc,pc分别为该气体的临界温度与临界压强。本研究中状态方程中相关参数为a=1,b=4,Rg=1。同时本文引入Li提出表面张力调节项,可以在伪势模型中不通过调节密度比达到调节表面张力的目的:
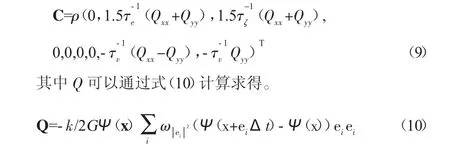
式中:k 为调节表面张力系数,取值在0~1 之间。
2 模拟结果与分析
由于液滴撞击液膜受到液滴撞击速度,液相粘滞系数,液体表面张力等多种因素的影响,为更系统的研究概述这些因素的影响,本研究依旧沿袭前人的分析方法,引入多个无量纲参数分析液面的演化过程。引入无量纲参数包括雷诺数(Re)、韦伯数(We)、以及相对厚度和无量纲时间。

式中:vL为液体粘滞系数,U 为液滴撞击速度。

式中:σ 为表面张力。
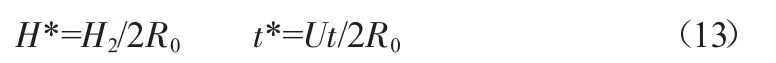
式中:H2为液膜厚度。
2.1 初始条件
为验证模型的准确性,本文采用1001×351 矩形计算域,计算域底部固壁采用标准反弹边界,左右均采用周期边界,而计算域顶部采用非平衡外推边界,计算区域见图1。其中液滴初始半径为R0,液滴初始垂向速度为U,液滴中心距液膜高度为H1,液膜高度为H2,计算中各工况选取参数见表1。
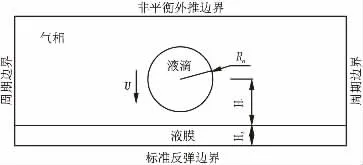
图1 液滴撞击液面计算域示意图
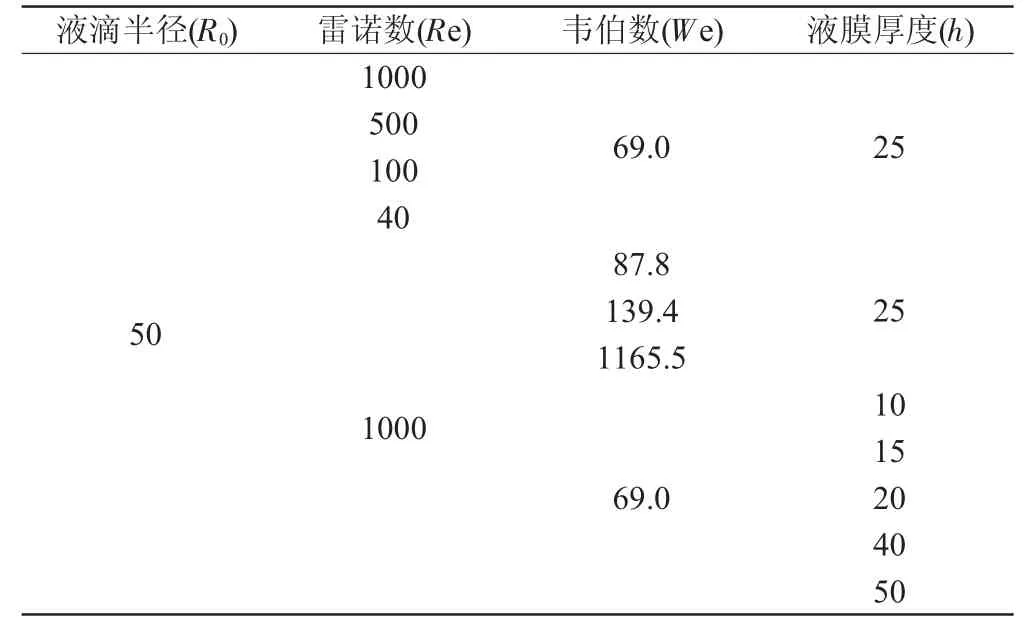
表1 液滴撞击液面计算工况
本研究中液滴撞击速度设为U=0.125,通过调节松弛系数τv和k 来获得不同的Re 数和We 数。为保证热力学一致性,式(4)中ε 取值为0.11。同时为保证计算时数值计算稳定性,减小初始界面附近密度梯度,液滴周围密度场初始化见式(14)。
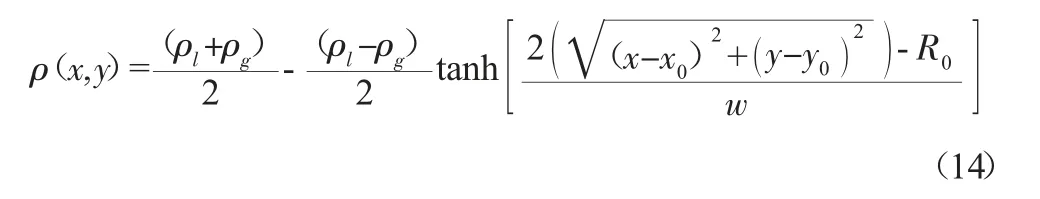
其中(x0,y0)为液滴中心,初始界面厚度w=5。而液膜附近密度初始化公式为:
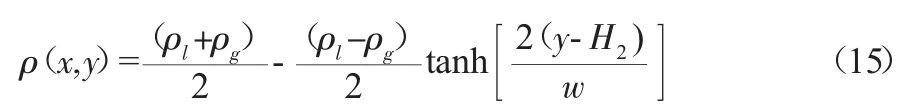
2.2 不同Re 对液面演化的影响
本研究在保证撞击速度不变的前提下,通过改变液体粘滞系数,获得四组不同的Re 数,分别为Re=40、200、500、1000,用来观察不同Re 数对液冠形态的影响。图2 展示了不同Re 对液冠形态的变化的影响,图中可以看到Re=40 时,并未形成有效液冠,但其他三个工况形成液冠均非常明显。从图中可以看到当t*=1.5 时刻,不同Re 条件下数液冠均未发生液滴飞溅现象。但当t*=2.5 时,而当Re 数增大到1000 后,液体尖端受到Rayleigh-Plateau 不稳定性的影响,从而发生液滴飞溅。
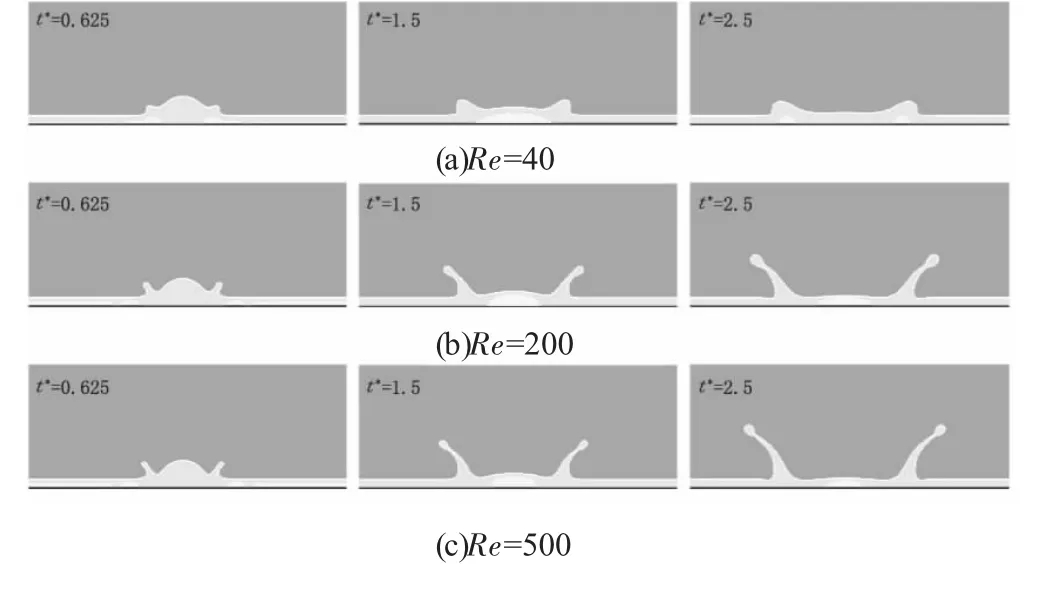
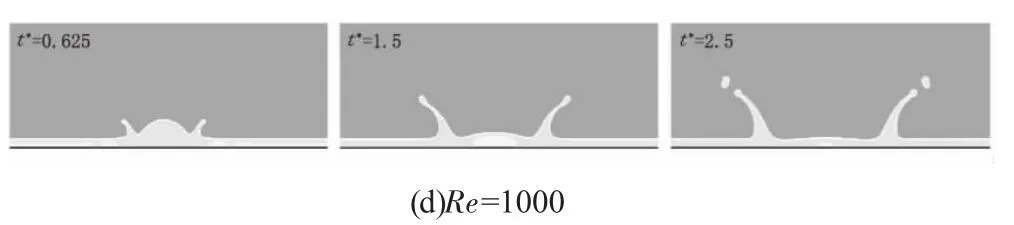
图2 不同Re 条件下液冠形态演化过程
图3 展示了不同Re 条件下,无量纲液冠半径与无量纲时间之间的关系。从图中可以看出,不同Re 数条件下r/2R0和均成正比关系,与理论分析一致。同时斜率k 随着Re 数的增大而增大。同时在图上我们可以看出,当Re=40 时斜率与Re=200、500、1000 三个工况斜率相差较大,这是由于Re=40 时受到液体粘滞系数的影响,并未形成有效液冠。
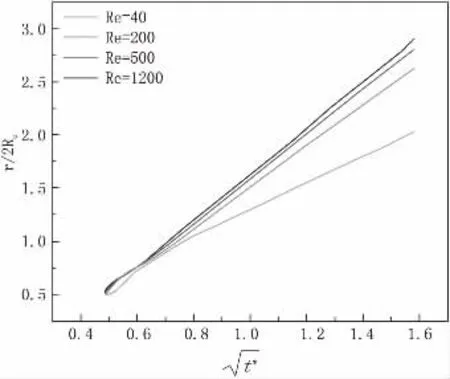
图3 不同Re 数液冠半径r/2R0 与无量纲时间之间关系
2.3 不同We 对液面演化的影响
液滴撞击液膜过程中,液冠飞溅效应会随着We 数增大而变强。图4 展示了Re=500,H*=2.5 条件下不同We 数条件下,液冠在t*=0.625 和t*=2.5 时流场形态。当t*=0.625 时,不同We条件下,液滴两侧均形成液冠水柱,可以看到液冠水柱厚度随着We 的增大而减小。而当t*=2.5 时,We=87.8、139.4、1165.5 三种条件下均能观测到液滴飞溅的过程,但飞溅液滴大小随着We 的增大而显著减小,液冠厚度也减小。原因在于表面张力减小,导致液柱受到Rayleigh-Plateau 不稳定性更强,液冠难以维持稳定形态,末端液滴更容易发生脱落。
图4 不同We 条件下液冠形态变化
图5 展示了不同We 条件下,无量纲液冠半径与无量纲时间之间的关系。本研究表明,在We=69.0、87.8、139.4 三种工况下,液冠半径r/2R0和均成正比关系,与理论分析一致,但当We 增加到1165.5 时,液冠半径与无量纲时间并不成线性关系,这是由于液冠末端液滴脱落过早,液滴不受液冠影响而导致的。图中可以得到在We 由69.0 增加到139.4 过程中对斜率k 值影响并不大。
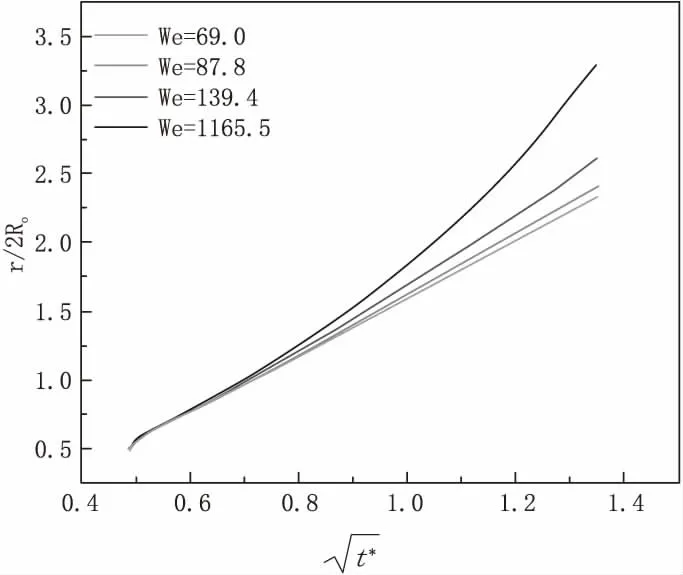
图5 不同We 数液冠半径r/2R0 与无量纲时间之间关系
2.4 液膜厚度对液滴飞溅影响
液膜厚度对液冠形状的演化具有重要意义,Wang 实验研究表明[4],随着液膜厚度减小,液滴撞击液膜过程中更容易发生散裂。图6 展示了Re=500 时六种不同液膜高度条件下,t*=1.875 时液冠形状。液冠演化过程中,液冠液柱与液膜之间的夹角随着液膜厚度的增加而增大,这与Wang 实验一致。
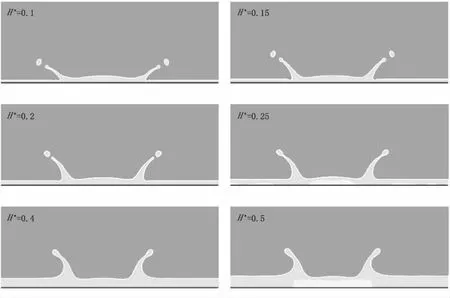
图6 不同H*条件下液冠形态变化
不同H*条件下,液冠半径与无量纲时间之间的关系见图7。本研究表明,在不同液膜厚度条件下,液冠半径r/2R0和均成正比关系,与理论分析一致。不同液膜厚度H*也会影响到液冠高度。图8 展示了不同H*条件下t*=2.5 时液冠高度的变化,当t*=2.5 时,H*由0.1 增加到0.5 过程中液冠高度随着H*的增加而增加,原因在于液滴撞击过程中液柱与液膜之间的夹角减小了,导致水平方向液冠速度增加,而垂直方向上速度减小,液冠半径增长速度也随之增大,但垂直增长速度随之减小。
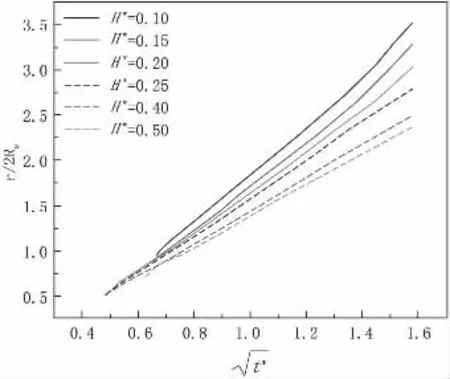
图7 不同液膜厚度H*条件下液冠半径r/2R0 与无量纲时间之间关系
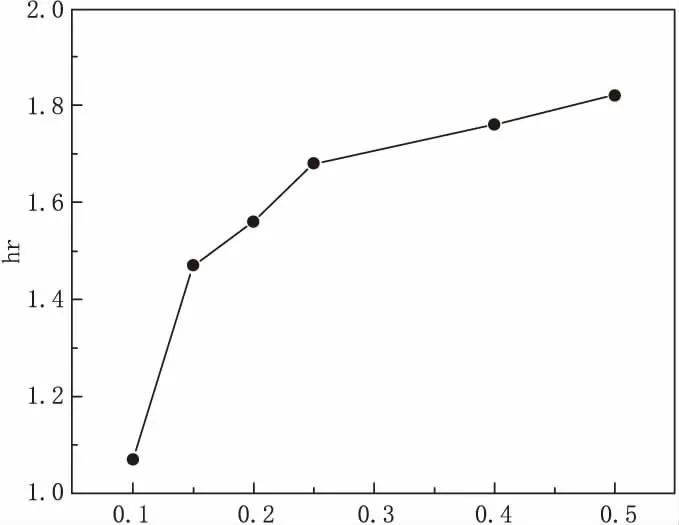
图8 不同液膜厚度t*=2.5 时液冠高度的变化
3 结论与展望
本文采用大密度比LBM伪势模型,结合可调节表面张力的外力项,模拟液滴撞击液膜的过程,并分析不同Re、We 和液膜高度H*条件下,液冠的演化过程,得到结论如下:
1)在相同的液膜高度,高Re 数或高We 数条件下,液冠末端会出现液滴脱离现象,大密度比LBM伪势模型可以有效模拟出此类现象。
2)随着液相粘滞系数增大或液膜厚度H*增加,液冠末端变得越不容易散裂。
3)液滴撞击形成液冠半径与无量纲时间存在线性关系,其斜率随着Re、We 的增大而增大,随着液膜厚度H*的减小而增大。

