基于简化实频法的宽带匹配电路实验教学研究
刘国华,周国祥,郭灿天赐
(杭州电子科技大学 电子信息技术国家级虚拟仿真实验教学中心,浙江 杭州 310018)
在当前5G 通信开始商用的大背景下,射频微波专业技术人才需求旺盛。为了适应行业发展,“微波技术基础”课程教学改革势在必行。阻抗匹配是该课程的重要内容,其作用是将信号源的功率最大不失真地传输到负载,其性能对通信系统至关重要。但阻抗匹配电路概念抽象、理论性强,是公认的教学难点。
经过对多年教学效果的分析,我们对实验环节中的阻抗匹配实验内容进行了改革,将传统的L 型窄带匹配电路设计升级为与当前5G 宽带通信相适应的宽带匹配电路设计,将简化实频技术(SRFT)的科研成果引入实验教学。
1977 年,Carlin 首先提出原始实频法,这是一种基于线性分段近似逼近最佳特性的网络综合方法[1],为宽带匹配网络设计提供了新途径。1982 年,Yarman在原始实频法的基础上,对算法进行了改进,提出了简化实频算法[2],缩短了算法优化时间,使设计更便捷。
国内陈轶鸿、何瑶、武军伟和马银圣[3-8]等学者把实频技术应用到天线的宽带阻抗匹配上,不仅减少了由阻抗失配引起的损耗,还提高了天线的工作带宽和馈电效率。
简化实频法用归一化散射参数来描述无损耗的双端口匹配网络,很适合用来设计微波放大器[9]的输入输出匹配电路。当它与建模技术相结合时,可以为任何类型的宽带匹配问题提供有效的解决方案。
1 简化实频法(SRFT)理论分析
匹配电路性能通常用传输功率增益(TPG)来衡量。TPG[10]的定义是负载输入功率与源输出功率的比值,可以用来描述匹配网络的损耗程度。图1 是用散射参数表示的匹配网络E。

图1 散射参数的匹配网络
任何有界实反射系数E11(s)可由以纯电阻为终端的无耗双端口网络来实现,一旦求出E11(s),即可确定网络E的参数。因此实频法将匹配网络E用s参数表示为:

其中,n代表网络中的元件数。h(s)与g(s)均是n项的赫尔维兹多项式。
根据无耗网络特性,满足如下条件:

最后得出TPG 的表达式为:

其中,EL为负载网络输入反射系数。
最后是构造误差函数Terr(s),使其在整个频段内优化到一个最小值,得到优化后的h与g构建宽带匹配电路:

式中,T表示TPG 值,T(s)为待优化的TPG 值,T0为目标TPG 值。整个实频算法的流程如图2 所示。这个算法可以由MATLAB 编程实现。
该算法的MATLAB 主程序如图3 所示。需要学生在使用该算法前,提前预设目标,包括目标TPG、迭代优化次数、优化频段范围、初始待优化的h等参数。
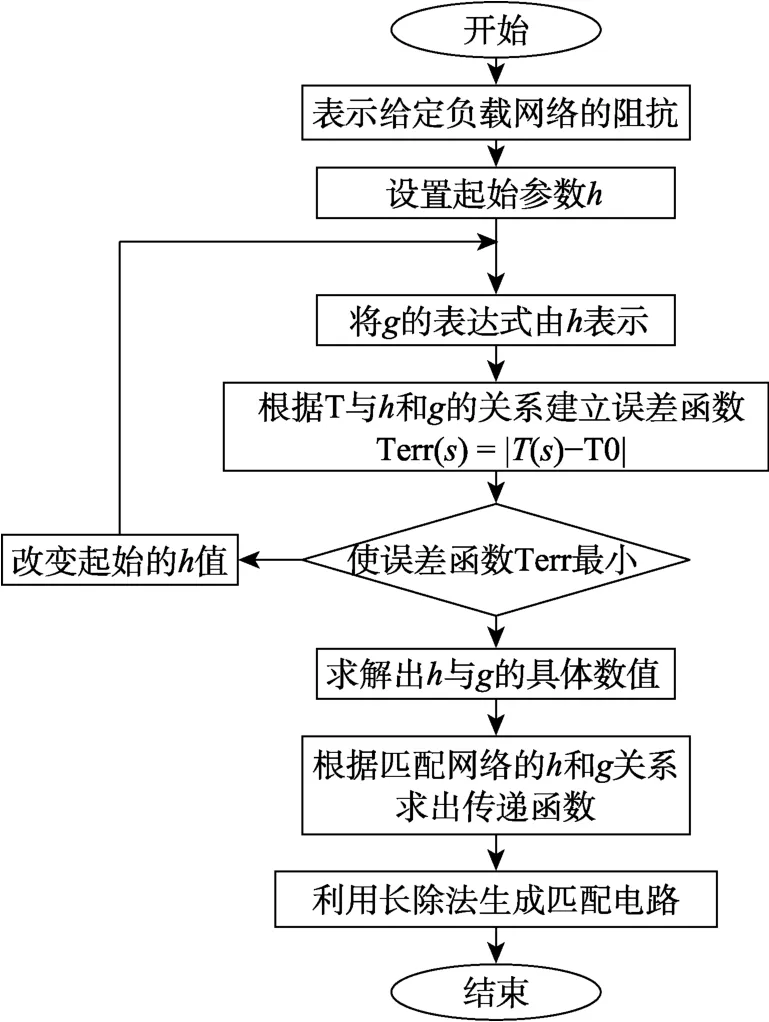
图2 简化实频算法流程图

图3 MATLAB 程序图
2 简化实频法(SRFT)宽带匹配电路设计
作为例子,对图4 所示的负载网络进行宽带匹配电路设计,并将TPG 优化到期望值。

图4 负载网络结构
根据简化实频法理论分析,得出赫尔维兹多项式的表达式后,将匹配网络的输入阻抗Z用长除法进行运算,最终的形式表示为:

然后通过MATLAB 程序,将TPG 的预期值设置为0.75,设置中心频率f0为50 MHz,特征阻抗为50 Ω。最终综合出优化后的匹配电路结构如图5 所示,TPG优化曲线如图6 所示。

图5 优化后的匹配电路

图6 TPG 曲线图
图5 中显示出的是元器件值(无单位),通过公式(10)和(11)进行反归一化求解[11],得到电路器件的实际值。

其中,Cn和Ln为优化得到的归一化值,反归一化后可综合出实际电路,得到整体电路结构如图7 所示。
为了验证算法的有效性和所设计电路的性能,将简化实频法计算结果与两款主流的射频微波电路仿真软件ADS 和AWR 的仿真结果进行比较,激发了学生对匹配电路设计的主动探索兴趣,又能引导学生深入理解优秀仿真软件的电路优化原理。

图7 整体电路结构
3 ADS 仿真优化
将简化实频法中得到的完整电路在射频电路仿真软件ADS 中进行仿真,得出TPG 曲线;再通过ADS的优化工具进行优化,得出的结果如图8 所示。
将优化前后的TPG 曲线进行比较,发现在频率35~65 MHz 内,ADS 优化后的曲线值略低,优化前后的波动程度近似且稳定;在频率25~35 MHz 内,ADS优化后的曲线波动较大,最高值达到0.76,明显高于优化前的曲线值。而在其他频段内,ADS 优化前后变 化不大,近似相同。因此,ADS 优化可以达到简化实频法优化的效果。但是从整体曲线来看,优化前TPG的波动范围在0.7±0.01,优化后TPG 波动为0.7±0.05,有所变大,因此简化实频法在稳定性方面更出色。
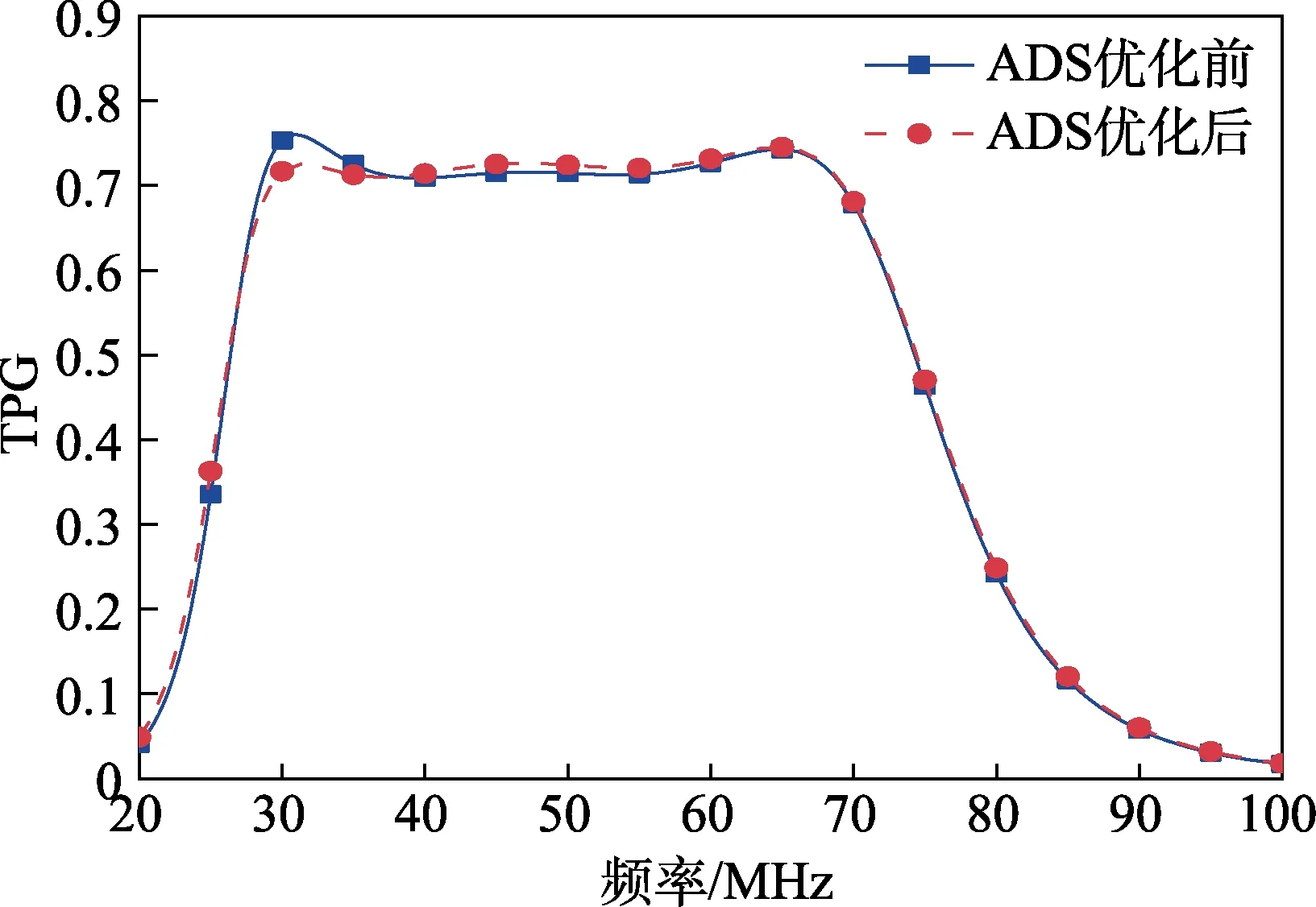
图8 ADS 中优化前后的TPG 曲线
4 AWR 仿真优化
通过AWR 软件自带的优化工具优化后,将得到的TPG 曲线和简化实频法获得的TPG 曲线在同一图中进行比较,如图9 所示。
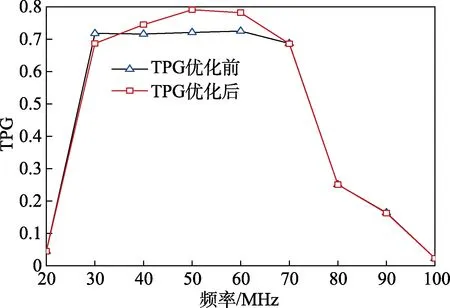
图9 AWR 中优化前后的TPG 曲线
从图中可以看出,在频段35~70 MHz 内,AWR优化后的曲线值明显增加且波动较大,最大值接近于0.8。而在频段30~35 MHz 内,优化后的值略低于优化前。对比显示,AWR 优化后TPG 波动较大,呈现出不稳定性。
5 三种优化方法对比
本文所选的三种优化方法分别是简化实频法中的最小二乘法(least squares)优化、ADS 中随机方式(random)优化、AWR 中共轭梯度方式(conjugate gradient)优化。
其中,简化实频法中的最小二乘法[12]是使待优化参数和目标参数的差值平方和最小,从而实现数据的最优化。ADS 中随机方式优化不需要使用任何数学模型来代入优化参数,通过随机迭代数值,寻找符合目标的解。如果在不要求效率的情况下,随机优化算法可以通过无数次的迭代优化找到最优解。但为了保证一定的效率,实验中使用了迭代次数为50 的随机优化作为参考对比。而AWR 中的共轭梯度优化方式具有较快的优化速度,且具有较高的稳定性。
将三种优化方式的TPG 曲线放在同一图中进行比较,如图10 所示。
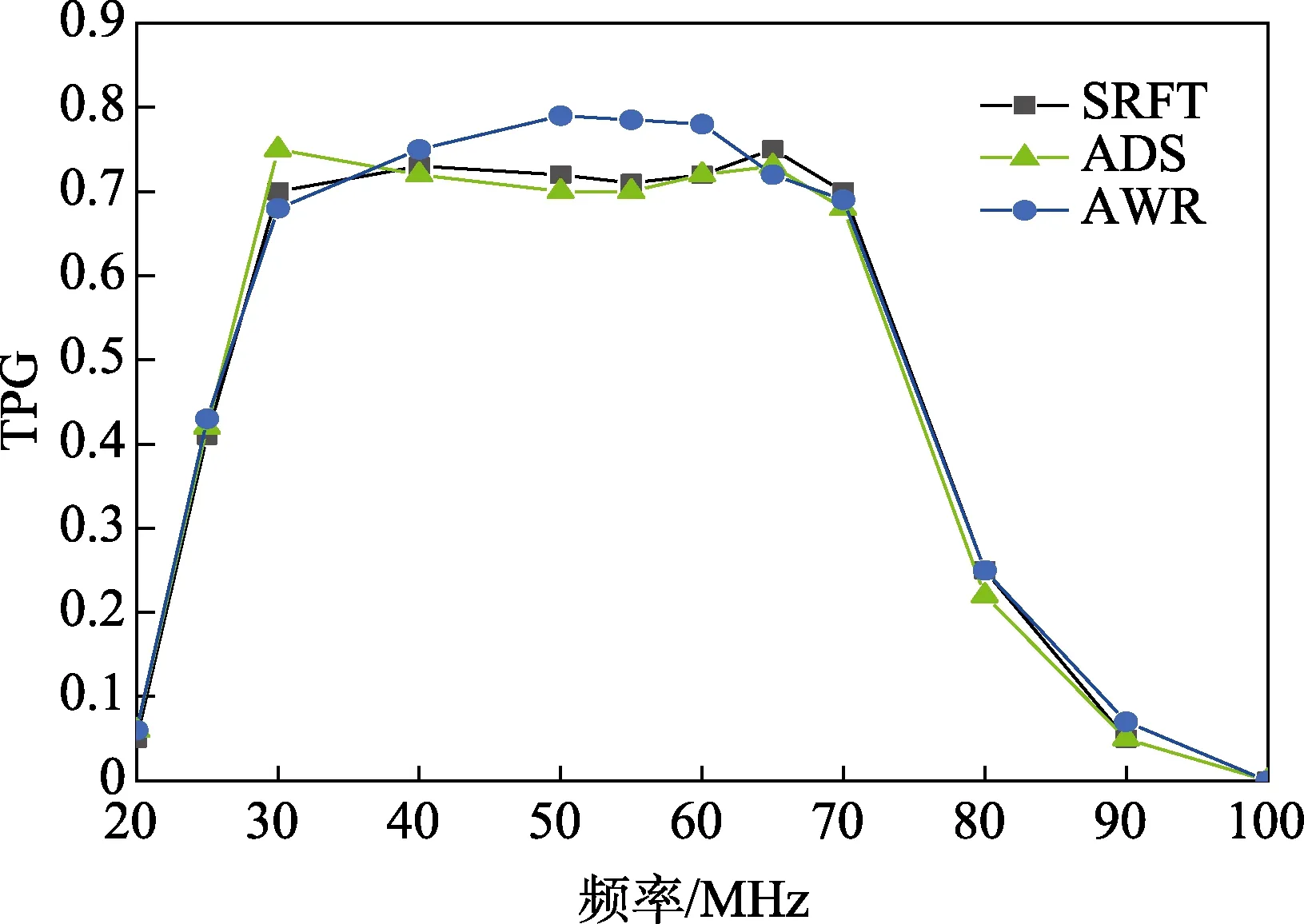
图10 三种优化曲线对比
从图中看出,在频率20~30 MHz 和75~100 MHz两个范围内,三种曲线基本一致。而在30~75 MHz 范围内,三种曲线呈现了不同的趋势。ADS 优化曲线稳定在0.7,AWR 优化曲线最高值达到了0.8,而简化实 频法优化曲线在0.7 与预期值0.75 之间波动,最高值达到了预期值0.75。总体而言,简化实频法优化后的TPG 曲线在通带范围内比较平稳,波动最小,说明该算法与ADS 和AWR 自带优化算法相比,对TPG 的优化效果最好。
从所用时间看,简化实频法、ADS 法、AWR 法分别为0.65 s、6 s 和0.34 s。由于ADS 中进行了50次迭代的随机方式优化,其优化所需时间最长,而AWR 中共轭梯度优化比简化实频法快0.31 s,但其优化的TPG 曲线在带宽范围内波动较大,不能保证优化的稳定性。以上对比分析表明,使用简化实频法设计匹配电路可以得到性能与预期近似且稳定的电路结构。
6 结语
本文将科研成果引入实验教学,用一个宽带匹配网络的设计实例,比较了简化实频法、ADS 软件、AWR软件的设计优化过程及结果,验证了简化实频算法的有效性。由于专业仿真软件内嵌的优化过程不可控,学生在使用时往往知其然而不知其所以然,在实验教学中有局限性。通过自主编写程序设计匹配网络,能够使学生深入体会宽带电路设计的难点及用网络综合法解决问题的高效性,通过改进传统方法解决现实问题,培养了学生的创新思维和实践能力。

