崎岖山地环境履带机器人降维变系数控制方法研究

刘 路 杨 冰 韦 东 宋 宇 陈黎卿 孙 燕,3

(1.安徽农业大学工学院， 合肥 230036； 2.安徽省智能农机装备工程实验室， 合肥 230036；3.安徽省工业节电与电能质量控制协同创新中心， 合肥 230601)

0 引言

近年来，小型履带机器人广泛应用于田间作业中，由于田间路面崎岖不平[1-3]，易造成航向偏差增大。因此，车身侧倾、俯仰对小型履带式机器人的影响成为农田环境下农业导航控制领域不可忽视的因素[4-8]。为解决路面崎岖不平对小型履带机器人的影响问题，国内外诸多学者多采用二维平面滑模控制(SMC)作为位姿控制系统[9-14]，解决了二维平整路面路径跟踪的问题。机器人在三维崎岖路面上的姿态控制误差与机器人行驶过程中的姿态变化有关，需要探索合适的姿态检测及控制修正方法，以提升机器人实时控制精度[15-20]。

针对上述问题，本文以小型履带机器人作为研究对象，设计一种基于降维变系数的滑模控制系统，该系统采用惯导传感器与RTK北斗定位系统，实时检测车身位姿信息，微控制器将理想位姿信息作为降维变系数系统的控制输入，实时匹配两侧履带运行速度，以达到在崎岖路面修正车身航向、提高行驶稳定性的目的。

1 履带机器人系统组成与原理

1.1 履带机器人结构及主要参数

为了实现行距800 mm的垄间精确导航和精准控制，履带机器人的整机结构如图1所示，主要功能包括机器人运行过程中通信、电机驱动和车身控制，相关技术参数如表1所示。

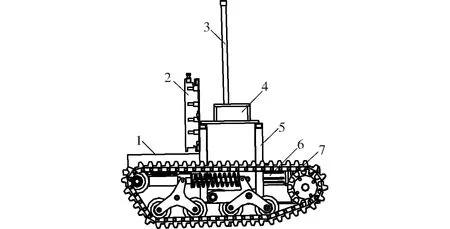
图1 小型履带机器人整机结构简图

表1 小型履带植保机器人主要技术参数

1.2 降维变系数底盘建模方法

机器人在路面上行驶时，地面坐标系为XOY，机器人的局部坐标系xoy中令机器人质心为原点，局部坐标系相对于地面坐标系的位姿可表示为T1，如图2所示。

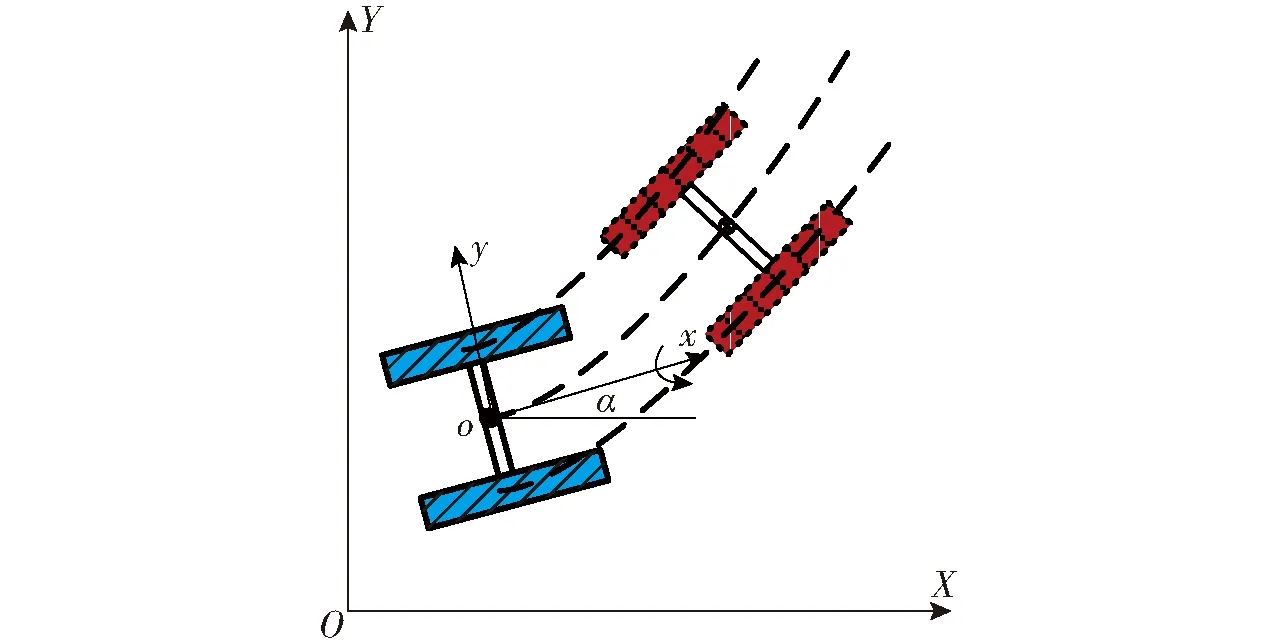
图2 二维平整路面运动简图

图2机器人的二维运动学方程与误差方程为

T1(x,y,α)=N1(α)Q1(v,ω)

(1)

K1(xe,ye,αe)=R1(α)A1(Δ)

(2)

式中T1(x,y,α)——二维机器人位姿

x、y——机器人运动时，x、y轴方向移动距离

α——机器人运动时，局部坐标系x轴与地面坐标系X轴间的夹角，亦称为偏航角

N1(α)——二维实际和理想位姿坐标系转换矩阵

Q1(v,ω)——二维机器人线速度、角速度矩阵

v——线速度

ω——角速度

K1(xe,ye,αe)——二维机器人位姿误差

xe、ye——x、y方向误差

αe——偏航角误差

R1(α)——二维实际位姿和理想位姿误差坐标系转换矩阵

A1(Δ)——二维实际位姿与理想位姿误差矩阵

Δ——二维实际位姿与理想位姿误差

机器人在非平整路面运动时，出现随机的姿态侧向或俯仰变化，二维运动模型的路径跟踪会有较大跟踪误差。为保证机器人的路径跟踪精度，需要对车身上述姿态变化导致的误差进行补偿以实现姿态的修正与位置纠偏。

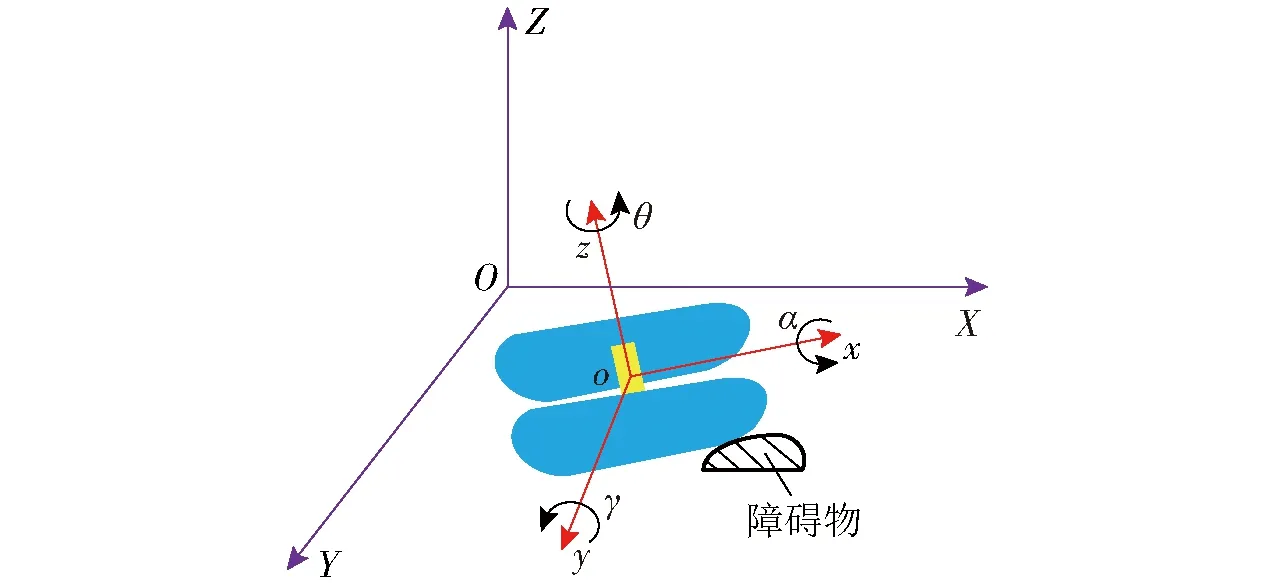
图3 三维崎岖路面运动简图

三维运动模型与二维运动模型相比，增添垂直于地平面方向的Z轴，如图3所示。降维模型利用机器人实际三维空间位姿与理想三维空间旋转映射关系，使机器人运动过程中通过对映射后的轮距、航向的投影参数修正将控制模型始终保持在地面坐标系XOY平面内，从而去除控制模型中z轴方向变量，θ、γ为机器人运动时自身所处的局部坐标系中z、y轴分别与地面坐标系中Z、Y轴的夹角，即横滚角与俯仰角。其自身所处的局部坐标系原点相对于地面坐标系的位姿表示为(x,y,z,α,θ,γ)，因此其降维变系数模型、运动学方程与误差方程为

U(xe,ye,αe)=f(θ,γ)

(3)

T2(x+xe,y+ye,α+αe)=N1(α)f(θ,γ)Q1(v,ω)

(4)

K2(xe,ye,αe)=R2(α)f(θ,γ)A2(Δ)

(5)

式中U(xe,ye,αe)——投影参数修正函数

f(θ,γ)——空间旋转映射函数

T2(x+xe,y+ye,α+αe)——三维机器人位姿

K2(xe,ye,αe)——三维车身位姿误差

R2(α)——三维实际位姿和理想位姿误差坐标系转换矩阵

A2(Δ)——三维实际位姿与理想位姿误差矩阵

上述降维变系数中，将图3所示三维状态下机器人位姿通过映射投影的方法获得理想位姿。在映射投影过程中，姿态发生变化产生二维平面位姿误差，因此，采用投影参数修正函数U(xe,ye,αe)通过映射函数f(θ,γ)对产生的误差进行补偿，进而消除z轴方向与θ、γ波动对跟踪精度的影响。三维运动学模型T2在映射函数f(θ,γ)的补偿下进行二维控制，最终达到降维控制的目的。

2 降维变系数控制方法

在降维运动学几何模型基础上，设计基于降维变系数的位置控制外环、偏航角控制内环、满足机器人运动约束条件的控制策略，实现机器人对于位置、姿态的精确控制，同时实现在崎岖非平整路面上平稳行驶的功能。

2.1 纠偏系统工作原理

本文所研究的双轮差速转向履带机器人，通过控制两驱动轮的转速对车身姿态与理想轨迹进行调节与跟踪。机器人实际位置信息作为控制输入，其线速度与角速度作为控制输出，通过理想路径与实际路径的误差反馈，由纠偏控制系统消除理想位置与实际位置的误差，最终实现路径跟踪。

上述闭环系统属于双环滑模控制系统，其中姿态控制系统为内环，位置控制系统为外环。位姿信息在控制律p1、p2、p3和p4的控制下通过降维变系数模型传递给内外环控制，完成对线速度、角速度的控制，最终达到路径跟踪的目的。其控制流程图如图4所示。

图4 降维变系数控制系统流程图

2.2 降维变系数控制系统组成

降维变系数控制系统由STM32F407ZGT6型微处理器、MTI-G-710型惯导传感器、ZM-6615型直流无刷电机驱动器、直流无刷电机等组成，如图5所示。其中，惯导传感器提供姿态信息，RTK北斗定位系统提供位置信息，上位机根据控制模型输出控制变量，输出的控制变量通过运动控制器将线速度、角速度信息转换成左右履带轮电机转速，最终两轮差速运动实现路径跟踪。

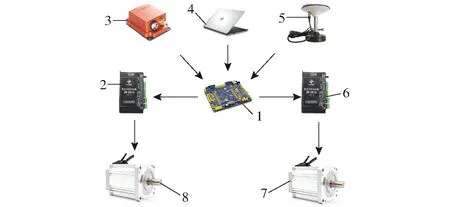
图5 控制系统组成与结构

2.3 降维变系数控制系统设计

2.3.1位置外环控制律设计

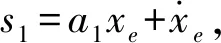
(6)

上述位置控制系统中p1在x方向的子系统控制律为p1x

式中q1——波动量λ1、a1、η1——控制参数

由此可以得到

(7)

若系统趋于稳定，则x方向线速度为

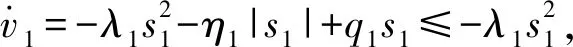
同理，针对y控制系统，设计控制律为

(8)

式中λ2、a2、η2——控制参数

p1y——在y方向的位置子系统控制律

s2——在y方向的滑模函数

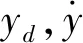
2.3.2偏航角内环控制律设计

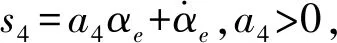
(9)

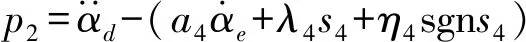
(λ4>0,η4>0)

式中q4——波动量

得到

若系统趋于稳定，则需要x方向线速度为

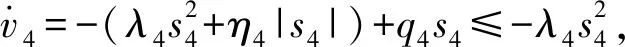
同理，针对θ、γ控制系统，其控制律为

(10)

(11)

从而实现s5、s6指数收敛，θ、γ收敛于理想姿态θd、γd。最终实现履带机器人对理想姿态曲线的角度跟踪。

由于独立的外环控制在位置跟踪过程中易受到姿态波动的影响，产生跟踪误差大、稳定性差的情况，因此引入偏航角内环控制，通过内环收敛速度大于外环收敛速度的方法，确保整个降维变系数控制系统的稳定。

3 仿真试验

为了验证降维变系数控制方法可在二维路面上进行精确跟踪，以双轮差速转向模型作为仿真对象，在Matlab/Simulink环境下进行二维平整路面路径跟踪仿真试验。二维路径追踪试验中，初始位置与姿态设为(0,0,0,0,0,0)，设置理想路径为

(12)

表2 二维仿真相关参数

在此平面路径下，进行二维路径仿真跟踪时，由于不存在z轴数据，故而仅需仿真x、y轴误差与追踪α即可。仿真结果如图6所示。

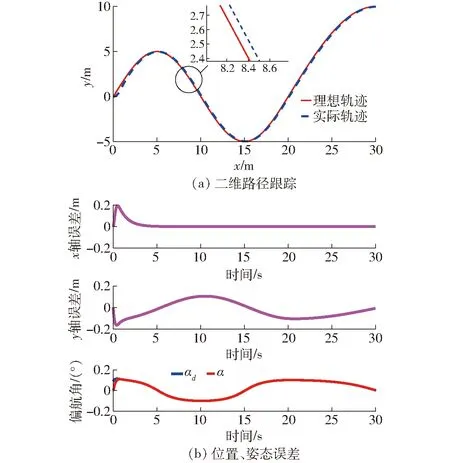
图6 二维路径跟踪仿真结果

二维路径仿真结果表明，二维平整路面路径跟踪过程中，x轴误差在初始的0～2 s内便逐渐减少至0。y轴误差始终控制在±0.2 m之间，偏航角最初的1 s内精确跟踪了理想角度。

为了验证降维变系数控制方法在三维崎岖路面跟踪的精确性，进行三维路径跟踪仿真试验，具体仿真参数如表3所示。

考虑到路面起伏，取理想路径函数为初始位置与姿态设为(0,0,0,0,0,0)。

(13)

表3 三维仿真相关参数

三维路径跟踪仿真结果如图7所示。图7a表明，履带机器人可精确跟踪二维平整路面理想轨迹，结合图7b欧拉角追踪，表明机器人在跟踪上理想偏航角αd后，便无较大范围的波动。在三维路面的顶点或坑底等角度瞬间变化时，降维变系数控制方法能在1 s内快速地跟踪理想的偏航角、滚动角和俯仰角。

结合图7a与图7c可以看出，由于起始点位置设为原点，故而在0～6 s的初始阶段x、y、z轴存在较大的误差。6 s后，随着时间的增加，三轴位置误差逐渐减小，直至误差在±0.1 m内波动。

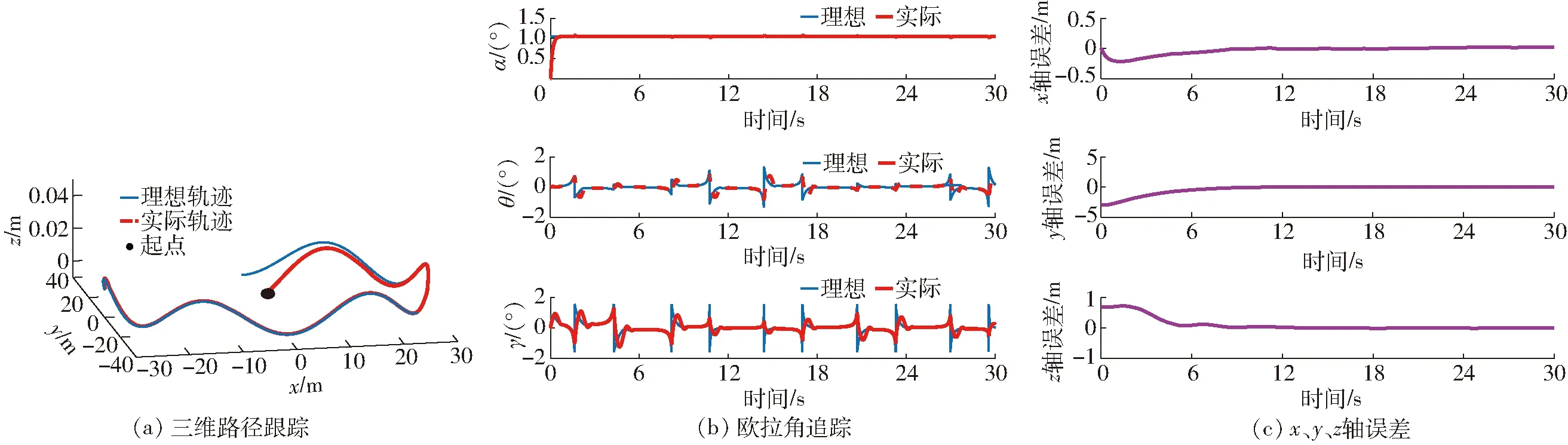
图7 三维路径跟踪仿真结果

二维平整路面与三维崎岖路面相比，二维平整路面仿真时将a4、a5、a6、λ4、λ5、λ6设置为0，仅改变剩余的控制参数，记录机器人的路径跟踪结果，仿真结果表明二维路面和三维路面误差均满足实际需要。

4 降维变系数控制试验

为了验证本文方法的可行性，以安徽农业大学安徽省智能农机装备工程实验室研制的履带机器人作为试验平台，试验环境为非硬化崎岖路面和硬化平整路面两种，设计车速为1.5 m/s。对理想的二维平整路面与三维崎岖路面进行路径跟踪田间试验，如图8所示。

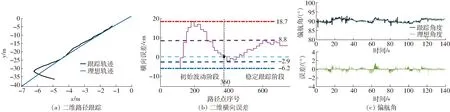
图9 二维平整路面路径跟踪试验结果

图8 田间试验

二维平整路面试验结果如图9所示。图9a中，在理想轨迹与实际轨迹第2次相交时可认为机器人由初始波动阶段进入稳定跟踪阶段。如图9b所示，在平面上跟踪时，其初始波动阶段的横向误差在-6.2～18.7 cm之间，在路径点为360时，机器人处于稳定跟踪，其误差在-2.9～8.8 cm内波动。偏航角跟踪如图9c所示，其跟踪误差在±2°之间，符合控制要求。

崎岖路面试验结果如图10与图11所示。其中，图10a为本文崎岖路面下行驶轨迹与路谱图；图10b与图10d分别为图10a在xy平面与z轴方向投影的跟踪图。如图10b与图10d所示，本文所提出的降维变系数控制系统能够较好地追踪目标路径；在实际轨迹与理想轨迹第4次相交时，机器人由初始波动阶段进入稳定跟踪阶段，其跟踪误差如图10c所示，横向误差在初始波动阶段的误差范围为-23.6～52.7 cm，在路径点序号为381时，由初始波动阶段进入稳定跟踪阶段，机器人在稳定跟踪阶段的误差范围为-14.3～21.5 cm，都处于合理的控制范围内。俯仰角、横滚角与偏航角分别如图11所示，其控制波动皆在±5°以内。

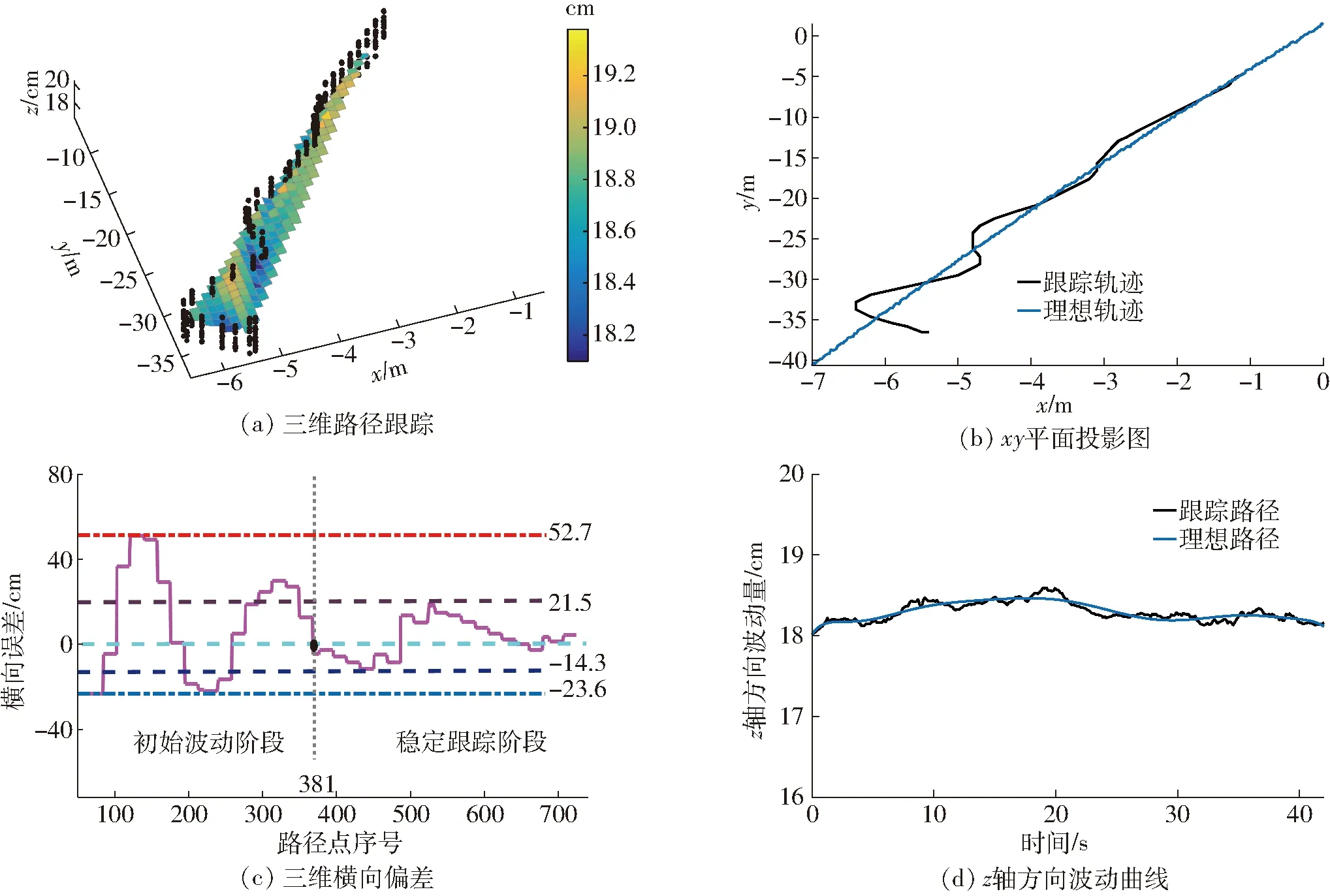
图10 三维崎岖路面位置跟踪试验结果

图11 三维崎岖路面角度跟踪试验结果

5 结论

(1)采用数学建模方法建立了三维运动学模型与误差方程，基于此设计了一种崎岖山地环境下的履带机器人降维变系数控制系统。

(2)Matlab环境下的仿真结果表明，所提出的控制方法能够对履带机器人进行有效的控制，并且能够对理想路径进行有效的跟踪。其二维平整路面仿真结果表明，x轴误差逐渐减少为0，y轴误差控制在±0.2 m范围内，航偏角在1 s内完成跟踪理想角度；三维崎岖路面仿真结果表明，三轴姿态角在1 s内完成对理想姿态角的跟踪，同时三轴误差都控制在±0.1 m内。因此，在仿真阶段能够满足履带机器人保持在800 mm宽作物行内的行驶要求。

(3)履带机器人在二维平整路面上进行路径跟踪时，其横向误差在初始波动阶段波动范围在-6.2～18.7 cm之间，机器人处于稳定跟踪时，其误差在-2.9～8.8 cm内波动，姿态角在±2°范围内波动。在三维崎岖路面上，采用降维变系数控制方法能够对理想路径进行有效跟踪，机器人横向误差在初始波动阶段范围为-23.6～52.7 cm，在稳定跟踪阶段范围为-14.3～21.5 cm，姿态角控制在±5°范围内。说明履带机器人能够保持在800 mm宽作物行内的正常行驶。