基于改进ARMA模型的火箭发动机稳态工况过程实时故障诊断方法研究
(北京航天动力研究所,北京 100076)
0 引言
作为基于数学模型的故障诊断方法中的一种,时间序列分析方法的优点是具有良好的鲁棒性、实用性和实时性。而在时间序列分析方法中,应用于液体火箭发动机故障检测与诊断中应用的主要是AR模型和ARMA模型。
国内外就时间序列分析方法也做了大量的研究。1990年,文献[1]以SSME为研究对象,对其运行的全过程都应用了ARMA模型进行故障诊断,并与红线关机算法进行了比较,体现了其快速性及实用性;1997年,吴建军等[2]提出了基于ARMA模型计算残差自相关函数置信区间检验的故障检测策略,并介绍了相关建模方法;2002年,张纯良等[3]通过改进ARMA模型,实现了对某空间推进系统的故障特征参数提取;2019年,薛薇等[4]针对重复使用的液体火箭发动机,设计了基于ARMA模型的实时故障仿真系统,对典型故障进行了仿真测试,并通过硬件在回路仿真测试,验证了算法的适用性。
综上所述,国内外有关于ARMA的研究有很多,但是绝大部分都是关于ARMA模型的训练,包括模型识别和参数估计等方面,而关于故障阈值的计算,故障的判断准则的研究却几乎没有。本文以大推力氢氧补燃循环发动机为研究对象,采用了基于改进ARMA模型进行故障诊断,利用改进的阈值计算方法以及连续准则对它主级工况下故障进行了实时诊断,诊断结果良好。
1 基于ARMA模型的故障诊断
1.1 ARMA模型概述
ARMA(p,q)[5]自回归滑动平均模型是研究时间序列的一种最为重要的分析方法,该方法认为在一组平稳的时间序列中,某一时刻的观测值不仅和前p步的观测值有关,还和前q步的扰动有关,且均为线性关系,它的表达式如式(1)所示:
(1)
其中:φi为自回归部分系数,θi为滑动平均部分系数;p和q分别为自回归阶数和滑动平均阶数;xt为t时刻的观测值,at为t时刻的偏差。特殊的,当p=0时,模型即为移动平均模型,记为MA(q),当q=0时,模型即为自回归模型,记为AR(p)。
ARMA模型所研究的是有序时间序列数据的一个内在联系,不需要考虑影响数据的各外在因素,通过分析有序数据本身的一个规律,来进行短期的预测。当给定一组系统的时间序列时,通过训练建立ARMA模型,可以得到短期的预测数据,将预测数据与实际数据相互比较,可以判断系统是否出现故障。ARMA模型使用有一个重要的前提,即所分析的数据必须是平稳数据。
1.2 ARMA模型的训练
利用时间序列训练ARMA的主要步骤如图1所示,首先是读入数据,利用传感器测得所需要的参数数据,然后进行数据的处理,接着进行模型识别和参数估计,最后进行模型的检验和预测。
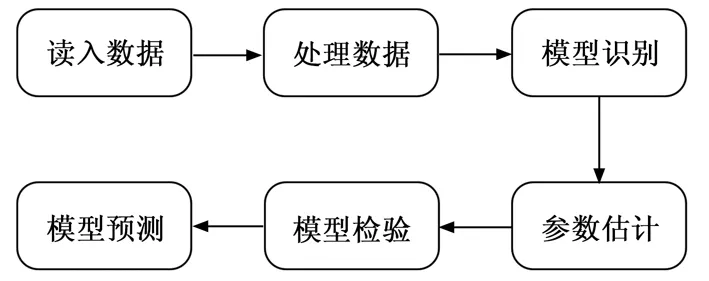
图1 ARMA模型训练步骤
首先,判断原始数据是否平稳,如不平稳,则进行差分处理,使其平稳,这是因为ARMA模型只能训练平稳的数据;接着进行模型识别,判断适用于ARMA模型、AR模型还是MA模型;然后通过相关定阶及参数估计方法确定模型阶数和参数,确定模型具体表达形式;最后进行预测和检验,如果不合适,则重新进行模型的训练过程。
训练ARMA模型时,最为重要的就是模型定阶及参数估计的部分,模型阶数和参数的准确性直接影响到检验结果的好坏[6]。本文确定模型阶数的方法为:首先通过分析计算时间序列的自相关函数ACF和偏自相关函数PACF及它们各自的图像,利用它们的拖尾性和截尾性实现模型阶数的初步确定,得到模型阶数的几种组合情况,接着利用AIC信息准则,选择AIC值最小的模型作为最优的模型阶数。而当模型的阶数确定之后,便需要进行参数估计,模型参数估计的方式有很多,最常见的方法有:矩估计法、极大似然估计法、最小二乘法等等,本文利用最小二乘法进行参数估计,最后得到准确的预测模型。
ARMA模型所针对的只是一个监测参数,当需要对多个参数进行判断时,则需要针对每一个参数单独进行模型训练,即有多少个监测参数,就需要训练多少个ARMA模型。
1.3 基于ARMA模型的发动机稳态工况实时诊断算法设计
当液体火箭发动机工作在主级工况下时,各监测参数都会稳定在一定的动态范围内,我们利用这些参数来训练ARMA模型,可以预测参数的一个变化规律。当发动机故障发生,我们用模型预测得到的数据和实际数据就会有很大偏差,但这个残差到达什么程度则判定为故障的研究却很稀少,国内外学者们就ARMA模型在故障诊断上的应用有很多的研究,但是大多都是针对如何进行训练模型而展开,本文基于改进ARMA模型的判断准则出发,使用了新的阈值计算方法以及连续判定准则,实现了故障的零误报率及快速报警。
一般而言,基于信号和模型的故障诊断算法,判断故障是否发生主要依靠于阈值准则,即当预测值和实际值之间的偏差量大于某一阈值时,则判断故障发生。在本文中,为了避免因为偶然因素导致某一瞬间参数变化过大,从而导致误判的情况,采用了连续准则,即当预测值和实际值之间的偏差量连续几次超过某一阈值,则判断故障发生,反之,则未发生,并通过多次试验,发现当连续次数设定为二次、三次和四次时,系统均会出现误报警,而当连续次数设定为五次时,诊断情况最为精确,无误报警出现,所以设定连续次数为5次。
参数阈值的设定对算法的灵敏度和可靠性的影响很大,如果阈值设定过低,则易出现误报警,如果阈值范围太大,又会降低算法的灵敏度。我们的改进阈值确定方法参考自适应相关安全限故障检测算法阈值的设定准则[7],在主级工况下,参数的阈值计算公式如下:
Pt=Pave+S*N
(2)
其中:Pt为参数的阈值,Pave为参数的平均值,S为参数的标准偏差,N为带宽系数。Pave和S由主级工况下各参数正常工作的统计数据求得,而带宽系数N根据正常参数测量值位于安全带之外的概率来确定。具体确定阈值的方法如下:
1)首先计算前n个样本数据的平均值Pave和标准偏差值S;
2)接着先令带宽系数N值为1,初步确定参数阈值,并记录前n个样本数据中参数值超过阈值的参数值P及次数M;
3)利用式(3)计算越界参数的规范化偏差值的平均值N′:
(3)
4)确定阈值公式如式(4)所示:
Pt=Pave+S*(1+N′)
(4)
改进的阈值求解公式计算得到的阈值与传统的阈值求解算法相比,通过实验验证,发现误报警率有明显的降低,故障诊断效率有明显的提高。
2 基于改进ARMA模型判别准则的的发动机典型故障分析
2.1 故障模型和故障数据

图2 氢氧补燃循环发动机仿真系统图
本文的故障模型来源于我国新一代大推力氢氧补燃循环液体火箭发动机,它以低温液氢液氧作为推进剂,采用了单富氢预燃室,燃气并联驱动氢氧涡轮泵的补燃循环方案。本文利用了Matlab/Simulink工具构建了它的故障仿真模型,具体结构如图2所示,它可以仿真发动机各部位多种典型故障,并支持发动机模块化的建模功能,详细的设计及仿真分析见文献[8]。
发动机在主级工况时,各监控参数都稳定在一个合理的动态范围内,发动机正常工作时,这些波动是可以预测的,变化的这些参数可以通过相应的传感器测量得到,当发动机有故障发生时,这些参数就会出现较为明显的变化,传感器测量的参数也会超出稳态工作范围。本文主要利用改进ARMA模型来实现发动机主级工况的实时故障诊断研究。
一般而言,给发动机仿真模型添加故障有两种方式:一种是修改发动机系统仿真模型,直接构建新的故障模型;另一种是可通过添加相应故障故障因子的方法,在发动机模型上直接乘以一个故障因子数,故障因子的设置部位和大小反应了故障发生的部位和故障严重程度。考虑到第二种方法的易操作性和可靠性,我们选择添加故障因子的方法来构建发动机故障模型。本文添加的故障类型为主氧泵汽蚀故障,当发生这类故障时,首先氧泵汽蚀会直接导致氧泵效率的明显的降低,相应的氧泵的关键参数诸如转速、出口的压力和流量也会降低;接着根据发动机的工作原理以及氧工质流动情况分析,主氧泵连接了氧预压泵和预燃室,氧流量互通,压力相互平衡,从流量关系来看,导致了氧预压泵流量、推力室氧喷前流量和推力室喉部流量的明显降低,而从压力关系来看,主氧泵出口压力的降低,引起了主氧泵泵前压力和推力室氧喷前压力的下降。而其它发动机关键参数变化,由于发动机的耦合关系,也会出现相应的变化。
通过上述的故障模式分析,得到了关键参数的变化情况,对于我们下一节发动机监测参数的选择有着重要的参考价值。
2.2 训练ARMA模型
每一个监测参数都需要训练对应的ARMA模型,所以监测参数的选择极为关键。根据上一节的故障模式分析结果,并结合了监测参数的可监控性、监测参数对故障的敏感性、监测参数对于监控算法的强鲁棒性等方面[9]选择了氧主泵泵后流量、氧主涡轮泵转速和氧主泵泵后压力这三个监测参数,表1列出了所选择的监测参数以及单位。
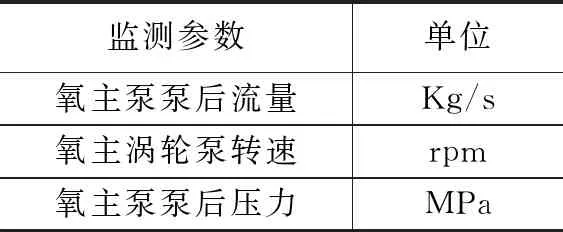
表1 用于ARMA模型训练的氧泵汽蚀监测参数
本文设置仿真总时间为7 s,而故障发生时间则为4 s,设定的采样步长为0.01 s,并增加了高斯白噪声。首先通过仿真得到了氧泵汽蚀故障三个监测参数的原始数据图及零均值之后的图如图3所示。
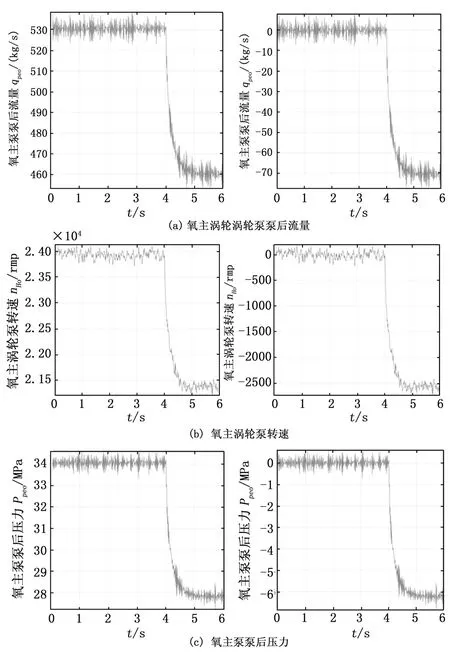
图3 参数原始数据图和零均值图
根据直接观测,正常工作时候的数据无明显的周期变化,并且没有明显的趋势性,说明数据具有平稳性,则零均值化之后的数据也是零均值平稳时间序列,满足了ARMA算法建模的要求,可以用于ARMA算法建模,并进行数据的预测和分析。
接着我们利用这三个监测参数正常工作时的数据来进行ARMA模型的训练,而用于ARMA模型训练的数据长度也有一定的要求,训练长度过长时,会使得计算量增大且易导致模型训练的困难,而当训练长度过于短时,则会使得所选数据不能完全表示数据的特征,导致训练的模型准确度不够。因此,一般模型数据长度的选择需要经历试验来验证。这里我们分别使用了正常工作时的前200个、前300个以及前400个数据来进行模型的训练,发现前200个数据得到的模型差距太大,而前300个和前400个数据得到的训练模型几乎一样,所以在考虑到准确性和为了减少计算量的情况下,选择利用前300个数据来进行模型训练。首先进行模型识别步骤,分别计算并画出前300个数据的自相关函数值和偏自相关函数值,如图4所示。
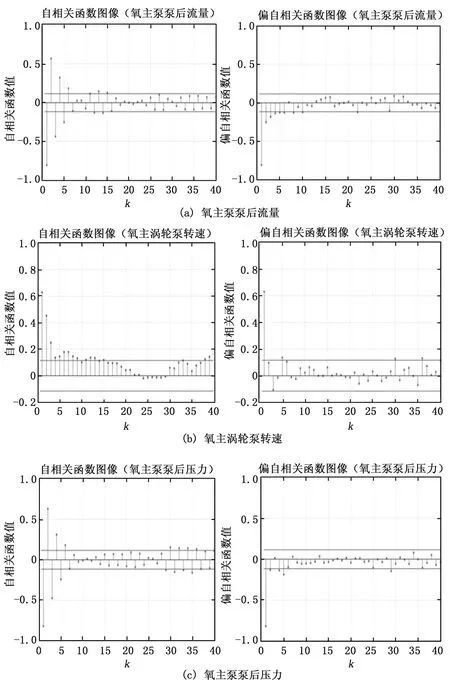
图4 自相关函数图像和偏自相关函数图像
由于样本数据的ACF大多都落在了置信区间内,满足随机性要求,并且随着k增大,函数值逐渐趋近于0,则认为该序列具有平稳性,可以按照ARMA模型进行预测分析,下面分别针对三个监测参数建立各自的ARMA模型。
针对氧主泵泵后流量,分析图4(a)的图像:根据偏自相关函数图的拖尾性,我们可以确定自回归阶数p值为1,而根据自相关函数图像的拖尾性,我们可以确定滑动平均阶数q值为4、5和6。因此我们可以初步得到ARMA(1,4)、ARMA(1,5)和ARMA(1,6)这3个模型。接着利用AIC信息准则,分别计算这3个模型所对应的参数以及AIC值,如表2所示。
根据AIC准则,选择AIC最小的对应的模型作为最优模型,最终确定预测模型为ARMA(1,4),因此可以得到氧主泵泵后流量的预测模型如式(5)所示:
xt=-0.77759*xt-1+at+0.35776*at-1+0.206652*at-2+ 0.0569704*at-3+0.057282*at-4
(5)
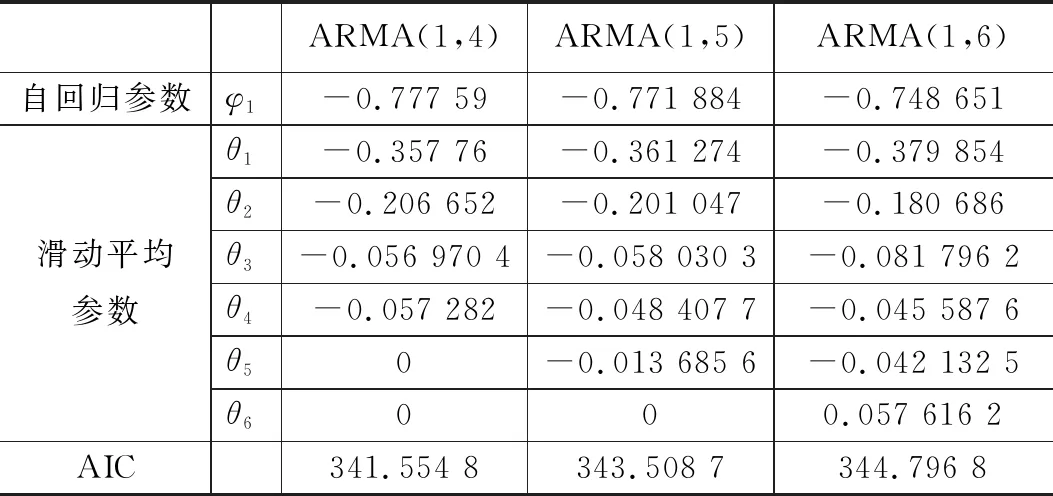
表2 模型参数的拟合结果
同理,针对氧主涡轮泵转速,得到预测模型如式(6)所示:
xt=0.855249*xt-1+at+0.324822*at-1-
0.00513586*at-2+0.194542*at-3
(6)
同理,针对氧主泵泵后压力,得到预测模型如式(7)所示:
xt=-0.780675*xt-1+at+0.201901*at-1+
0.00949483*at-2+ 0.125835*at-3+0.214167*at-4
(7)
2.3 改进ARMA模型判别准则的故障诊断与分析
2.3.1 模型精度分析
三个监测参数都有了预测数学模型,接着根据各自的预测模型,我们可以做出各自的预测曲线,并将它与实际曲线相比较,如图5所示,左侧为预测曲线和实际曲线对比图形,右侧为预测值和实际值得差值图。
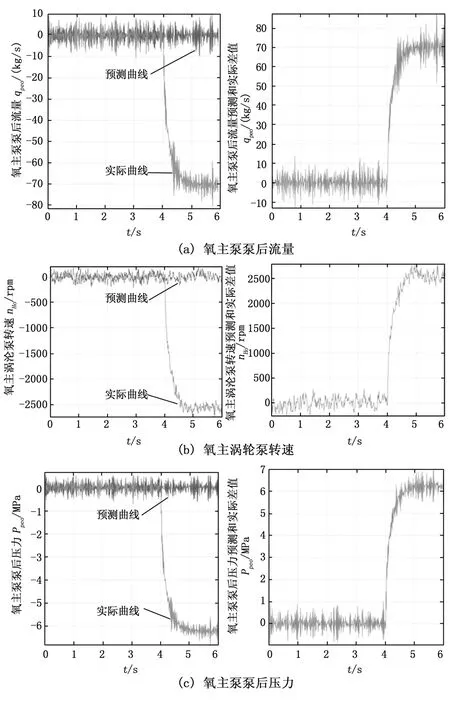
图5 预测结果图
根据图5左侧图形观察可以知道,预测图形和实际图形基本重合,预测效果良好,并且在故障发生后,3个监测参数都有了明显的下降,这和我们之前预测的故障参数变化趋势一致,这也证明了搭建的发动机故障仿真模型是正确的;右侧图形可以发现,实际值和预测值得差值相比于实际值较小,证明了预测结果精度较高。而对于时间序列模型的预测效果来说,预测的精度是极为重要的,接下来我们通过相关数值来让结果更加清晰明了。目前,对预测的精度评定主要是基于误差理论[10],即用平均绝对误差(Mean Absolute Error, MAE)和均方误差(Mean Squared Error, MSE)来衡量。本文选择平均绝对误差MAE作为模型预测精度的判断标准,通过Matlab编程得到了三个监测参数MAE值如表3所示。
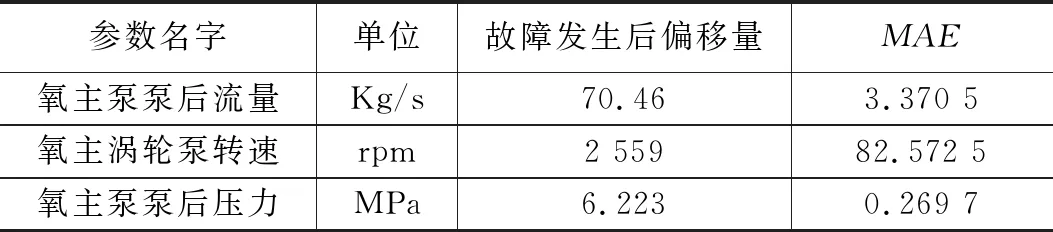
表3 监测参数MAE值
通过表3分析可知,三个监测参数的平均绝对误差和发生故障后的偏移量相比较小,数值上连5%都不到,所以故障发生之前,监测参数的正常波动并不会影响训练的ARMA模型对故障发生的判断,可以用于判断故障是否发生。
2.3.2 基于改进阈值判别准则的故障诊断
我们利用前300个正常工况下的预测值和实际值的偏差值来进行发动机故障的诊断分析,首先基于改进的参数阈值求解式(2)~(4),确定了各监测参数预测值和实际值差值的阈值,然后设定连续超过阈值次数为5次时报警,并选取这五次中第一次的时间为发生故障的时间,最后通过仿真分析,得到了氧泵汽蚀故障下各监测参数的故障诊断情况如表4所示,上述过程均利用了Matlab编程[11]实现。
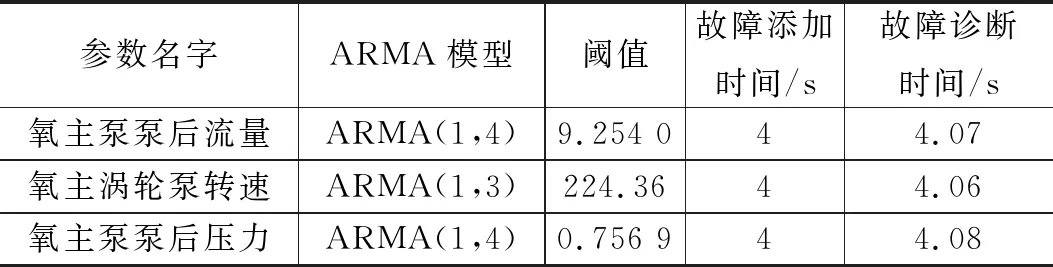
表4 各参数的故障诊断情况
由表4结果分析可知:3个监测参数均未出现提前的误报警,诊断时间都在几十毫秒的量级,每一个参数都能迅速地诊断出故障,设定的阈值合理,故障诊断较为迅速。这些均证明了所训练的ARMA模型以及所使用的改进阈值判别准则和连续准则合理且高效,可以用于发动机故障诊断,这对于以后发动机健康监控系统的设计有着积极的参考意义。
3 结论
本文重点针对新一代大推力氢氧补燃循环液体火箭发动机主级工况进行了实时的诊断算法设计,并通过仿真分析验证了算法的有效性。首先,通过MATLAB/Simulink工具建立了大推力氢氧补燃循环发动机的故障仿真模型,并通过添加故障因子的办法得到了对应故障模式的原始故障数据;其次,设计了改进的ARMA模型,并改进了阈值求解算法和故障判别准则;最后,通过仿真分析验证了所训练的算法的合理性以及改进阈值判别准则的高效性及适用性,满足发动机故障诊断系统设计的要求。

