船体阻力数值预报研究及黏性流场计算

王英第，陈彦臻，周伟健，张盛龙

(1. 渤海船舶职业学院 船舶工程学院，辽宁 葫芦岛 125001；2. 上海海事大学 商船学院，上海 201306；3. 哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001；4. 常熟理工学院 汽车学院，江苏 常熟 215500)

0 引 言

自从能效设计指数（EEDI）标准实施以来，学者们纷纷开始关注船舶的能源利用和环境保护问题。在船舶运营中，燃料的消耗不仅和能源利用、环保等问题息息相关，燃料成本也是公司的巨大开销之一。因此，设计出阻力更小的船舶以减少船舶运营成本、提高燃料利用效率，成为各国船舶研究人员的共同目标。能够在设计阶段准确预报出船体阻力变得非常重要。

随着计算机技术的高速发展以及数值理论的日益成熟，昂贵的船模实验开始渐渐被建立在仿真基础上的设计方法所替代。近年来计算流体力学（CFD）方法得到了广泛的认可，随着许多优秀的CFD软件如Fluent、CFX、SHIPFLOW等在工程问题中被大量应用，CFD方法体现出了其巨大价值，也使CFD方法应用于船舶阻力预报成为可能[1-3]。CFD方法能够获得与试验数据相符的计算结果，同时计算周期短，成本低廉[4-6]。近年来，CFD方法已经成为计算船舶阻力的一种有效途径，有相当多的CFD方法被应用在船体阻力预报中，基于CFD的数值计算成为一种新的经济、高效的研究船舶水动力性能的工具。倪崇本[7]采用基于CFD理论的动网格技术对某多体船进行了数值模拟，探讨了多体船船体姿态对船体表面压力及船体附近波形等方面的影响。张艳等[8]利用CFD方法算得船身周围水压分布情况，并预测了水流对船舶产生的航行阻力。孔金平等[9]用CFD软件对双螺旋桨系统进行了数值计算，并采用湍流模型预报螺旋桨的水动力性能。

为了准确预报船体阻力，首先以自由模为例，讨论了边界层划分方式及湍流模型中系数的选择对阻力预报的影响。然后，在合适的网格方式上，采用NLPQL方法建立基于湍流系数的阻力优化系统来获得最佳湍流系数。其次，根据最合适的网格划分方式及数值计算方法模拟不同航速下KCS船在海面上的水动力性能，讨论约束模和自由模在流场捕捉及阻力预报方面的差异。

1 CFD数学模型建立

整个CFD数学模型的流场控制方程由连续方程和运动方程构成。采用Realizable k-ε模型作为整个流场的湍流模型。采用VOF[10]方法精确捕捉自由水平面，VOF法是一种在固定的欧拉网格下的表面跟踪方法，通过求解动量方程和一处或多处流体的体积分数来模拟多项流模型。采用SIMPLE法对压力场和速度场进行耦合。

为了精确模拟KCS船在海面上的运动情况，将船体纵摇和垂荡运动添加到阻力预报之中。在建立船舶运动方程时，建立2个参考坐标系：一个是固定于大地的固定坐标系，另一个是固定于船体的随船动坐标系，其中动坐标系的原点在船体的重心处。

2 几何模型及网格划分

本文以KCS船型作为研究对象，该船的主尺度如表1所示。

整个计算域尺度设置为5Lpp×3Lpp×4Lpp。为了减小网格数量，取半船作为研究对象。在水池入口边界给定船体航行速度，水池两侧设为对称边界，水池顶部和底部设为速度入口，出口处设为压力出口，边界条件设置如图1所示。

切割体网格技术同时包含了非结构网格和结构网格的优点，对模拟大幅度物体运动问题具有较高的计算精度，是一种新发展起来的网格生成技术。本文采用切割体网格技术划分计算域，网格划分如图2～图4所示。图2为整个流域网格图，自由液面附近网格加密。图3为船体及舵网格划分图，船体首尾及舵网格加密。图4为自由液面网格划分图，船体附近网格加密，以准确捕捉船体周围的流场。

表1 KCS船型主尺度Tab. 1 Principal dimensions of KCS ship types

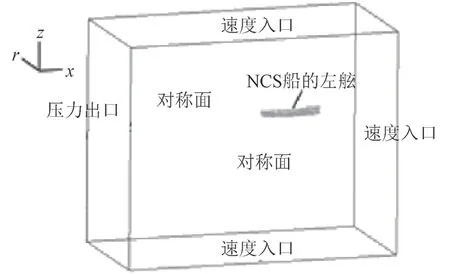
图1 边界条件设置Fig. 1 Boundary conditions

图2 整个计算域网格划分Fig. 2 Mesh on the computational domain

图3 船体及舵表面网格划分Fig. 3 Mesh on the hull and rudder surface

图4 自由液面网格划分Fig. 4 Mesh on the free surface

3 阻力预报流程

以KCS为例，采用RANS法模拟不同航速下船体水动力性能，其中船体分别设置成约束模和自由模，具体计算流程如图5所示。

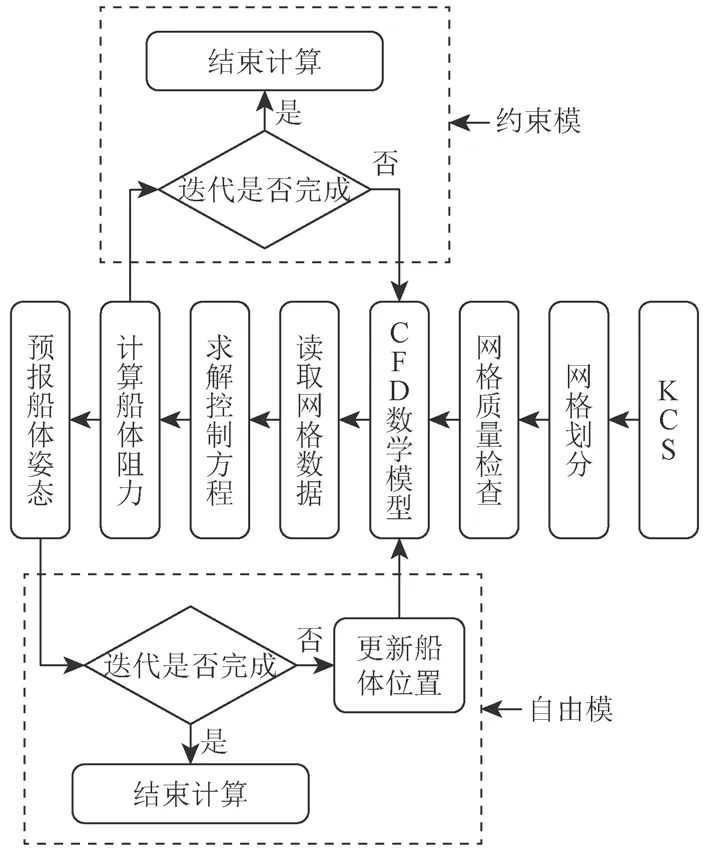
图5 计算流程图Fig. 5 Computational flow chart

4 CFD模型参数影响分析

4.1 边界层对阻力的影响

船体在水中直航时，船体壁面附近会受到流体黏性的影响。对于黏性很小的空气和水来说，黏性对流动的影响仅限于贴近船体表面的一个薄层内，这一薄层以外的黏性影响可以完全忽略。因此，为了准确预报KCS船型阻力，这一层网格的划分显得非常重要。以无因次参数y+表示船体表面第1层网格节点的高度，计算公式为：

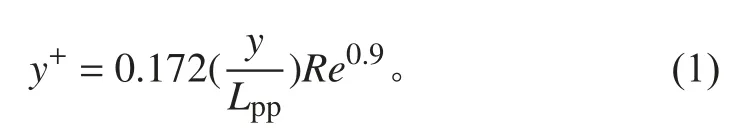
式中：y为第1层网格节点距离船体表面的高度（首层边界层厚度）；Lpp为船体垂线间长；Re为相对船体长度所定义的雷诺数；y+取值范围在30～200。

在边界层网格划分中，首层边界层厚度、网格增长因子和边界层数决定了网格划分方式。因此，按照这3个因子依次讨论边界层划分方式与阻力之间的关系，计算结果如表2～表4所示。

表2 首层边界层厚度与阻力之间的关系Tab. 2 The relation between the thickness of the first boundary layer and the resistance

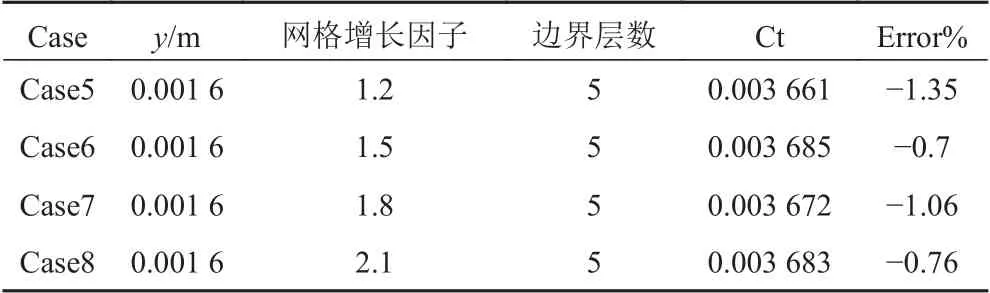
表3 网格增长因子与阻力之间的关系Tab. 3 The relationship between grid growth factor and resistance

表4 边界层数与阻力之间的关系Tab. 4 The relationship between the number ofboundary layers and resistance

从计算结果可以看出，误差变化幅值均低于10%。其中，总阻力随着首层边界层厚度的增加变化明显，而随着网格增长因子和边界层数的增加变化较小。随着首层边界层厚度的增加，船体总阻力增加；随着边界层数的增加，船体总阻力减小；而网格增长因子与船体总阻力之间没有明显的线性关系。从表3可以看出，当网格增长因子为1.5时，计算结果与实验值更接近。

4.2 湍流系数对阻力的影响

根据经验，网格数量的增加会提高阻力预报的准确性。但是随着网格数量的不断增加，计算效率将大大降低，并且网格数量增加到一定程度反而导致计算精度下降。所以在合适的网格数量上探讨高精度的求解方式成为CFD数值模拟的关键。

虽然许多湍流模型已经取得了一定计算效果，但迄今为止仍旧没有得到有效而统一的湍流模型，并且在分析湍流模型方程的一系列参数对计算结果及不确定度的影响这方面，很少有学者进行深入研究。因此，以Realizable k-ε模型作为研究对象，其中该模型的推荐计算值如表5所示。在湍流系数取值范围附近改变取值并分别用来计算船舶阻力，其计算工况及阻力结果如表6～表10所示。

从计算结果可以看出，随着湍流系数的变化，船体总阻力变化范围在2.5%以内。随着Cµ和αk的增加，船体总阻力减小；随着C2ε和αε的增加，船体总阻力增加；而随着C1ε的增加，阻力计算结果没有明显的线性关系。当C1ε＞1.42时，阻力随着C1ε的增加而减小。

表5 Realizable k-ε湍流模型系数Tab. 5 Realizable k-ε turbulence model coefficients

表6 Cµ与阻力之间关系Tab. 6 The relationship between Cµ and resistance

表7 C1ε与阻力之间关系Tab. 7 The relationship between C1ε and resistance

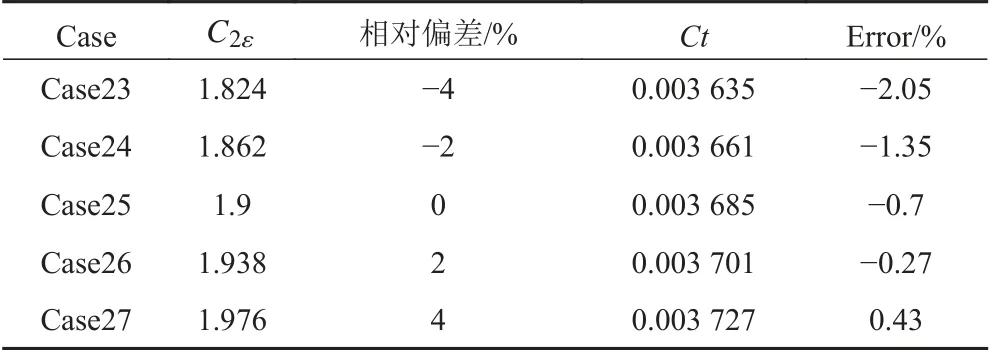
表8 C2ε与阻力之间关系Tab. 8 The relationship between C2ε and resistance

表10 αε与阻力之间关系Tab. 10 The relationship between and resistance

Caseαε 相对偏差/%CtError/%Case330.96-200.003 64-1.91 Case341.08-100.003 665-1.24 Case351.200.003 685-0.7 Case361.32100.003 695-0.43 Case371.44200.003 7230.32

5 模型参数优化及多航速阻力预报

5.1 模型参数优化

为了寻找到更适合KCS船体阻力预报的湍流系数，构建基于NLPQL算法[11]的优化系统。由之前的讨论可以看出，C2ε和αε对阻力的影响较大，而C1ε和αk的变化对阻力影响较小。为了减小设计变量提高优化效率，固定C1ε=1.44，αk=1.0，选取其余3个参数作为优化设计变量。目标函数||RtCFD-RtEFD||为最小值。优化流程图如图6所示，优化过程如图7所示。最优解集如表11所示。可以看出，经过一系列的优化得到了最优湍流系数。按照最优解计算的总阻力与实验值最接近，误差仅有0.054%。

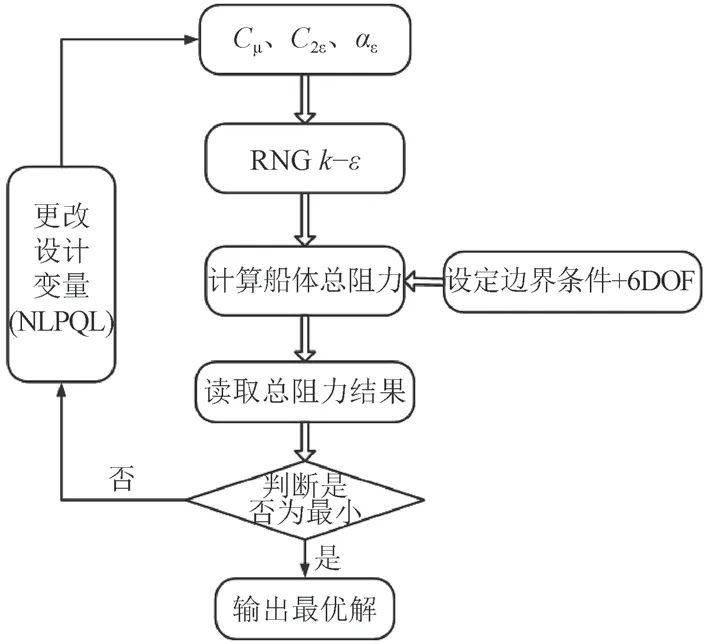
图6 优化流程Fig. 6 Optimization process

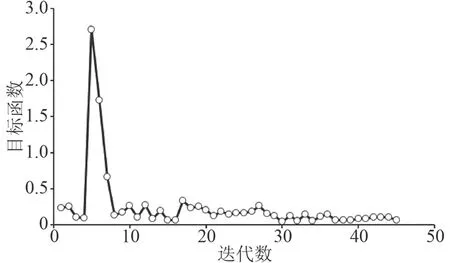
图7 序列二次规划算法优化过程Fig. 7 The optimization process for the NLPQL algorithm

表11 模型系数选取Tab. 11 The selection of Realizable k-ε turbulence model coefficients

5.2 多航速阻力预报

通过以上研究与讨论，明确了船体阻力预报的边界层划分方式和最优湍流系数取值，以下采用该方法预报KCS船在静水中直航的总阻力。

分别根据推荐系数和最优系数对船体总阻力进行预报，表12给出了CFD计算结果与实验值的对比。可以看出，船体设置成自由模型比约束模型计算精度高，平均误差为0.95%。且在高航速时，约束模型误差较大而自由模型阻力预报值与实验值吻合较好，误差只有1.38%。

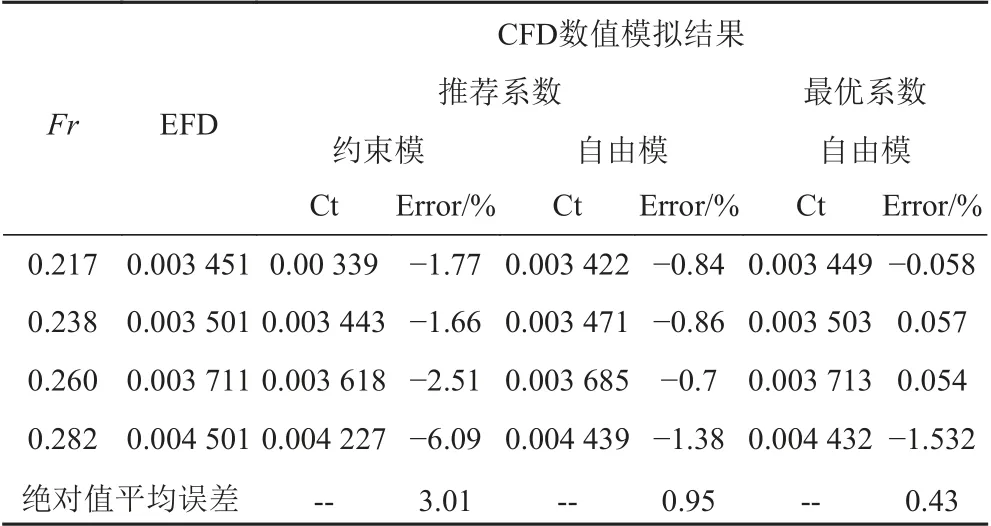
表12 总阻力计算结果与实验值对比Tab. 12 The comparison of the Ct calculated by CFD and EFD methods

图8和图9为船体表面压力分布图。从图中可以发现，在每个航速下，船体表面压力等值线分布变化不大，但在球鼻首部分压力等值线有明显的不同，此处产生的压阻是兴波阻力的主要组成部分。由此可知，只有考虑了船体自身的运动姿态才能更全面的反应船体实际航行特性。在自由模计算中，最优系数在船体总阻力预报上平均误差只有0.43%以内，而推荐系数的阻力计算结果误差在0.95%。可以看出，最优系数在阻力预报精度明显高于推荐系数，只有在Fr=0.282时计算结果较差，以此验证了该湍流系数在多航速船体阻力预报上的实用性与可靠性。

图8 船首表面压力分布（约束模—推荐系数）Fig. 8 Static pressure distribution on the bow section（restraint mode-recommendation coefficients）

图9 船首表面压力分布（自由模—推荐系数）Fig. 9 Static pressure distribution on the bow section（free moderecommended coefficients）

表13给出了船体稳定时刻的纵倾角度和垂荡位移随Fr变化的数值大小。可以看出，本文计算结果与文献[12]中的计算结果较吻合。随着航速的增加，船体升沉明显增大，而纵倾角增加较为缓慢。图10为计算稳定时刻船体航行姿态。

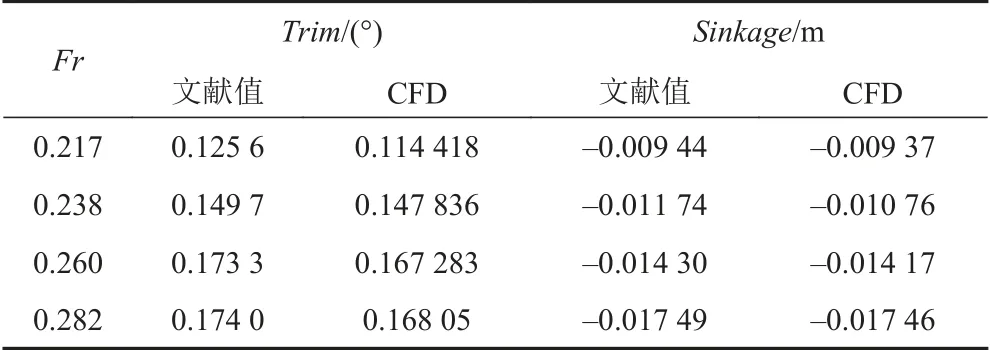
表13 纵倾值和垂荡变化值与文献值对比Tab. 13 The comparison of pitch and heave values obtained by CFD method and previous literature

图10 稳定时刻船体姿态（自由模—最优系数）Fig. 10 Ship attitude at stable time（free mode-optimal coefficients）

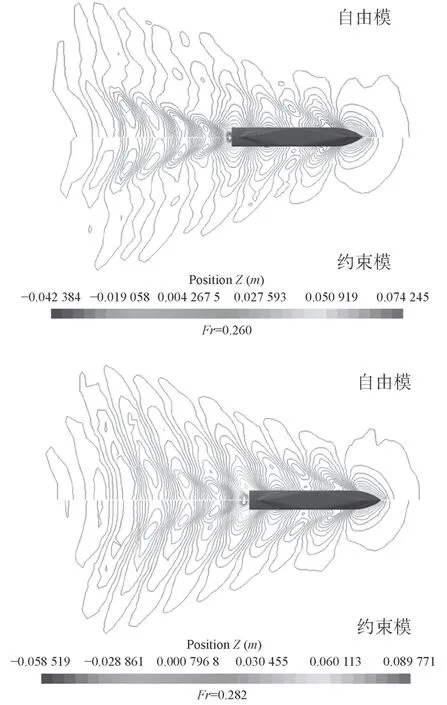
图11 推荐系数波形等高线对比图Fig. 11 The comparison of the waveform contour obtained by recommended coefficients

图11为采用推荐系数计算的自由模与约束模波形等高线对比图。可以看出，2种方法均能较清晰地捕捉到船体周围的波浪形状，说明VOF方法在自由液面捕捉上的优势。虽然2种波形图相似，但是在船首附近的波形相差较大。这主要是由于稳定后自由模在流场中的航行姿态与约束模不同，使得自由模的船体首尾压力差大于约束模。图12为采用自由模计算的KCS船波形等高线对比图。可以看出，在Fr=0.282工况下波形等高线较为相似，而在Fr=0.260时波形等高线差别较大。这与表12中阻力计算结果相符。可见波形等高线的捕捉同样可以作为船体阻力预报正确与否的评价标准之一。

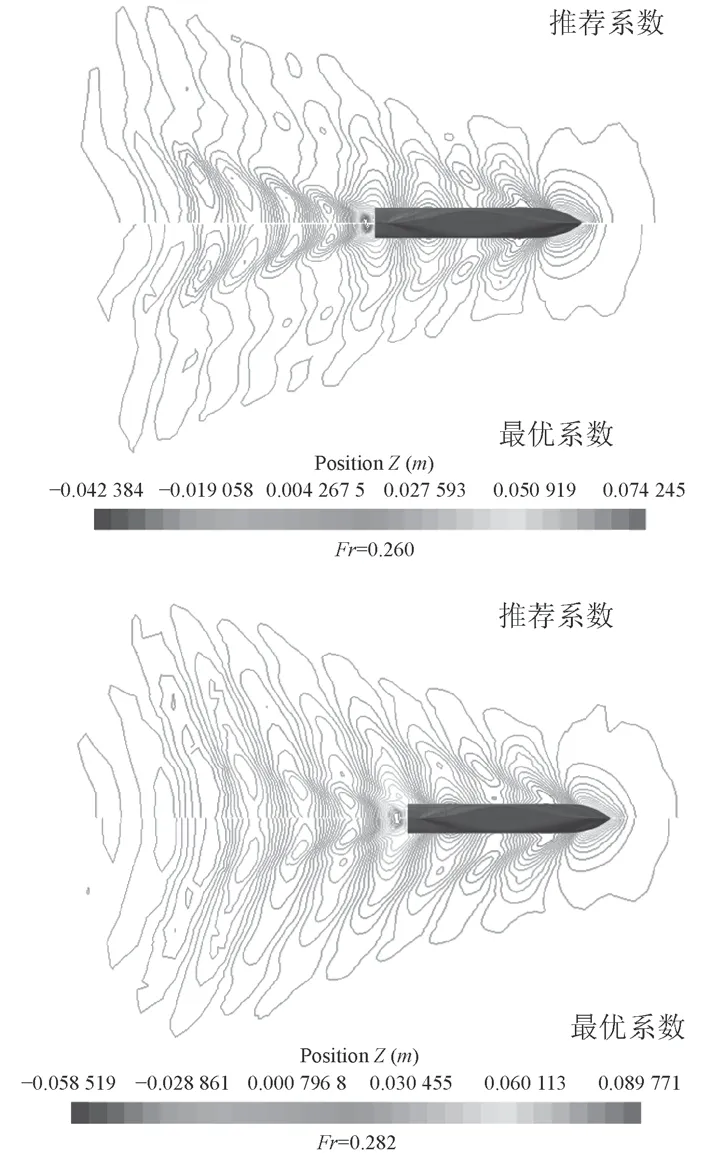
图12 自由模波形等高线对比图Fig. 12 The comparison of the waveform contour obtained by free-mode

6 结 语

本文采用SIMPLE算法求解不可压缩RANS方程，对KCS船在静水中的阻力预报精度进行研究，模拟了不同Fr时KCS船受到的总阻力、船体表面及周围流场分布情况。结果表明：

1）船体附近边界层划分方式对阻力预报有较大的影响。随着首层边界层厚度的增加，阻力也随之增加；随着边界层数的增加，阻力减小；而网格增长因子与阻力之间没有明显的线性关系。

2）C2ε和αε对阻力的影响较大，而C1ε和αk的变化对阻力影响较小。随着Cµ和αk的增加，阻力减小；随着C2ε和αε的增加，阻力增加；而C1ε与阻力之间没有明显的线性关系，但当C1ε＞1.42时，阻力随着C1ε的增加而减小。其次，构建了基于NLPQL法的优化系统，得到了适合KCS船体阻力预报的湍流系数：Cµ=0.09，C1ε=1.44，C2ε=1.950 5，αk=1.0，αε=1.187 5。

3）自由模在船体阻力预报精确度上优于约束模，误差只有0.95%。采用最优湍流系数对船体阻力进行预报时，除了Fr=0.282以外，其他航速阻力计算精确度均高于推荐湍流系数。