立体几何的高考试题交汇题型研究

浙江省安吉县孝丰高级中学 厉伟星

立体几何的学习在高一下半年就会有所涉及，它不仅需要学生拥有较强的空间感，同时还需要拥有良好的想象力。在对立体几何进行学习时，不论是课本上的知识还是试卷上的习题，都是以平面图的方式展现出来的，较强的空间想象力，能够将平面图与立体图相互结合起来，学习起来便会觉得简单许多。立体几何知识的相容性很好，能够与多种知识相互组合，形成新的题型。高考试题中也往往会出现立体几何的交汇题型，这样的题难度较大，可以用来检验学生们对不同知识的掌握情况。

一、立体几何与向量的交汇题型

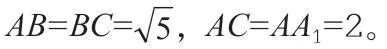
这道题是2018 年的北京高考题，题目中将立体几何的知识与向量相互结合。本题中共分为三个问题，第一问非常简单，需要学生根据已知条件来证明出AC 垂直于平面BEF。第二问则需要学生动一下脑筋，根据题目中的已知内容来构建直角坐标系，根据向量知识来求解余弦值。第三问根据向量进行简单计算，得出二者相交的论点。这道题将立体几何与向量知识相互交汇，学生既要掌握立体几何知识，也需要掌握向量以及角度计算等相关知识，将几方面的知识相互融合，考验学生对于知识的运用能力。

二、立体几何与空间点、直线、平面之间的位置关系的交汇题型

例2：如图2，四边形ABCD 为正方形，E,F 分别为AD,BC 的中点，以DF 为折痕把三角形DFC 折起，使C 到达点P 的位置，且PF 垂直于BF。（1）证明平面PEF 垂直于平面ABFD；（2）求DP 与平面ABFD 所成角的正弦值。

这道题是2018 年高考全国卷一的一道立体几何与空间点、直线、平面之间的位置关系的交汇题型。根据题目所给出的条件，结合相关定理，便能够证明出两者的垂直关系。这道题目的难度不大，只要学生掌握二者垂直的条件和定理，便可以根据题目中所给出的已知条件进行题目的解析。立体几何与空间点、直线、平面之间的位置关系相融合的题型与其他综合类题型相比较为简单，相交、平行、垂直，只要牢牢掌握这三种位置关系的证明定理，结合立体几何的知识，便能够对题目进行解答。

例1 和例2 两种题型虽然是立体几何和向量以及立体几何和空间点、直线、平面之间的位置关系的交汇题型，但是在问题的设置中还涉及其他的知识点，并不完全只是两种知识的相互融合。这类题目在解析过程中除了问题中给出的知识点，还需要进行其他知识的运用。这类题型涉及知识点较多，所以在解题过程中稍显困难，学生需要对几种知识融会贯通，这样才能够顺利进行题目的解答。但凡对其中一种知识的掌握不牢固，在题目的解答上便会遇到困难，这样的题目在高考中难度中等，主要考验学生对于知识的理解和综合运用。

三、立体几何与三角函数的交汇题型

这道题是2017 年北京高考试题，在这道题中，将三角函数与立体几何结合在一起，在立体几何的基础之上加入三角函数的内容，两个问题中没有涉及其他的知识。在这样的题中，学生可以根据所给出的已知条件，结合三角函数的相关知识对题目进行解析。这种题目条件清楚并且问题鲜明，在解析过程中不需要运用太多知识，只根据定理和公式就可以解出答案。这类题目在高考中属于简单题型，将两种知识简单结合，考验学生对于部分知识的掌握情况，学生只需要牢牢记住公式和定理便可以顺利解出题目，拿到分数。

四、立体几何与函数的交汇题型

例4：如图4，动点P 在正方体ABCD-A1B1C1D1的对角线BD1上，过点P 作垂直平面B1BD1D 的直线，与正方体表面相交于M，N。设BP=x，MN=y,则函数y=ƒ(x)的图像大致是？

这道题是2008 年北京高考试题，主要是立体几何与函数的交汇题型。函数的题型变化也非常多，并且难度较大。立体几何与函数的融合，关注的知识点较多，因为函数存在不确定性，有时还需要进行不同种结果分析，这样的题型往往也都是难题。因为立体几何与函数的题型变换很多，学生在掌握基本的立体几何与函数知识后，还需要对知识进行综合运用。在考题的设置中，简单的问题可以几步解出，较难的问题就考验学生对于知识的掌握程度，理解并掌握所有知识点，根据题型类型进行实际分析，才是解决难题的关键所在。

立体几何具有百搭性，与多种知识可以交互融合。在这些问题的解决上，首先就需要对立体几何以及其他知识的基础内容进行有效的理解和掌握。交汇题型的重点就是要考查学生对于不同种知识的相互运用，以上这些交汇的题型都算是一种创新，并且也是高考题型的未来出题趋势。